- Research
- Open access
- Published:
Common fixed point theorems on quasi-cone metric space over a divisible Banach algebra
Advances in Difference Equations volume 2021, Article number: 306 (2021)
Abstract
In this manuscript, we investigate the existence and uniqueness of a common fixed point for the self-mappings defined on quasi-cone metric space over a divisible Banach algebra via an auxiliary mapping ϕ.
1 Introduction and preliminaries
The notion of metric has been extended in several ways by changing the axioms of the metric notion: quasi-metric, symmetric, dislocated metric, b-metric, 2-metric, D-metric, S-metric, G-metric, partial metric, ultra-metric, etc. We shall focus on cone metric space or more precisely, Banach-valued metric space. The idea of Banach-valued metric space was considered by several authors in distinct periods of the last century. This notion became popular and raised interest among researchers after the paper of Huang and X. Zhang [1] in 2007. Since then, a number of authors got the characterization of several known fixed point theorems in the context of Banach-valued metric space, such as, [2–20].
In this paper, we consider common fixed point theorems in the framework of the refined cone metric space, namely, quasi-cone metric space.
In what follows, we shall recall the basic notions and notations as well as the fundamental results.
Definition 1.1
([21])
Suppose \(\mathcal{E}\) is a real Banach algebra, that is, for  , \(a \in \mathrm{R}\),
, \(a \in \mathrm{R}\),
-
(a)
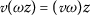 ;
; -
(b)
 ,
,  ;
; -
(c)
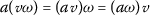 ;
; -
(d)
 .
.
If Banach algebra \(\mathcal{E}\) with unit element e, i.e. multiplicative identity e, is with  for
for  , then \(\| \mathsf{e}\| = 1\).
, then \(\| \mathsf{e}\| = 1\).
An element  is said to be invertible if there exists
is said to be invertible if there exists  such that
such that  . Moreover, if every non-zero element of \(\mathcal{E}\) has an inverse in \(\mathcal{E}\), then \(\mathcal{E}\) is called a divisible Banach algebra.
. Moreover, if every non-zero element of \(\mathcal{E}\) has an inverse in \(\mathcal{E}\), then \(\mathcal{E}\) is called a divisible Banach algebra.
Proposition 1.2
([22])
Let \(\mathcal{E}\) be a Banach algebra,  an element in \(\mathcal{E}\) and
an element in \(\mathcal{E}\) and  the spectral radius of
the spectral radius of  . If
. If  then
then  is invertible in \(\mathcal{E}\) and
is invertible in \(\mathcal{E}\) and

Remark 1.3
([2])
 for all
for all  in a Banach algebra \(\mathcal{E}\).
in a Banach algebra \(\mathcal{E}\).
Let \((\mathcal{E}, \|\cdot \|)\) be a real algebra and P a closed subset of \(\mathcal{E}\).
The set P is a cone if the following conditions hold:
- \((c_{1})\):
-
P is non-empty and \(\mathsf{P}\neq \{ \theta \} \);
- \((c_{2})\):
-
 for all
for all  and \(\mathsf{a}_{1},\mathsf{a}_{2}\in (0,\infty )\);
and \(\mathsf{a}_{1},\mathsf{a}_{2}\in (0,\infty )\); - \((c_{3})\):
-
\(\mathsf{P}\cap (-\mathsf{P})= \{ \theta \} \).
Moreover, for a given cone \(\mathsf{P}\subseteq \mathcal{E}\) we can consider a partial ordering ≤ such that  if and only if
if and only if  . We write
. We write  for
for  and
and  indicates that
indicates that  and
and  . The cone P is called normal if there exists a constant \(N > 0\) such that
. The cone P is called normal if there exists a constant \(N > 0\) such that  implies
implies  , for
, for  and is called solid if \(\textit{intP} \neq \emptyset \).
and is called solid if \(\textit{intP} \neq \emptyset \).
Definition 1.4
([3])
Let  be a sequence in a solid cone P. We say that
be a sequence in a solid cone P. We say that  is a
is a  -sequence, if for any
-sequence, if for any  with
with  there exists \(m_{0}\in \mathbb{N}\) such that
there exists \(m_{0}\in \mathbb{N}\) such that  for all \(m>m_{0}\).
for all \(m>m_{0}\).
Lemma 1.5
([3])
If  is a
is a  -sequence in a solid cone P and κ is arbitrary (but given) in P, then
-sequence in a solid cone P and κ is arbitrary (but given) in P, then  is also a
is also a  -sequence.
-sequence.
Lemma 1.6
([4])
On a real Banach algebra \(\mathcal{E}\) with a solid cone \(\mathcal{E}\), the following statements hold:
-
1
\(\varsigma \ll \omega \) if
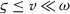 ;
; -
2
\(\varsigma =\theta \) if \(\varsigma \ll \omega \) for every \(\omega \gg \theta \).
Let \(\mathcal{E}\) be a Banach algebra and \(\mathsf{P}\subset \mathcal{E}\) be a cone. Then  is an invertible element in P for any
is an invertible element in P for any  with
with  .
.
Definition 1.7
([23])
Suppose \(\mathcal{E}\) is a Banach algebra with unit e and \(\mathsf{P}\subseteq \mathcal{E}\) is a cone. P is called algebra cone if \(\mathsf{e}\in \mathsf{P}\) and for  ,
,  .
.
In what follows we consider that \(\mathcal{E}\) (\(\mathcal{E}_{d}\)) represents a real (divisible) Banach algebra with a unit e and θ be its zero element, P is a solid cone in \(\mathcal{E}\), \(\mathsf{P}_{\mathcal{E}_{d}}\) a normal algebra cone in \(\mathcal{E}_{d}\) with a normal constant N and X is a non-empty set.
Definition 1.8
(see [24])
A mapping \(\mathsf{d}: \mathrm{X}\times \mathrm{X}\rightarrow \mathcal{E}\) is a cone metric on X if
-
(a)
 for all
for all  and
and 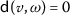 if and only if
if and only if  ,
, -
(b)
 for all
for all  ,
, -
(c)
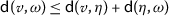 ,
,
for all  . The pair \((\mathrm{X}, \mathsf{d})\) is said to be a cone metric space over Banach algebra, in short, CMS.
. The pair \((\mathrm{X}, \mathsf{d})\) is said to be a cone metric space over Banach algebra, in short, CMS.
Definition 1.9
(see [25])
A mapping \(\mathsf{q}: \mathrm{X}\times \mathrm{X}\rightarrow \mathcal{E}\) is said to be a quasi-cone metric if
-
(a)
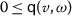 for all
for all  ,
, -
(b)
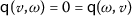 if and only if
if and only if  ,
, -
(c)
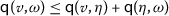 ,
,
for all  . The triplet \((\mathrm{X}, \mathsf{q}, \mathcal{E})\) is said to be a quasi-cone metric space over Banach algebra, in short, qCMS.
. The triplet \((\mathrm{X}, \mathsf{q}, \mathcal{E})\) is said to be a quasi-cone metric space over Banach algebra, in short, qCMS.
A quasi-cone metric space is called Δ-symmetric, if there exists an invertible element \(\Delta \in \mathcal{E}\) such that

for all  .
.
Definition 1.10
Suppose \((\mathrm{X}, \mathsf{q}, \mathcal{E})\) is a qCMS,  and
and  is a sequence in X. Then
is a sequence in X. Then
-
(a)
 (bi)-converges to
(bi)-converges to  if for \(c\in \mathcal{E}\) with \(\theta \ll c\), there is a natural number N satisfying
if for \(c\in \mathcal{E}\) with \(\theta \ll c\), there is a natural number N satisfying 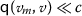 and
and  for \(m\geq N\). We denote
for \(m\geq N\). We denote 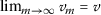 or
or  .
. -
(b)
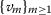 is a (l)(left)-Cauchy ((r)(right)-Cauchy)) if for \(c\in \mathcal{E}\) with \(\theta \ll c\), there exists a natural number N satisfying
is a (l)(left)-Cauchy ((r)(right)-Cauchy)) if for \(c\in \mathcal{E}\) with \(\theta \ll c\), there exists a natural number N satisfying  (respectively,
(respectively, 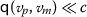 for \(m>p \geq N\).
for \(m>p \geq N\). -
(c)
 is a bi-Cauchy if for \(c\in \mathcal{E}\) with \(\theta \ll c\), there exists a natural number N satisfying
is a bi-Cauchy if for \(c\in \mathcal{E}\) with \(\theta \ll c\), there exists a natural number N satisfying 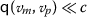 for \(m,p \geq N\).
for \(m,p \geq N\). -
(d)
\((\mathrm{X}, \mathsf{q}, \mathcal{E})\) is (l)-complete ((r)-complete) if every (l)-Cauchy((r)-Cauchy) sequence is (bi)-convergent and is complete if it is (l) and (r)-complete.
Definition 1.11
We say that the mapping \(\psi : \mathsf{P}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}_{ \mathcal{E}_{d}}\) is a ψ-operator if
-
(a)
ψ is an increasing;
-
(b)
ψ is a continuous bijection and has an inverse mapping \(\psi ^{-1} \) which is also continuous and increasing;
-
(c)
 for all
for all  ;
; -
(d)
 for all
for all  .
.
Remark 1.12
By Definition 1.11, the part of (c), we can obtain  for all
for all  . In fact, note that
. In fact, note that  for all
for all  and \(\psi ^{-1}\) is also a continuous and increasing operator, then
and \(\psi ^{-1}\) is also a continuous and increasing operator, then

which yields

Hence,

Since \(\psi : \mathsf{P}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}_{ \mathcal{E}_{d}}\) is a continuous bijection, thus  , for all
, for all  .
.
Remark 1.13
By Definition 1.11, the part of (d), we can obtain  , for
, for  .
.
Indeed, from  for
for  and \(\psi ^{-1} : \mathsf{P}_{\mathcal{E}}\rightarrow \mathsf{P}_{\mathcal{E}}\) is also continuous, we get
and \(\psi ^{-1} : \mathsf{P}_{\mathcal{E}}\rightarrow \mathsf{P}_{\mathcal{E}}\) is also continuous, we get

which yields

Then we obtain

Thanks to that \(\psi : \mathsf{P}_{\mathcal{E}}\rightarrow \mathsf{P}_{\mathcal{E}}\) is a continuous bijection,  , for all
, for all  .
.
Remark 1.14
For example, let \(E_{d}=\mathrm{R}\) be a divisible Banach algebra,  be a normal cone in \(\mathcal{E}_{d}\), suppose \(\psi : \mathsf{P}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}_{ \mathcal{E}_{d}}\), defined by
be a normal cone in \(\mathcal{E}_{d}\), suppose \(\psi : \mathsf{P}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}_{ \mathcal{E}_{d}}\), defined by  and then
and then  , for all
, for all  .
.
2 Main results
Lemma 2.1
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a Δ-symmetric qCMS over a divisible Banach algebra,  a sequence in X. If there exists \(\kappa \in \mathsf{P}_{\mathcal{E}_{d}}\), with \(\rho (\kappa )<1\) such that
a sequence in X. If there exists \(\kappa \in \mathsf{P}_{\mathcal{E}_{d}}\), with \(\rho (\kappa )<1\) such that

for all \(m\in \mathbb{N}\), then  is a (bi)-Cauchy sequence.
is a (bi)-Cauchy sequence.
Proof
First of all, we remark that, successively applying Eq. (2), we have

Let \(m>p \geq N\). Thereupon,

Now, since \(\rho (\kappa )<1\), and taking into account Proposition 1.2, we see that \((\mathsf{e}-\kappa )\) is an invertible element and \((\mathsf{e}-\kappa )^{-1}=\sum_{j=0}^{\infty }\kappa ^{j}\) and the above inequality becomes

For a given  , with
, with  , we choose \(\delta >0\) such that
, we choose \(\delta >0\) such that  . (Here \(N_{\delta }(\theta )= \{ \omega \in \mathcal{E}_{d}:\|\omega \|\}< \delta \} \).) Letting \(p_{0}\in \mathbb{N}\) such that
. (Here \(N_{\delta }(\theta )= \{ \omega \in \mathcal{E}_{d}:\|\omega \|\}< \delta \} \).) Letting \(p_{0}\in \mathbb{N}\) such that  for all \(p\geq p_{0}\) we get
for all \(p\geq p_{0}\) we get  , for all \(p\geq p_{0}\). Therefore,
, for all \(p\geq p_{0}\). Therefore,

Then by (b) in Definition 1.10 it follows that the sequence  is (l)-Cauchy. On the other hand, from Definition 1.4, we see that the sequence
is (l)-Cauchy. On the other hand, from Definition 1.4, we see that the sequence  is
is  -convergent and moreover in view of Lemma 1.5 the sequence
-convergent and moreover in view of Lemma 1.5 the sequence  , where \(\Delta \in \mathsf{P}_{\mathcal{E}_{d}}\), is also a
, where \(\Delta \in \mathsf{P}_{\mathcal{E}_{d}}\), is also a  -sequence, that is,
-sequence, that is,

for all \(m>p>p_{0}\). But, since the space \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) is supposed to be Δ-symmetric, we have

and taking Lemma 1.5 into account we get  , for all \(m>p\geq p_{0}\), which means the sequence
, for all \(m>p\geq p_{0}\), which means the sequence  is (r)-Cauchy. Obviously, in view of statement \((c)\) in Definition 1.10, it follows that
is (r)-Cauchy. Obviously, in view of statement \((c)\) in Definition 1.10, it follows that  is a (bi)-Cauchy sequence. □
is a (bi)-Cauchy sequence. □
Let (\(\mathcal{E}_{d}\)) be a real (divisible) Banach algebra with a unit e and θ be its zero element and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\) be a normal algebra cone with constant \(N=1\) in \(\mathcal{E}_{d}\).
Theorem 2.2
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a complete Δ-symmetric qCMS over \(\mathcal{E}_{d}\) and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Suppose that \(\psi : \mathsf{P}^{1}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}^{1}_{ \mathcal{E}_{d}}\) is a ψ-operator and \(\mathcal{U}, \mathcal{V}: \mathrm{X}\rightarrow \mathrm{X}\) are mappings satisfying the conditions


for all  with
with  , where \(\psi (e) \leq k < \psi (2e)\) in \(\mathsf{P}_{\mathcal{E}^{1}_{d}}\). Then \(\mathcal{U}\) and \(\mathcal{V}\) have a common fixed point.
, where \(\psi (e) \leq k < \psi (2e)\) in \(\mathsf{P}_{\mathcal{E}^{1}_{d}}\). Then \(\mathcal{U}\) and \(\mathcal{V}\) have a common fixed point.
Proof
Let  be an arbitrary point and the sequence
be an arbitrary point and the sequence  defined by
defined by

Then, setting  and
and  , we get
, we get

and then

Also if we put  and
and  , then we have
, then we have

Thus,

Moreover, applying \(\psi ^{-1}\) in (8), (9) and keeping in mind the properties of the operator \(\psi ^{-1}\), it follows

or by simplifying, we obtain

Denoting \(\kappa =\psi ^{-1}(k)-\mathsf{e}\), the above inequalities pass into

for any positive integer m. Now, by hypothesis \(\psi (\mathsf{e})\leq k<\psi (2\mathsf{e})\) it follows that \(\theta \leq \psi ^{-1}(k)-\mathsf{e}<\mathsf{e}\) and since the cone \(\mathsf{P}_{\mathcal{E}_{d}}\) is normal (with \(N=1\)),
and then \(\rho (\kappa )<1\). Thereupon, by Lemma 2.1 we see that the sequence  is (bi)-Cauchy. Further, we can find
is (bi)-Cauchy. Further, we can find  such that the sequence
such that the sequence  converges to
converges to  . That is, for every
. That is, for every  there exists \(m_{1}\in \mathbb{N}\) such that
there exists \(m_{1}\in \mathbb{N}\) such that  and
and  , for \(m\geq m_{1}\). Thus, replacing in (5)
, for \(m\geq m_{1}\). Thus, replacing in (5)  by
by  and ω by
and ω by  we have
we have

and from (c), Definition 1.11,

Moreover, by Definition 1.9 and Remark 1.13, we have

and from Lemma 1.6 we obtain  . Therefore,
. Therefore,  . Similarly, choosing in (6)
. Similarly, choosing in (6)  and
and  , and taking into account the properties of ψ we have
, and taking into account the properties of ψ we have

which leads us to

Consequently,  . □
. □
Example 2.3
Let \(\mathcal{E}_{d}=\mathbb{R}^{2}\),  and for any
and for any  we define the multiplication as
we define the multiplication as  . Then \(\mathcal{E}_{d}\) is a Banach algebra with a unit \(\mathsf{e}=(1,1)\). Let \(\mathrm{X}= \{ 1,3,4,5 \} \) and \(\mathsf{q}:\mathrm{X}\times \mathrm{X}\rightarrow \mathcal{E}\) defined by
. Then \(\mathcal{E}_{d}\) is a Banach algebra with a unit \(\mathsf{e}=(1,1)\). Let \(\mathrm{X}= \{ 1,3,4,5 \} \) and \(\mathsf{q}:\mathrm{X}\times \mathrm{X}\rightarrow \mathcal{E}\) defined by

be a 2-symmetric quasi-metric on X. Consider also the mappings \(\mathcal{U},\mathcal{V}:\mathrm{X}\rightarrow \mathrm{X}\) defined by \(\mathcal{U}1=1\), \(\mathcal{U}3=3\), \(\mathcal{U}4=3\), \(\mathcal{U}5=5\) and \(\mathcal{V}1=1\), \(\mathcal{V}3=3\), \(\mathcal{V}4=4\), \(\mathcal{V}5=4\). Then we have
Let \(\psi :\mathsf{P}^{1}{\mathcal{E}}\rightarrow \mathsf{P}^{1}{ \mathcal{E}}\),  and \(k=(\frac{9}{8},\frac{9}{8})\).
and \(k=(\frac{9}{8},\frac{9}{8})\).
Therefore:
-
1
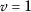 , \(\omega =3\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(1,\mathcal{U}1)\bigr)+\psi \bigl(\mathsf{q}(3, \mathcal{V}3)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(1,3)\bigr), \\& \psi \bigl(\mathsf{q}(1,\mathcal{V}1)\bigr)+\psi \bigl(\mathsf{q}(3, \mathcal{U}3)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(1,3)\bigr) \end{aligned}$$
, \(\omega =3\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(1,\mathcal{U}1)\bigr)+\psi \bigl(\mathsf{q}(3, \mathcal{V}3)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(1,3)\bigr), \\& \psi \bigl(\mathsf{q}(1,\mathcal{V}1)\bigr)+\psi \bigl(\mathsf{q}(3, \mathcal{U}3)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(1,3)\bigr) \end{aligned}$$ -
2
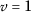 , \(\omega =4\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(1,\mathcal{U}1)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{V}4)\bigr)=(0,0) \leq \biggl(\frac{27}{4},\frac{27}{8} \biggr)=k\psi \bigl(\mathsf{q}(1,4)\bigr) , \\& \psi \bigl(\mathsf{q}(1,\mathcal{V}1)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{U}4)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl( \frac{27}{4},\frac{27}{8}\biggr)=k\psi \bigl(\mathsf{q}(1,4) \bigr) \end{aligned}$$
, \(\omega =4\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(1,\mathcal{U}1)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{V}4)\bigr)=(0,0) \leq \biggl(\frac{27}{4},\frac{27}{8} \biggr)=k\psi \bigl(\mathsf{q}(1,4)\bigr) , \\& \psi \bigl(\mathsf{q}(1,\mathcal{V}1)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{U}4)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl( \frac{27}{4},\frac{27}{8}\biggr)=k\psi \bigl(\mathsf{q}(1,4) \bigr) \end{aligned}$$ -
3
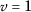 , \(\omega =5\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(1,\mathcal{U}1)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{V}5)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl(9, \frac{9}{2}\biggr)=k\psi \bigl(\mathsf{q}(1,5)\bigr), \\& \psi \bigl(\mathsf{q}(1,\mathcal{V}1)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{U}5)\bigr)=(0,0) \leq \biggl(9,\frac{9}{2}\biggr)=k\psi \bigl( \mathsf{q}(1,5)\bigr) \end{aligned}$$
, \(\omega =5\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(1,\mathcal{U}1)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{V}5)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl(9, \frac{9}{2}\biggr)=k\psi \bigl(\mathsf{q}(1,5)\bigr), \\& \psi \bigl(\mathsf{q}(1,\mathcal{V}1)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{U}5)\bigr)=(0,0) \leq \biggl(9,\frac{9}{2}\biggr)=k\psi \bigl( \mathsf{q}(1,5)\bigr) \end{aligned}$$ -
4
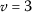 , \(\omega =4\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(3,\mathcal{U}3)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{V}4)\bigr)=(0,0) \leq \biggl(\frac{9}{4},\frac{9}{8} \biggr)=k\psi \bigl(\mathsf{q}(3,4)\bigr), \\& \psi \bigl(\mathsf{q}(3,\mathcal{V}3)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{U}4)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl( \frac{9}{4},\frac{9}{8}\biggr)=k\psi \bigl(\mathsf{q}(3,4) \bigr) \end{aligned}$$
, \(\omega =4\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(3,\mathcal{U}3)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{V}4)\bigr)=(0,0) \leq \biggl(\frac{9}{4},\frac{9}{8} \biggr)=k\psi \bigl(\mathsf{q}(3,4)\bigr), \\& \psi \bigl(\mathsf{q}(3,\mathcal{V}3)\bigr)+\psi \bigl(\mathsf{q}(4, \mathcal{U}4)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl( \frac{9}{4},\frac{9}{8}\biggr)=k\psi \bigl(\mathsf{q}(3,4) \bigr) \end{aligned}$$ -
5
 , \(\omega =5\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(3,\mathcal{U}3)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{V}5)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl( \frac{9}{2},\frac{9}{4}\biggr)=k\psi \bigl(\mathsf{q}(3,5) \bigr), \\& \psi \bigl(\mathsf{q}(3,\mathcal{V}3)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{U}5)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(3,5)\bigr) \end{aligned}$$
, \(\omega =5\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(3,\mathcal{U}3)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{V}5)\bigr)=\biggl(1, \frac{1}{2}\biggr)\leq \biggl( \frac{9}{2},\frac{9}{4}\biggr)=k\psi \bigl(\mathsf{q}(3,5) \bigr), \\& \psi \bigl(\mathsf{q}(3,\mathcal{V}3)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{U}5)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(3,5)\bigr) \end{aligned}$$ -
6
 , \(\omega =5\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(4,\mathcal{U}4)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{V}5)\bigr)=(2,1) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(3,5)\bigr), \\& \psi \bigl(\mathsf{q}(4,\mathcal{V}4)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{U}5)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(3,5)\bigr). \end{aligned}$$
, \(\omega =5\) $$\begin{aligned}& \psi \bigl(\mathsf{q}(4,\mathcal{U}4)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{V}5)\bigr)=(2,1) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(3,5)\bigr), \\& \psi \bigl(\mathsf{q}(4,\mathcal{V}4)\bigr)+\psi \bigl(\mathsf{q}(5, \mathcal{U}5)\bigr)=(0,0) \leq \biggl(\frac{9}{2},\frac{9}{4} \biggr)=k\psi \bigl(\mathsf{q}(3,5)\bigr). \end{aligned}$$
Consequently, the assumptions of Theorem 2.2 are verified and the mappings \(\mathcal{U}\), \(\mathcal{V}\) have 2 common fixed points, these being  ,
,  .
.
Corollary 2.4
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a complete Δ-symmetric qCMS over \(\mathcal{E}_{d}\) and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Suppose that \(\psi : \mathsf{P}^{1}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}^{1}_{ \mathcal{E}_{d}}\) is a ψ-operator and \(\mathcal{U}: \mathrm{X}\rightarrow \mathrm{X}\) is a mapping satisfying the condition

for all  with
with  , where \(\psi (e) \leq k < \psi (2e)\) in \(\mathsf{P}_{\mathcal{E}^{1}_{d}}\). Then \(\mathcal{U}\) has a fixed point.
, where \(\psi (e) \leq k < \psi (2e)\) in \(\mathsf{P}_{\mathcal{E}^{1}_{d}}\). Then \(\mathcal{U}\) has a fixed point.
Proof
Put \(\mathcal{U}=\mathcal{V}\) in Theorem 2.2. □
Theorem 2.5
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a complete Δ-symmetric qCMS over \(\mathcal{E}_{d}\) and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Suppose that \(\psi : \mathsf{P}^{1}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}^{1}_{ \mathcal{E}_{d}}\) is a ψ-operator and \(\mathcal{U}, \mathcal{V}: \mathrm{X}\rightarrow \mathrm{X}\) are mappings satisfying the conditions


for all  with
with  , where
, where
in \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Then \(\mathcal{U}\) and \(\mathcal{V}\) have a common fixed point. Moreover, if \(\psi ^{-1}(\beta )<\psi ^{-1}(\alpha _{1})\) then the common fixed point is unique.
Proof
Let  be the sequence in X defined by (7). Letting
be the sequence in X defined by (7). Letting  and
and  in (11) we have
in (11) we have

or

Taking into account the properties of \(\psi ^{-1}\), we have

and moreover

Therefore, since the Banach algebra is divisible, we get

If we denote \(\kappa =(\psi ^{-1}(\alpha _{1})+\psi ^{-1}(\alpha _{3}))^{-1}(\psi ^{-1}( \beta )-\psi ^{-1}(\alpha _{2}))\), we can easily see that \(\theta \leq \kappa <\mathsf{e}\) and

In the same way, for  and
and  , (12) becomes
, (12) becomes

or, equivalent

Thereupon,

which yields

(here we took into account that the Banach algebra is divisible). Now, by (13) and (14) we have

for all \(m\in \mathbb{N}\), where \(\theta \leq \kappa <\mathsf{e}\). Then, by using Lemma 2.1, we see that the sequence  is (bi)-Cauchy and since the qCMS \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) is complete, we can have
is (bi)-Cauchy and since the qCMS \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) is complete, we can have  such that
such that  converges to
converges to  . Thus, there exists \(m_{2}\in \mathbb{N}\) such that for any
. Thus, there exists \(m_{2}\in \mathbb{N}\) such that for any  we have
we have  ,
,  and also
and also  ,
,  , for any \(m\geq m_{1}\). Hence, by (11), respectively, (12) we have
, for any \(m\geq m_{1}\). Hence, by (11), respectively, (12) we have

for \(m\geq m_{2}\). Moreover, applying \(\psi ^{-1}\) in the above inequalities,

which are equivalent (since the Banach algebra is divisible) with

for all \(m\geq m_{2}\) and any  . Therefore, by Lemma 1.6, it follows that
. Therefore, by Lemma 1.6, it follows that  and also
and also  , which means that
, which means that  is a common fixed point of the mappings \(\mathcal{V}\), \(\mathcal{U}\).
is a common fixed point of the mappings \(\mathcal{V}\), \(\mathcal{U}\).
Finally, considering the additional hypothesis, we will prove the uniqueness of the common fixed point. Supposing, on the contrary, that there exists another point, let us say \(\omega _{*}\in \mathrm{X}\) different from  , such that
, such that  , we have, by (11), for example,
, we have, by (11), for example,

Thus,

and we obtain

for any \(n\in \mathbb{N}\). Further, since \((\psi ^{-1}(\alpha _{1}))^{-1}\psi ^{-1}(\beta )<\mathsf{e}\), we get
as \(n\rightarrow \infty \), which means that for any  we can have \(n_{0}\in \mathbb{N}\) such that
we can have \(n_{0}\in \mathbb{N}\) such that

Thereby, by Lemma 1.6 it follows that  , and
, and  is the unique fixed point of the mappings \(\mathcal{U}\) and \(\mathcal{V}\). □
is the unique fixed point of the mappings \(\mathcal{U}\) and \(\mathcal{V}\). □
Corollary 2.6
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a complete Δ-symmetric qCMS over \(\mathcal{E}_{d}\) and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Suppose that \(\psi : \mathsf{P}^{1}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}^{1}_{ \mathcal{E}_{d}}\) is a ψ-operator and \(\mathcal{U}: \mathrm{X}\rightarrow \mathrm{X}\) is a mapping satisfying the condition

for all  with
with  , where
, where
in \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Then \(\mathcal{U}\) has a fixed point. Moreover, if \(\psi ^{-1}(\beta )<\psi ^{-1}(\alpha _{1})\) then the fixed point is unique.
Proof
Put \(\mathcal{U}=\mathcal{V}\) in Theorem 2.5. □
Theorem 2.7
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a complete Δ-symmetric qCMS over \(\mathcal{E}_{d}\) and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\) be a normal algebra cone in \(\mathcal{E}_{d}\). Suppose that \(\psi : \mathsf{P}^{1}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}^{1}_{ \mathcal{E}_{d}}\) is a ψ-operator and \(\mathcal{U}, \mathcal{V}: \mathrm{X}\rightarrow \mathrm{X}\) are mappings satisfying the conditions


for all  with
with  , where \(\theta \leq \psi ^{-1}(\beta )+(\Delta -\mathsf{e})\psi ^{-1}( \alpha _{3})\leq \psi ^{-1}(\alpha _{1}) \) in \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Then \(\mathcal{U}\) and \(\mathcal{V}\) have a common fixed point.
, where \(\theta \leq \psi ^{-1}(\beta )+(\Delta -\mathsf{e})\psi ^{-1}( \alpha _{3})\leq \psi ^{-1}(\alpha _{1}) \) in \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Then \(\mathcal{U}\) and \(\mathcal{V}\) have a common fixed point.
Proof
Let  be the sequence in X defined by (7). Letting
be the sequence in X defined by (7). Letting  and
and  , by (16), we have
, by (16), we have

Moreover, by applying \(\psi ^{-1}\), and taking into account the properties of it,

and using the triangle inequality we get

and then

which is equivalent with

Further, since the qCMS is Δ-symmetric, there exists an invertible element \(\Delta \in \mathcal{E}\) such that  , for all \(m\in \mathbb{N}\) and then we have
, for all \(m\in \mathbb{N}\) and then we have

Therefore,

On the other hand, with  and
and  , the inequality (17) becomes
, the inequality (17) becomes

Applying \(\psi ^{-1}\) and keeping in mind its properties we get

Therefore, since

we have

Thus,

and

Consequently, from (18) we conclude that

for any \(m\in \mathbb{N}\), where \(\kappa =(\psi ^{-1}(\alpha _{1})+\psi ^{-1}(\alpha _{3}))^{-1}(\psi ^{-1}( \beta )+\Delta \psi ^{-1}(\alpha _{3}))<\mathsf{e}\). In this case we get \(\rho (\kappa )<1\) and taking into account Lemma 2.1 we can conclude that the sequence  is Cauchy and moreover convergent to an element
is Cauchy and moreover convergent to an element  . Therefore, for any
. Therefore, for any  , there exists \(m_{1}\in \mathbb{N}\) such that
, there exists \(m_{1}\in \mathbb{N}\) such that  ,
,  . We claim that
. We claim that  is a fixed point of mappings \(\mathcal{V}\) and \(\mathcal{U}\). Indeed, from (16) and (17) we have
is a fixed point of mappings \(\mathcal{V}\) and \(\mathcal{U}\). Indeed, from (16) and (17) we have

which becomes (by applying \(\psi ^{-1}\))

But since  and also
and also

we get

Thereupon,

which (by taking into account Lemma 1.6) shows us that  .
.
Now, similarly, by (19), we have

which is equivalent with

Moreover, by using the triangle inequality,

then

Thus,  and
and  is a common fixed point of the mappings \(\mathcal{V}\) and \(\mathcal{U}\). □
is a common fixed point of the mappings \(\mathcal{V}\) and \(\mathcal{U}\). □
Corollary 2.8
Let \((\mathrm{X}, \mathsf{q}, \mathcal{E}_{d})\) be a complete Δ-symmetric qCMS over \(\mathcal{E}_{d}\) and \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\) be a normal algebra cone in \(\mathcal{E}_{d}\). Assume \(\psi : \mathsf{P}^{1}_{\mathcal{E}_{d}} \rightarrow \mathsf{P}^{1}_{ \mathcal{E}_{d}}\) is a ψ-operator and \(\mathcal{U}: \mathrm{X}\rightarrow \mathrm{X}\) is satisfying the condition

for all  with
with  , where \(\theta \leq \psi ^{-1}(\beta )+(\Delta -\mathsf{e})\psi ^{-1}( \alpha _{3})\leq \psi ^{-1}(\alpha _{1}) \) in \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Then \(\mathcal{U}\) has a fixed point.
, where \(\theta \leq \psi ^{-1}(\beta )+(\Delta -\mathsf{e})\psi ^{-1}( \alpha _{3})\leq \psi ^{-1}(\alpha _{1}) \) in \(\mathsf{P}^{1}_{\mathcal{E}_{d}}\). Then \(\mathcal{U}\) has a fixed point.
Availability of data and materials
The data and material used to support the findings of this study are included within the article.
References
Huang, L.-G., Zhang, X.: Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 332(2), 1468–1476 (2007)
Cho, S.-H.: Fixed point theorems in complete cone metric spaces over Banach algebras. J. Funct. Spaces 2018, Article ID 9395057 (2018)
Huang, H.-P., Radenović, S.: Some fixed point results of generalized Lipschitz mappings on cone b-metric spaces over Banach algebras. J. Comput. Anal. Appl. 20, 566–583 (2016)
Janković, S., Kadelburg, Z., Radenović, S.: On cone metric spaces: a survey. Nonlinear Anal., Theory Methods Appl. 4(7), 2591–2601 (2011)
Abdeljawad, T., Turkoglu, D., Abuloha, M.: Some theorems and examples of cone Banach spaces. J. Comput. Anal. Appl. 12(4), 739–753 (2010)
Afshari, H., Alsulami, H.H., Karapinar, E.: On the extended multivalued Geraghty type contractions. J. Nonlinear Sci. Appl. 9, 4695–4706 (2016). https://doi.org/10.22436/jnsa.009.06.108
Afshari, H., Rezapour, Sh., Shahzad, N.: Absolute retractivity of the common fixed points set of two multifunctions. Topol. Methods Nonlinear Anal. 40, 429–436 (2012)
Karapınar, E., Tukoglu, A.D.: Best approximations theorem for a couple in cone Banach space. Fixed Point Theory Appl. 2010, Article ID 784578 (2010)
Abdeljawad, T., Karapınar, E., Taş, K.: Common fixed point theorems in cone Banach spaces. Hacet. J. Math. Stat. 40(2), 211–217 (2011)
Abdeljawad, T., Karapınar, E.: A common fixed point theorem of a Gregus type on convex cone metric spaces. J. Comput. Anal. Appl. 13(4), 609–621 (2011)
Karapınar, E.: Some nonunique fixed point theorems of Ciric type on cone metric spaces. Abstr. Appl. Anal. 2010, Article ID 123094 (2010). https://doi.org/10.1155/2010/123094
Karapınar, K.: Couple fixed point theorems for nonlinear contractions in cone metric spaces. Comput. Math. Appl. 59(12), 3656–3668 (2010). https://doi.org/10.1016/j.camwa.2010.03.062
Karapınar, E.: Fixed point theorems in cone Banach spaces. Fixed Point Theory Appl. 2009, Article ID 609281 (2009). https://doi.org/10.1155/2009/609281
Abdeljawad, T., Karapınar, E.: Quasi-cone metric spaces and generalizations of Caristi Kirk’s theorem. Fixed Point Theory Appl. 2009, Article ID 574387 (2009). https://doi.org/10.1155/2009/574387
Karapınar, E., Fulga, A.: On Wong type contractions. Mathematics 8(4), 649 (2020). https://doi.org/10.3390/math8040649
Marasi, H.R., Afshari, H., Daneshbastam, M., Zhai, C.B.: Fixed points of mixed monotone operators for existence and uniqueness of nonlinear fractional differential equations. J. Contemp. Math. Anal. 52, 8C13 (2017)
Liu, H., Xu, S.: Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings. Fixed Point Theory Appl. 2013, 320 (2013)
Lv, X.Y., Feng, Y.Q.: Some fixed point theorems for Reich type contraction in generalized metric spaces. J. Math. Anal. 9(5), 80–88 (2018)
Shah, M.H., Simić, S., Hussain, N., Sretenović, A., Radenović, S.: Common fixed points for occasionally weakly compatible pairs on cone metric type spaces. J. Comput. Anal. Appl. 14(2), 290–297 (2012)
Shojaat, H., Afshari, H., Asgari, M.S.: A new class of mixed monotone operators with concavity and applications to fractional differential equations. TWMS J. Appl. Eng. Math. 11(1), 122–133 (2021)
Yosida, K.: Functional Analysis. Beijing World Publishing Corporation (1999)
Rudin, W.: Functional Analysis and Its Applications. McGraw-Hill, New York (1991)
Ahmed, A., Salunke, J.N.: Algebra cone generalized b-metric space over Banach algebra and fixed point theorems of generalized Lipschitz mappings. Asian-Eur. J. Math. 11(3), 11 (2018)
Hussain, N., Shah, M.H.: KKM mappings in cone b-metric spaces. Comput. Math. Appl. 62(4), 1677–1684 (2011)
Shaddad, F., Noorani, M., Salmi, Md.: Fixed point results in quasi-cone metric spaces. Abstr. Appl. Anal. 2013, Article ID 303626 (2013)
Acknowledgements
The authors thank their universities.
Funding
We declare that funding is not applicable for our paper.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fulga, A., Afshari, H. & Shojaat, H. Common fixed point theorems on quasi-cone metric space over a divisible Banach algebra. Adv Differ Equ 2021, 306 (2021). https://doi.org/10.1186/s13662-021-03464-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03464-z
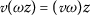 ;
; ,
,  ;
;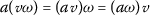 ;
; .
. for all
for all  and
and 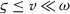 ;
; for all
for all  and
and 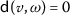 if and only if
if and only if  ,
, for all
for all  ,
,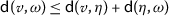 ,
,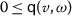 for all
for all  ,
,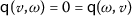 if and only if
if and only if  ,
,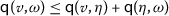 ,
, (bi)-converges to
(bi)-converges to  if for
if for 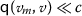 and
and  for
for 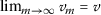 or
or  .
.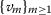 is a (l)(left)-Cauchy ((r)(right)-Cauchy)) if for
is a (l)(left)-Cauchy ((r)(right)-Cauchy)) if for  (respectively,
(respectively, 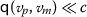 for
for  is a bi-Cauchy if for
is a bi-Cauchy if for 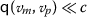 for
for  for all
for all  ;
; for all
for all  .
.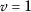 ,
, 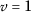 ,
, 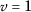 ,
, 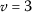 ,
,  ,
,  ,
,