In this section, we use the Lyapunov method to show the global asymptotic stability of the model’s steady states. For formation of Lyapunov functionals, we follow the works [64, 65]. Denote \(U=U(t)\), where \(U\in (S,L,I,E,Y,V,C^{I},C^{Y})\).
Let a function \(\Phi _{j}(S,L,I,E,Y,V,C^{I},C^{Y})\) and \(\Upsilon _{j}^{{\prime }}\) be the largest invariant subset of
$$ \Upsilon _{j}= \biggl\{ \bigl(S,L,I,E,Y,V,C^{I},C^{Y} \bigr): \frac{d\Phi _{j}}{dt}=0 \biggr\} , \quad j=0,1,2,\ldots,7. $$
We define a function \(\digamma (x)=x-1-\ln x\).
Theorem 1
If \(\Re _{1}\leq 1\) and \(\Re _{2}\leq 1\), then  is globally asymptotically stable (GAS).
is globally asymptotically stable (GAS).
Proof
We define a Lyapunov functional as follows:
$$\begin{aligned} \Phi _{0} & =\mathcal{P}S_{0}\digamma \biggl( \frac{S}{S_{0}} \biggr) + \lambda \mathcal{H}_{3}L+ ( \gamma + \lambda ) I+ \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y+ \frac{\mathcal{P}\vartheta _{1}S_{0}}{\varepsilon }V \\ &\quad{}+\frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}+ \lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{ \kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa ) \\ &\quad{}\times \bigl[ \vartheta _{1}V(\varkappa )+\vartheta _{2}I( \varkappa ) \bigr] \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma + \lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa ) \bigl[ \vartheta _{1}V(\varkappa )+\vartheta _{2}I(\varkappa ) \bigr] \,d \varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}L(\varkappa )\,d\varkappa \,d \boldsymbol{\ell }+ \frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa )Y( \varkappa )\,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}E(\varkappa )\,d \varkappa \,d\boldsymbol{ \ell }+ \frac{b\mathcal{P}\vartheta _{1}S_{0}}{\varepsilon }\int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}I(\varkappa )\,d\varkappa \,d \boldsymbol{ \ell }. \end{aligned}$$
Clearly, \(\Phi _{0}(S,L,I,E,Y,V,C^{I},C^{Y})>0\) for all \(S,L,I,E,Y,V,C^{I},C^{Y}>0\), and \(\Phi _{0}(S_{0},0,0,0,0,0, 0,0)=0\). We calculate \(\frac{d\Phi _{0}}{dt}\) along the solutions of model (5) as follows:
$$\begin{aligned} \frac{d\Phi _{0}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{0}}{S} \biggr) ( \eta - \varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) +\lambda \mathcal{H}_{3} \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}(\boldsymbol{\ell })S(t-\boldsymbol{\ell }) \\ &\quad {} \times \bigl\{ \vartheta _{1}V(t-\boldsymbol{\ell })+ \vartheta _{2}I(t- \boldsymbol{\ell }) \bigr\} \,d\boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] + ( \gamma +\lambda ) \biggl[ \beta \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}(\boldsymbol{\ell })S(t-\boldsymbol{\ell }) \\ & \quad {}\times \bigl\{ \vartheta _{1}V(t-\boldsymbol{\ell })+ \vartheta _{2}I(t- \boldsymbol{\ell }) \bigr\} \,d\boldsymbol{\ell }+ \lambda \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}(\boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d \boldsymbol{ \ell }-aI-\mu _{1}C^{I}I \biggr] \\ &\quad{}+\frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl[ \varphi \vartheta _{3}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })\,d \boldsymbol{\ell }+rY- ( \psi + \omega ) E \biggr] \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl[ \psi \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\delta Y-\mu _{2}C^{Y}Y \biggr] \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{0}}{\varepsilon } \biggl[ b \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t- \boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \bigl( \sigma _{2}C^{Y}Y- \pi _{2}C^{Y} \bigr) +\mathcal{P} ( \vartheta _{1}SV+ \vartheta _{2}SI ) -\lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \\ &\quad{}\times S(t-\boldsymbol{\ell }) \bigl[ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }-\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \\ &\quad{}\times \bigl[ \vartheta _{1}V(t-\boldsymbol{\ell })+\vartheta _{2}I(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }+\lambda ( \gamma + \lambda ) \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \bigl[ L-L(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \bigl[ SY-S(t- \boldsymbol{\ell })Y(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \\ &\quad{}\times \bigl[ E-E(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }+ \frac{b\mathcal{P}\vartheta _{1}S_{0}}{\varepsilon } \int _{0}^{ \kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \bigl[ I-I(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }. \end{aligned}$$
(9)
Summing the terms of Eq. (9), we obtain
$$\begin{aligned} \frac{d\Phi _{0}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{0}}{S} \biggr) ( \eta - \varrho S ) +\mathcal{P}\vartheta _{2}S_{0}I-a ( \lambda + \gamma ) I+ \frac{b\mathcal{P}\vartheta _{1}\mathcal{H}_{6}S_{0}}{\varepsilon }I+\mathcal{P}\vartheta _{3}S_{0}Y \\ &\quad{}- \frac{\mathcal{P} [ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega ] }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}. \end{aligned}$$
Using \(S_{0}=\eta /\varrho \), we obtain
$$\begin{aligned} \frac{d\Phi _{0}}{dt} & =-\varrho \mathcal{P}\frac{(S-S_{0})^{2}}{S}+a ( \lambda +\gamma ) ( \Re _{1}-1 ) I+ \frac{\mathcal{P} [ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega ] }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} ( \Re _{2}-1 ) Y \\ &\quad{}- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}. \end{aligned}$$
Since \(r<\delta \) and \(0<\mathcal{H}_{5}\leq 1\), then \(\delta -r\mathcal{H}_{5}>0\). Therefore, \(\frac{d\Phi _{0}}{dt}\leq 0\) for all \(S,I,Y,C^{I},C^{Y}>0\); moreover, \(\frac{d\Phi _{0}}{dt}=0\) when \((S(t),I(t),Y(t),C^{I}(t),C^{Y}(t))=(S_{0},0,0,0,0)\). The solutions of system (5) converge to \(\Upsilon _{0}^{{\prime }}\). The set \(\Upsilon _{0}^{{\prime }}\) includes elements with \((S(t),I(t),Y(t),C^{I}(t),C^{Y}(t))=(S_{0},0,0,0,0)\). Then \(\frac{dS(t)}{dt}=\frac{dY(t)}{dt}=0\) and the first and fifth equations of system (5) become
$$\begin{aligned} &0 =\frac{dS(t)}{dt}=\eta -\varrho S_{0}-\vartheta _{1}S_{0}V(t), \\ &0 =\frac{dY(t)}{dt}=\psi \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }, \end{aligned}$$
which give \(V(t)=E(t)=0\) for all t. In addition, we have \(\frac{dI(t)}{dt}=0\), and from the third equation of system (5) we have
$$ 0=\frac{dI(t)}{dt}=\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }, $$
which yields \(L(t)=0\) for all t and hence 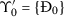 . Applying Lyapunov–LaSalle asymptotic stability (LLAS) theorem [66–68], we get that
. Applying Lyapunov–LaSalle asymptotic stability (LLAS) theorem [66–68], we get that 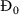 is GAS. □
is GAS. □
The following equalities are needed in the next theorems:
$$\begin{aligned} & \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) = \biggl[ \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{n}}{S_{n}V_{n}L} \biggr) +\ln \biggl( \frac{S_{n}}{S} \biggr) +\ln \biggl( \frac{V_{n}L}{VL_{n}} \biggr) \biggr] , \\ & \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) = \biggl[ \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{n}}{S_{n}V_{n}I} \biggr) +\ln \biggl( \frac{S_{n}}{S} \biggr) +\ln \biggl( \frac{V_{n}I}{VI_{n}} \biggr) \biggr] , \\ & \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) = \biggl[ \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{n}}{S_{n}I_{n}L} \biggr) +\ln \biggl( \frac{S_{n}}{S} \biggr) +\ln \biggl( \frac{I_{n}L}{IL_{n}} \biggr) \biggr] , \\ & \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) = \biggl[ \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{n}I} \biggr) +\ln \biggl( \frac{S_{n}}{S} \biggr) \biggr] , \\ & \ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) =\ln \biggl( \frac{L(t-\boldsymbol{\ell })I_{n}}{L_{n}I} \biggr) +\ln \biggl( \frac{L_{n}I}{LI_{n}} \biggr) , \\ & \ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) =\ln \biggl( \frac{I(t-\boldsymbol{\ell })V_{n}}{I_{n}V} \biggr) +\ln \biggl( \frac{I_{n}V}{IV_{n}} \biggr) ,\quad \mbox{where } n=1,3,5,6,7. \end{aligned}$$
(10)
Further,
$$\begin{aligned} & \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) =\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{m}}{S_{m}Y_{m}E} \biggr) +\ln \biggl( \frac{S_{m}}{S} \biggr) +\ln \biggl( \frac{Y_{m}E}{YE_{m}} \biggr) , \\ & \ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) =\ln \biggl( \frac{E(t-\boldsymbol{\ell })Y_{m}}{E_{m}Y} \biggr) +\ln \biggl( \frac{YE_{m}}{Y_{m}E} \biggr) ,\quad \text{where }m=2,4,5,6,7. \end{aligned}$$
(11)
Theorem 2
Let \(\Re _{1}>1\), \(\Re _{2}/\Re _{1}\leq 1\), and \(\Re _{3}\leq 1\), then  is GAS.
is GAS.
Proof
Define a functional as follows:
$$\begin{aligned} \Phi _{1} & =\mathcal{P}S_{1}\digamma \biggl( \frac{S}{S_{1}} \biggr) + \lambda \mathcal{H}_{3}L_{1} \digamma \biggl( \frac{L}{L_{1}} \biggr) + ( \gamma +\lambda ) I_{1}\digamma \biggl( \frac{I}{I_{1}} \biggr) + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{1}}{\varepsilon }V_{1}\digamma \biggl( \frac{V}{V_{1}} \biggr) + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ &\quad{}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{1}V_{1}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{1}V_{1}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{1}I_{1} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{1}I_{1}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{1}\beta ( \gamma + \lambda ) S_{1}V_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{1}V_{1}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{2}\beta ( \gamma + \lambda ) S_{1}I_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{1}I_{1}} \biggr) \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{1} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{L(\varkappa )}{L_{1}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa )Y(\varkappa )\,d \varkappa \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}E(\varkappa )\,d \varkappa \,d\boldsymbol{ \ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{1}I_{1}}{\varepsilon }\int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{I(\varkappa )}{I_{1}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }. \end{aligned}$$
Calculate \(\frac{d\Phi _{1}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{1}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{1}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) +\lambda \mathcal{H}_{3} \biggl( 1- \frac{L_{1}}{L} \biggr) \\ &\quad{}\times \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad{}+ ( \gamma +\lambda ) \biggl( 1-\frac{I_{1}}{I} \biggr) \biggl[ \beta \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ & \quad{} +\lambda \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-aI-\mu _{1}C^{I}I \biggr] \\ &\quad {} +\frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl[ \varphi \vartheta _{3}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })\,d \boldsymbol{\ell } \\ & \quad{} +rY- ( \psi +\omega ) E \biggr] + \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\delta Y-\mu _{2}C^{Y}Y \biggr] \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{1}}{\varepsilon } \biggl( 1- \frac{V_{1}}{V} \biggr) \biggl[ b \int _{0}^{\kappa _{6}} \bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] \\ &\quad{}+\frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \bigl( \sigma _{2}C^{Y}Y-\pi _{2}C^{Y} \bigr) \\ &\quad{}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{1}V_{1} \\ &\quad {}\times \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{1}V_{1}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{1}V_{1}}+\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{1}I_{1} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{1}I_{1}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I_{1}}+\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{1}\beta ( \gamma +\lambda ) S_{1}V_{1} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{1}V_{1}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{1}V_{1}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\beta ( \gamma +\lambda ) S_{1}I_{1} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{1}I_{1}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I_{1}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{1} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L}{L_{1}}- \frac{L(t-\boldsymbol{\ell })}{L_{1}}+\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \bigl[ SY-S(t- \boldsymbol{\ell })Y(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad {}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \bigl[ E-E(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{b\mathcal{P}\vartheta _{1}S_{1}I_{1}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \biggl[ \frac{I}{I_{1}}- \frac{I(t-\boldsymbol{\ell })}{I_{1}}+\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \biggr] \,d\boldsymbol{ \ell }. \end{aligned}$$
(12)
Summing the terms of Eq. (12), we get
$$\begin{aligned} \frac{d\Phi _{1}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{1}}{S} \biggr) ( \eta -\varrho S ) +\mathcal{P}\vartheta _{2}S_{1}I+ \mathcal{P}\vartheta _{3}S_{1}Y\\ &\quad {}-\vartheta _{1}\lambda \mathcal{H}_{3} ( 1- \beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{1}}{L}\,d \boldsymbol{\ell } \\ &\quad{}-\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{1}}{L}\,d\boldsymbol{\ell }+ \lambda \mathcal{H}_{3} ( \lambda +\gamma ) L_{1}-a ( \lambda + \gamma ) I \\ &\quad{}-\vartheta _{1}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{1}}{I}\,d\boldsymbol{\ell }\\ &\quad {}- \vartheta _{2}\beta ( \gamma +\lambda ) \int _{0}^{ \kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })I_{1}}{I}\,d\boldsymbol{\ell } \\ &\quad{}-\lambda ( \lambda +\gamma ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \frac{L(t-\boldsymbol{\ell })I_{1}}{I}\,d\boldsymbol{\ell }+a ( \lambda +\gamma ) I_{1}\\ &\quad {}+\mu _{1} ( \lambda +\gamma ) C^{I}I_{1}+ \frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}Y- \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y \\ &\quad{}-\frac{\mathcal{P}b\vartheta _{1}S_{1}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \frac{I(t-\boldsymbol{\ell })V_{1}}{V}\,d\boldsymbol{\ell }+\mathcal{P}\vartheta _{1}S_{1}V_{1}\\ &\quad {}- \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{1}V_{1}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{1}V_{1}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda ( \gamma +\lambda ) L_{1} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{b\mathcal{P}\vartheta _{1}S_{1}\mathcal{H}_{6}}{\varepsilon }I+\frac{\mathcal{P}b\vartheta _{1}S_{1}I_{1}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
The steady state conditions for 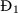 are given by
are given by
$$\begin{aligned} & \eta =\varrho S_{1}+\vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1}, \qquad \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1} ) = ( \lambda +\gamma ) L_{1}, \\ & \beta \mathcal{H}_{2} ( \vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1} ) +\lambda \mathcal{H}_{3}L_{1}=aI_{1} \qquad V_{1}=\frac{b\mathcal{H}_{6}I_{1}}{\varepsilon }. \end{aligned}$$
Then we get
$$ \mathcal{P} ( \vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1} ) =a ( \lambda +\gamma ) I_{1}. $$
Further, we obtain
$$\begin{aligned} \frac{d\Phi _{1}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{1}}{S} \biggr) ( \varrho S_{1}-\varrho S ) +\mathcal{P} ( \vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1} ) \biggl( 1- \frac{S_{1}}{S} \biggr) +\mathcal{P}\vartheta _{3}S_{1}Y \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{1}V_{1}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{1}}{S_{1}V_{1}L}\,d \boldsymbol{\ell }\\ &\quad {}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{1}}{S_{1}I_{1}L}\,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{1}\mathcal{H}_{3} ( 1-\beta ) ( \vartheta _{1}S_{1}V_{1}+\vartheta _{2}S_{1}I_{1} ) \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{1}V_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{1}}{S_{1}V_{1}I}\,d \boldsymbol{\ell }\\ &\quad {}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I}\,d \boldsymbol{\ell }\\ &\quad {}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \frac{L(t-\boldsymbol{\ell })I_{1}}{L_{1}I}\,d\boldsymbol{\ell } \\ &\quad{}+\mathcal{P} ( \vartheta _{1}S_{1}V_{1}+ \vartheta _{2}S_{1}I_{1} ) +\mu _{1} ( \lambda +\gamma ) C^{I}I_{1}- \frac{\mathcal{P} [ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega ] }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y\\ &\quad {}- \frac{\mathcal{P}\vartheta _{1}S_{1}V_{1}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\frac{I(t-\boldsymbol{\ell })V_{1}}{I_{1}V}\,d\boldsymbol{\ell }\\ &\quad {}+\mathcal{P} \vartheta _{1}S_{1}V_{1}- \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{1}V_{1}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{1}V_{1}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{1}V_{1}+\vartheta _{2}S_{1}I_{1} ) \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P}\vartheta _{1}S_{1}V_{1}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the equalities given by (10) in case of \(n=1\), we get
$$\begin{aligned} \frac{d\Phi _{1}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{1})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{1}V_{1}+\vartheta _{2}S_{1}I_{1} ) \biggl[ \frac{S_{1}}{S}-1- \ln \biggl( \frac{S_{1}}{S} \biggr) \biggr] \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{1}V_{1} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{1}}{S_{1}V_{1}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{1}}{S_{1}V_{1}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{1}I_{1} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{1}}{S_{1}I_{1}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{1}}{S_{1}I_{1}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{1}V_{1} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{1}}{S_{1}V_{1}I}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{1}}{S_{1}V_{1}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{1}V_{1}+\vartheta _{2}S_{1}I_{1} ) \\ &\quad {}\times\int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L(t-\boldsymbol{\ell })I_{1}}{L_{1}I}-1-\ln \biggl( \frac{L(t-\boldsymbol{\ell })I_{1}}{L_{1}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{1}V_{1}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \biggl[ \frac{I(t-\boldsymbol{\ell })V_{1}}{I_{1}V}-1-\ln \biggl( \frac{I(t-\boldsymbol{\ell })V_{1}}{I_{1}V} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad {}+ \frac{\mathcal{P} [ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega ] }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}\biggl( \frac{\vartheta _{3}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}S_{1}}{ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega }-1 \biggr) Y \\ &\quad{}+\mu _{1} ( \lambda +\gamma ) \biggl( I_{1}- \frac{\pi _{1}}{\sigma _{1}} \biggr) C^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}. \end{aligned}$$
(13)
Therefore, Eq. (13) becomes
$$\begin{aligned} \frac{d\Phi _{1}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{1})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{1}V_{1}+\vartheta _{2}S_{1}I_{1} ) \digamma \biggl( \frac{S_{1}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{1}V_{1}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{1}}{S_{1}V_{1}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{1}I_{1}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{1}}{S_{1}I_{1}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{1}V_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{1}}{S_{1}V_{1}I} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{1}I_{1} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{1}V_{1}+\vartheta _{2}S_{1}I_{1} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\digamma \biggl( \frac{L(t-\boldsymbol{\ell })I_{1}}{L_{1}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{1}V_{1}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \digamma \biggl( \frac{I(t-\boldsymbol{\ell })V_{1}}{I_{1}V} \biggr) \,d \boldsymbol{ \ell }+ \frac{\mathcal{P} [ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega ] }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( \frac{\Re _{2}}{\Re _{1}}-1 \biggr) Y \\ &\quad{}+ \frac{\mu _{1} ( \gamma +\lambda ) [ \pi _{1} ( b\vartheta _{1}\mathcal{H}_{6}+\varepsilon \vartheta _{2} ) +\varrho \varepsilon \sigma _{1} ] }{\sigma _{1} ( b\vartheta _{1}\mathcal{H}_{6}+\varepsilon \vartheta _{2} ) } ( \Re _{3}-1 ) C^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}. \end{aligned}$$
Since \(\Re _{2}/\Re _{1}\leq 1\) and \(\Re _{3}\leq 1\), then \(\frac{d\Phi _{1}}{dt}\leq 0\) for all \(S,L,I,Y,V,C^{I},C^{Y}>0\). Moreover, \(\frac{d\Phi _{1}}{dt}=0\) when \(S=S_{1}\) and \(Y=C^{I}=C^{Y}=\digamma =0\). The solutions of system (5) converge to \(\Upsilon _{1}^{{\prime }}\) which includes elements that satisfy \(S(t)=S_{1}\) and \(\digamma =0\) i.e.
$$\begin{aligned} \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{1}}{S_{1}V_{1}L} & = \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{1}}{S_{1}I_{1}L}= \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{1}}{S_{1}V_{1}I} \\ & =\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{1}I}= \frac{L(t-\boldsymbol{\ell })I_{1}}{L_{1}I}= \frac{I(t-\boldsymbol{\ell })V_{1}}{I_{1}V}=1 \end{aligned}$$
(14)
for all \(t\in {}[ 0,\kappa ]\). If \(S(t)=S_{1}\), then from Eq. (14) we get \(L(t)=L_{1}\), \(I(t)=I_{1}\), and \(V(t)=V_{1}\) for all t. Further, for each element of \(\Upsilon _{1}^{\prime }\), we have \(Y(t)=0\) and then \(\frac{dY(t)}{dt}=0\). The fifth equation of system (5) becomes
$$ 0=\frac{dY(t)}{dt}=\psi \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }, $$
which provides \(E(t)=0\) for all t, and hence  . Therefore, using LLAS theorem we get that
. Therefore, using LLAS theorem we get that  is GAS. □
is GAS. □
Theorem 3
If \(\Re _{2}>1\), \(\Re _{1}/\Re _{2}\leq 1\), and \(\Re _{4}\leq 1\), then  is GAS.
is GAS.
Proof
Define
$$\begin{aligned} \Phi _{2} & =\mathcal{P}S_{2}\digamma \biggl( \frac{S}{S_{2}} \biggr) + \lambda \mathcal{H}_{3}L+ ( \gamma + \lambda ) I+ \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E_{2}\digamma \biggl( \frac{E}{E_{2}} \biggr) + \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{2}\digamma \biggl( \frac{Y}{Y_{2}} \biggr) \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{2}}{\varepsilon }V+ \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}+\lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}(\boldsymbol{\ell }) \int _{t- \boldsymbol{\ell }}^{t}S(\varkappa ) \\ &\quad{}\times \bigl[ \vartheta _{1}V(\varkappa )+\vartheta _{2}I( \varkappa ) \bigr] \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma + \lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa ) \bigl[ \vartheta _{1}V(\varkappa )+\vartheta _{2}I(\varkappa ) \bigr] \,d \varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}L(\varkappa )\,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}} \bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )Y(\varkappa )}{S_{2}Y_{2}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{E(\varkappa )}{E_{2}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{2}}{\varepsilon } \int _{0}^{ \kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}I(\varkappa )\,d\varkappa \,d \boldsymbol{\ell }. \end{aligned}$$
We calculate \(\frac{d\Phi _{2}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{2}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{2}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) \\ &\quad{}+\lambda \mathcal{H}_{3} \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}(\boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t-\boldsymbol{\ell })+\vartheta _{2}I(t- \boldsymbol{\ell }) \bigr\} \,d\boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad{}+ ( \gamma +\lambda ) \biggl[ \beta \int _{0}^{ \kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ &\quad {}+\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell } -aI-\mu _{1}C^{I}I \biggr] \\ & \quad{} + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl( 1-\frac{E_{2}}{E} \biggr) \biggl[ \varphi \vartheta _{3} \int _{0}^{\kappa _{4}} \bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t- \boldsymbol{\ell })\,d\boldsymbol{ \ell }+rY- ( \psi +\omega ) E \biggr] \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1-\frac{Y_{2}}{Y} \biggr) \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\delta Y- \mu _{2}C^{Y}Y \biggr] + \frac{\mathcal{P}\vartheta _{1}S_{2}}{\varepsilon } \\ &\quad{}\times \biggl[ b \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \\ &\quad{}\times \bigl( \sigma _{2}C^{Y}Y-\pi _{2}C^{Y} \bigr) +\mathcal{P} ( \vartheta _{1}SV+ \vartheta _{2}SI ) -\lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \\ &\quad{}\times \bigl[ \vartheta _{1}V(t-\boldsymbol{\ell })+\vartheta _{2}I(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }-\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl[ \vartheta _{1}V(t- \boldsymbol{\ell }) \\ & \quad{} +\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr] \,d \boldsymbol{\ell }+\lambda ( \gamma +\lambda ) \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \bigl[ L-L(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{SY}{S_{2}Y_{2}} \\ & \quad{} -\frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{S_{2}Y_{2}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P} ( \psi +\omega ) E_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E}{E_{2}}-\frac{E(t-\boldsymbol{\ell })}{E_{2}}+ \ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad {}+\frac{b\mathcal{P}\vartheta _{1}S_{2}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \bigl[ I-I(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }. \end{aligned}$$
(15)
By collecting the terms of Eq. (15), we get
$$\begin{aligned} \frac{d\Phi _{2}}{dt} & =\mathcal{P} \biggl[ \biggl( 1-\frac{S_{2}}{S} \biggr) ( \eta -\varrho S ) +\vartheta _{2}S_{2}I+ \vartheta _{3}S_{2}Y-\frac{a ( \lambda +\gamma ) }{\mathcal{P}}I+ \frac{r}{\varphi \mathcal{H}_{4}}Y \\ &\quad {} -\frac{\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{2}}{E}\,d\boldsymbol{\ell }- \frac{r}{\varphi \mathcal{H}_{4}} \frac{YE_{2}}{E}+\frac{\psi +\omega }{\varphi \mathcal{H}_{4}}E_{2}- \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y \\ &\quad {} - \frac{\psi +\omega }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}}\int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \frac{E(t-\boldsymbol{\ell })Y_{2}}{Y}\,d\boldsymbol{\ell }+ \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{2}+ \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y_{2} \\ &\quad {} - \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I}- \frac{\mu _{2}\pi _{2} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}\\ &\quad {}+ \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d\boldsymbol{\ell } \\ & \quad{} + \frac{ ( \psi +\omega ) E_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell }+ \frac{b\vartheta _{1}S_{2}\mathcal{H}_{6}}{\varepsilon }I \biggr] . \end{aligned}$$
Using the steady state conditions for 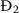
$$ \eta =\varrho S_{2}+\vartheta _{3}S_{2}Y_{2}, \qquad \vartheta _{3}S_{2}Y_{2}+ \frac{rY_{2}}{\varphi \mathcal{H}_{4}}= \frac{ ( \psi +\omega ) E_{2}}{\varphi \mathcal{H}_{4}}= \frac{\delta ( \psi +\omega ) Y_{2}}{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}, $$
we obtain
$$\begin{aligned} \frac{d\Phi _{2}}{dt} & =\mathcal{P} \biggl[ \biggl( 1-\frac{S_{2}}{S} \biggr) ( \varrho S_{2}-\varrho S ) +\vartheta _{3}S_{2}Y_{2} \biggl( 1-\frac{S_{2}}{S} \biggr) \\ &\quad {}- \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{2}}{S_{2}Y_{2}E}\,d \boldsymbol{\ell }-\frac{rY_{2}}{\varphi \mathcal{H}_{4}} \frac{YE_{2}}{Y_{2}E} \\ &\quad {}+\vartheta _{3}S_{2}Y_{2}+\frac{rY_{2}}{\varphi \mathcal{H}_{4}}- \biggl( \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{5}}+ \frac{rY_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \frac{E(t-\boldsymbol{\ell })Y_{2}}{E_{2}Y}\,d\boldsymbol{\ell } \\ & \quad{} +\vartheta _{3}S_{2}Y_{2}+ \frac{rY_{2}}{\varphi \mathcal{H}_{4}}+ \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y_{2}- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I}- \frac{\mu _{2}\pi _{2} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ & \quad{} +\frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \biggl( \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{5}}+ \frac{rY_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell } \\ & \quad {} + \frac{a ( \lambda +\gamma ) }{\mathcal{P}} \biggl\{ \frac{\mathcal{P}S_{2} ( \varepsilon \vartheta _{2}+b\vartheta _{1}\mathcal{H}_{6} ) }{a\varepsilon ( \lambda +\gamma ) }-1 \biggr\} I \biggr] . \end{aligned}$$
Using the equalities given by (11) in case of \(m=2\), we get
$$\begin{aligned} \frac{d\Phi _{2}}{dt} & =-\mathcal{P} \biggl[ \varrho \frac{ ( S-S_{2} ) ^{2}}{S}+ \vartheta _{3}S_{2}Y_{2} \biggl\{ \frac{S_{2}}{S}-1-\ln \biggl( \frac{S_{2}}{S} \biggr) \biggr\} + \frac{rY_{2}}{\varphi \mathcal{H}_{4}} \biggl\{ \frac{YE_{2}}{Y_{2}E}-1- \ln \biggl( \frac{YE_{2}}{Y_{2}E} \biggr) \biggr\} \\ & \quad{} +\frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \biggl\{ \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{2}}{S_{2}Y_{2}E}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{2}}{S_{2}Y_{2}E} \biggr) \biggr\} \,d\boldsymbol{\ell } \\ & \quad{} + \biggl( \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{5}}+\frac{rY_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl\{ \frac{E(t-\boldsymbol{\ell })Y_{2}}{E_{2}Y}-1-\ln \biggl( \frac{E(t-\boldsymbol{\ell })Y_{2}}{E_{2}Y} \biggr) \biggr\} \,d \boldsymbol{\ell } \\ & \quad {} - \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I}+ \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( Y_{2}-\frac{\pi _{2}}{\sigma _{2}} \biggr) C^{Y} \biggr] \\ &\quad {}+a ( \lambda +\gamma ) \biggl( \frac{\mathcal{P}S_{2} ( \varepsilon \vartheta _{2}+b\vartheta _{1}\mathcal{H}_{6} ) }{a\varepsilon ( \lambda +\gamma ) }-1 \biggr) I. \end{aligned}$$
(16)
Therefore, Eq. (16) becomes
$$\begin{aligned} \frac{d\Phi _{2}}{dt} & =-\mathcal{P} \biggl[ \varrho \frac{ ( S-S_{2} ) ^{2}}{S}+ \frac{rY_{2}}{\varphi \mathcal{H}_{4}} \digamma \biggl( \frac{YE_{2}}{Y_{2}E} \biggr)\\ &\quad {} + \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl\{ \digamma \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{2}}{S_{2}Y_{2}E} \biggr)+\digamma \biggl( \frac{S_{2}}{S} \biggr) \biggr\} \,d \boldsymbol{\ell } \\ & \quad{}+ \biggl( \frac{\vartheta _{3}S_{2}Y_{2}}{\mathcal{H}_{5}}+\frac{rY_{2}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \digamma \biggl( \frac{E(t-\boldsymbol{\ell })Y_{2}}{E_{2}Y} \biggr) \,d \boldsymbol{ \ell } \\ & \quad {} - \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I}+ \frac{\mu _{2} ( \psi +\omega ) ( \varrho \sigma _{2}+\vartheta _{3}\pi _{2} ) }{\vartheta _{3}\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} ( \Re _{4}-1 ) C^{Y} \biggr] \\ &\quad {}+a ( \lambda +\gamma ) \biggl( \frac{\Re _{1}}{\Re _{2}}-1 \biggr) I. \end{aligned}$$
Thus, if \(\Re _{1}/\Re _{2}\leq 1\) and \(\Re _{4}\leq 1\), then \(\frac{d\Phi _{2}}{dt}\leq 0\) for all \(S,I,E,Y,C^{I},C^{Y}>0\). Moreover, \(\frac{d\Phi _{2}}{dt}=0\) when \((S,E,Y,I,C^{I},C^{Y})=(S_{2},E_{2},Y_{2},0,0,0)\). The solutions of system (5) converge to \(\Upsilon _{2}^{{\prime }}\) which includes elements with \((S(t),E(t),Y(t),I(t),C^{I}(t),C^{Y}(t))=(S_{2},E_{2},Y_{2},0,0,0)\). Then we have \(\frac{dS(t)}{dt}=0\), and the first equation of system (5) becomes
$$ 0=\frac{dS(t)}{dt}=\eta -\varrho S_{2}-\vartheta _{1}S_{2}V(t)- \vartheta _{3}S_{2}Y_{2}, $$
which yields \(V(t)=0\) for all t. Moreover, we have \(\frac{dI(t)}{dt}=0\) and from the third equation of system (5) we get
$$ 0=\frac{dI(t)}{dt}=\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }, $$
which implies that \(L(t)=0\) for all t. Therefore,  . Applying LLAS theorem, we get
. Applying LLAS theorem, we get  is GAS. □
is GAS. □
Theorem 4
Let \(\Re _{3}>1\) and \(\Re _{5}\leq 1\), then 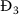 is GAS.
is GAS.
Proof
Define a functional as follows:
$$\begin{aligned} \Phi _{3} & =\mathcal{P}S_{3}\digamma \biggl( \frac{S}{S_{3}} \biggr) + \lambda \mathcal{H}_{3}L_{3} \digamma \biggl( \frac{L}{L_{3}} \biggr) + ( \gamma +\lambda ) I_{3}\digamma \biggl( \frac{I}{I_{3}} \biggr) + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{3}}{\varepsilon }V_{3}\digamma \biggl( \frac{V}{V_{3}} \biggr) + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C_{3}^{I}\digamma \biggl( \frac{C^{I}}{C_{3}^{I}} \biggr) + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ &\quad{}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{3}V_{3}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{3}V_{3}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{3}I_{3} \\ &\quad \times{} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{3}I_{3}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }+\vartheta _{1}\beta ( \gamma + \lambda ) S_{3}V_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \\ &\quad{}\times \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{3}V_{3}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad {}+\vartheta _{2}\beta ( \gamma + \lambda ) S_{3}I_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{3}I_{3}} \biggr) \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{3} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{L(\varkappa )}{L_{3}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad {}+\frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa )Y(\varkappa )\,d \varkappa \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}E(\varkappa )\,d \varkappa \,d\boldsymbol{ \ell } \\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{3}I_{3}}{\varepsilon }\int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{I(\varkappa )}{I_{3}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }. \end{aligned}$$
(17)
We calculate \(\frac{d\Phi _{3}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{3}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{3}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) +\lambda \mathcal{H}_{3} \biggl( 1- \frac{L_{3}}{L} \biggr) \\ &\quad{}\times \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad{}+ ( \gamma +\lambda ) \biggl( 1-\frac{I_{3}}{I} \biggr) \biggl[ \beta \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ & \quad{} +\lambda \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-aI-\mu _{1}C^{I}I \biggr] \\ &\quad {}+\frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl[ \varphi \vartheta _{3}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })\,d \boldsymbol{\ell }+rY- ( \psi +\omega ) E \biggr] \\ & \quad{} + \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\delta Y-\mu _{2}C^{Y}Y \biggr] \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{3}}{\varepsilon } \biggl( 1- \frac{V_{3}}{V} \biggr) \biggl[ b \int _{0}^{\kappa _{6}} \bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \\ &\quad{}\times \biggl( 1-\frac{C_{3}^{I}}{C^{I}} \biggr) \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \bigl( \sigma _{2}C^{Y}Y-\pi _{2}C^{Y} \bigr) \\ &\quad{}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{3}V_{3} \\ &\quad {}\times \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{3}V_{3}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{3}V_{3}}+\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{3}I_{3} \\ &\quad {}\times \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{3}I_{3}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I_{3}}+\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{1}\beta ( \gamma +\lambda ) S_{3}V_{3} \\ &\quad {}\times \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{3}V_{3}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{3}V_{3}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\beta ( \gamma +\lambda ) S_{3}I_{3} \\ &\quad {}\times \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{3}I_{3}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I_{3}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{3} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L}{L_{3}}- \frac{L(t-\boldsymbol{\ell })}{L_{3}}+\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \bigl[ SY-S(t- \boldsymbol{\ell })Y(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad {}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \bigl[ E-E(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{b\mathcal{P}\vartheta _{1}S_{3}I_{3}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \biggl[ \frac{I}{I_{3}}- \frac{I(t-\boldsymbol{\ell })}{I_{3}}+\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \biggr] \,d\boldsymbol{ \ell }. \end{aligned}$$
(18)
Collecting the terms of Eq. (18), we derive
$$\begin{aligned} \frac{d\Phi _{3}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{3}}{S} \biggr) ( \eta -\varrho S ) +\mathcal{P}\vartheta _{2}S_{3}I+ \mathcal{P}\vartheta _{3}S_{3}Y-\vartheta _{1}\lambda \mathcal{H}_{3} ( 1- \beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \\ &\quad{}\times \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{3}}{L}\,d \boldsymbol{\ell }-\vartheta _{2} \lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{3}}{L}\,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( \lambda +\gamma ) L_{3}-a ( \lambda +\gamma ) I-\vartheta _{1}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{3}}{I}\,d\boldsymbol{\ell } \\ &\quad{}-\vartheta _{2}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })I_{3}}{I}\,d\boldsymbol{\ell }\\ &\quad {}- \lambda ( \lambda +\gamma ) \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\frac{L(t-\boldsymbol{\ell })I_{3}}{I}\,d\boldsymbol{\ell }+a ( \lambda +\gamma ) I_{3}+\mu _{1} ( \lambda + \gamma ) C^{I}I_{3} \\ &\quad{}+ \frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}Y- \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y- \frac{\mathcal{P}b\vartheta _{1}S_{3}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\frac{I(t-\boldsymbol{\ell })V_{3}}{V}\,d\boldsymbol{\ell } \\ &\quad{}+ \mathcal{P}\vartheta _{1}S_{3}V_{3}- \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C^{I}- \mu _{1} ( \lambda +\gamma ) C_{3}^{I}I \\ &\quad{}+ \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C_{3}^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ &\quad{}+ \lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{3}V_{3} \int _{0}^{ \kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+ \lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{3}V_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d\boldsymbol{\ell } \\ &\quad{} + \lambda ( \gamma +\lambda ) L_{3} \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}(\boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{b\mathcal{P}\vartheta _{1}S_{3}\mathcal{H}_{6}}{\varepsilon }I+\frac{b\mathcal{P}\vartheta _{1}S_{3}I_{3}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the steady state conditions for 
$$\begin{aligned} & \eta =\varrho S_{3}+\vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3}, \qquad \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3} ) = ( \lambda +\gamma ) L_{3}, \\ & \beta \mathcal{H}_{2} ( \vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3} ) +\lambda \mathcal{H}_{3}L_{3}= \bigl( a+\mu _{1}C_{3}^{I} \bigr) I_{3}, \qquad I_{3}= \frac{\pi _{1}}{\sigma _{1}}, \qquad V_{3}= \frac{b\mathcal{H}_{6}}{\varepsilon }I_{3}, \end{aligned}$$
we get
$$ \mathcal{P} ( \vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3} ) = ( \lambda +\gamma ) \bigl( a+\mu _{1}C_{3}^{I} \bigr) I_{3}. $$
Further, we obtain
$$\begin{aligned} \frac{d\Phi _{3}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{3}}{S} \biggr) ( \varrho S_{3}-\varrho S ) +\mathcal{P} ( \vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3} ) \biggl( 1- \frac{S_{3}}{S} \biggr) +\mathcal{P}\vartheta _{3}S_{3}Y \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{3}V_{3}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{3}}{S_{3}V_{3}L}\,d \boldsymbol{\ell }-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{3}I_{3} \\ &\quad{}\times \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{3}}{S_{3}I_{3}L}\,d \boldsymbol{\ell }+\lambda \mathcal{H}_{1}\mathcal{H}_{3} ( 1-\beta ) ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{3}V_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{3}}{S_{3}V_{3}I}\,d \boldsymbol{\ell }-\beta ( \gamma +\lambda ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \\ &\quad{}\times \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I}\,d \boldsymbol{\ell }-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \frac{L(t-\boldsymbol{\ell })I_{3}}{L_{3}I}\,d\boldsymbol{\ell } \\ &\quad{}+\mathcal{P} ( \vartheta _{1}S_{3}V_{3}+ \vartheta _{2}S_{3}I_{3} ) - \frac{\mathcal{P} [ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega ] }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y-\frac{\mathcal{P}\vartheta _{1}S_{3}V_{3}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \\ &\quad{}\times \frac{I(t-\boldsymbol{\ell })V_{3}}{I_{3}V}\,d\boldsymbol{\ell }+ \mathcal{P}\vartheta _{1}S_{3}V_{3}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}+ \lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{3}V_{3} \\ &\quad{}\times \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{3}V_{3}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P}\vartheta _{1}S_{3}V_{3}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the equalities given by (10) in case of \(n=3\), we get
$$\begin{aligned} \frac{d\Phi _{3}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{3})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) \biggl[ \frac{S_{3}}{S}-1- \ln \biggl( \frac{S_{3}}{S} \biggr) \biggr] \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{3}V_{3} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{3}}{S_{3}V_{3}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{3}}{S_{3}V_{3}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{3}I_{3} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{3}}{S_{3}I_{3}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{3}}{S_{3}I_{3}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{3}V_{3} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{3}}{S_{3}V_{3}I}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{3}}{S_{3}V_{3}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) \\ &\quad {}\times\int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L(t-\boldsymbol{\ell })I_{3}}{L_{3}I}-1-\ln \biggl( \frac{L(t-\boldsymbol{\ell })I_{3}}{L_{3}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{3}V_{3}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \biggl[ \frac{I(t-\boldsymbol{\ell })V_{3}}{I_{3}V}-1-\ln \biggl( \frac{I(t-\boldsymbol{\ell })V_{3}}{I_{3}V} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}+\mathcal{P}\vartheta _{3} \biggl( S_{3}- \frac{ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega }{\vartheta _{3}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) Y- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}. \end{aligned}$$
(19)
Therefore, Eq. (19) becomes
$$\begin{aligned} \frac{d\Phi _{3}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{3})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) \digamma \biggl( \frac{S_{3}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{3}V_{3}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{3}}{S_{3}V_{3}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{3}I_{3}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{3}}{S_{3}I_{3}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{3}V_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{3}}{S_{3}V_{3}I} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{3}I_{3} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\digamma \biggl( \frac{L(t-\boldsymbol{\ell })I_{3}}{L_{3}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{3}V_{3}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \digamma \biggl( \frac{I(t-\boldsymbol{\ell })V_{3}}{I_{3}V} \biggr) \,d \boldsymbol{ \ell }\\ &\quad {}+\mathcal{P}\vartheta _{3} ( S_{3}-S_{5} ) Y- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}. \end{aligned}$$
Hence, if \(\Re _{5}\leq 1\), then  does not exist since \(E_{5}\leq 0\) and \(Y_{5}\leq 0\). In this case
does not exist since \(E_{5}\leq 0\) and \(Y_{5}\leq 0\). In this case
$$\begin{aligned} &\frac{dE(t)}{dt} =\varphi \vartheta _{3} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t- \boldsymbol{\ell })\,d\boldsymbol{ \ell }+rY(t)- ( \psi +\omega ) E(t) \leq 0, \\ &\frac{dY(t)}{dt} =\psi \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\delta Y(t)-\mu _{2}C^{Y}Y\leq 0. \end{aligned}$$
Now we want to find the value S̄ such that, for all \(0< S(t)\leq \bar{S}\), we get \(\frac{dE(t)}{dt}\leq 0\) and \(\frac{dY(t)}{dt}\leq 0\). Let us consider
$$\begin{aligned} & \frac{d}{dt} \biggl[ \frac{1}{\mathcal{H}_{4}}E+ \frac{\psi +\omega }{\psi \mathcal{H}_{4}\mathcal{H}_{5}}Y+ \frac{\varphi \vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa )Y( \varkappa )\,d\varkappa \,d\boldsymbol{\ell }\\ &\qquad {}+ \frac{\psi +\omega }{\mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}E(\varkappa )\,d\varkappa \,d \boldsymbol{ \ell } \biggr] \\ &\quad =\varphi \vartheta _{3}SY- \frac{ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega }{\psi \mathcal{H}_{4}\mathcal{H}_{5}}Y- \frac{\mu _{2} ( \psi +\omega ) }{\psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y \\ &\quad =\varphi \vartheta _{3} \biggl( S- \frac{ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega }{\varphi \vartheta _{3}\psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) Y- \frac{\mu _{2} ( \psi +\omega ) }{\psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y\leq 0\quad \text{for all }C^{Y},Y>0. \end{aligned}$$
This happens when \(S_{3}\leq \bar{S}= \frac{ ( \delta -r\mathcal{H}_{5} ) \psi +\delta \omega }{\vartheta _{3}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}=S_{5}\). Clearly, \(\frac{d\Phi _{3}}{dt}\leq 0\) for all \(S,L,I,Y,V,C^{Y}>0\), where \(\frac{d\Phi _{3}}{dt}=0\) occurs at \(S=S_{3}\) and \(Y=C^{Y}=0\). The solutions of system (5) converge to \(\Upsilon _{3}^{{\prime }}\) which includes elements satisfying \(S(t)=S_{3}\) and \(\digamma =0\) i.e.
$$\begin{aligned} \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{3}}{S_{3}V_{3}L} & = \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{3}}{S_{3}I_{3}L}= \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{3}}{S_{3}V_{3}I} \\ & =\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{3}I}= \frac{L(t-\boldsymbol{\ell })I_{3}}{L_{3}I}= \frac{I(t-\boldsymbol{\ell })V_{3}}{I_{3}V}=1 \end{aligned}$$
(20)
for all \(t\in {}[ 0,\kappa ]\). If \(S(t)=S_{3}\), then from Eq. (20) we get \(L(t)=L_{3}\), \(I(t)=I_{3}\), and \(V(t)=V_{3}\) for all t. Thus, \(\Upsilon _{3}^{{\prime }}\) contains elements with \(I(t)=I_{3}\), \(V(t)=V_{3}\), \(Y(t)=0\), and then \(\frac{dI(t)}{dt}=0\), \(\frac{dY(t)}{dt}=0\). The third and fifth equations of system (5) become
$$\begin{aligned} &0 =\frac{dI(t)}{dt}=\beta \mathcal{H}_{2} ( \vartheta _{1}S_{3}V_{3}+\vartheta _{2}S_{3}I_{3} ) +\lambda \mathcal{H}_{3}L_{3}-aI_{3}- \mu _{1}C^{I}(t)I_{3}, \\ &0 =\frac{dY(t)}{dt}=\psi \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}E(t- \boldsymbol{\ell })\,d\boldsymbol{\ell }, \end{aligned}$$
which yield \(C^{I}(t)=C_{3}^{I}\) and \(E(t)=0\) for all t. Therefore, 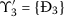 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 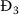 is GAS. □
is GAS. □
Theorem 5
If \(\Re _{4}>1\) and \(\Re _{6}\leq 1\), then  is GAS.
is GAS.
Proof
Let
$$\begin{aligned} \Phi _{4} & =\mathcal{P}S_{4}\digamma \biggl( \frac{S}{S_{4}} \biggr) + \lambda \mathcal{H}_{3}L+ ( \gamma + \lambda ) I+ \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E_{4}\digamma \biggl( \frac{E}{E_{4}} \biggr) + \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{4}\digamma \biggl( \frac{Y}{Y_{4}} \biggr) \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{4}}{\varepsilon }V+ \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{4}^{Y}\digamma \biggl( \frac{C^{Y}}{C_{4}^{Y}} \biggr) \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa ) \bigl[ \vartheta _{1}V(\varkappa )+\vartheta _{2}I(\varkappa ) \bigr] \,d \varkappa \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}S(\varkappa ) \bigl[ \vartheta _{1}V(\varkappa )+\vartheta _{2}I( \varkappa ) \bigr] \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}L(\varkappa )\,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}} \bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )Y(\varkappa )}{S_{4}Y_{4}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{E(\varkappa )}{E_{4}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{4}}{\varepsilon } \int _{0}^{ \kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}I(\varkappa )\,d\varkappa \,d \boldsymbol{\ell }. \end{aligned}$$
Calculate \(\frac{d\Phi _{4}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{4}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{4}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) \\ &\quad{}+\lambda \mathcal{H}_{3} \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}(\boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t-\boldsymbol{\ell })+\vartheta _{2}I(t- \boldsymbol{\ell }) \bigr\} \,d\boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad{}+ ( \gamma +\lambda ) \biggl[ \beta \int _{0}^{ \kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ & \quad{}+\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell } -aI-\mu _{1}C^{I}I \biggr] \\ &\quad {} + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl( 1-\frac{E_{4}}{E} \biggr) \biggl[ \varphi \vartheta _{3} \int _{0}^{\kappa _{4}} \bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t- \boldsymbol{\ell })\,d\boldsymbol{ \ell }+rY- ( \psi +\omega ) E \biggr] \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1-\frac{Y_{4}}{Y} \biggr) \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\delta Y- \mu _{2}C^{Y}Y \biggr] \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{4}}{\varepsilon } \biggl[ b \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t- \boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1-\frac{C_{4}^{Y}}{C^{Y}} \biggr) \bigl( \sigma _{2}C^{Y}Y-\pi _{2}C^{Y} \bigr) +\mathcal{P} ( \vartheta _{1}SV+ \vartheta _{2}SI ) \\ &\quad{}- \lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl[ \vartheta _{1}V(t-\boldsymbol{\ell })+\vartheta _{2}I(t- \boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad {}-\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl[ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr] \,d \boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \bigl[ L-L(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell } \\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{SY}{S_{4}Y_{4}}- \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{S_{4}Y_{4}} \\ & \quad{} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \biggr] \,d \boldsymbol{ \ell }+ \frac{\mathcal{P} ( \psi +\omega ) E_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E}{E_{4}}- \frac{E(t-\boldsymbol{\ell })}{E_{4}} \\ & \quad{} +\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \biggr] \,d \boldsymbol{ \ell }+\frac{b\mathcal{P}\vartheta _{1}S_{4}}{\varepsilon }\int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \bigl[ I-I(t-\boldsymbol{\ell }) \bigr] \,d\boldsymbol{\ell }. \end{aligned}$$
(21)
Summing the terms of Eq. (21), we get
$$\begin{aligned} \frac{d\Phi _{4}}{dt} & =\mathcal{P} \biggl[ \biggl( 1-\frac{S_{4}}{S} \biggr) ( \eta -\varrho S ) +\vartheta _{2}S_{4}I+ \vartheta _{3}S_{4}Y-\frac{a ( \lambda +\gamma ) }{\mathcal{P}}I+ \frac{r}{\varphi \mathcal{H}_{4}}Y \\ & \quad{} -\frac{\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{4}}{E}\,d\boldsymbol{\ell }- \frac{r}{\varphi \mathcal{H}_{4}} \frac{YE_{4}}{E}+\frac{\psi +\omega }{\varphi \mathcal{H}_{4}}E_{4} \\ & \quad{} - \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y- \frac{\psi +\omega }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\frac{E(t-\boldsymbol{\ell })Y_{4}}{Y}\,d\boldsymbol{\ell }+ \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{4} \\ & \quad{} + \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y_{4}- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I}- \frac{\mu _{2}\pi _{2} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}- \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{4}^{Y}Y \\ & \quad{} + \frac{\mu _{2}\pi _{2} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{4}^{Y}+ \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d\boldsymbol{\ell } \\ & \quad{} + \frac{ ( \psi +\omega ) E_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell }+ \frac{b\vartheta _{1}S_{4}\mathcal{H}_{6}}{\varepsilon }I \biggr] . \end{aligned}$$
Using the steady state conditions for 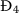
$$\begin{aligned} &\eta =\varrho S_{4}+\vartheta _{3}S_{4}Y_{4}, \qquad Y_{4}= \frac{\pi _{2}}{\sigma _{2}}, \\ &\vartheta _{3}S_{4}Y_{4}+\frac{rY_{4}}{\varphi \mathcal{H}_{4}} = \frac{ ( \psi +\omega ) E_{4}}{\varphi \mathcal{H}_{4}}= \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{4}+ \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{4}^{Y}Y_{4}, \end{aligned}$$
we obtain
$$\begin{aligned} \frac{d\Phi _{4}}{dt} & =\mathcal{P} \biggl[ \biggl( 1-\frac{S_{4}}{S} \biggr) ( \varrho S_{4}-\varrho S ) +\vartheta _{3}S_{4}Y_{4} \biggl( 1-\frac{S_{4}}{S} \biggr)\\ &\quad {} - \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}}\int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{4}}{S_{4}Y_{4}E}\,d\boldsymbol{\ell }\\ &\quad {}-\frac{rY_{4}}{\varphi \mathcal{H}_{4}} \frac{YE_{4}}{Y_{4}E}+\vartheta _{3}S_{4}Y_{4}+ \frac{rY_{4}}{\varphi \mathcal{H}_{4}}\\ &\quad {}- \biggl( \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{5}}+ \frac{rY_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\frac{E(t-\boldsymbol{\ell })Y_{4}}{E_{4}Y}\,d\boldsymbol{\ell }\\ &\quad {}+\vartheta _{3}S_{4}Y_{4}+\frac{rY_{4}}{\varphi \mathcal{H}_{4}}- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I} \\ & \quad{} +\frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \biggl( \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{5}}+ \frac{rY_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{a ( \lambda +\gamma ) }{\mathcal{P}} \biggl\{ \frac{\mathcal{P}S_{4} ( \varepsilon \vartheta _{2}+b\vartheta _{1}\mathcal{H}_{6} ) }{a\varepsilon ( \lambda +\gamma ) }-1 \biggr\} I \biggr] . \end{aligned}$$
Using the equalities given by (11) in case of \(m=4\), we get
$$\begin{aligned} \frac{d\Phi _{4}}{dt} & =-\mathcal{P} \biggl[ \varrho \frac{ ( S-S_{4} ) ^{2}}{S}+ \vartheta _{3}S_{4}Y_{4} \biggl\{ \frac{S_{4}}{S}-1-\ln \biggl( \frac{S_{4}}{S} \biggr) \biggr\} + \frac{rY_{4}}{\varphi \mathcal{H}_{4}} \biggl\{ \frac{YE_{4}}{Y_{4}E}-1- \ln \biggl( \frac{YE_{4}}{Y_{4}E} \biggr) \biggr\} \\ & \quad{} +\frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \biggl\{ \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{4}}{S_{4}Y_{4}E}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{4}}{S_{4}Y_{4}E} \biggr) \biggr\} \,d\boldsymbol{\ell } \\ & \quad{} + \biggl( \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{5}}+\frac{rY_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl\{ \frac{E(t-\boldsymbol{\ell })Y_{4}}{E_{4}Y}-1-\ln \biggl( \frac{E(t-\boldsymbol{\ell })Y_{4}}{E_{4}Y} \biggr) \biggr\} \,d \boldsymbol{\ell } \\ & \quad{} +\frac{a ( \lambda +\gamma ) }{\mathcal{P}} \biggl\{ \frac{\mathcal{P}S_{4} ( \varepsilon \vartheta _{2}+b\vartheta _{1}\mathcal{H}_{6} ) }{a\varepsilon ( \lambda +\gamma ) }-1 \biggr\} I- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I} \biggr] . \end{aligned}$$
(22)
Therefore, Eq. (22) becomes
$$\begin{aligned} \frac{d\Phi _{4}}{dt} & =-\mathcal{P} \biggl[ \varrho \frac{ ( S-S_{4} ) ^{2}}{S}+ \frac{rY_{4}}{\varphi \mathcal{H}_{4}} \digamma \biggl( \frac{YE_{4}}{Y_{4}E} \biggr) \\ &\quad {}+ \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl\{ \digamma \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{4}}{S_{4}Y_{4}E} \biggr)+\digamma \biggl( \frac{S_{4}}{S} \biggr) \biggr\} \,d \boldsymbol{\ell } \\ & \quad{}+ \biggl( \frac{\vartheta _{3}S_{4}Y_{4}}{\mathcal{H}_{5}}+\frac{rY_{4}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \digamma \biggl( \frac{E(t-\boldsymbol{\ell })Y_{4}}{E_{4}Y} \biggr) \,d \boldsymbol{ \ell } \\ & \quad{} +\frac{a ( \lambda +\gamma ) }{\mathcal{P}} ( \Re _{6}-1 ) I- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}\mathcal{P}}C^{I} \biggr] . \end{aligned}$$
Hence, if \(\Re _{6}\leq 1\), then \(\frac{d\Phi _{4}}{dt}\leq 0\) for all \(S,I,E,Y,V,C^{I}>0\), where \(\frac{d\Phi _{4}}{dt}=0\) occurs at \(S=S_{4}\), \(E=E_{4}\), \(Y=Y_{4}\), and \(I=C^{I}=0\). The trajectories of system (5) converge to \(\Upsilon _{4}^{{\prime }}\) which includes elements with \(S(t)=S_{4}\), \(E(t)=E_{4}\), \(Y(t)=Y_{4}\), and then \(\frac{dS(t)}{dt}=\frac{dY(t)}{dt}=0\). The first and fifth equations of system (5) become
$$\begin{aligned} &0 =\frac{dS(t)}{dt}=\eta -\varrho S_{4}-\vartheta _{1}S_{4}V(t)- \vartheta _{3}S_{4}Y_{4}, \\ &0 =\frac{dY(t)}{dt}=\psi \mathcal{H}_{5}E_{4}-\delta Y_{4}-\mu _{2}C^{Y}(t)Y_{4}, \end{aligned}$$
which imply that \(V(t)=0\) and \(C^{Y}(t)=C_{4}^{Y}\) for all t. Moreover, we have \(\frac{dI(t)}{dt}=0\), then the third equation of system (5) becomes
$$ 0=\frac{dI(t)}{dt}=\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }, $$
which yields \(L(t)=0\) for all t, and then  . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 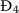 is GAS. □
is GAS. □
Theorem 6
If \(\Re _{5}>1\), \(\Re _{8}\leq 1\), and \(\Re _{1}/\Re _{2}>1\), then  is GAS.
is GAS.
Proof
Define
$$\begin{aligned} \Phi _{5} & =\mathcal{P}S_{5}\digamma \biggl( \frac{S}{S_{5}} \biggr) + \lambda \mathcal{H}_{3}L_{5} \digamma \biggl( \frac{L}{L_{5}} \biggr) + ( \gamma +\lambda ) I_{5}\digamma \biggl( \frac{I}{I_{5}} \biggr) + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E_{5} \digamma \biggl( \frac{E}{E_{5}} \biggr) \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{5}\digamma \biggl( \frac{Y}{Y_{5}} \biggr) + \frac{\mathcal{P}\vartheta _{1}S_{5}}{\varepsilon }V_{5}\digamma \biggl( \frac{V}{V_{5}} \biggr) + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C_{5}^{I} \digamma \biggl( \frac{C^{I}}{C_{5}^{I}} \biggr) \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}+\vartheta _{1} \lambda \mathcal{H}_{3} ( 1-\beta ) S_{5}V_{5} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{5}V_{5}} \biggr) \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{5}I_{5}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{5}I_{5}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+\vartheta _{1}\beta ( \gamma + \lambda ) S_{5}V_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{5}V_{5}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{2}\beta ( \gamma + \lambda ) S_{5}I_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{5}I_{5}} \biggr) \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{5} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{L(\varkappa )}{L_{5}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )Y(\varkappa )}{S_{5}Y_{5}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{E(\varkappa )}{E_{5}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{5}I_{5}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{I(\varkappa )}{I_{5}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }. \end{aligned}$$
Calculate \(\frac{d\Phi _{5}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{5}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{5}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) +\lambda \mathcal{H}_{3} \biggl( 1- \frac{L_{5}}{L} \biggr) \\ &\quad{}\times \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad {} + ( \gamma +\lambda ) \biggl( 1- \frac{I_{5}}{I} \biggr) \biggl[ \beta \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ &\quad {}+\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-aI-\mu _{1}C^{I}I \biggr] \\ &\quad{}+\frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl( 1- \frac{E_{5}}{E} \biggr) \biggl[ \varphi \vartheta _{3} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t- \boldsymbol{\ell })\,d\boldsymbol{ \ell }+rY- ( \psi +\omega ) E \biggr] \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1-\frac{Y_{5}}{Y} \biggr) \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}(\boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d \boldsymbol{ \ell }-\delta Y-\mu _{2}C^{Y}Y \biggr] \\ &\quad {}+ \frac{\mathcal{P}\vartheta _{1}S_{5}}{\varepsilon } \biggl( 1-\frac{V_{5}}{V} \biggr) \biggl[ b \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) I(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] \\ & \quad{} + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \biggl( 1- \frac{C_{5}^{I}}{C^{I}} \biggr) \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \bigl( \sigma _{2}C^{Y}Y- \pi _{2}C^{Y} \bigr) \\ &\quad{}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{5}V_{5} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{5}V_{5}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{5}V_{5}}+\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{5}I_{5} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{5}I_{5}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{5}I_{5}}+\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{1}\beta ( \gamma +\lambda ) S_{5}V_{5} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{5}V_{5}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{5}V_{5}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\beta ( \gamma +\lambda ) S_{5}I_{5} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{5}I_{5}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{5}I_{5}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{5} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L}{L_{5}}- \frac{L(t-\boldsymbol{\ell })}{L_{5}}+\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{SY}{S_{5}Y_{5}}- \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{S_{5}Y_{5}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E}{E_{5}}- \frac{E(t-\boldsymbol{\ell })}{E_{5}}+\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}+\frac{b\mathcal{P}\vartheta _{1}S_{5}I_{5}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \biggl[ \frac{I}{I_{5}}- \frac{I(t-\boldsymbol{\ell })}{I_{5}}+\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \biggr] \,d\boldsymbol{ \ell }. \end{aligned}$$
(23)
Summing the terms of Eq. (23), we get
$$\begin{aligned} \frac{d\Phi _{5}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{5}}{S} \biggr) ( \eta -\varrho S ) +\mathcal{P}\vartheta _{2}S_{5}I+ \mathcal{P}\vartheta _{3}S_{5}Y-\vartheta _{1}\lambda \mathcal{H}_{3} ( 1- \beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \\ &\quad{}\times \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{5}}{L}\,d \boldsymbol{\ell }-\vartheta _{2} \lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{5}}{L}\,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( \lambda +\gamma ) L_{5}-a ( \lambda +\gamma ) I-\vartheta _{1}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{5}}{I}\,d\boldsymbol{\ell } \\ &\quad{}-\vartheta _{2}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })I_{5}}{I}\,d\boldsymbol{\ell }\\ &\quad {}- \lambda ( \lambda +\gamma ) \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\frac{L(t-\boldsymbol{\ell })I_{5}}{I}\,d\boldsymbol{\ell }+a ( \lambda +\gamma ) I_{5}+\mu _{1} ( \lambda + \gamma ) C^{I}I_{5} \\ &\quad{}+ \frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}Y- \frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{5}}{E}\,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}\frac{YE_{5}}{E}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}}E_{5}- \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y\\ &\quad {}- \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \frac{E(t-\boldsymbol{\ell })Y_{5}}{Y}\,d\boldsymbol{\ell }+ \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{5} \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y_{5}- \frac{b\mathcal{P}\vartheta _{1}S_{5}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \frac{I(t-\boldsymbol{\ell })V_{5}}{V}\,d\boldsymbol{\ell }+\mathcal{P}\vartheta _{1}S_{5}V_{5} \\ &\quad{}- \frac{\mu _{1}\pi _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I}-\mu _{1} ( \lambda +\gamma ) C_{5}^{I}I+ \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C_{5}^{I}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y} \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{5}V_{5}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{5}I_{5}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{5}V_{5}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda ( \gamma +\lambda ) L_{5} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P} ( \psi +\omega ) E_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{b\mathcal{P}\vartheta _{1}S_{5}\mathcal{H}_{6}}{\varepsilon }I+\frac{b\mathcal{P}\vartheta _{1}S_{5}I_{5}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the steady state conditions for 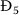
$$\begin{aligned} & \eta =\varrho S_{5}+\vartheta _{1}S_{5}V_{5}+ \vartheta _{2}S_{5}I_{5}+\vartheta _{3}S_{5}Y_{5}, \qquad \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5} ) = ( \lambda +\gamma ) L_{5}, \\ & \beta \mathcal{H}_{2} ( \vartheta _{1}S_{5}V_{5}+ \vartheta _{2}S_{5}I_{5} ) +\lambda \mathcal{H}_{3}L_{5}= \bigl( a+\mu _{1}C_{5}^{I} \bigr) I_{5} \qquad I_{5}= \frac{\pi _{1}}{\sigma _{1}}, \qquad V_{5}= \frac{b\mathcal{H}_{6}}{\varepsilon }I_{5}, \\ & \vartheta _{3}S_{5}Y_{5}+ \frac{rY_{5}}{\varphi \mathcal{H}_{4}}=\frac{ ( \psi +\omega ) E_{5}}{\varphi \mathcal{H}_{4}}= \frac{\delta ( \psi +\omega ) Y_{5}}{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}, \end{aligned}$$
we obtain
$$ \mathcal{P} ( \vartheta _{1}S_{5}V_{5}+ \vartheta _{2}S_{5}I_{5} ) = ( \lambda +\gamma ) \bigl( a+\mu _{1}C_{5}^{I} \bigr) I_{5}. $$
Moreover, we get
$$\begin{aligned} \frac{d\Phi _{5}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{5}}{S} \biggr) ( \varrho S_{5}-\varrho S ) +\mathcal{P} ( \vartheta _{1}S_{5}V_{5}+ \vartheta _{2}S_{5}I_{5}+\vartheta _{3}S_{5}Y_{5} ) \biggl( 1-\frac{S_{5}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{5}V_{5}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{5}}{S_{5}V_{5}L}\,d \boldsymbol{\ell }\\ &\quad {} -\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{5}}{S_{5}I_{5}L}\,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{1}\mathcal{H}_{3} ( 1-\beta ) ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5} ) \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{5}V_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{5}}{S_{5}V_{5}I}\,d \boldsymbol{\ell }\\ &\quad {}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{5}I}\,d\boldsymbol{\ell }\\ &\quad {}- \lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{5}V_{5}+ \vartheta _{2}S_{5}I_{5} ) \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\frac{L(t-\boldsymbol{\ell })I_{5}}{L_{5}I}\,d\boldsymbol{\ell }\\ &\quad {}+\mathcal{P} ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5} ) - \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{5}}{S_{5}Y_{5}E}\,d\boldsymbol{\ell }\\ &\quad {}-\frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}} \frac{YE_{5}}{Y_{5}E}+\mathcal{P}\vartheta _{3}S_{5}Y_{5}+ \frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}} \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{5}}+\frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\frac{E(t-\boldsymbol{\ell })Y_{5}}{E_{5}Y}\,d\boldsymbol{\ell }+ \mathcal{P}\vartheta _{3}S_{5}Y_{5}+\frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}} \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{5}V_{5}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \frac{I(t-\boldsymbol{\ell })V_{5}}{I_{5}V}\,d\boldsymbol{\ell }+\mathcal{P} \vartheta _{1}S_{5}V_{5}\\ &\quad {}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{5}V_{5} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{5}V_{5}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{5}V_{5}+ \vartheta _{2}S_{5}I_{5} ) \int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+ \biggl( \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{5}}+ \frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{5}V_{5}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( Y_{5}-\frac{\pi _{2}}{\sigma _{2}} \biggr) C^{Y}. \end{aligned}$$
Using the equalities given by (10) and (11) in case of \(n=m=5\), we get
$$\begin{aligned} \frac{d\Phi _{5}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{5})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5}+\vartheta _{3}S_{5}Y_{5} ) \biggl[ \frac{S_{5}}{S}-1- \ln \biggl( \frac{S_{5}}{S} \biggr) \biggr] \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{5}V_{5} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{5}}{S_{5}V_{5}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{5}}{S_{5}V_{5}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{5}I_{5} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{5}}{S_{5}I_{5}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{5}}{S_{5}I_{5}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{5}V_{5} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{5}}{S_{5}V_{5}I}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{5}}{S_{5}V_{5}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{5}I}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{5}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5} ) \\ &\quad {}\times\int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L(t-\boldsymbol{\ell })I_{5}}{L_{5}I}-1-\ln \biggl( \frac{L(t-\boldsymbol{\ell })I_{5}}{L_{5}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}} \biggl[ \frac{YE_{5}}{Y_{5}E}-1-\ln \biggl( \frac{YE_{5}}{Y_{5}E} \biggr) \biggr] \\ & \quad{}- \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{5}}{S_{5}Y_{5}E}-1 -\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{5}}{S_{5}Y_{5}E} \biggr) \biggr] \,d\boldsymbol{\ell } \\ & \quad{} - \biggl( \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{5}}+ \frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{ \kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E(t-\boldsymbol{\ell })Y_{5}}{E_{5}Y}-1-\ln \biggl( \frac{E(t-\boldsymbol{\ell })Y_{5}}{E_{5}Y} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad {}- \frac{\mathcal{P}\vartheta _{1}S_{5}V_{5}}{\mathcal{H}_{6}}\int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \biggl[ \frac{I(t-\boldsymbol{\ell })V_{5}}{I_{5}V}-1-\ln \biggl( \frac{I(t-\boldsymbol{\ell })V_{5}}{I_{5}V} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( Y_{5}-\frac{\pi _{2}}{\sigma _{2}} \biggr) C^{Y}. \end{aligned}$$
(24)
Therefore, Eq. (24) becomes
$$\begin{aligned} \frac{d\Phi _{5}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{5})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5}+\vartheta _{3}S_{5}Y_{5} ) \digamma \biggl( \frac{S_{5}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{5}V_{5}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{5}}{S_{5}V_{5}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{5}I_{5}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{5}}{S_{5}I_{5}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{5}V_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{5}}{S_{5}V_{5}I} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{5}I_{5} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{5}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\digamma \biggl( \frac{L(t-\boldsymbol{\ell })I_{5}}{L_{5}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}}\digamma \biggl( \frac{YE_{5}}{Y_{5}E} \biggr) - \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })\digamma \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{5}}{S_{5}Y_{5}E} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{5}Y_{5}}{\mathcal{H}_{5}}+\frac{\mathcal{P}rY_{5}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\digamma \biggl( \frac{E(t-\boldsymbol{\ell })Y_{5}}{E_{5}Y} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{5}V_{5}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \digamma \biggl( \frac{I(t-\boldsymbol{\ell })V_{5}}{I_{5}V} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) [ \pi _{1}\sigma _{2} ( b\vartheta _{1}\mathcal{H}_{6}+\varepsilon \vartheta _{2} ) +\varepsilon \sigma _{1} ( \pi _{2}\vartheta _{3}+\varrho \sigma _{2} ) ] }{\varphi \psi \vartheta _{3}\varepsilon \sigma _{1}\sigma _{2}\mathcal{H}_{4}\mathcal{H}_{5}} ( \Re _{8}-1 ) C^{Y}. \end{aligned}$$
Hence, if \(\Re _{8}\leq 1\), then \(\frac{d\Phi _{5}}{dt}\leq 0\) for all \(S,L,I,E,Y,V,C^{Y}>0\). One can show that \(\frac{d\Phi _{5}}{dt}=0\) when \((S,L,I,E,Y,V,C^{Y})=(S_{5},L_{5},I_{5},E_{5},Y_{5},V_{5},0)\). The solutions of model (5) tend to \(\Upsilon _{5}^{{\prime }}\) which includes elements with \((S(t),L(t),I(t),V(t))=(S_{5},L_{5},I_{5},V_{5})\), and then \(\frac{dI(t)}{dt}=0\). The third equation of system (5) becomes
$$ 0=\frac{dI(t)}{dt}=\beta \mathcal{H}_{2} ( \vartheta _{1}S_{5}V_{5}+\vartheta _{2}S_{5}I_{5} ) +\lambda \mathcal{H}_{3}L_{5}-aI_{5}- \mu _{1}C^{I}(t)I_{5}, $$
which yields \(C^{I}(t)=C_{5}^{I}\) for all t, and hence  . Applying LLAS theorem, we get
. Applying LLAS theorem, we get  is GAS. □
is GAS. □
Theorem 7
If \(\Re _{6}>1\), \(\Re _{7}\leq 1\), and \(\Re _{2}/\Re _{1}>1\), then  is GAS.
is GAS.
Proof
Define
$$\begin{aligned} \Phi _{6} & =\mathcal{P}S_{6}\digamma \biggl( \frac{S}{S_{6}} \biggr) + \lambda \mathcal{H}_{3}L_{6} \digamma \biggl( \frac{L}{L_{6}} \biggr) + ( \gamma +\lambda ) I_{6}\digamma \biggl( \frac{I}{I_{6}} \biggr) + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E_{6} \digamma \biggl( \frac{E}{E_{6}} \biggr) \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{6}\digamma \biggl( \frac{Y}{Y_{6}} \biggr) + \frac{\mathcal{P}\vartheta _{1}S_{6}}{\varepsilon }V_{6}\digamma \biggl( \frac{V}{V_{6}} \biggr) + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C^{I} \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{6}^{Y}\digamma \biggl( \frac{C^{Y}}{C_{6}^{Y}} \biggr) \\ &\quad {}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{6}V_{6} \int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{6}V_{6}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{6}I_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{6}I_{6}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+\vartheta _{1}\beta ( \gamma + \lambda ) S_{6}V_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{6}V_{6}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{2}\beta ( \gamma + \lambda ) S_{6}I_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{6}I_{6}} \biggr) \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{6} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{L(\varkappa )}{L_{6}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )Y(\varkappa )}{S_{6}Y_{6}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{E(\varkappa )}{E_{6}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{6}I_{6}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{I(\varkappa )}{I_{6}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }. \end{aligned}$$
Calculate \(\frac{d\Phi _{6}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{6}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{6}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) +\lambda \mathcal{H}_{3} \biggl( 1- \frac{L_{6}}{L} \biggr) \\ &\quad{}\times \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad {} + ( \gamma +\lambda ) \biggl( 1- \frac{I_{6}}{I} \biggr)\biggl[ \beta \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-aI-\mu _{1}C^{I}I \biggr] \\ &\quad{}+\frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl( 1- \frac{E_{6}}{E} \biggr) \biggl[ \varphi \vartheta _{3} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t- \boldsymbol{\ell })\,d\boldsymbol{ \ell }+rY- ( \psi +\omega ) E \biggr] \\ &\quad {} + \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}\biggl( 1-\frac{Y_{6}}{Y} \biggr) \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}(\boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d \boldsymbol{ \ell }-\delta Y-\mu _{2}C^{Y}Y \biggr] \\ &\quad{} + \frac{\mathcal{P}\vartheta _{1}S_{6}}{\varepsilon } \biggl( 1-\frac{V_{6}}{V} \biggr)\biggl[ b \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] \\ &\quad{}+ \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1- \frac{C_{6}^{Y}}{C^{Y}} \biggr)\bigl( \sigma _{2}C^{Y}Y-\pi _{2}C^{Y} \bigr) \\ &\quad{} +\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{6}V_{6} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}(\boldsymbol{\ell }) \biggl[ \frac{SV}{S_{6}V_{6}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{6}V_{6}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{6}I_{6} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{6}I_{6}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{6}I_{6}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\vartheta _{1}\beta ( \gamma +\lambda ) S_{6}V_{6} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{6}V_{6}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{6}V_{6}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\vartheta _{2}\beta ( \gamma +\lambda ) S_{6}I_{6} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{6}I_{6}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{6}I_{6}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\lambda ( \gamma +\lambda ) L_{6}\int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L}{L_{6}}-\frac{L(t-\boldsymbol{\ell })}{L_{6}}+\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{SY}{S_{6}Y_{6}}- \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{S_{6}Y_{6}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E}{E_{6}}- \frac{E(t-\boldsymbol{\ell })}{E_{6}}+\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}+\frac{b\mathcal{P}\vartheta _{1}S_{6}I_{6}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \biggl[ \frac{I}{I_{6}}- \frac{I(t-\boldsymbol{\ell })}{I_{6}}+\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \biggr] \,d\boldsymbol{ \ell }. \end{aligned}$$
(25)
Collecting the terms of Eq. (25), we obtain
$$\begin{aligned} \frac{d\Phi _{6}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{6}}{S} \biggr) ( \eta -\varrho S ) +\mathcal{P}\vartheta _{2}S_{6}I+ \mathcal{P}\vartheta _{3}S_{6}Y-\vartheta _{1}\lambda \mathcal{H}_{3} ( 1- \beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \\ &\quad{}\times \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{6}}{L}\,d \boldsymbol{\ell }-\vartheta _{2} \lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{6}}{L}\,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( \lambda +\gamma ) L_{6}-a ( \lambda +\gamma ) I-\vartheta _{1}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{6}}{I}\,d\boldsymbol{\ell } \\ &\quad{}-\vartheta _{2}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })I_{6}}{I}\,d\boldsymbol{\ell }\\ &\quad {}- \lambda ( \lambda +\gamma ) \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\frac{L(t-\boldsymbol{\ell })I_{6}}{I}\,d\boldsymbol{\ell }+a ( \lambda +\gamma ) I_{6}+\mu _{1} ( \lambda + \gamma ) C^{I}I_{6} \\ &\quad{}+ \frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}Y- \frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{6}}{E}\,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}\frac{YE_{6}}{E}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}}E_{6}- \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y\\ &\quad {}- \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \frac{E(t-\boldsymbol{\ell })Y_{6}}{Y}\,d\boldsymbol{\ell }+ \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{6} + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y_{6}\\ &\quad{}- \frac{b\mathcal{P}\vartheta _{1}S_{6}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \frac{I(t-\boldsymbol{\ell })V_{6}}{V}\,d\boldsymbol{\ell }+\mathcal{P}\vartheta _{1}S_{6}V_{6}- \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C^{I} \\ &\quad{}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}- \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{6}^{Y}Y+ \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{6}^{Y} \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{6}V_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{6}I_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d\boldsymbol{\ell } \\ &\quad{} +\beta ( \gamma +\lambda ) \vartheta _{1}S_{6}V_{6}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{6}I_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda ( \gamma +\lambda ) L_{6} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P} ( \psi +\omega ) E_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{6}\mathcal{H}_{6}}{\varepsilon }I+ \frac{b\mathcal{P}\vartheta _{1}S_{6}I_{6}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the steady state conditions for 
$$\begin{aligned} & \eta =\varrho S_{6}+\vartheta _{1}S_{6}V_{6}+ \vartheta _{2}S_{6}I_{6}+\vartheta _{3}S_{6}Y_{6}, \qquad \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6} ) = ( \lambda +\gamma ) L_{6}, \\ & \beta \mathcal{H}_{2} ( \vartheta _{1}S_{6}V_{6}+ \vartheta _{2}S_{6}I_{6} ) +\lambda \mathcal{H}_{3}L_{6}=aI_{6}, \qquad Y_{6}=\frac{\pi _{2}}{\sigma _{2}}, \qquad V_{6}= \frac{b\mathcal{H}_{6}I_{6}}{\varepsilon }, \\ & \vartheta _{3}S_{6}Y_{6}+ \frac{rY_{6}}{\varphi \mathcal{H}_{4}}=\frac{ ( \psi +\omega ) E_{6}}{\varphi \mathcal{H}_{4}}= \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{6}+ \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{6}^{Y}Y_{6}, \end{aligned}$$
we get
$$ \mathcal{P} ( \vartheta _{1}S_{6}V_{6}+ \vartheta _{2}S_{6}I_{6} ) =a ( \lambda +\gamma ) I_{6}. $$
Moreover, we get
$$\begin{aligned} \frac{d\Phi _{6}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{6}}{S} \biggr) ( \varrho S_{6}-\varrho S ) +\mathcal{P} ( \vartheta _{1}S_{6}V_{6}+ \vartheta _{2}S_{6}I_{6}+\vartheta _{3}S_{6}Y_{6} ) \biggl( 1-\frac{S_{6}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{6}V_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{6}}{S_{6}V_{6}L}\,d \boldsymbol{\ell }-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{6}I_{6} \\ &\quad{}\times \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{6}}{S_{6}I_{6}L}\,d \boldsymbol{\ell }+\lambda \mathcal{H}_{1}\mathcal{H}_{3} ( 1-\beta ) ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6} ) \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{6}V_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{6}}{S_{6}V_{6}I}\,d \boldsymbol{\ell }\\ &\quad {}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{6}I_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{6}I}\,d \boldsymbol{\ell }\\ &\quad {}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{6}V_{6}+ \vartheta _{2}S_{6}I_{6} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \frac{L(t-\boldsymbol{\ell })I_{6}}{L_{6}I}\,d\boldsymbol{\ell } \\ &\quad{}+\mathcal{P} ( \vartheta _{1}S_{6}V_{6}+ \vartheta _{2}S_{6}I_{6} ) -\frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{6}}{S_{6}Y_{6}E}\,d \boldsymbol{\ell }\\ &\quad {}-\frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}}\frac{YE_{6}}{Y_{6}E}+\mathcal{P}\vartheta _{3}S_{6}Y_{6}+ \frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}} \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{5}}+ \frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\frac{E(t-\boldsymbol{\ell })Y_{6}}{E_{6}Y}\,d \boldsymbol{\ell } \\ &\quad{}+\mathcal{P}\vartheta _{3}S_{6}Y_{6}+ \frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}}- \frac{\mathcal{P}\vartheta _{1}S_{6}V_{6}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\frac{I(t-\boldsymbol{\ell })V_{6}}{I_{6}V}\,d\boldsymbol{\ell }+\mathcal{P} \vartheta _{1}S_{6}V_{6} \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{6}V_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{6}I_{6} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{6}V_{6}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{6}I_{6}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+ \biggl( \frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{5}}+ \frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{6}V_{6}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }+\mu _{1} ( \lambda +\gamma ) \biggl( I_{6}- \frac{\pi _{1}}{\sigma _{1}} \biggr) C^{I}. \end{aligned}$$
Using the equalities given by (10) and (11) in case of \(n=m=6\), we get
$$\begin{aligned} \frac{d\Phi _{6}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{6})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6}+\vartheta _{3}S_{6}Y_{6} ) \biggl[ \frac{S_{6}}{S}-1- \ln \biggl( \frac{S_{6}}{S} \biggr) \biggr] \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{6}V_{6} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{6}}{S_{6}V_{6}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{6}}{S_{6}V_{6}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{6}I_{6} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{6}}{S_{6}I_{6}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{6}}{S_{6}I_{6}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{6}V_{6} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{6}}{S_{6}V_{6}I}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{6}}{S_{6}V_{6}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{6}I_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{6}I}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{6}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6} ) \\ &\quad {}\times\int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })) \biggl[ \frac{L(t-\boldsymbol{\ell })I_{6}}{L_{6}I}-1-\ln \biggl( \frac{L(t-\boldsymbol{\ell })I_{6}}{L_{6}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{6}}{S_{6}Y_{6}E}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{6}}{S_{6}Y_{6}E} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}} \biggl[ \frac{YE_{6}}{Y_{6}E}-1-\ln \biggl( \frac{YE_{6}}{Y_{6}E} \biggr) \biggr] \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{5}}+\frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E(t-\boldsymbol{\ell })Y_{6}}{E_{6}Y}-1-\ln \biggl( \frac{E(t-\boldsymbol{\ell })Y_{6}}{E_{6}Y} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{6}V_{6}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \biggl[ \frac{I(t-\boldsymbol{\ell })V_{6}}{I_{6}V}-1-\ln \biggl( \frac{I(t-\boldsymbol{\ell })V_{6}}{I_{6}V} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad {}+\mu _{1} ( \lambda +\gamma ) \biggl( I_{6}- \frac{\pi _{1}}{\sigma _{1}} \biggr) C^{I}. \end{aligned}$$
(26)
Therefore, Eq. (26) becomes
$$\begin{aligned} \frac{d\Phi _{6}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{6})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6}+\vartheta _{3}S_{6}Y_{6} ) +\digamma \biggl( \frac{S_{6}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{6}V_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{6}}{S_{6}V_{6}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{6}I_{6}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{6}}{S_{6}I_{6}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{6}V_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{6}}{S_{6}V_{6}I} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{6}I_{6} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{6}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{6}V_{6}+\vartheta _{2}S_{6}I_{6} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }))\digamma \biggl( \frac{L(t-\boldsymbol{\ell })I_{6}}{L_{6}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{6}}{S_{6}Y_{6}E} \biggr) \,d \boldsymbol{ \ell }-\frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}} \digamma \biggl( \frac{YE_{6}}{Y_{6}E} \biggr) \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{6}Y_{6}}{\mathcal{H}_{5}}+\frac{\mathcal{P}rY_{6}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\digamma \biggl( \frac{E(t-\boldsymbol{\ell })Y_{6}}{E_{6}Y} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{6}V_{6}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \digamma \biggl( \frac{I(t-\boldsymbol{\ell })V_{6}}{I_{6}V} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}+ \frac{\mu _{1} ( \gamma +\lambda ) [ \pi _{1}\sigma _{2} ( b\vartheta _{1}\mathcal{H}_{6}+\varepsilon \vartheta _{2} ) +\varepsilon \sigma _{1} ( \pi _{2}\vartheta _{3}+\varrho \sigma _{2} ) ] }{\sigma _{1}\sigma _{2} ( b\vartheta _{1}\mathcal{H}_{6}+\varepsilon \vartheta _{2} ) } ( \Re _{7}-1 ) C^{I}. \end{aligned}$$
Hence, if \(\Re _{7}\leq 1\), then \(\frac{d\Phi _{6}}{dt}\leq 0\) for all \(S,L,I,E,Y,V,C^{I}>0\). Similar to the previous theorems, one can show that \(\frac{d\Phi _{6}}{dt}=0\) at \((S,L,I,E,Y,V,C^{I})=(S_{6},L_{6},I_{6},E_{6},Y_{6},V_{6},0)\). The solutions of system (5) reach \(\Upsilon _{6}^{{\prime }}\) which contains elements with \(E(t)=E_{6}\), \(Y(t)=Y_{6}\), and then \(\frac{dY(t)}{dt}=0\). The fifth equation of system (5) becomes
$$ 0=\frac{dY(t)}{dt}=\psi \mathcal{H}_{5}E_{6}-\delta Y_{6}-\mu _{2}C^{Y}(t)Y_{6}, $$
which yields \(C^{Y}(t)=C_{6}^{Y}\) for all t, and hence 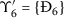 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 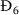 is GAS. □
is GAS. □
Theorem 8
If \(\Re _{7}>1\) and \(\Re _{8}>1\), then  is GAS.
is GAS.
Proof
Consider
$$\begin{aligned} \Phi _{7} & =\mathcal{P}S_{7}\digamma \biggl( \frac{S}{S_{7}} \biggr) + \lambda \mathcal{H}_{3}L_{7} \digamma \biggl( \frac{L}{L_{7}} \biggr) + ( \gamma +\lambda ) I_{7}\digamma \biggl( \frac{I}{I_{7}} \biggr) + \frac{\mathcal{P}}{\varphi \mathcal{H}_{4}}E_{7} \digamma \biggl( \frac{E}{E_{7}} \biggr) \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{7}\digamma \biggl( \frac{Y}{Y_{7}} \biggr) + \frac{\mathcal{P}\vartheta _{1}S_{7}}{\varepsilon }V_{7}\digamma \biggl( \frac{V}{V_{7}} \biggr) + \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}}C_{7}^{I} \digamma \biggl( \frac{C^{I}}{C_{7}^{I}} \biggr) \\ &\quad{}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{7}^{Y}\digamma \biggl( \frac{C^{Y}}{C_{7}^{Y}} \biggr)\\ &\quad {} +\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{7}V_{7} \int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{7}V_{7}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{7}I_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{7}I_{7}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{1}\beta ( \gamma + \lambda ) S_{7}V_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )V(\varkappa )}{S_{7}V_{7}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+\vartheta _{2}\beta ( \gamma + \lambda ) S_{7}I_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )I(\varkappa )}{S_{7}I_{7}} \biggr) \,d\varkappa \,d\boldsymbol{\ell } \\ &\quad{}+\lambda ( \gamma +\lambda ) L_{7} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{L(\varkappa )}{L_{7}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{S(\varkappa )Y(\varkappa )}{S_{7}Y_{7}} \biggr) \,d\varkappa \,d \boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{E(\varkappa )}{E_{7}} \biggr) \,d\varkappa \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{7}I_{7}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \int _{t-\boldsymbol{\ell }}^{t}\digamma \biggl( \frac{I(\varkappa )}{I_{7}} \biggr) \,d\varkappa \,d \boldsymbol{\ell }. \end{aligned}$$
Calculate \(\frac{d\Phi _{7}}{dt}\) as follows:
$$\begin{aligned} \frac{d\Phi _{7}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{7}}{S} \biggr) ( \eta -\varrho S-\vartheta _{1}SV-\vartheta _{2}SI-\vartheta _{3}SY ) +\lambda \mathcal{H}_{3} \biggl( 1- \frac{L_{7}}{L} \biggr) \\ &\quad{}\times \biggl[ ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell }- ( \lambda +\gamma ) L \biggr] \\ &\quad {} + ( \gamma +\lambda ) \biggl( 1- \frac{I_{7}}{I} \biggr) \biggl[ \beta \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell })S(t-\boldsymbol{\ell }) \bigl\{ \vartheta _{1}V(t- \boldsymbol{\ell })+\vartheta _{2}I(t-\boldsymbol{\ell }) \bigr\} \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })L(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-aI-\mu _{1}C^{I}I \biggr] \\ &\quad{}+\frac{\mathcal{P}}{\varphi \mathcal{H}_{4}} \biggl( 1- \frac{E_{7}}{E} \biggr) \biggl[ \varphi \vartheta _{3} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell })S(t-\boldsymbol{\ell })Y(t- \boldsymbol{\ell })\,d\boldsymbol{ \ell }+rY- ( \psi +\omega ) E \biggr] \\ &\quad {}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1-\frac{Y_{7}}{Y} \biggr) \biggl[ \psi \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}(\boldsymbol{\ell })E(t-\boldsymbol{\ell })\,d \boldsymbol{ \ell }-\delta Y-\mu _{2}C^{Y}Y \biggr] \\ &\quad {} + \frac{\mathcal{P}\vartheta _{1}S_{7}}{\varepsilon } \biggl( 1-\frac{V_{7}}{V} \biggr) \biggl[ b \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })I(t-\boldsymbol{\ell })\,d\boldsymbol{\ell }-\varepsilon V \biggr] \\ &\quad {}+ \frac{\mu _{1} ( \gamma +\lambda ) }{\sigma _{1}} \biggl( 1- \frac{C_{7}^{I}}{C^{I}} \biggr) \bigl( \sigma _{1}C^{I}I-\pi _{1}C^{I} \bigr) \\ &\quad {} + \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}} \biggl( 1-\frac{C_{7}^{Y}}{C^{Y}} \biggr) \bigl( \sigma _{2}C^{Y}Y-\pi _{2}C^{Y} \bigr) \\ &\quad {}+\vartheta _{1}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{7}V_{7} \\ &\quad {}\times\int _{0}^{\kappa _{1}} \bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{7}V_{7}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{7}V_{7}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\vartheta _{2}\lambda \mathcal{H}_{3} ( 1-\beta ) S_{7}I_{7} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{7}I_{7}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{7}I_{7}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\vartheta _{1}\beta ( \gamma +\lambda ) S_{7}V_{7} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SV}{S_{7}V_{7}}- \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{S_{7}V_{7}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\vartheta _{2}\beta ( \gamma +\lambda ) S_{7}I_{7} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{SI}{S_{7}I_{7}}- \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{7}I_{7}} +\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \biggr] \,d \boldsymbol{ \ell } \\ &\quad {}+\lambda ( \gamma +\lambda ) L_{7}\int _{0}^{\kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \biggl[ \frac{L}{L_{7}}-\frac{L(t-\boldsymbol{\ell })}{L_{7}}+\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{SY}{S_{7}Y_{7}}- \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{S_{7}Y_{7}}+ \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) E_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E}{E_{7}}- \frac{E(t-\boldsymbol{\ell })}{E_{7}}+\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}+\frac{b\mathcal{P}\vartheta _{1}S_{7}I_{7}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \biggl[ \frac{I}{I_{7}}- \frac{I(t-\boldsymbol{\ell })}{I_{7}}+\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \biggr] \,d\boldsymbol{ \ell }. \end{aligned}$$
(27)
Summing the terms of Eq. (27), we get
$$\begin{aligned} \frac{d\Phi _{7}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{7}}{S} \biggr) ( \eta -\varrho S ) +\mathcal{P}\vartheta _{2}S_{7}I+ \mathcal{P}\vartheta _{3}S_{7}Y-\vartheta _{1}\lambda \mathcal{H}_{3} ( 1- \beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \\ &\quad{}\times \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{7}}{L}\,d \boldsymbol{\ell }-\vartheta _{2} \lambda \mathcal{H}_{3} ( 1-\beta ) \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{7}}{L}\,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( \lambda +\gamma ) L_{7}-a ( \lambda +\gamma ) I-\vartheta _{1}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}} \bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{7}}{I}\,d\boldsymbol{\ell } \\ &\quad{}-\vartheta _{2}\beta ( \gamma +\lambda ) \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })I_{7}}{I}\,d\boldsymbol{\ell }\\ &\quad {}- \lambda ( \lambda +\gamma ) \int _{0}^{\kappa _{3}} \bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\frac{L(t-\boldsymbol{\ell })I_{7}}{I}\,d\boldsymbol{\ell }+a ( \lambda +\gamma ) I_{7}+\mu _{1} ( \lambda + \gamma ) C^{I}I_{7} \\ &\quad{}+ \frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}Y- \frac{\mathcal{P}\vartheta _{3}}{\mathcal{H}_{4}} \int _{0}^{ \kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{7}}{E}\,d\boldsymbol{\ell }-\frac{\mathcal{P}r}{\varphi \mathcal{H}_{4}}\frac{YE_{7}}{E} \\ &\quad{}+ \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}}E_{7}- \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y- \frac{\mathcal{P} ( \psi +\omega ) }{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \frac{E(t-\boldsymbol{\ell })Y_{7}}{Y}\,d\boldsymbol{\ell } \\ &\quad{}+ \frac{\mathcal{P}\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{7}+ \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}Y_{7}- \frac{b\mathcal{P}\vartheta _{1}S_{7}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}(\boldsymbol{\ell }) \frac{I(t-\boldsymbol{\ell })V_{7}}{V}\,d\boldsymbol{\ell } \\ &\quad{}+\mathcal{P}\vartheta _{1}S_{7}V_{7}- \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C^{I}-\mu _{1} ( \lambda + \gamma ) C_{7}^{I}I+ \frac{\mu _{1}\pi _{1} ( \lambda +\gamma ) }{\sigma _{1}}C_{7}^{I} \\ &\quad{}- \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C^{Y}- \frac{\mu _{2}\mathcal{P} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{7}^{Y}Y+ \frac{\mu _{2}\pi _{2}\mathcal{P} ( \psi +\omega ) }{\sigma _{2}\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{7}^{Y} \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{7}V_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{7}I_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{7}V_{7}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{7}I_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\lambda ( \gamma +\lambda ) L_{7} \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P} ( \psi +\omega ) E_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell }+ \frac{b\mathcal{P}\vartheta _{1}S_{7}\mathcal{H}_{6}}{\varepsilon }I\\ &\quad {}+ \frac{b\mathcal{P}\vartheta _{1}S_{7}I_{7}}{\varepsilon } \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the steady state conditions for 
$$\begin{aligned} & \eta =\varrho S_{7}+\vartheta _{1}S_{7}V_{7}+ \vartheta _{2}S_{7}I_{7}+\vartheta _{3}S_{7}Y_{7}, \\ &\mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7} ) = ( \lambda +\gamma ) L_{7}, \\ & \beta \mathcal{H}_{2} ( \vartheta _{1}S_{7}V_{7}+ \vartheta _{2}S_{7}I_{7} ) +\lambda \mathcal{H}_{3}L_{7}= \bigl( a+\mu _{1}C_{7}^{I} \bigr) I_{7}, \\ & I_{7}= \frac{\pi _{1}}{\sigma _{1}}, \qquad Y_{7}= \frac{\pi _{2}}{\sigma _{2}}, \qquad V_{7}= \frac{b\mathcal{H}_{6}I_{7}}{\varepsilon }, \\ & \vartheta _{3}S_{7}Y_{7}+ \frac{rY_{7}}{\varphi \mathcal{H}_{4}}=\frac{ ( \psi +\omega ) E_{7}}{\varphi \mathcal{H}_{4}}= \frac{\delta ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}Y_{7}+ \frac{\mu _{2} ( \psi +\omega ) }{\varphi \psi \mathcal{H}_{4}\mathcal{H}_{5}}C_{7}^{Y}Y_{7}, \end{aligned}$$
we get
$$ \mathcal{P} ( \vartheta _{1}S_{7}V_{7}+ \vartheta _{2}S_{7}I_{7} ) = ( \lambda +\gamma ) \bigl( a+\mu _{1}C_{7}^{I} \bigr) I_{7}. $$
Moreover, we get
$$\begin{aligned} \frac{d\Phi _{7}}{dt} & =\mathcal{P} \biggl( 1-\frac{S_{7}}{S} \biggr) ( \varrho S_{7}-\varrho S ) +\mathcal{P} ( \vartheta _{1}S_{7}V_{7}+ \vartheta _{2}S_{7}I_{7}+\vartheta _{3}S_{7}Y_{7} ) \biggl( 1-\frac{S_{7}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{7}V_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{7}}{S_{7}V_{7}L}\,d \boldsymbol{\ell }\\ &\quad {}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{7}I_{7} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{7}}{S_{7}I_{7}L}\,d \boldsymbol{\ell }\\ &\quad {}+\lambda \mathcal{H}_{1}\mathcal{H}_{3} ( 1-\beta ) ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7} ) \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{7}V_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{7}}{S_{7}V_{7}I}\,d \boldsymbol{\ell }\\ &\quad {}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{7}I_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{7}I}\,d \boldsymbol{\ell }\\ &\quad {}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{7}V_{7}+ \vartheta _{2}S_{7}I_{7} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }) \frac{L(t-\boldsymbol{\ell })I_{7}}{L_{7}I}\,d\boldsymbol{\ell } \\ &\quad{}+\mathcal{P} ( \vartheta _{1}S_{7}V_{7}+ \vartheta _{2}S_{7}I_{7} ) -\frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}(\boldsymbol{\ell }) \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{7}}{S_{7}Y_{7}E}\,d \boldsymbol{\ell }\\ &\quad {}-\frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}}\frac{YE_{7}}{Y_{7}E}+\mathcal{P}\vartheta _{3}S_{7}Y_{7}+ \frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}} \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{5}}+ \frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\frac{E(t-\boldsymbol{\ell })Y_{7}}{E_{7}Y}\,d \boldsymbol{\ell } \\ &\quad{}+\mathcal{P}\vartheta _{3}S_{7}Y_{7}+ \frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}}Y_{7}- \frac{\mathcal{P}\vartheta _{1}S_{7}V_{7}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\frac{I(t-\boldsymbol{\ell })V_{7}}{I_{7}V}\,d\boldsymbol{\ell } \\ &\quad{}+\mathcal{P}\vartheta _{1}S_{7}V_{7}+ \lambda \mathcal{H}_{3} ( 1- \beta ) \vartheta _{1}S_{7}V_{7} \int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell })\ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{7}I_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{1}S_{7}V_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })}{SV} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+\beta ( \gamma +\lambda ) \vartheta _{2}S_{7}I_{7}\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{SI} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })\ln \biggl( \frac{L(t-\boldsymbol{\ell })}{L} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+ \frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })}{SY} \biggr) \,d\boldsymbol{\ell }\\ &\quad {}+ \biggl( \frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{5}}+ \frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}} \bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\ln \biggl( \frac{E(t-\boldsymbol{\ell })}{E} \biggr) \,d \boldsymbol{\ell } \\ &\quad{}+\frac{\mathcal{P}\vartheta _{1}S_{7}V_{7}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell })\ln \biggl( \frac{I(t-\boldsymbol{\ell })}{I} \biggr) \,d\boldsymbol{\ell }. \end{aligned}$$
Using the equalities given by (10) and (11) in case of \(n=m=7\), we get
$$\begin{aligned} \frac{d\Phi _{7}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{7})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7}+\vartheta _{3}S_{7}Y_{7} ) \biggl[ \frac{S_{7}}{S}-1- \ln \biggl( \frac{S_{7}}{S} \biggr) \biggr] \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{7}V_{7} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{7}}{S_{7}V_{7}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{7}}{S_{7}V_{7}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{7}I_{7} \\ &\quad {}\times\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{7}}{S_{7}I_{7}L}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{7}}{S_{7}I_{7}L} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{7}V_{7} \\ &\quad {}\times\int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{7}}{S_{7}V_{7}I}-1- \ln \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{7}}{S_{7}V_{7}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{7}I_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{7}I}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{7}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7} ) \\ &\quad {}\times\int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell })) \biggl[ \frac{L(t-\boldsymbol{\ell })I_{7}}{L_{7}I}-1-\ln \biggl( \frac{L(t-\boldsymbol{\ell })I_{7}}{L_{7}I} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \biggl[ \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{7}}{S_{7}Y_{7}E}-1-\ln \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{7}}{S_{7}Y_{7}E} \biggr) \biggr] \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}} \biggl[ \frac{YE_{7}}{Y_{7}E}-1-\ln \biggl( \frac{YE_{7}}{Y_{7}E} \biggr) \biggr] \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{5}}+\frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell }) \biggl[ \frac{E(t-\boldsymbol{\ell })Y_{7}}{E_{7}Y}-1-\ln \biggl( \frac{E(t-\boldsymbol{\ell })Y_{7}}{E_{7}Y} \biggr) \biggr] \,d \boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{7}V_{7}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \biggl[ \frac{I(t-\boldsymbol{\ell })V_{7}}{I_{7}V}-1-\ln \biggl( \frac{I(t-\boldsymbol{\ell })V_{7}}{I_{7}V} \biggr) \biggr] \,d \boldsymbol{\ell }. \end{aligned}$$
(28)
Therefore, Eq. (28) becomes
$$\begin{aligned} \frac{d\Phi _{7}}{dt} & =-\varrho \mathcal{P} \frac{(S-S_{7})^{2}}{S}-\mathcal{P} ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7}+\vartheta _{3}S_{7}Y_{7} ) \digamma \biggl( \frac{S_{7}}{S} \biggr) \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{1}S_{7}V_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })L_{7}}{S_{7}V_{7}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\lambda \mathcal{H}_{3} ( 1-\beta ) \vartheta _{2}S_{7}I_{7}\int _{0}^{\kappa _{1}}\bar{\mathcal{H}}_{1}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })L_{7}}{S_{7}I_{7}L} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{1}S_{7}V_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })V(t-\boldsymbol{\ell })I_{7}}{S_{7}V_{7}I} \biggr) \,d \boldsymbol{ \ell } \\ &\quad{}-\beta ( \gamma +\lambda ) \vartheta _{2}S_{7}I_{7} \int _{0}^{\kappa _{2}}\bar{\mathcal{H}}_{2}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })I(t-\boldsymbol{\ell })}{S_{7}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\lambda \mathcal{H}_{1} ( 1-\beta ) ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7} ) \int _{0}^{ \kappa _{3}}\bar{\mathcal{H}}_{3}( \boldsymbol{\ell }))\digamma \biggl( \frac{L(t-\boldsymbol{\ell })I_{7}}{L_{7}I} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{4}} \int _{0}^{\kappa _{4}}\bar{\mathcal{H}}_{4}( \boldsymbol{\ell }) \digamma \biggl( \frac{S(t-\boldsymbol{\ell })Y(t-\boldsymbol{\ell })E_{7}}{S_{7}Y_{7}E} \biggr) \,d \boldsymbol{ \ell }-\frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}} \digamma \biggl( \frac{YE_{7}}{Y_{7}E} \biggr) \\ &\quad{}- \biggl( \frac{\mathcal{P}\vartheta _{3}S_{7}Y_{7}}{\mathcal{H}_{5}}+\frac{\mathcal{P}rY_{7}}{\varphi \mathcal{H}_{4}\mathcal{H}_{5}} \biggr) \int _{0}^{\kappa _{5}}\bar{\mathcal{H}}_{5}( \boldsymbol{\ell })\digamma \biggl( \frac{E(t-\boldsymbol{\ell })Y_{7}}{E_{7}Y} \biggr) \,d\boldsymbol{\ell } \\ &\quad{}-\frac{\mathcal{P}\vartheta _{1}S_{7}V_{7}}{\mathcal{H}_{6}} \int _{0}^{\kappa _{6}}\bar{\mathcal{H}}_{6}( \boldsymbol{\ell }) \digamma \biggl( \frac{I(t-\boldsymbol{\ell })V_{7}}{I_{7}V} \biggr) \,d \boldsymbol{ \ell }. \end{aligned}$$
Hence, \(\frac{d\Phi _{7}}{dt}\leq 0\) for all \(S,L,I,E,Y,V>0\). Similar to the previous theorems, one can show that \(\frac{d\Phi _{7}}{dt}=0\) when \((S,L,I,E,Y,V)=(S_{7},L_{7},I_{7},E_{7},Y_{7},V_{7})\). The solutions of system (5) converge to \(\Upsilon _{7}^{{\prime }}\) which includes elements with \((S,L,I,E,Y,V)(t)=(S_{7},L_{7},I_{7},E_{7},Y_{7},V_{7})\). Then \(\frac{dI(t)}{dt}=\frac{dY(t)}{dt}=0\). The third and fifth equations of system (5) become
$$\begin{aligned} &0 =\frac{dI(t)}{dt}=\beta \mathcal{H}_{2} ( \vartheta _{1}S_{7}V_{7}+\vartheta _{2}S_{7}I_{7} ) +\lambda \mathcal{H}_{3}L_{7}-aI_{7}- \mu _{1}C^{I}(t)I_{7}, \\ &0 =\frac{dY(t)}{dt}=\psi \mathcal{H}_{5}E_{7}-\delta Y_{7}-\mu _{2}C^{Y}(t)Y_{7}, \end{aligned}$$
which yield \(C^{I}(t)=C_{7}^{I}\) and \(C^{Y}(t)=C_{7}^{Y}\) for all t, and hence 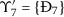 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 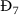 is GAS. □
is GAS. □
 , where \(S_{0}=\eta /\varrho \). In this case, the body is free from HTLV and HIV.
, where \(S_{0}=\eta /\varrho \). In this case, the body is free from HTLV and HIV. , where
, where
 describes the case of persistent HIV monoinfection without immune response.
describes the case of persistent HIV monoinfection without immune response. , where
, where
 describes a persistent HTLV monoinfection without immune response.
describes a persistent HTLV monoinfection without immune response. and can be calculated by different methods such as (a) the next-generation matrix method of van den Driessche and Watmough [
63
], (b) local stability of the infection-free equilibrium
and can be calculated by different methods such as (a) the next-generation matrix method of van den Driessche and Watmough [
63
], (b) local stability of the infection-free equilibrium
 , and (c) the existence of the chronic HIV and HTLV monoinfection equilibria with inactive immune response. In the present paper, we derive
\(\Re _{1}\)
and
\(\Re _{2}\)
by method (c).
, and (c) the existence of the chronic HIV and HTLV monoinfection equilibria with inactive immune response. In the present paper, we derive
\(\Re _{1}\)
and
\(\Re _{2}\)
by method (c).
 , where
, where
 , where
, where
 , where
, where
 , where
, where
 , where
, where
 exists when \(\Re _{7}>1\) and \(\Re _{8}>1\).
exists when \(\Re _{7}>1\) and \(\Re _{8}>1\). is globally asymptotically stable (GAS).
is globally asymptotically stable (GAS).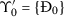 . Applying Lyapunov–LaSalle asymptotic stability (LLAS) theorem [66–68], we get that
. Applying Lyapunov–LaSalle asymptotic stability (LLAS) theorem [66–68], we get that 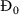 is GAS. □
is GAS. □ is GAS.
is GAS.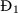 are given by
are given by
 . Therefore, using LLAS theorem we get that
. Therefore, using LLAS theorem we get that  is GAS. □
is GAS. □ is GAS.
is GAS.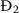
 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get  is GAS. □
is GAS. □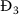 is GAS.
is GAS.
 does not exist since \(E_{5}\leq 0\) and \(Y_{5}\leq 0\). In this case
does not exist since \(E_{5}\leq 0\) and \(Y_{5}\leq 0\). In this case
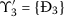 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 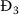 is GAS. □
is GAS. □ is GAS.
is GAS.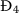
 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 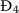 is GAS. □
is GAS. □ is GAS.
is GAS.
 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get  is GAS. □
is GAS. □ is GAS.
is GAS.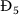
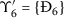 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 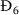 is GAS. □
is GAS. □ is GAS.
is GAS.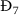
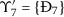 . Applying LLAS theorem, we get
. Applying LLAS theorem, we get 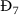 is GAS. □
is GAS. □ ): \(\vartheta _{1}=0.0002\), \(\vartheta _{2}=0.0001\), \(\vartheta _{3}=0.001\), \(\sigma _{1}=0.3\), and \(\sigma _{2}=0.5\). For this set of parameters, we have \(\Re _{1}=0.76<1\) and \(\Re _{2}=0.27<1\). Figure 1 illustrates that the trajectories starting different initials converge to the steady state
): \(\vartheta _{1}=0.0002\), \(\vartheta _{2}=0.0001\), \(\vartheta _{3}=0.001\), \(\sigma _{1}=0.3\), and \(\sigma _{2}=0.5\). For this set of parameters, we have \(\Re _{1}=0.76<1\) and \(\Re _{2}=0.27<1\). Figure 1 illustrates that the trajectories starting different initials converge to the steady state  . This supports the global stability result of Theorem 1. Here, a healthy state will be reached where both viruses are absent.
. This supports the global stability result of Theorem 1. Here, a healthy state will be reached where both viruses are absent.  ): \(\vartheta _{1}=0.0005\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.0007\), \(\sigma _{1}=0.003\), and \(\sigma _{2}=0.2\). With such a choice we get \(\Re _{2}=0.19<1<1.96=\Re _{1}\), \(\Re _{3}=0.34<1\), and hence \(\Re _{2}/\Re _{1}=0.1<1\). The steady state
): \(\vartheta _{1}=0.0005\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.0007\), \(\sigma _{1}=0.003\), and \(\sigma _{2}=0.2\). With such a choice we get \(\Re _{2}=0.19<1<1.96=\Re _{1}\), \(\Re _{3}=0.34<1\), and hence \(\Re _{2}/\Re _{1}=0.1<1\). The steady state  exists with
exists with  . The stability of
. The stability of  given in Theorem 2 is shown in Fig. 2. This leads to the case where HIV monoinfection is chronic but with an ineffective CTL immunity.
given in Theorem 2 is shown in Fig. 2. This leads to the case where HIV monoinfection is chronic but with an ineffective CTL immunity.  ): \(\vartheta _{1}=0.0001\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.005\), \(\sigma _{1}=0.001\), and \(\sigma _{2}=0.05\). Then we calculate \(\Re _{1}=0.72<1<1.34=\Re _{2}\), \(\Re _{4}=0.67<1\), and then \(\Re _{1}/\Re _{2}=0.54<1\) and
): \(\vartheta _{1}=0.0001\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.005\), \(\sigma _{1}=0.001\), and \(\sigma _{2}=0.05\). Then we calculate \(\Re _{1}=0.72<1<1.34=\Re _{2}\), \(\Re _{4}=0.67<1\), and then \(\Re _{1}/\Re _{2}=0.54<1\) and  . We can see from Fig. 3 that the system’s solutions tend to
. We can see from Fig. 3 that the system’s solutions tend to  , which is compatible with Theorem 3. This case means that an HTLV monoinfection is chronic with an ineffective CTL immunity.
, which is compatible with Theorem 3. This case means that an HTLV monoinfection is chronic with an ineffective CTL immunity.  ): \(\vartheta _{1}=0.0005\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.002\), \(\sigma _{1}=0.05\), and \(\sigma _{2}=0.005\). Then we calculate \(\Re _{3}=1.52>1\) and \(\Re _{5}=0.42<1\). Figure 4 shows that the trajectories starting with different states tend to
): \(\vartheta _{1}=0.0005\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.002\), \(\sigma _{1}=0.05\), and \(\sigma _{2}=0.005\). Then we calculate \(\Re _{3}=1.52>1\) and \(\Re _{5}=0.42<1\). Figure 4 shows that the trajectories starting with different states tend to  . Therefore,
. Therefore,  is GAS, and this supports Theorem 4. Hence, an HIV monoinfection is chronic with effective HIV-specific CTL immunity.
is GAS, and this supports Theorem 4. Hence, an HIV monoinfection is chronic with effective HIV-specific CTL immunity.  ): \(\vartheta _{1}=0.0002\), \(\vartheta _{2}=0.0002\), \(\vartheta _{3}=0.02\), \(\sigma _{1}=0.07\), and \(\sigma _{2}=0.4\). Then we calculate \(\Re _{4}=3.57>1\) and \(\Re _{6}=0.60<1\), and
): \(\vartheta _{1}=0.0002\), \(\vartheta _{2}=0.0002\), \(\vartheta _{3}=0.02\), \(\sigma _{1}=0.07\), and \(\sigma _{2}=0.4\). Then we calculate \(\Re _{4}=3.57>1\) and \(\Re _{6}=0.60<1\), and  exists with
exists with  . We observe from Fig. 5 that the system’s trajectories tend to
. We observe from Fig. 5 that the system’s trajectories tend to  and it is GAS. Here, an HTLV monoinfection is chronic with effective HTLV-specific CTL immunity.
and it is GAS. Here, an HTLV monoinfection is chronic with effective HTLV-specific CTL immunity.  ): \(\vartheta _{1}=0.001\), \(\vartheta _{2}=0.0001\), \(\vartheta _{3}=0.005\), \(\sigma _{1}=0.15\), and \(\sigma _{2}=0.01\). Then we calculate \(\Re _{5}=1.15>1\), \(\Re _{8}=0.22<1\), and \(\Re _{1}/\Re _{2}=2.42>1\). The numerical solutions of the system drawn in Fig. 6 confirm that
): \(\vartheta _{1}=0.001\), \(\vartheta _{2}=0.0001\), \(\vartheta _{3}=0.005\), \(\sigma _{1}=0.15\), and \(\sigma _{2}=0.01\). Then we calculate \(\Re _{5}=1.15>1\), \(\Re _{8}=0.22<1\), and \(\Re _{1}/\Re _{2}=2.42>1\). The numerical solutions of the system drawn in Fig. 6 confirm that  exists and is GAS. This case leads to a chronic coinfection with HTLV and HIV where the HIV-specific CTL immunity is effective while the HTLV-specific CTL immunity is ineffective.
exists and is GAS. This case leads to a chronic coinfection with HTLV and HIV where the HIV-specific CTL immunity is effective while the HTLV-specific CTL immunity is ineffective.  ): \(\vartheta _{1}=0.0004\), \(\vartheta _{2}=0.0002\), \(\vartheta _{3}=0.01\), \(\sigma _{1}=0.007\), and \(\sigma _{2}=0.7\). We compute \(\Re _{6}=1.32>1\), \(\Re _{7}=0.55<1\), and \(\Re _{2}/\Re _{1}=1.77>1\). According to these values, we obtain that
): \(\vartheta _{1}=0.0004\), \(\vartheta _{2}=0.0002\), \(\vartheta _{3}=0.01\), \(\sigma _{1}=0.007\), and \(\sigma _{2}=0.7\). We compute \(\Re _{6}=1.32>1\), \(\Re _{7}=0.55<1\), and \(\Re _{2}/\Re _{1}=1.77>1\). According to these values, we obtain that  exists. The numerical solutions of our system plotted in Fig. 7 show that
exists. The numerical solutions of our system plotted in Fig. 7 show that  is GAS (Theorem 7). This case leads to a chronic coinfection with HTLV and HIV where the HTLV-specific CTL immunity is effective and the HIV-specific CTL immunity is not working.
is GAS (Theorem 7). This case leads to a chronic coinfection with HTLV and HIV where the HTLV-specific CTL immunity is effective and the HIV-specific CTL immunity is not working.  ): \(\vartheta _{1}=0.0005\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.01\), \(\sigma _{1}=0.1\), and \(\sigma _{2}=0.3\). These data give \(\Re _{7}=1.33>1\) and \(\Re _{8}=1.81>1\). According to these values, the steady state
): \(\vartheta _{1}=0.0005\), \(\vartheta _{2}=0.0003\), \(\vartheta _{3}=0.01\), \(\sigma _{1}=0.1\), and \(\sigma _{2}=0.3\). These data give \(\Re _{7}=1.33>1\) and \(\Re _{8}=1.81>1\). According to these values, the steady state  exists. Figure 8 illustrates that the solutions of the system initiating with three different states tend to
exists. Figure 8 illustrates that the solutions of the system initiating with three different states tend to  . In this case, a chronic coinfection with HTLV and HIV is reached where both immune responses are well working.
. In this case, a chronic coinfection with HTLV and HIV is reached where both immune responses are well working.  can be changed. Let us calculate the critical value of the time delay that changes the stability of
can be changed. Let us calculate the critical value of the time delay that changes the stability of  . Without loss of generality, we let the parameters \(\boldsymbol{\ell }=\boldsymbol{\ell }_{1}=\boldsymbol{\ell }_{2}=\boldsymbol{\ell }_{3}\) and fix \(\boldsymbol{\ell }_{j}\), \(j=5,6\), and write \(\Re _{1}\) and \(\Re _{2}\) as functions of ℓ and \(\boldsymbol{\ell }_{4}\), respectively, as follows:
. Without loss of generality, we let the parameters \(\boldsymbol{\ell }=\boldsymbol{\ell }_{1}=\boldsymbol{\ell }_{2}=\boldsymbol{\ell }_{3}\) and fix \(\boldsymbol{\ell }_{j}\), \(j=5,6\), and write \(\Re _{1}\) and \(\Re _{2}\) as functions of ℓ and \(\boldsymbol{\ell }_{4}\), respectively, as follows:
 is GAS. Let us choose the value \(\boldsymbol{\ell }_{5}=0.2\) and \(\boldsymbol{\ell }_{6}=0.1\) and compute \(\boldsymbol{\ell }^{\min }\), \(\boldsymbol{\ell }_{4}^{\min }\) as \(\boldsymbol{\ell }^{\min }=2.73728\), \(\boldsymbol{\ell }_{4}^{\min }=2.36794\). It follows that:
is GAS. Let us choose the value \(\boldsymbol{\ell }_{5}=0.2\) and \(\boldsymbol{\ell }_{6}=0.1\) and compute \(\boldsymbol{\ell }^{\min }\), \(\boldsymbol{\ell }_{4}^{\min }\) as \(\boldsymbol{\ell }^{\min }=2.73728\), \(\boldsymbol{\ell }_{4}^{\min }=2.36794\). It follows that:  is GAS.
is GAS. will lose its stability.
will lose its stability.







