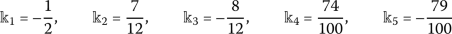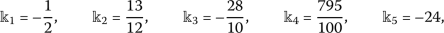- Research
- Open access
- Published:
Entire solutions of a class of algebraic Briot–Bouquet differential equations utilizing majority concept
Advances in Difference Equations volume 2020, Article number: 678 (2020)
Abstract
In this effort, the analytic solution of a class of algebraic Briot–Bouquet differential equations (ABBDE) in the open unit disk is investigated by making use of a major theory. The class is presented by the formula
The conformal analysis (angle-preserving) of the ABBDEs is considered. Analytic outcomes of the ABBDEs are indicated by employing the major method. Some special cases are investigated.
1 Introduction
The algebraic Briot–Bouquet differential equation (ABBDE) is a significant nonlinear differential equation which occurs in many applications such as neuroscience, geometry, economy, banking studies, and physics. The most important property of ABBDE is that it shows that every meromorphic solution of ABBDE belongs to the class of meromorphic functions containing elliptic functions and their degenerates, i.e., the rational functions of one exponential \(e^{\zeta z}\), \(\zeta \in \mathbb{C}\), \(z \in \mathbb{U}=\{z \in \mathbb{C}: |z|<1\}\) and rational functions. Many consequences for higher-order ABBDE are also presented in a sequence of documents (see [1–12]).
The majorization inequality theory (real and complex) has many applications in our real life [13]. For example, they have measured the economy, specifically in the income-distribution (economic inequality), that is, the distribution of income between the primary factors of production. New economists have, furthermore, addressed issues of income distribution, but have absorbed further on the distribution of income persons and households. Important theoretical and policy concerns consist of the balance between income majorization inequality and economic growth, and their often-inverse association. Moreover, the Gini coefficient measures the inequality among the values of a frequency distribution (for example, levels of income) [14]. A Gini coefficient of zero states perfect equality, where all values are the same (for example, where everyone has the same income) [15]. Therefore, the solution of any class of differential equations majoring by a convex function or by special function is very attractive, especially in wealth and health distribution [16].
In this paper, we investigate a class of ABBDEs in the open unit disk. We study the geometric representation for this class and majorize them by employing special function in \(\mathbb{U}\) including the exponential function.
2 Complex ABBDEs
A special class of ABBDEs is studied in [7] taking the structure
where \(\alpha _{\imath }\in \mathbb{C}\), \(\imath =1,2,3\), and
where \(a_{\jmath }, \jmath =0,1,\ldots,k\), are constants (real or complex).
Now, we reorganize (2.1) and consider the geometric possessions by designing some classes of normalized analytic functions in \(\mathbb{U}\). Then the resolution is majorized by engaging special functions in \(\mathbb{U}\). Equation (2.1) suggests the homogeneous form when \(\alpha _{1} \neq 0\),
To study Eq. (2.2) geometrically, we request the following theory.
Definition 2.1
An analytic function h is subordinated to an analytic function g, written \(h \prec g\), if substitutes for an analytic function w with \(|w(z)| \leq |z| \) such that \(h= (g(w))\) (see [17]). The Ma-Minda classes \(S^{*}(\rho ) \) and \(K(\rho ) \) of starlike and convex functions respectively indicated by \((\frac{z h' (z)}{h(z)} ) \prec \rho (z)\) and \((1+\frac{z h'' (z)}{h'(z)} ) \prec \rho (z)\), where ρ has a positive real part in \(\mathbb{U}\), \(\rho (0)=1\), \(\rho '(0)>1\) and maps \(\mathbb{U}\) onto a starlike-domain.
We recognize our study by applying the above inequality to formulate the following special class.
Definition 2.2
A function of normalized expansion \(\varphi (z)=z+\sum_{n=2}^{\infty }\varphi _{n}z^{n}\), \(z \in \mathbb{U}\) is said to be in the class \(\textbf{M}(\rho )\) if and only if
It is clear that \(P(0)=1\). For example, let \(\varphi (z)=z/(1-z)\), \(z \in \mathbb{U}\), then
Also, for \(\varphi (z)=z/(1-z)^{2} \), \(z \in \mathbb{U}\), we have
In the sequel, we theorize a starlike function with positive real part such as \(e^{z}\) (this function yields an oscillation solution of Eq. (2.1) [7]) and a convex function (univalent)
as well as
is convex univalent in \(\mathbb{U}\) (see [17], p. 415). Note that the coefficients are converging to the Bernoulli numbers. Moreover, the real part of the function \(\varrho _{e}(z)=(e^{z}-1)/z\) satisfies the inequality
Hence, \(\Re ( \frac{e^{\eta z}-1}{\eta z} ) \geq 1/\rho _{e}(-1)= \frac{1}{2} \).
Our calculation is established by the analytic method of Caratheodory functions which are characterized in [18]. Consequently, by making use of major theory, we approximate \(\aleph ^{k}_{\varphi }(z)\) by a special type of \(\rho (z)\), \(z \in \mathbb{U}\) denoted by \(\aleph ^{k}_{\varphi }(z)\ll \rho (z)\). Note that the two functions are under majorization if and only if \(|a_{\jmath }| \leq | \rho _{\jmath }|\) for all \(\jmath =1,2,\ldots \) , where \(a_{\jmath }\) and \(\rho _{\jmath }\) are the coefficients of \(\aleph ^{k}_{\varphi }(z)\) and \(\rho (z)\) respectively. In this situation, we demonstrate adequate conditions of the coefficient constraints of \(\aleph ^{k}_{\varphi }(z)\), for altered values of \(k=0,1,\ldots\) , using a Caratheodory theory.
3 Computations
In this position, we demonstrate our theoretical results.
Theorem 3.1
Let the function \(\varphi \in \textbf{M}(\rho )\) achieve the inequality
where ⋎ is a constant and \(P(z)= ( \frac{z \varphi ' (z)}{\varphi (z)} )^{2}+ b_{2}z ( \frac{z \varphi ' (z)}{\varphi (z)} )+ b_{3}z^{2}\). Then
When \(\curlyvee \geq \max \curlyvee _{k}\),
-
$$ \min \curlyvee _{0}= \frac{ -((e - 1) (-2 + \sqrt{2} + \log (2) - \log (1 + \sqrt{2})))}{(e - 2)} \approx 1.8516\ldots $$
and
$$ \max \curlyvee _{0}= (e - 1) \bigl(\sqrt{2} + \log (2) + \log ( \sqrt{2} - 1)\bigr)\approx 2.106\ldots $$ -
$$ \min \curlyvee _{1}= \frac{ (2 - \sqrt{2} - \log (2) + \log (1 + \sqrt{2}))}{\log (e - 1)} \approx 1.5\ldots $$
and
$$ \max \curlyvee _{1}= \frac{ (-\sqrt{(}2) - \log (2) - \log (\sqrt{(}2) - 1))}{(\log (e - 1) - 1)} \approx 2.839\ldots $$ -
$$ \min \curlyvee _{2}= \frac{2 - \sqrt{2} + \log (1/2 + 1/\sqrt{2})}{(e - 2) } \approx 1.077\ldots $$
and
$$ \max \curlyvee _{2}= e \bigl(\sqrt{2} + \log (2) - \log (1 + \sqrt{2})\bigr) \approx 3.33\ldots . $$
Proof
Case I: \(k=0\Rightarrow 1+\curlyvee ( z P' (z) ) \prec z+ \sqrt{z^{2}+1}\).
Set a function \(\Gamma _{\curlyvee }: \mathbb{U} \rightarrow \mathbb{C}\) admitting the structure
Clearly, \(\Gamma _{\curlyvee }(z)\) is analytic in \(\mathbb{U}\) such that \(\Gamma _{\curlyvee }(0)=1\) and it is the outcome of the differential equation
Consequently, we have \(\mathfrak{Q}(z):= \curlyvee ( z \Gamma _{\curlyvee }' (z) )= z+\sqrt{z^{2}+1}-1 \) is starlike in \(\mathbb{U}\). Then for \(\mathfrak{J}(z):=\mathfrak{Q}(z)+1\), we conclude that
Thus, the Miller–Mocanu lemma (see [17], p. 132) yields that
To finish this event, we only need to prove that \(\Gamma _{\curlyvee }(z) \prec \rho _{e}(z)\). Clearly, the function \(\Gamma _{\curlyvee }(z)\) is increasing in the interval \((-1,1)\) that has the inequality
Because the function \(\rho _{e}(z)\) achieves the inequality for real ϑ
then the consequence inequality holds
if ⋎ fulfills the upper and lower bounds
and
This yields the subordination inequalities
Case II: \(k=1 \Rightarrow 1+\curlyvee (\frac{ z P' (z)}{P(z)} ) \prec z+\sqrt{z^{2}+1}\).
Now we present a function \(\Pi _{\curlyvee }: \mathbb{U} \rightarrow \mathbb{C}\) structuring by the formula
Obviously, \(\Pi _{\curlyvee }(z)\) is analytic in \(\mathbb{U}\) having \(\Pi _{\curlyvee }(0)=1\) and it is an outcome of the differential equation
By using \(\mathfrak{Q}(z) = z+\sqrt{z^{2}+1}-1 \), which is starlike in \(\mathbb{U}\) and \(\mathfrak{J}(z)=\mathfrak{Q}(z)+1\), we get
Then again, by Miller–Mocanu lemma, we obtain
Consequently, the following inequality holds:
if ⋎ has the upper and lower bounds
and
This indicates the subordination inequalities
Case III: \(k=2 \Rightarrow 1+\curlyvee (\frac{ z P' (z)}{P^{2}(z)} ) \prec z+\sqrt{z^{2}+1}\).
Now, we introduce a function \(\Pi _{\curlyvee }: \mathbb{U} \rightarrow \mathbb{C}\) having the formal
Clearly, \(\Pi _{\curlyvee }(z)\) is analytic in \(\mathbb{U}\) admitting \(\Pi _{\curlyvee }(0)=1\), and it is the outcome of the differential equation
By utilizing \(\mathfrak{Q}(z) = z+\sqrt{z^{2}+1}-1 \), which is starlike in \(\mathbb{U}\) and \(\mathfrak{J}(z)=\mathfrak{Q}(z)+1\), we get
Consequently, by Miller–Mocanu lemma, we get
Accordingly, we attain
if ⋎2 admits the upper and lower bounds
and
This yields the subordination inequalities
□
The next result studies the subordination with respect to the function
Theorem 3.2
Let the assumptions of Theorem 3.1hold for a constant ⋏ where
Then
When \(\curlywedge \geq \max \curlywedge _{k}\),
-
$$ \min \curlywedge _{0}= \frac{ (\sqrt{2} + \log (2) + \log (\sqrt{2} - 1))}{(e - 2) } \approx 1.706\ldots $$
and
$$ \max \curlywedge _{0}= -e \bigl(-2 + \sqrt{2} + \log (2) - \log \bigl(1 + \sqrt{(}2)\bigr)\bigr)\approx 2.10399\ldots . $$ -
$$ \min \curlywedge _{1}= \frac{ (-2 + \sqrt{2} + \log (2) + \log (\sqrt{2} - 1))}{(\log (e - 1) - 1)} \approx 1.70\ldots $$
and
$$ \max \curlywedge _{1}= \bigl(\sqrt{2} + \log (2) + \log (\sqrt{2} - 1)\bigr)/ \log (e - 1) \approx 2.2\ldots . $$ -
$$ \min \curlywedge _{2}= -(e - 1) \bigl(-2 + \sqrt{2} + \log (2) - \log (1 + \sqrt{2})\bigr) \approx 1.329\ldots $$
and
$$ \max \curlywedge _{2}= \frac{ ((e - 1) (\sqrt{2} + \log (2) - \log (1 + \sqrt{2})))}{(e - 2) } \approx 2.932\ldots . $$
Proof
State the convex univalent function \(\varrho _{e}(z)= \frac{e^{z}-1}{z}\). It is clear that \(\varrho (0)=1\) with a positive real part. Moreover, it satisfies the inequality
By the conversation of Theorem 3.1, we indicate the following inequality:
if ⋏ has the upper and lower bounds
and
This establishes the subordination inequalities
Similarly, we have
and
This yields the subordination inequalities
Lastly, we get the upper and lower bounds
and
This admits the subordination inequalities
□
4 Majorization
We progress to involve the formula
for some k to investigate the geometric solutions of Eq. (2.1). Dividing Eq. (2.1) by \(\alpha _{1} \neq 0\), we receive
We have the following result.
Theorem 4.1
Consider CADE (4.1) with \(\alpha _{1}=-1\) and \(a_{0}=1\). If \(\varphi \in \textbf{M}(\rho )\) is a convex univalent function in \(\mathbb{U}\) fulfilling the restriction of Theorem 3.1, then the communication values \(a_{\imath }\) have the following construction:
Proof
From Eq. (4.1) together with Theorem 3.1, we have \(\aleph ^{k}_{\varphi }(z) \prec \rho _{e}(z)\). Since φ is convex univalent in ∪, then it indicates the extreme function construction
Thus, we obtain
Moreover, we attain that
where \(B_{n}\) is the Bernoulli numbers having the inequality
Comparing the coefficients of \(\aleph ^{k}_{\varphi }(z) \) and \(\rho _{e}(z)\), we have
□
The next result indicates the value of constant coefficients of \(\aleph ^{k}_{\varphi }\) when φ is starlike in \(\mathbb{U}\).
Theorem 4.2
Consider CADE (4.1) with \(\alpha _{1}=-1\) and \(a_{0}=1\). If \(\varphi \in \textbf{M}(\rho )\) is a starlike function in \(\mathbb{U}\) fulfilling the construction of Theorem 3.1, then the communication values \(a_{\imath }\) have the construction
Proof
Plainly, from the conditions, we get \(\aleph ^{k}_{\varphi }(z) \prec \rho _{e}(z)\). Since φ is starlike in ∪, then it has the extreme function formula
Thus, we get
Contrasting the connections of \(\aleph ^{m}_{\varphi }(z) \) and \(\rho _{e}(z)\), we have
□
Remark 4.3
-
Note that Theorems 4.1 and 4.2 indicate that \(\aleph ^{k}_{\varphi }(z)\) accumulates at \(k=5\), which yields the expansion formulas
$$ \aleph ^{5}_{z/(1-z)}= 1- \frac{z}{2} + \frac{z^{2}}{12} - \frac{z^{4}}{100} + O\bigl(z^{6}\bigr) $$and
$$ \aleph ^{5}_{z/(1-z)^{2}}= 1- \frac{z}{2} + \frac{8 z^{2}}{100} - \frac{2 z^{4}}{100} + O\bigl(z^{6}\bigr). $$ -
One can extend Theorems 4.1 and 4.2 in expressions of α for all estimates. In this suggestion, we get the constant connections
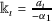 provided \(\alpha \neq 0\)
provided \(\alpha \neq 0\) 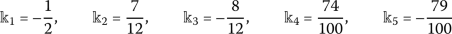
and
respectively.
Availability of data and materials
Not applicable.
Abbreviations
- ABBDE:
-
Algebraic Briot–Bouquet differential equations
References
Ibrahim, R.W., Jahangiri, J.M., Cloud Computing Center: Conformable differential operator generalizes the Briot–Bouquet differential equation in a complex domain. AIMS Math. 4(6), 1582–1595 (2019)
Ibrahim, R.W., Darus, M.: On a class of analytic functions associated to a complex domain concerning q-differential-difference operator. Adv. Differ. Equ. 2019(1), 515 (2019)
Dreyfus, T., Lastra, A., Malek, S.: On the multiple-scale analysis for some linear partial q-difference and differential equations with holomorphic coefficients. Adv. Differ. Equ. 2019(1), 326 (2019)
Ibrahim, R.W., Hadid, S.B., Momani, S.: Generalized Briot–Bouquet differential equation by a quantum difference operator in a complex domain. Int. J. Dyn. Control 8, 762–771 (2020)
Ibrahim, R.W., Elobaid, R.M., Obaiys, S.J.: Symmetric conformable fractional derivative of complex variables. Mathematics 8(3), 363 (2020)
Ibrahim, R.W., Elobaid, R.M., Obaiys, S.J.: Generalized Briot–Bouquet differential equation based on new differential operator with complex connections. Axioms 9(2), 42 (2020)
Shi, X., Liao, L., Zhang, S.: Explicit meromorphic solutions of a certain Briot–Bouquet differential equations. Chin. Ann. Math., Ser. B 41, 383–396 (2020)
Okada, Y., Schafke, R., Tahara, H.: A formal solvability of a coupling equation for PDEs of Briot–Bouquet type (microlocal analysis and asymptotic analysis). RIMS Kokyuroku 2101, 91–97 (2019)
Liao, L., Lu, X.: On solutions of a certain type of Briot–Bouquet equations. Complex Var. Elliptic Equ. 64(8), 1419–1436 (2019)
Saleeby, E.G.: On meromorphic solutions of first-order Briot–Bouquet type PDEs. J. Math. Anal. Appl. 482(1), 123517 (2020)
Acu, M., Oros, G.: Starlikeness condition for a new differential-integral operator. Mathematics 8(5), 694 (2020)
Antonino, J.A., Miller, S.S.: F-classes of univalent functions and F-differential subordinations. Comput. Methods Funct. Theory, 1–19 (2020)
Marshall, A.W., Olkin, I., Arnold, B.C.: Inequalities: Theory of Majorization and Its Applications, vol. 143. Academic Press, New York (1979)
Ibrahim, R.W.: A new approach of utility function based on fractional Gini aggregation operator for intelligent access web selection. SN Appl. Sci. 1(9), 1126 (2019)
Luptacik, M., Nezinsky, E.: Measuring income inequalities beyond the Gini coefficient. Cent. Eur. J. Oper. Res. 28, 561–578 (2020)
Wang, H.-Y., et al.: Comparison of Ferguson’s δ and the Gini coefficient used for measuring the inequality of data related to health quality of life outcomes. Health Qual. Life Outcomes 18, 1–9 (2020)
Miller, S.S., Mocanu, P.T.: Differential Subordinations: Theory and Applications. CRC Press, Boca Raton (2000)
Gandhi, S., Kumar, S., Ravichandran, V.: First order differential subordinations for Caratheodory functions. Kyungpook Math. J. 58(2), 257–270 (2018)
Acknowledgements
The authors would like to thank the editorial office for their advice. Also, the authors wish to express their profound gratitude to the anonymous referees for their careful reading of the manuscript and the very useful comments that have been implemented in the final version of the manuscript.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ibrahim, R.W., Baleanu, D. Entire solutions of a class of algebraic Briot–Bouquet differential equations utilizing majority concept. Adv Differ Equ 2020, 678 (2020). https://doi.org/10.1186/s13662-020-03138-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03138-2
 provided
provided