- Research
- Open access
- Published:
Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series
Advances in Difference Equations volume 2020, Article number: 494 (2020)
Abstract
In the present work, a numerical technique for solving a general form of nonlinear fractional order integro-differential equations (GNFIDEs) with linear functional arguments using Chebyshev series is presented. The recommended equation with its linear functional argument produces a general form of delay, proportional delay, and advanced non-linear arbitrary order Fredholm–Volterra integro-differential equations. Spectral collocation method is extended to study this problem as a matrix discretization scheme, where the fractional derivatives are characterized in the Caputo sense. The collocation method transforms the given equation and conditions to an algebraic nonlinear system of equations with unknown Chebyshev coefficients. Additionally, we present a general form of the operational matrix for derivatives. The introduced operational matrix of derivatives includes arbitrary order derivatives and the operational matrix of ordinary derivative as a special case. To the best of authors’ knowledge, there is no other work discussing this point. Numerical test examples are given, and the achieved results show that the recommended method is very effective and convenient.
1 Introduction
Nonlinear differential (DEs) and integro-differential equations (IDEs) have a great importance in modeling of many phenomena in physics and engineering [1–17]. Fractional differential equations involving the Caputo and other fractional derivatives, which are a generalization of classical differential equations, have attracted widespread attention [18–25]. In the last decade or so, several studies have been carried out to develop numerical schemes to deal with fractional integro-differential equations (FIDEs) of both linear and nonlinear type. The successive approximation methods such as Adomian decomposition [26], He’s variational iteration technique [8], HPM [5], He’s HPM [27], modified HPM [28], finite difference method [29], a modified reproducing kernel discretization method [30], and differential transformation method [31] were used to deal with FIDEs. Spectral methods with different basis were also applied to FIDEs, Chebyshev and Taylor collocation, Haar wavelet, Tau and Walsh series schemes, etc. [32–39] as an example. The collocation method is one of the powerful spectral methods which are widely used for solving fractional differential and integro-differential equations [40–44]. Further, the numerical solution of delay and advanced DEs of arbitrary order has been reported by many researchers [45–58]. Differential equations of advanced argument had fewer contributions in mathematics research compared to delay differential equations, which had a great development in the last decade [59, 60]. Monotone iterative technique was introduced with Riemann–Liouville fractional derivative to deal with FIDEs with advanced arguments [61], while the collocation method with Bessel polynomials treated linear Fredholm integro-differential-difference equations [62]. In our previous work, Tau method with the Chebyshev polynomials was employed to deal with linear fractional differential equations with linear functional arguments [63]; therefore, the Chebyshev collocation method was extended to fractional differential equations with delay [64]. The equations with functional form of argument represent mixed type equations delay, proportional delay, and advanced differential equations. All reported works considered a generalization of equations with functional argument with integer order derivative or with fractional derivative in the linear case.
In this work, we introduce a general form of nonlinear fractional integro-differential equations (GNFIDEs) with linear functional arguments, which is a more general form of nonlinear fractional pantograph and Fredholm–Volterra integro-differential equations with linear functional arguments [65–69]. The spectral collocation method is used with Chebyshev polynomials of the first kind as a matrix discretization method to treat the proposed equations. An operational matrix for derivatives is presented. The introduced operational matrix of derivatives includes fractional order derivatives and the operational matrix of ordinary derivative as a special case. No other studies have discussed this point.
The proposed GNFIDEs with linear functional arguments are presented as follows:
where \(x\in [a,b]\), \(Q_{k,i}(x), P_{h,j}(x)\), \(f(x)\), \(V_{c}(x,t), K_{d}(x,t)\) are well-defined functions, and \(a,b,p_{i},\xi _{i},q_{j}, \zeta _{j}\in \Re \) where \(p_{i},q_{j}\neq 0\), \(\nu _{i} \geq 0\), \(\alpha _{j} \geq 0\), \(\upsilon _{d}\geq 0\), \(\beta _{c}\geq 0\) and \(i - 1 < \nu _{i} \leq i \), \(j - 1 < \alpha _{j} \leq j \), \(d - 1 < \upsilon _{d}\leq d\), \(c - 1 < \beta _{c}\leq c\), \(n_{i} \in \mathbb{N}\), under the conditions
where \(\eta _{i}\in [a,b]\), and m is the greatest integer order derivative, or the highest integer order greater than the fractional derivative. The general form (1) contains at least three different arguments, then the following corollary defines the interval that the independent variable x belongs to. Chebyshev polynomials of the first kind are used in this work to approximate the solution of suggested equation (1). The Chebyshev polynomials are characterized on \([-1, 1]\).
Corollary 1.1
The independent variable x of (1) belongs to \([a,b]\), which is the intersection of the intervals of the different arguments and \([-1,1]\)i.e. \(x\in [a,b]=[\frac{-1+\xi _{i}}{p_{i}},\frac{1+\xi _{i}}{p_{i}}] \cap [\frac{-1+\zeta _{j}}{q_{j}},\frac{1+\zeta _{j}}{q_{j}}] \cap [-1,1]\).
2 General notations
In this section, some definitions and properties for the fractional derivative and Chebyshev polynomials are listed [63, 64, 70, 71].
2.1 The Caputo fractional derivative
The Caputo fractional derivative operator \(D^{\gamma }_{t}\) of order γ is characterized in the following form:
where \(x > 0\), \(n-1 < \gamma \leq n, n \in \mathbb{N}_{0}\), and \(\mathbb{N}_{0} = \mathbb{N}-\{0\}\).
-
\(D^{\gamma }_{t} \sum_{i=0}^{m}\lambda _{i} \varPsi _{i}(x)= \sum_{i=0}^{m} \lambda _{i} D^{\gamma }_{t}\varPsi _{i}(x)\), where \(\lambda _{i}\) and γ are constants.
-
The Caputo fractional differentiation of a constant is zero.
-
\(D^{\gamma }_{t} x^{k}= \bigl\{ \scriptsize{ \begin{array}{l@{\quad}l} 0 & \text{for } k\in \mathbb{N}_{0}\text{ and } k<\lceil \gamma \rceil, \\ \frac{\varGamma (k+1) x^{k-\gamma }}{\varGamma (k+1-\gamma )} & \text{for } k\in \mathbb{N}_{0} \text{ and } k\geq \lceil \gamma \rceil, \end{array}}\)
where \(\lceil \gamma \rceil \) denotes to the smallest integer greater than or equal to γ.
2.2 Chebyshev polynomials
The Chebyshev polynomials \(T_{n}(x)\) of the first kind are defined as follows: orthogonal polynomials in x of degree n are defined on \([-1, 1]\) such that
where \(x=\cos \theta \) and \(\theta \in [0, \pi ]\). The polynomials \(T_{n}(x)\) are generated by using the following recurrence relations:
with initials
Corollary 2.1
The Chebyshev polynomials \(T_{n} (x)\)are explicitly expressed in terms of \(x^{n} \)in the following form:
where
3 Procedure solution using the collocation method
The solution \(y(x)\) of (1) may be expanded by Chebyshev polynomial series of the first kind as follows [64]:
By truncating series (5) to \(N<\infty \), the approximate solution is expressed in the following form:
where \(T(x) \) and C are matrices given by
Now, using (4), relation (6) may written in the following form:
where W is a square lower triangle matrix with size \((N+1)\times (N+1) \) given by
where
For example,
Then, by substituting from (6) in (1), we get
We can write (9) as follows:
The collocation points are defined in the following form:
where
By substituting the collocation points (11) in (10), we get
In the following theorem we introduce a general form of operational matrix of the row vector \(T(x)\) in the representation as (7), such that the process includes the fractional order derivatives, and ordinary operational matrix given as a special case when \(\alpha _{i}\rightarrow \lceil \alpha _{i}\rceil \).
Theorem 1
Assume that the Chebyshev row vector \(T(x)\)is represented as (7), then the fractional order derivative of the vector \(D^{\alpha _{i}}T(x)\)is
where
where \(B_{\alpha _{i}}\)is an \((N+1)\times (N+1)\)square upper diagonal matrix, the elements \(b_{r,s}\)of \(B_{\alpha _{i}}\)can be written as follows:
where \(i-1 < \alpha _{i}\leqslant i, N\geqslant \lceil \alpha _{i} \rceil \).
Proof
Since
if \(0 < \alpha _{1}\leqslant 1\), using Caputo’s fractional properties, we get
As \(\alpha _{1} \longrightarrow 1\), the system reduces to the ordinary case \((B_{\alpha _{1}}\longrightarrow B)\) (see [64]).
Also \(1 < \alpha _{2}\leqslant 2\), then
As \(\alpha _{2}\longrightarrow 2\), the system reduces to the ordinary case \((B_{\alpha _{2}}\longrightarrow B^{2})\) (see [64]).
By the same way, if we take \(2 < \alpha _{3}\leqslant 3\), then
As \(\alpha _{3}\longrightarrow 3\), the system reduces to the ordinary case \((B_{\alpha _{3}}\longrightarrow B^{3})\) (see [64]).
By induction, \(i-1 < \alpha _{i}\leqslant i\), then
and \(B_{\alpha _{i}}\) as in (15), where the proposed operational matrix represents a kind of unification of ordinary and fractional case. □
Now, we give the matrix representation for all terms in (12) as representation (13).
∗ The first term in (12) can be written as follows:
where
In addition, \(H_{p_{i}}\) is a square diagonal matrix of the coefficients for the linear argument, and the elements of \(H_{p_{i}}\) can be written as follows:
Moreover, \(E_{\xi _{i}}\) is a square upper triangle matrix for the shift of the linear argument, and the form of \(E_{\xi _{i}}\) is
∗ The second term in (12) can be written as follows:
where
and \(B_{h}\) is the same as \(B_{\alpha _{i}} \) when \(h=\lceil \alpha _{i}\rceil \).
The matrix representation for the variable coefficients takes the form
∗ Matrix representation for integral terms: Now, we try to find the matrix form corresponding to the integral term. Assume that \(K_{d} (x,t)\) can be expanded to univariate Chebyshev series with respect to t as follows:
Then the matrix representation of the kernel function \(K_{d} (x,t) \) is given by
where
Substituting relations (13) and (27) in the present integral part, we obtain
where
or
So, the present integral term can be written as:
where
∗ Matrix representation for integral terms: Now, we try to find the matrix form corresponding to the integral term. By the same way \(V_{c} (x,t)\) can be expanded as (26)
Then the matrix representation of the kernel function \(V_{c} (x,t) \) is given by
where
Substituting relations (13) and (31) in the present integral part, we obtain
where
or
So, the present integral term can be written as follows:
where
Now, by substituting equations (24), (25), and (29) into (12), we have the fundamental matrix equation
We can write (34) in the form
where
Corollary 3.1
Suppose \(k\geqslant 2\), then the matrix representation for the terms free of derivatives in (1), by using (6), we obtain
We can achieve the matrix form of (37) by using the collocation points as follows:
∗ We can achieve the matrix form for conditions (2) by using (6) on the form
or
where
Consequently, replacing m rows of the augmented matrix \([O;F]\) by rows of the matrix \([M_{i};\mu _{i}]\), we have \([\bar{O};\bar{F}]\) or
System (34), together with conditions, gives \((N+1)\) nonlinear algebraic equations which can be solved for the unknown \(c_{n}\), \(n = 0, 1, 2, \ldots,N\). Consequently, \(y(x)\) given as equation (6) can be calculated.
4 Numerical examples
In this section, several numerical examples are given to illustrate the accuracy and the effectiveness of the method.
4.1 Error estimation
if the exact solution of the proposed problem is known, then the absolute error will be estimated from the following:
where \(y_{\mathrm{Exact}}(x)\) is the exact solution and \(y_{\mathrm{Approximate}}(x)\) is the achieved solution at some N. The calculation of \(L_{2} \) error norm also can obtained as follows:
where h is the step size along the given interval. We can easily check the accuracy of the suggested method by the residual error. When the solution \(y_{\mathrm{Approximate}}(x)\) and its derivatives are substituted in (1), the resulting equation must be satisfied approximately, that is, for \(x\in [a,b]\), \(l=0,1,2,\ldots \)
where \(E_{N}\leq 10^{-\pounds}\) (£ positive integer) and \(y(x)\) considered as \(y_{\mathrm{Approximate}}(x)\).
Example 1
Consider the following NFIDE with linear functional argument:
The ICs are \(y(1)=2\), \(y^{\prime }(1)=2\), and \(y^{\prime \prime }(1)=2\) and the exact solution is \(y(x)=x^{2}+x\) at \(\nu _{2}=1.5\), \(\alpha _{3}=2.5\), \(\upsilon _{2}=1.5\), \(\beta _{2}=1.8 \), where \(f(x)=- 0.990113 e^{x} + 0.300901 x^{2.5} + 2.25676 x^{0.5} (x + x^{2})^{2} + (x + x^{2})^{4} + (x + x^{2})^{4} (2 + 4 (1 + 2 x))\). We apply the suggested method with \(N = 4\), and by the fundamental matrix equation of the problem defined by (34), we have
where
Equation (45) and conditions present a nonlinear system of \((N + 1)\) algebraic equations in the coefficients \(c_{i}\). The solution of this system at \(N=4\) gives the Chebyshev coefficients as follows:
Therefore, the approximate solution of this example using (6) is given by
which is the exact solution of problem (44).
Example 2
Consider the following nonlinear fractional integro-differential equation:
The ICs are \(y(0)=1\), \(y^{\prime }(0)=1\), and the exact solution is \(y(x)=x^{3}+1\) at \(\alpha _{2}=1.8\), \(\nu _{2}=2\), where \(f(x)=\frac{9}{10} + \frac{3 e^{x}}{4}- \frac{3 x}{4} - \frac{x^{2}}{2}+ 32.6737 x^{2.2} -\frac{11 x^{5}}{10} + 6 (-1 + x) (1 + x^{3})^{3}\).
The matrix representation of equation (47) is
Equation (48) and conditions present a nonlinear system of \((N + 1)\) algebraic equations in the coefficients \(c_{i}\), the solution of this system at \(N=4\) gives the Chebyshev coefficients
Thus, the solution of this problem becomes
which is the exact solution of problem (47).
Example 3
Consider the following nonlinear fractional integro-differential equation with advanced argument:
The subjected conditions are \(y(1)=3\), \(y^{\prime }(1)=3\), and the exact solution is \(y(x)=x^{2}+x+1\) at \(\alpha _{2}=1.6\), where \(f(x)=-8.42841 - 3.20484 e^{x} + (22 x)/3 - 1.35406 (1 + 3 x)^{2.5} - 1.28958 (1 + 3 x)^{3.5} + 2 (1 + x + x^{2})^{2} + 2.25412 x^{0.4} (1 + x + x^{2})^{3} + x (1 + 2 (1 + x)) - x ( 1.50451 (1 + 3 x)^{1.5} + 1.2036 (1+ 3 x)^{2.5})\). The fundamental matrix equation of the problem becomes as follows:
Equation (50) and conditions present a nonlinear system of \((N + 1)\) algebraic equations in the coefficients \(c_{i}\). The solution of this system at \(N=4\) gives the Chebyshev coefficients in the following form:
Thus, the solution of the proposed problem becomes
which is the exact solution of problem (50).
Example 4
Consider the following linear fractional integro-differential equation with argument [65]:
The ICs are \(y(0)=4\), \(y^{\prime }(0)=-4\), and the exact solution is \(y(x)=x^{2}-4x+4\) at \(\nu _{2}=2\), where \(f(x)=\frac{53}{3} - 14 x + 2 x^{2}\). We apply the suggested method with \(N = 4\), then the fundamental matrix equation of the problem becomes as follows:
Equation (53) and conditions present a linear system of \((N + 1)\) algebraic equations in the coefficients \(c_{i}\). The solution of this system at \(N=4\) gives the Chebyshev coefficients as follows:
Thus, the solution of this problem becomes
In Table 1 the comparison of the absolute errors for the present scheme at \(N=4\), where \(\nu _{2}=2\), and the method of reference [65] at \(N=8, 10\) is presented. Also, Table 2 shows the numerical values of the approximate solution for various N with reference [65] and the exact solution. The residual error according to (43) is given in Tables 3 and 4 as follows: \(E_{8} \) and \(E_{10} \) for various values of \(\nu _{2} \). Figure 1 provides the comparison of \(y(x)\) for \(N = 4\) with various values of \(\nu _{2}\), where \(\nu _{2}= 2\), 1.8, 1.7, and 1.6. The same comparison is made for \(N=10\) in Fig. 2, and the comparison of the error function for the present method at \(N=4\) and [65] at \(N = 8\) and 10 is given in Fig. 3 for Example 4.
Comparison of \(y(x)\) for \(N = 4\) with \(\nu _{2}= 2\), 1.8, 1.7, and 1.6 for Example 4
Comparison of \(y(x)\) for \(N = 10\) with \(\nu _{2}= 2\), 1.9, 1.8, and 1.7 for Example 4
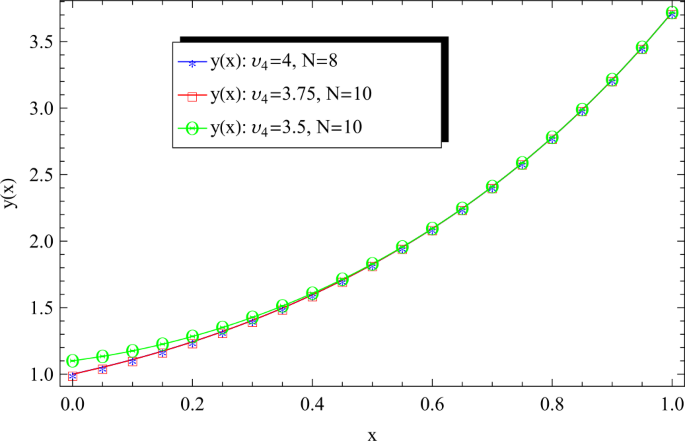
\(y(x)\) for different N and \(\nu _{4}\) values for Example 5
Example 5
Let us assume the fractional integro-differential equation [68, 69]
The subjected conditions are \(y(1)=1+e\), \(y^{\prime }(1)=2e\), \(y^{\prime \prime }(1)=3e\), \(y^{\prime \prime \prime }(1)=4e\), the exact solution of this FIDE is \(y(x)=1+xe^{x}\) when \(\nu _{4}=4\). For solving this challenge, we apply the present scheme for various values of N.
In Table 5, we contribute the numerical results \(y(x_{l})\), for \(N = 9\), of our proposed scheme together with numerical results \(y(x_{l})\), for \(N = 10\), of the Legendre collocation method (LCM) [69] and [68]. It is observed that the proposed scheme reaches the same results of [69] with lower degree of approximation. Moreover, the proposed scheme has superior results with regard to the ADM [66] as shown in [69]. In addition, the numerical results associated with our presented method LCM and generalized differential transform method (GDTM) [67] for \(N = 10\) and \(\nu _{4} = 3.75\) are given in Table 6. As shown in Table 4 of [69], the ADM has very weak approximations with regard to GDTM and LCM. Therefore, we do not consider ADM in Table 6. From this table, we can find that our achieved results are the same as those of LCM, but GDTM results are away from our proposed scheme and LCM results. Achieved evidences confirm the capability of our scheme. For showing the authenticity of the proposed scheme, we depicted the numerical solution \(y(x)\) for various values of \(\nu _{4}\) such as: 3.50, 3.75, and 4. Also, Fig. 5 compares the error function for the present method at \(N=8\), \(N = 9\) and 12 with \(\nu _{4}=4\), and the comparison of the absolute errors for different values of N at \(\nu _{4}=4\) is given in Table 7. The residual error \(E_{10} \) is given in Table 8 for different values of \(\nu _{4} \) as follows: \(3.75, 3.5\).
Comparison of error function for the present method at \(N=8\), \(N = 9\) and 12 for Example 5, where \(\nu _{4}=4\)
Finally, since problem (56) defines on \([0,1]\) the proposed method applied with the Chebyshev nodes (zeros of Chebyshev polynomials) as collocation points. Table 9 compares the absolute errors for different values of N at \(\nu _{4}=4\) using Chebyshev nodes collocation points, namely \(\frac{1}{2} ( 1+\cos \frac{i \pi }{N} ), i=0,1,\ldots,N \). Also, the comparison of the \(L_{2}\) error norm according to (42) using both equally spaced (11) and Chebyshev nodes collocation points is given in Table 10. Comparing Table 7 with Table 9 and the \(L_{2}\) results in Table 10, one finds that the nodes of Chebyshev fall on \([-1,1]\) and they are chosen with the collocation method as collocation points if the problem is also defined in the same interval, and better results will be obtained than any choice of other form of collocation points, and any modification in the nodes to fit the interval of the problem does not give the good results as expected than the original zeros of the Chebyshev polynomials.
5 Conclusion
A numerical study for a generalized form of nonlinear arbitrary order integro-differential equations (GNFIDEs) with linear functional arguments is introduced using Chebyshev series. The suggested equation with its linear functional argument represents a general form of delay, proportional delay, and advanced nonlinear fractional order Fredholm–Volterra integro-differential equations. Additionally, we have presented a general form of the operational matrix of derivatives. The fractional and ordinary order derivatives have been obtained and presented in one general operational matrix. Therefore, the proposed operational matrix represents a kind of unification of ordinary and fractional case. To the best of authors knowledge, there is no other work discussing this point. We have presented many numerical examples that greatly illustrate the accuracy of the presented study to the proposed equation and also show how that the propose scheme is very competent and acceptable.
References
Yang, X.J., Gao, F., Ju, Y.: General Fractional Derivatives with Applications in Viscoelasticity. Academic Press, San Diego (2020)
Subashini, R., Ravichandran, C., Jothimani, K., Baskonus, H.M.: Existence results of Hilfer integro-differential equations with fractional order. Discrete Contin. Dyn. Syst., Ser. S 13(3), 911–923 (2020)
Valliammal, N., Ravichandran, C., Hammouch, Z., Baskonus, H.M.: A new investigation on fractional-ordered neutral differential systems with state-dependent delay. Int. J. Nonlinear Sci. Numer. Simul. 20(7–8), 803–809 (2019)
Jerri, A.: Introduction to Integral Equations with Applications, 2nd edn. Wiley, New York (1999)
Osman, M.S.: New analytical study of water waves described by coupled fractional variant Boussinesq equation in fluid dynamics. Pramana 93(2), 26 (2019)
Al-Ghafri, K.S., Rezazadeh, H.: Solitons and other solutions of \((3+ 1)\)-dimensional space-time fractional modified KdV-Zakharov–Kuznetsov equation. Appl. Math. Nonlinear Sci. 4(2), 289–304 (2019)
Jothimani, K., Kaliraj, K., Hammouch, Z., Ravichandran, C.: New results on controllability in the framework of fractional integrodifferential equations with nondense domain. Eur. Phys. J. Plus 134(9), 441 (2019)
Dehghan, M., Shakeri, F.: Solution of parabolic integro-differential equations arising in heat conduction in materials with memory via He’s variational iteration technique. Int. J. Numer. Methods Biomed. Eng. 26(6), 705–715 (2010)
Ilhan, E., Kiymaz, I.O.: A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 5(1), 171–188 (2020)
Gao, W., Baskonus, H.M., Shi, L.: New investigation of bats-hosts-reservoir-people coronavirus model and application to 2019-nCoV system. Adv. Differ. Equ. 2020(1), 1 (2020)
Yang, X.J., Abdel-Aty, M., Cattani, C.: A new general fractional-order derivative with Rabotnov fractional-exponential kernel applied to model the anomalous heat transfer. Therm. Sci. 23(3 Part A), 1677–1681 (2019)
Xiao-Jun, X.J., Srivastava, H.M., Machado, J.T.: A new fractional derivative without singular kernel. Therm. Sci. 20(2), 753–756 (2016)
Yang, A.M., Han, Y., Li, J., Liu, W.X.: On steady heat flow problem involving Yang–Srivastava–Machado fractional derivative without singular kernel. Therm. Sci. 20(suppl. 3), 717–721 (2016)
Yang, X.J., Feng, Y.Y., Cattani, C., Inc, M.: Fundamental solutions of anomalous diffusion equations with the decay exponential kernel. Math. Methods Appl. Sci. 42(11), 4054–4060 (2019)
Kumar, S., Ghosh, S., Samet, B., Goufo, E.F.: An analysis for heat equations arises in diffusion process using new Yang–Abdel–Aty–Cattani fractional operator. Math. Methods Appl. Sci. 43(9), 6062–6080 (2020)
Kumar, S., Kumar, R., Agarwal, R.P., Samet, B.: A study of fractional Lotka–Volterra population model using Haar wavelet and Adams–Bashforth–Moulton methods. Math. Methods Appl. Sci. 43(8), 5564–5578 (2020)
Kumar, S., Ahmadian, A., Kumar, R., Kumar, D., Singh, J., Baleanu, D., Salimi, M.: An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics 8(4), 558 (2020)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Technical University of Kosice, Solvak Republic (1998)
Kilbas, A.A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)
Gao, W., Veeresha, P., Prakasha, D.G., Novel, B.H.M.: Dynamic structures of 2019-nCoV with nonlocal operator via powerful computational technique. Biology 9(5), 107 (2020)
Atangana, A.: Fractional discretization: the African’s tortoise walk. Chaos Solitons Fractals 130, 109399 (2020)
Yang, X.J.: Advanced Local Fractional Calculus & Its Applications. World Science Publisher, New York (2012)
Yang, X.J., Baleanu, D., Srivastava, H.M.: Local Fractional Integral Transforms and Their Applications. Elsevier, Amsterdam (2015)
Atangana, A.: Blind in a commutative world: simple illustrations with functions and chaotic attractors. Chaos Solitons Fractals 114, 347–363 (2018)
Singh, J., Kumar, D., Hammouch, Z., Atangana, A.: A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 316, 504–515 (2018)
Dehghan, M., Shakourifar, M., Hamidi, A.: The solution of linear and nonlinear systems of Volterra functional equations using Adomian–Pade technique. Chaos Solitons Fractals 39(5), 2509–2521 (2009)
Yusufoğlu, E.: An efficient algorithm for solving integro-differential equations system. Appl. Math. Comput. 192(1), 51–55 (2007)
Javidi, M.: Modified homotopy perturbation method for solving system of linear Fredholm integral equations. Math. Comput. Model. 50(1–2), 159–165 (2009)
Ali, K.K., Cattani, C., Gómez-Aguilarc, J.F., Baleanu, D., Osman, M.S.: Analytical and numerical study of the DNA dynamics arising in oscillator-chain of Peyrard–Bishop model. Chaos Solitons Fractals 139, 110089 (2020)
Arqub, O.A., Osman, M.S., Abdel-Aty, A.H., Mohamed, A.B.A., Momani, S.: A numerical algorithm for the solutions of ABC singular Lane–Emden type models arising in astrophysics using reproducing kernel discretization method. Mathematics 8(6), 923 (2020)
Arikoglu, A., Ozkol, I.: Solutions of integral and integro-differential equation systems by using differential transform method. Comput. Math. Appl. 56(9), 2411–2417 (2008)
Saeedi, H., Moghadam, M.M., Mollahasani, N., Chuev, G.N.: A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order. Commun. Nonlinear Sci. Numer. Simul. 16(3), 1154–1163 (2011)
Zhu, L., Fan, Q.: Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet. Commun. Nonlinear Sci. Numer. Simul. 17(6), 2333–2341 (2012)
Eslahchi, M.R., Dehghan, M., Parvizi, M.: Application of the collocation method for solving nonlinear fractional integro-differential equations. J. Comput. Appl. Math. 257, 105–128 (2014)
Lakestani, M., Saray, B.N., Dehghan, M.: Numerical solution for the weakly singular Fredholm integro-differential equations using Legendre multiwavelets. J. Comput. Appl. Math. 235(11), 3291–3303 (2011)
Lakestani, M., Jokar, M., Dehghan, M.: Numerical solution of nth-order integro-differential equations using trigonometric wavelets. Math. Methods Appl. Sci. 34(11), 1317–1329 (2011)
Fakhar-Izadi, F., Dehghan, M.: The spectral methods for parabolic Volterra integro-differential equations. J. Comput. Appl. Math. 235(14), 4032–4046 (2011)
Sezer, M., Akyüz-Daşcıoglu, A.: A Taylor method for numerical solution of generalized pantograph equations with linear functional argument. J. Comput. Appl. Math. 200(1), 217–225 (2007)
Maleknejad, K., Mirzaee, F.: Numerical solution of integro-differential equations by using rationalized Haar functions method. Kybernetes 35(10), 1735–1744 (2006)
Yang, Y., Chen, Y., Huang, Y.: Spectral-collocation method for fractional Fredholm integro-differential equations. J. Korean Math. Soc. 51(1), 203–224 (2014)
Azin, H., Mohammadi, F., Machado, J.T.: A piecewise spectral-collocation method for solving fractional Riccati differential equation in large domains. Comput. Appl. Math. 38(3), 96 (2019)
Patrício, M.S., Ramos, H., Patrício, M.: Solving initial and boundary value problems of fractional ordinary differential equations by using collocation and fractional powers. J. Comput. Appl. Math. 354, 348–359 (2019)
Hou, J., Yang, C., Lv, X.: Jacobi collocation methods for solving the fractional Bagley–Torvik equation. Int. J. Appl. Math. 50(1), 114–120 (2020)
Ramadan, M.A., Dumitru, B., Highly, N.M.A.: Accurate numerical technique for population models via rational Chebyshev collocation method. Mathematics 7(10), 913 (2019)
Yang, X.J., Gao, F., Ju, Y., Zhou, H.W.: Fundamental solutions of the general fractional-order diffusion equations. Math. Methods Appl. Sci. 41(18), 9312–9320 (2018)
Yang, X.J., Tenreiro Machado, J.A.: A new fractal nonlinear Burgers’ equation arising in the acoustic signals propagation. Math. Methods Appl. Sci. 42(18), 7539–7544 (2019)
Cao, Y., Ma, W.G., Ma, L.C.: Local fractional functional method for solving diffusion equations on Cantor sets. Abstr. Appl. Anal. 2014, Article ID 803693 (2014)
Oğuz, C., Sezer, M.: Chelyshkov collocation method for a class of mixed functional integro-differential equations. Appl. Math. Comput. 259, 943–954 (2015)
Saadatmandi, A., Dehghan, M.: Numerical solution of the higher-order linear Fredholm integro-differential-difference equation with variable coefficients. Comput. Math. Appl. 59(8), 2996–3004 (2010)
Kürkçü, Ö., Aslan, E., Sezer, M.: A numerical approach with error estimation to solve general integro-differential-difference equations using Dickson polynomials. Appl. Math. Comput. 276, 324–339 (2016)
Gülsu, M., Öztürk, Y., Sezer, M.: A new collocation method for solution of mixed linear integro-differential-difference equations. Appl. Math. Comput. 216(7), 2183–2198 (2010)
Yüzbaşı, Ş.: Laguerre approach for solving pantograph-type Volterra integro-differential equations. Appl. Math. Comput. 232, 1183–1199 (2014)
Osman, M.S., Rezazadeh, H., Eslami, M., Neirameh, A., Mirzazadeh, M.: Analytical study of solitons to Benjamin–Bona–Mahony–Peregrine equation with power law nonlinearity by using three methods. UPB Sci. Bull., Ser. A, Appl. Math. Phys. 80(4), 267–278 (2018)
Osman, M.S., Rezazadeh, H., Eslami, M.: Traveling wave solutions for \((3+ 1)\) dimensional conformable fractional Zakharov–Kuznetsov equation with power law nonlinearity. Nonlinear Eng. 8(1), 559–567 (2019)
Yang, X.J.: New non-conventional methods for quantitative concepts of anomalous rheology. Therm. Sci. 23(6B), 4117–4127 (2019)
Yang, X.J.: New general calculi with respect to another functions applied to describe the Newton-like dashpot models in anomalous viscoelasticity. Therm. Sci. 23(6B), 3751–3757 (2019)
Kumar, S., Kumar, R., Cattani, C., Samet, B.: Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals 135, 109811 (2020)
Odibat, Z., Kumar, S.: A robust computational algorithm of homotopy asymptotic method for solving systems of fractional differential equations. J. Comput. Nonlinear Dyn. 14(8), 081004 (2019)
Iakovleva, V., Vanegas, C.J.: On the solution of differential equations with delayed and advanced arguments. Electron. J. Differ. Equ. 13, 57 (2005)
Rus, I.A., Dârzu-Ilea, V.A.: First order functional-differential equations with both advanced and retarded arguments. Fixed Point Theory 5(1), 103–115 (2004)
Liu, Z., Sun, J., Szántó, I.: Monotone iterative technique for Riemann–Liouville fractional integro-differential equations with advanced arguments. Results Math. 63(3–4), 1277–1287 (2013)
Şahin, N., Yüzbaşi, Ş.: Sezer, M.: A Bessel polynomial approach for solving general linear Fredholm integro-differential-difference equations. Int. J. Comput. Math. 88(14), 3093–3111 (2011)
Raslan, K.R., Ali, K.K., Abd El Salam, M.A., Mohamed, E.M.H.: Spectral Tau method for solving general fractional order differential equations with linear functional argument. J. Egypt. Math. Soc. 27(1), 33 (2019)
Ali, K.K., Abd El Salam, M.A., Mohamed, E.M.H.: Chebyshev operational matrix for solving fractional order delay-differential equations using spectral collocation method. Arab J. Basic Appl. Sci. 26(1), 342–352 (2019)
Gürbüz, B., Sezer, M., Güler, C.: Laguerre collocation method for solving Fredholm integro-differential equations with functional arguments. J. Appl. Math. 2014, Article ID 682398 (2014)
El-Wakil, S.A., Elhanbaly, A., Abdou, M.A.: Adomian decomposition method for solving fractional nonlinear differential equations. Appl. Math. Comput. 182(1), 313–324 (2006)
Erturk, V.S., Momani, S., Odibat, Z.: Application of generalized differential transform method to multi-order fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 13(8), 1642–1654 (2008)
Tohidi, E., Ezadkhah, M.M., Shateyi, S.: Numerical solution of nonlinear fractional Volterra integro-differential equations via Bernoulli polynomials. In: Abstract and Applied Analysis 2014 (2014)
Saadatmandi, A., Dehghan, M.: A Legendre collocation method for fractional integro-differential equations. J. Vib. Control 17(13), 2050–2058 (2011)
Yang, X.J.: Local Fractional Functional Analysis & Its Applications. Asian Academic Publisher, Hong Kong (2011)
Yang, X.J.: General Fractional Derivatives: Theory, Methods and Applications. Taylor & Francis Group, New York (2019)
Acknowledgements
The fifth author, Dr Sunil Kumar, would like to acknowledge the financial support received from the Science and Engineering Research Board (SERB), DST Government of India (file no. EEQ/2017/0 0 0385). Prof. B. Samet is supported by Researchers Supporting Project, number (RSP-2020/4), King Saud University, Riyadh, Saudi Arabia.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors carried out the proofs and conceived of the study. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ali, K.K., Abd El Salam, M.A., Mohamed, E.M.H. et al. Numerical solution for generalized nonlinear fractional integro-differential equations with linear functional arguments using Chebyshev series. Adv Differ Equ 2020, 494 (2020). https://doi.org/10.1186/s13662-020-02951-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02951-z