- Research
- Open access
- Published:
Local fractional Newton’s inequalities involving generalized harmonic convex functions
Advances in Difference Equations volume 2020, Article number: 185 (2020)
Abstract
A new auxiliary result based on a three step quadratic kernel utilizing the concepts of local fractional calculus is obtained. Using this new auxiliary result we have several new Newton type inequalities whose power q of local fractional derivative in modulus is a generalized harmonic convex function.
1 Introduction
The following result is well known in the literature as error estimation, Simpson’s second formula.
Theorem 1.1
Let\(\varphi :[c,d]\rightarrow \mathbb{R}\)be a four times continuously differentiable mapping on\((c,d)\)and\(\| \varphi ^{(4)}\| _{\infty }=\sup_{x\in (c,d)}| \varphi ^{(4)}|<\infty \), then
This result is also known as a Newton type of inequality. Since these results have wide applications in the pure and applied sciences, this topic attracted considerable attention of several mathematicians. Some researchers focused on new Simpson type inequalities based on a two step quadratic kernel and Simpson’s second type results based on three step quadratic kernel via different classes of functions. For example, Alomari et al. [4] provided Simpson type inequalities via s-convex functions and they also gave some applications to special means and numerical quadrature rules. Sarikaya et al. [21] gave some new inequalities of Simpson type based on s-convexity and their applications to special means of real numbers. Park in [17] gave some Hadamard and Simpson type results for functions whose second derivatives are s-convex in the second sense. In addition, Gao and Shi [9] obtained new inequalities of Newton type for functions whose absolute values of second derivatives are convex. Inspired by this, some researchers obtained Hermite–Hadamard, Simpson and Simpson’s second type/Newton type inequalities via harmonically convex mappings (see [10, 14, 15]).
Integral equations play an important role in pure and applied mathematics. A large number of initial and boundary value problems related to ordinary and partial differential equations can be transformed into problems of solving some approximate integral equations. However, some initial and boundary value problems are fractal curves, which are everywhere continuous but nowhere differentiable. In these cases, it can be used local fractional theory to handle the fractal and continuously non-differentiable functions, because this theory deal with everywhere continuous but nowhere differentiable functions in fractal space.
Local fractional theory that was introduced by Yang in [27] is used to handle different non-differentiable problems which appear in complex systems of the real-world phenomenon. Specifically, the non-differentiability circumstance in science and engineering was modeled by means of ordinary or partial differential equations including local fractional statements. What is more, local fractional derivatives and integrals are effectively applied many equations such as Fokker–Planck, diffusion and relaxation equation in fractal space, the fractal heat conduction equation and local fractional diffusion equation. We also note that concepts of fractional calculus have many advantages, for example one of the significant advantages of the Caputo fractional derivative is that it allows traditional initial and boundary conditions to be included in the formulation of the problem. On the other side, Fractional calculus have played a significant role in different fields of pure and applied sciences such as mechanics, electricity, chemistry, biology, economics, notably control theory, and signal and image processing etc. Due to this, local fractal theory has received significantly great attention from scientists and engineers. Therewith, these topics are observed a lot of researchers who study in areas such as mathematical physics and applied sciences (for example [25]). For more details, see [25–27]. Furthermore, local fractional versions of some inequalities which have a very significant role in application areas of mathematics are studied by many mathematicians. For instance, Chen established a Hölder inequality and some integral inequalities on fractal space in [6]. In [13], Mo et al. discovered the generalized Hermite–Hadamard inequality for a generalized convex function. Also, generalized Hermite–Hadamard type inequalities for generalized convex functions were presented by Sarikaya and Budak in [19]. New Simpson type integral inequalities involving local fractional integrals were obtained by Sarikaya et al. [20]. Sun, in [22], introduced the concept of generalized harmonically convex functions and obtained Hermite–Hadamard type inequalities. He has also worked on some inequalities on generalization of Ostrowski and Simpson type inequalities for functions whose absolute values of derivatives are generalized harmonically convex in [23]. In addition to these results, Noor et al. deduced several new Hermite–Hadamard inequalities for a new class of convex functions including generalized convex functions and harmonic convex functions in [16]. For some useful and recent studies on fractional calculus and its applications in different fields of mathematics, see [1–3, 5, 7, 8, 11, 12, 18, 24].
The main objective of this paper is to obtain a new auxiliary result based on a three step quadratic kernel by utilizing the concepts of local fractional calculus. With the help of this new auxiliary result we obtain several new integral inequalities of Newton type for functions whose powers of local fractional derivatives in modulus are generalized harmonic convex. The main motivation of this paper is to capture new estimations for generalized convex functions. We expect that the ideas and techniques used in this paper will inspire the interested reader working in the field of inequalities.
2 Preliminaries
In this section, we discuss some preliminary concepts and results which will play significant roles in the development of the main results of the paper.
First of all, we give the set \(\mathbb{R}^{\alpha }\) of real line numbers to describe the definitions of the local fractional derivative and integral. For \(0<\alpha \leq 1\), we have the following α-type sets:
- \(Z^{\alpha }\)::
The α-type set of integer is defined as the set \(\{ 0^{\alpha },\pm 1^{\alpha },\pm 2^{\alpha },\ldots,\pm n^{ \alpha },\ldots \} \).
- \(Q^{\alpha }\)::
The α-type set of the rational numbers is defined as the set \(\{m^{\alpha }= ( \frac{p}{q} ) ^{\alpha }: {p,q\in Z}, {q\neq 0}\}\).
- \(J^{\alpha }\)::
The α-type set of the irrational numbers is defined as the set \(\{m^{\alpha }\neq ( \frac{p}{q} ) ^{\alpha }: {p,q\in Z}, {q\neq 0}\}\).
- \(\mathbb{R}^{\alpha }\)::
The α-type set of the real numbers is defined as the set \(\mathbb{R}^{\alpha }=Q^{\alpha }\cup J^{\alpha }\).
If \(\rho ^{\alpha }\), \(\sigma ^{\alpha }\) and \(\tau ^{\alpha }\) belongs to the set \(\mathbb{R}^{\alpha }\) of real numbers, then
- (1)
\(\rho ^{\alpha }+\sigma ^{\alpha }\) and \(\rho ^{\alpha }\sigma ^{\alpha } \) belongs to the set \(\mathbb{R}^{\alpha }\);
- (2)
\(\rho ^{\alpha }+\sigma ^{\alpha }=\sigma ^{\alpha }+\rho ^{\alpha }= ( \rho +\sigma ) ^{\alpha }= ( \sigma +\rho ) ^{\alpha }\);
- (3)
\(\rho ^{\alpha }+ ( \sigma ^{\alpha }+\tau ^{\alpha } ) = ( \rho +\sigma ) ^{\alpha }+\tau ^{\alpha }\);
- (4)
\(\rho ^{\alpha }\sigma ^{\alpha }=\sigma ^{\alpha }\rho ^{\alpha }= ( \rho \sigma ) ^{\alpha }= ( \sigma \rho ) ^{ \alpha }\);
- (5)
\(\rho ^{\alpha } ( \sigma ^{\alpha }\tau ^{\alpha } ) = ( \rho ^{\alpha }\sigma ^{\alpha } ) \tau ^{\alpha }\);
- (6)
\(\rho ^{\alpha } ( \sigma ^{\alpha }+\tau ^{\alpha } ) = \rho ^{\alpha }\sigma ^{\alpha }+\rho ^{\alpha }\tau ^{\alpha }\);
- (7)
\(\rho ^{\alpha }+0^{\alpha }=0^{\alpha }+\rho ^{\alpha }=\rho ^{ \alpha }\) and \(\rho ^{\alpha }1^{\alpha }=1^{\alpha }\rho ^{\alpha }=\rho ^{\alpha }\).
The definition of the local fractional derivative is given as follows.
Definition 2.1
([27])
A non-differentiable function \(\varphi :\mathbb{R}\rightarrow \mathbb{R}^{\alpha }\),  is called local fractional continuous at
is called local fractional continuous at  , if for any \(\varepsilon >0\), there exists \(\delta >0\), such that
, if for any \(\varepsilon >0\), there exists \(\delta >0\), such that

holds for  , where \(\varepsilon ,\delta \in \mathbb{R}\). If
, where \(\varepsilon ,\delta \in \mathbb{R}\). If  is local continuous on the interval \(( c,d ) \), we denote
is local continuous on the interval \(( c,d ) \), we denote  .
.
Definition 2.2
([27])
The local fractional derivative of  of order α at
of order α at  is defined by
is defined by

where  .
.
If there exists  for any
for any  , then we denote \(\varphi \in D_{(k+1)\alpha }(I)\), where \(k=0,1,2,\ldots \) .
, then we denote \(\varphi \in D_{(k+1)\alpha }(I)\), where \(k=0,1,2,\ldots \) .
The definition and some properties of the local fractional integral that we will use throughout this article are defined as follows.
Definition 2.3
([27])
Let  . Then the local fractional integral is defined by
. Then the local fractional integral is defined by

with \(\Delta x_{j}=x_{j+1}-x_{j}\) and \(\Delta x=\max \{ \Delta x_{1},\Delta x_{2},\ldots,\Delta x_{N-1} \} \), where \([ x_{j},x_{j+1} ] \), \(j=0,\ldots,N-1\) and \(c=x_{0}< x_{1}<\cdots<x_{N-1}<x_{N}=d\) is a partition of the interval \([ c,d ] \).
Here, it follows that  if \(c=d\) and
if \(c=d\) and  if \(c< d\). If, for any
if \(c< d\). If, for any  , there exists
, there exists  , then we denote
, then we denote  .
.
Lemma 2.1
([27])
-
(i)
(Local fractional integration is anti-differentiation) Suppose that
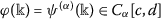 , then we have
, then we have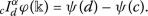
-
(ii)
(Local fractional integration by parts) Suppose that
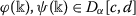 and
and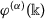 ,
, 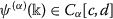 , then we have
, then we have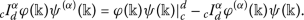
In addition, we ought to give some properties of the local fractional derivative to use in the change of the variable in the integrals.
Lemma 2.2
([26])
Suppose that and
and , then, for\(0<\alpha \leq 1\), we have aα-differential form
, then, for\(0<\alpha \leq 1\), we have aα-differential form

Lemma 2.3
([26])
LetIbe an interval, \(\varphi ,\psi :I\subset R\rightarrow R^{\alpha }\) (\(I^{\circ }\)is the interior ofI) and such that\(\varphi ,\psi \in D_{\alpha }(I^{\circ })\). Then we have
such that\(\varphi ,\psi \in D_{\alpha }(I^{\circ })\). Then we have

Lemma 2.4
([27])
We have
-
(i)
 ;
; -
(ii)
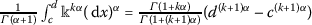 , \(k\in \mathbb{R}\).
, \(k\in \mathbb{R}\).
The class of generalized harmonic convex function which will be examined in this paper is defined as follows.
Definition 2.4
([22])
Let \(\varphi :I\subset \mathbb{R}\setminus \{0\} \rightarrow \mathbb{R}^{\alpha }\). For any \(c,d\in I\) and  , if the inequality
, if the inequality

holds, then φ is called a generalized harmonic convex function on I.
Chen [6] presented the generalized Hölder inequality on fractal space as follows.
Theorem 2.5
Let\(\varphi (x)\), \(\psi (x)\in C_{\alpha }(c,d)\), \(p>1\), \(\frac{1}{p}+\frac{1}{q}=1\). Then
3 Results and discussions
In this section, we first give an auxiliary result involving local factional integral and then we use this result to obtain new Newton type inequalities via generalized harmonic convex functions.
Lemma 3.1
Let\(\varphi :I^{\circ }\subset \mathbb{R}\rightarrow \mathbb{R}^{\alpha }\)be a function such that\(\varphi \in D_{\alpha }(I^{\circ })\)and\(\varphi ^{(\alpha )}\in C_{\alpha }[c,d]\), where\(I^{\circ }\)is the interior of\(I\subset \mathbb{R}\setminus \{0\}\). Then, for all\(x\in {}[ c,d]\), we have

where is defined by
is defined by

Proof
From the definition of  , we have
, we have

Applying the local fractional integration by parts to the first integral in the right side of (3.2), we find that

Combining the resulting identities after calculating the other integrals in (3.2), from the property of fractal space \(c^{\alpha }+d^{\alpha }=(c+d)^{\alpha }\), it follows that

Finally, if we use the change of the variable  and from
and from  , then we obtain the desired equality (3.1) which completes the proof. □
, then we obtain the desired equality (3.1) which completes the proof. □
Remark 3.1
If we take \(\alpha =1\), then Lemma 3.1 collapses to the previous well-known result obtained by Noor et al. in [14].
Theorem 3.2
Let\(\varphi :I^{\circ }\subset \mathbb{R}\rightarrow \mathbb{R}^{\alpha }\)be a function such that\(\varphi \in D_{\alpha }(I^{\circ })\)and\(\varphi ^{(\alpha )}\in C_{\alpha }[c,d]\)where\(I^{\circ }\)is the interior of\(I\subset \mathbb{R}\setminus \{0\}\). If\(|\varphi ^{(\alpha )}|^{q}\)is a generalized harmonic convex function for\(1\leq q \), then one has

where
and
Proof
Taking the modulus in Lemma 3.1 and using the definition of  , we have
, we have

If we also apply the power mean inequality to integrals in the right side of (3.5), and using the fact that \(|\varphi ^{(\alpha )}|^{q}\) is generalized harmonic convex on \([c,d]\), we have

From the Lemma 2.4, it is easy to see that



On the other side, using the change of the variable by considering the Lemmas 2.3 and 2.2, one can obtain

Now, letting \(\frac{1}{x^{2q-2}}=u\) and from \(\frac{1}{x^{(2q-1)\alpha }}(\mathrm{d}x)^{\alpha }=\frac{1}{(2-2q)^{\alpha }}(\mathrm{d}u)^{ \alpha }\), we get
and
Letting \(\frac{1}{x^{2q-1}}=u\) and from \(\frac{1}{x^{2q\alpha }}(\mathrm{d}x)^{\alpha }=\frac{1}{(1-2q)^{\alpha }}(\mathrm{d}u)^{\alpha }\), we have
and
Letting \(\frac{1}{x^{2q-3}}=u\) and from  , we have
, we have
and
Substituting the equalities (3.11)–(3.16) in (3.10), one has

If we similarly calculate the other integrals in (3.6) and later substitute the resulting identities and the equalities (3.7)–(3.9) in (3.6), then we attain the desired inequality (3.4). The proof is thus completed. □
Theorem 3.3
Let\(\varphi :I^{\circ }\subset \mathbb{R}\rightarrow \mathbb{R}^{\alpha }\)be a function such that\(\varphi \in D_{\alpha }(I^{\circ })\)and\(\varphi ^{(\alpha )}\in C_{\alpha }[c,d]\)where\(I\subset \mathbb{R}\setminus \{0\}\). If\(|\varphi ^{(\alpha )}|^{q}\)is a generalized harmonic convex function for\(p>1\), \(\frac{1}{p}+\frac{1}{q}=1\), then one has

Proof
If we apply Hölder’s inequality to the inequality (3.5), because of the generalized harmonic convexity of \(|\varphi ^{(\alpha )}|^{q}\), we get

Using the change of the variable by considering the Lemmas 2.3 and 2.2, one can obtain

and

From Lemma 2.4, one can easily see that

Similarly, we have

Thus, the proof is completed. □
Remark 3.2
For suitable and appropriate choices of α and q, one can obtain new and well-known results.
References
Agarwal, P., Jleli, M., Samet, B.: Fixed Point Theory in Metric Spaces: Recent Advances and Applications, Springer, Berlin (2019)
Agarwal, P., Mdallal, Q.A., Cho, Y.J., Jain, S.: Fractional differential equations for the generalized Mittag-Leffler function. Adv. Differ. Equ. 2018, 58 (2018). https://doi.org/10.1186/s13662-018-1500-7
Agarwal, P., Restrepo, J.E.: An extension by means of ω-weighted classes of the generalized Riemann–Liouville k-fractional integral inequalities. J. Math. Inequal. 14(1), 33–44 (2020)
Alomari, M.W., Darus, M., Dragomir, S.S.: New inequalities of Simpson’s type for s-convex functions with applications. RGMIA Res. Rep. Collect. 12(4), Article ID 9 (2009) Online: http://ajmaa.org/RGMIA/v12n4.php
Atangana, A., Aguilar, J.F.G.: Numerical approximation of Riemann–Liouville definition of fractional derivative: from Riemann–Liouville to Atangana–Baleanu. Numer. Methods Partial Differ. Equ. 34(5), 1502–1523 (2018). https://doi.org/10.1002/num.22195
Chen, G.-S.: Generalizations of Hölder’s and some related integral inequalities on fractal space. J. Funct. Spaces Appl. 2013, Article ID 198405 (2013)
Delgado, V.F.M., Aguilar, J.F.G., Jimenez, R.F.E.: Fractional conformable attractors with low fractality. Math. Methods Appl. Sci. 41(16), 6378–6400 (2018). https://doi.org/10.1002/mma.5146
Delgado, V.F.M., Aguilar, J.F.G., Jimenez, R.F.E., Hernández, M.A.T.: Fractional conformable derivatives of Liouville–Caputo type with low-fractionality. Physica A (2018). https://doi.org/10.1016/j.physa.2018.03.018
Gao, S., Shi, W.: On new inequalities of Newton’s type for functions whose second derivatives absolute values are convex. Int. J. Pure Appl. Math. 74(1), 33–41 (2012)
Iftikhar, S., Kumam, P., Erden, S.: Newton’s type integral inequalities via local fractional integrals. Fractals (2020, in press). https://doi.org/10.1142/S0218348X20500371
Jain, S., Mehrez, K., Baleanu, D., Agarwal, P.: Certain Hermite–Hadamard inequalities for logarithmically convex functions with applications. Mathematics 7, 163 (2019). https://doi.org/10.3390/math7020163
Mehrez, K., Agarwal, P.: New Hermite–Hadamard type integral inequalities for convex functions and their applications. J. Comput. Appl. Math. 350, 274–285 (2019)
Mo, H., Sui, X., Yu, D.: Generalized convex functions on fractal sets and two related inequalities. Abstr. Appl. Anal. 2014, Article ID 636751 (2014)
Noor, M.A., Noor, K.I., Iftikhar, S.: Some Newton’s type inequalities for harmonic convex functions. J. Adv. Math. Stud. 9(1), 7–16 (2016)
Noor, M.A., Noor, K.I., Iftikhar, S.: Newton inequalities for p-harmonic convex functions. Honam Math. J. 40(2), 239–250 (2018)
Noor, M.A., Noor, K.I., Iftikhar, S., Awan, M.U.: Fractal integral inequalities for harmonic convex functions. Appl. Math. Inf. Sci. 12(4), 831–839 (2018)
Park, J.: Hermite and Simpson-like type inequalities for functions whose second derivatives in absolute values at certain power are s-convex. Int. J. Pure Appl. Math. 78, 587–604 (2012)
Perez, J.E.S., Aguilar, J.F.G., Baleanu, D., Tchier, F.: Chaotic attractors with fractional conformable derivatives in the Liouville–Caputo sense and its dynamical behaviors. Entropy 20, 384 (2018). https://doi.org/10.3390/e20050384
Sarikaya, M.Z., Budak, H.: On generalized Hermite–Hadamard inequality for generalized convex function. RGMIA Res. Rep. Collect. 18, Article 64, 15 pp. (2015)
Sarikaya, M.Z., Budak, H., Erden, S.: On new inequalities of Simpson’s type for generalized convex function. Korean J. Math. 27(2), 277–293 (2019)
Sarikaya, M.Z., Set, E., Özdemir, M.E.: On new inequalities of Simpson’s type for s-convex functions. Comput. Math. Appl. 60, 2191–2199 (2010)
Sun, W.: Generalized harmonically convex functions on fractal sets and related Hermite–Hadamard type inequalities. J. Nonlinear Sci. Appl. 10(11), 5869–5880 (2017)
Sun, W.: On generalization of some inequalities for generalized harmonically convex functions via local fractional integrals. Quaest. Math. 42(9), 1159–1183 (2019)
Tomar, M., Agarwal, P., Choi, J.: Hermite–Hadamard type inequalities for generalized convex functions on fractal sets style. Bol. Soc. Parana. Mat. 38(1), 101–116 (2020)
Yang, J., Baleanu, D., Yang, X.J.: Analysis of fractal wave equations by local fractional Fourier series method. Adv. Math. Phys. 2013, Article ID 632309 (2013)
Yang, X.J.: Local Fractional Functional Analysis and Its Applications. Asian Academic Publisher Limited, Hong Kong (2011)
Yang, X.J.: Advanced Local Fractional Calculus and Its Applications. World Science, New York (2012)
Acknowledgements
Authors would like to thank the editor and anonymous referee for their valuable comments and suggestions. Moreover, the first author, Dr. Iftikhar Sabah would like to thank the Postdoctoral Fellowship from King Mongkut’s University of Technology Thonburi (KMUTT), Thailand.
Availability of data and materials
Not applicable.
Funding
The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Author information
Authors and Affiliations
Contributions
The main idea of this paper was proposed by PK and SE. SI and MUA prepared the manuscript initially and performed all the steps of the proofs in this research. All authors worked jointly and contributed equally. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iftikhar, S., Erden, S., Kumam, P. et al. Local fractional Newton’s inequalities involving generalized harmonic convex functions. Adv Differ Equ 2020, 185 (2020). https://doi.org/10.1186/s13662-020-02637-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02637-6
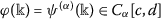 , then we have
, then we have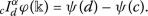
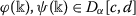 and
and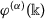 ,
, 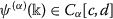 , then we have
, then we have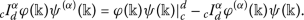
 ;
;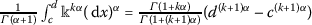 ,
,