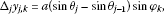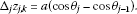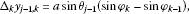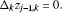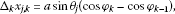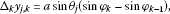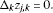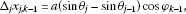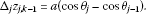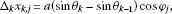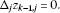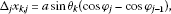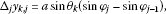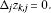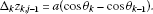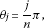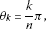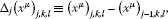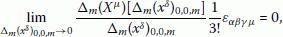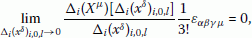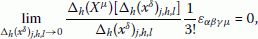- Research
- Open access
- Published:
The divergence theorem of a triangular integral
Advances in Difference Equations volume 2012, Article number: 168 (2012)
Abstract
This divergence theorem of a triangular integral demands the antisymmetric symbol to derive the inner product of the nabla and a vector. Replacing a cuboid (a rectangular solid) by a tetrahedron (a triangular pyramid) as the finite volume element, a single limit is only demanded for triple sums in our theory of a triple integral. The divergence theorem of a triangular integral is derived by substituting the total differentials into our new method of a triangular integral. We thus infer that our new method of a triangular integral must be the inverse operation of the total differential.
1 Introduction
Suppose there are three partially differentiable functions , and of the three variables x, y and z in the 3D space. The divergence theorem in the 3D space is conventionally formulated as

where D is a domain of the integral and ∂D is its surface area. The left-hand side of (1.1) is conventionally defined as

where the increments , and are respectively introduced as , and . The right-hand side of (1.1) is conventionally defined as

where the partial increments , and are respectively introduced as , and . The conventional triple integral demands triple limits at infinities and and of triple independent sums and and of rectangularly divided volumes [1, 2]. We name this conventional triple integral as the rectangular integral for later discussion. In the divergence theorem of the conventional rectangular integral as shown in (1.1), the inner product of the nabla and a vector , i.e.,
explicitly appears as an integrand shown in (1.3).
Meanwhile, the total differential is widely used even in the exterior derivative [3]. However, it is not known how to derive the divergence theorem (1.1) by substituting the total differentials into an integral formula based on the conventional rectangular triple integral method. Replacing the integrand from a scalar function to a tensor function, we may derive the divergence theorem by substituting the total differentials into an integral formula. It depends how we define a new kind of triple integral. We may introduce a new kind of the triangular triple integral by the following two properties:
-
1.
replacing a cuboid (a rectangular solid) by a tetrahedron (a triangular pyramid);
-
2.
replacing triple limits of independent triple sums by a single limit of dependent triple sums.
We name our new method as a triangular integral in contrast with the conventional rectangular integral. Our new method of a triangular double integral was proposed in the previous paper [4], where a rectangle is replaced by a triangle as a finite area element. Our new method of a triangular double integral is extended to triangular triple and quadruple integrals in this paper. Our triangular triple integral is possible to be formulated in the method of a single limit of triple sums. As the curl theorem was discussed by our new method of an integral in the previous paper [4], the divergence theorem is discussed by our new method of an integral in this paper.
The idea of a triangular element was already introduced in the finite element method [5]. However, the triangle is the fundamental element of an integral in our triangular integral theory.
First of all, a triangular integral on the 2D plane is briefly reviewed for simplicity. The total increments (2.33) are substituted into (2.32) to derive (2.31). Combining (2.31) with the antisymmetric finite line element vector in (2.26), we obtain (2.37). In the case of in (2.38), it is reduced to be the divergence theorem of a triangular integral on the 2D plane (2.36).
Next, a triangular integral is applied in the 3D space, where a cuboid (a rectangular solid) is replaced by a tetrahedron (a triangular pyramid) as the finite volume element. Our triangular triple integral only demands a single limit of triple dependent sums and and for tetrahedrally divided volumes in (3.120). We show an example in the case of a sphere. The surface area of the sphere is calculated by the limit at infinity of the finite element method based on our triangular integral. Approximate values and their graph by this finite element method are shown in the case of the sphere. The divergence theorem of a triangular integral in the 3D space (3.119) is derived by calculating double dependent sums (3.95). Total increments (3.108) and (3.109) are substituted into (3.107) to derive (3.106) as the first term of (3.95). In the similar manner, (3.110) is also derived as the second term of (3.95). Combining (3.106) with the upper-right finite area element vector in (3.86) and combining (3.110) with the lower-left finite area element vector in (3.92), we obtain (3.120). In the case of a closed 2D surface (3.121), i.e., (3.118), it is reduced to be the main theorem (3.119) by the limit at infinity . However, the antisymmetric symbol is demanded to derive the inner product of the nabla and a vector (1.4) from the divergence theorem (3.119) based on our new method of a triangular integral, since it only implicitly appears as an integrand.
Finally, our method of a triangular integral is extended in the 4D time-space. It is apparent that the quadruple integral is necessary for the variational principle in the 4D time-space in physics. As the curl theorem in the 4D time-space based on our triangular integral was derived in the previous paper [4], the divergence theorem of a triangular integral in the 4D time-space (4.67) is also derived in this paper.
This paper is structured as follows. Section 2 is the preparatory part, Section 3 is the main part and Section 4 is the additional part of this paper. In Section 2, we briefly derive the divergence theorem on the 2D plane. In Section 3, we develop a theory of a scalar triple product integral by a single limit of triple sums of tetrahedrally divided volumes and derive the divergence theorem in the 3D space. In Section 4, we formulate a theory of an antisymmetric quadruple integral by a single limit of quadruple sums of hyper-triangularly divided hyper-volumes and derive the divergence theorem in the 4D time-space.
2 Integral on the 2D plane
The divergence theorem of a triangular integral on the 2D plane in component representation is shown in Section 2.1 and that in tensor representation is shown in Section 2.2.
Let be a piecewise smooth curve of the equation on the xy-plane, expressed in the Cartesian coordinates . Assume there are two fixed points of and . Suppose there is a sequence of points on , where the initial and the terminal points are respectively and .
2.1 The divergence theorem of a triangular integral on the 2D plane in component representation
For a triangular double integral, the increments of and for are denoted as follows:


Assume there are two partially differentiable functions and of the two variables x and y on the Cartesian coordinates of the 2D plane. Suppose there is a set of sequences . The total increments of for are denoted as
Furthermore, the increments of and for are denoted as follows:


The partial increments of for are denoted as


Lemma 1 Let be a partially differentiable function with respect to x and y. The following holds:
for .
Proof Using (2.3), for is disintegrated into
Using (2.6) and (2.7), in (2.3) is modified to be
Substituting (2.10) into (2.9), we obtain (2.8). Q.E.D.
Lemma 2 Let be a partially differentiable function with respect to x and y. The following holds:
for .
Proof In the similar manner, we obtain (2.11). Q.E.D.
Definition 1 A single integral on the 2D plane in component representation is defined in the case of a piecewise smooth curve of the equation by the formula
where and .
Our triangular double integral and the divergence theorem of a triangular integral on the 2D plane in component representation are shown as follows.
Definition 2 A triangular double integral, integrands of which are partial differentials on the 2D plane in component representation , is defined in the case of a piecewise smooth curve of the equation by the formula

where and .
Theorem 1 Assume ∂D is a piecewise smooth curve of the equation on the xy-plane, expressed in the Cartesian coordinates . Assume D is the region inside and on ∂D. Let and be partially differentiable functions with respect to x and y in D. In the case of a closed integral path, i.e., , the divergence theorem of a triangular integral on the 2D plane holds:

Proof Combining (2.8) with and (2.11) with for the sum of , the following holds:
The limit of (2.15) at infinity is expressed as
by Definitions 1 and 2, where and . In the case of
(2.16) is reduced to be (2.14). The coincidence of the initial and the terminal points, i.e., satisfies this condition (2.17). Q.E.D.
Since the inner product of the nabla and a vector does not explicitly appear in Theorem 1, the corollary shown below is necessary to be derived. Infinitesimal area element is introduced as .
Corollary 1 In the case of
where is a given function, the following holds:
Proof Using Theorem 1, the left-hand side of (2.18) is modified to be

Therefore, the following hold:


Combining (2.21) with (2.22), they are reduced to be (2.19). Q.E.D.
Remark In an explicit differential form, the following holds:
However, (2.23) does not hold as an integrand in our triangular integral.
2.2 The divergence theorem of a triangular integral on the 2D plane in tensor representation
Before expressing the following formulae in tensor representation, the antisymmetric symbol on the 2D plane is introduced as
On the 2D plane, holds for , where the index is summed over . also holds, where the indices are summed over .
Denoting and , the increments of for and are expressed as
Using the antisymmetric symbol shown in (2.24), the antisymmetric finite line element vector is introduced as
for and , where is α-component of , and the index is summed over . We denote and in the following. Assume there are two partially differentiable functions of two variables for on the Cartesian coordinates of the 2D plane. The total increments of for and are denoted as
The increments of for and are expressed as
The partial increments of for and are denoted as


Lemma 3 Let be partially differentiable functions with respect to for . The following holds:
for and , where the index is summed over .
Proof Using (2.27), for and is disintegrated into
Using (2.29) and (2.30), for and in (2.27) is modified to be
where the index is summed over . Substituting (2.33) into (2.32), we obtain (2.31). Q.E.D.
Definition 3 A single integral on the 2D plane in tensor representation is defined in the case of a piecewise smooth curve of the equation by the formula
where and and the index is summed over .
Our triangular double integral and the divergence theorem of a triangular integral on the 2D plane in tensor representation are shown as follows.
Definition 4 A triangular double integral, integrands of which are partial differentials on the 2D plane in tensor representation , is defined in the case of a piecewise smooth curve of the equation by the formula,
where and and the indices are summed over .
Theorem 2 Assume ∂D is a piecewise smooth curve of the equation on the xy-plane, expressed in the Cartesian coordinates . Assume D is the region inside and on ∂D. Let and be partially differentiable functions with respect to and in D. In the case of a closed integral path, i.e., , the divergence theorem of a triangular integral on the 2D plane holds:
where and the indices are summed over .
Proof Combining (2.31) with the antisymmetric finite line element vector in (2.26) for the sum of , the following holds:

where the indices are summed over . The limit of (2.37) at infinity is expressed as
by Definitions 3 and 4, where , , and the indices are summed over . In the case of
where the indices are summed over , (2.38) is reduced to be (2.36). The coincidence of the initial and the terminal points, i.e., satisfies the condition (2.39). Q.E.D.
Infinitesimal area element is introduced as , where the index is summed over .
Corollary 2 In the case of
where is a given function and the index is summed over , the following holds:
Proof Using Theorem 2, the left-hand side of (2.40) is modified to be
where the indices are summed over . In order to hold (2.42) for any value of integral variables, the following formula is demanded:
for , where the index is summed over . Multiplying to the both sides of the formula (2.43), it is reduced to be the differential equation (2.41). Q.E.D.
Remark and are respectively replaced by and in the case they are explicit differential forms, but not as integrand.
3 Integral in the 3D space
As the curl theorem in the 3D space was derived in the previous paper [4], the divergence theorem of a triangular integral in the 3D space is derived in this paper.
Let be a piecewise smooth surface of the equation in the -space, expressed in the Cartesian coordinates . Suppose there are two kinds of double sequences of points and for and on . The surface area of the sphere is approximated as a finite number of pieces of the plane. Dividing these pieces of plane by upper-right part and lower-left one, we may express them as the two kinds of double sums of areas. Each piece of the plane is an isosceles trapezium. It is divided into two triangles, upper-right and lower-left ones.
3.1 Two kinds of finite area element vectors in the 3D space in component representation
-
1.
The upper-right finite area element vector .
Let the coordinates of O, , , and respectively be , , , and for and . An upper-right finite area element vector for and is disintegrated into two parts,
where and are respectively introduced as


Two kinds of the finite area element of an upper-right piece. Two kinds of finite area element vectors and in (3.1) shown in Figure 1 are introduced as </p><p> </p><p> for and .
</p><p> for and .
-
2.
The lower-left finite area element vector .
Let the coordinates of O, , , and respectively be , , , and for and . A lower-left finite area element vector for and is disintegrated into two parts,
where and are respectively introduced as


Two kinds of the finite area element of a lower-left piece. Two kinds of finite area element vectors and in (3.4) shown in Figure 3 are introduced as </p><p> </p><p> for and .
</p><p> for and .
Component representations of , , and are shown in the following.
-
1.
The upper-right finite area element vector .
-
(a)
Component representation of .
in (3.2) for and is expressed as
Denoting , and , we introduce and for and and as


The concrete forms of , , , , and are respectively shown in (3.44), (3.45), (3.46), (3.47), (3.48) and (3.49) in the case of the sphere. Substituting (3.8) and (3.9) into (3.7), we modify the x-component of for and as
In the similar manner, we respectively modify the y- and the z-components of (3.7) for and as


-
(b)
Component representation of .
in (3.3) for and is expressed as
We also introduce and for and and as


The concrete forms of , , , , and are respectively shown in (3.50), (3.51), (3.52), (3.53), (3.54) and (3.55) in the case of the sphere. Substituting (3.14) and (3.15) into (3.13), we modify the x-component of for and as
In the similar manner, we respectively modify the y- and the z-components of (3.13) for and as


-
2.
The lower-left finite area element vector .
-
(a)
Component representation of .
In the similar manner, we respectively introduce and for and and as


The concrete forms of , , , , and are respectively shown in (3.61), (3.62), (3.63), (3.64), (3.65) and (3.66) in the case of the sphere. Interchanging j and k in (3.2), we immediately obtain (3.5). In the similar manner, interchanging j and k in (3.10), (3.11) and (3.12) for and , we respectively obtain



-
(b)
Component representation of .
In the similar manner, we respectively introduce and for and and as


The concrete forms of , , , , and are respectively shown in (3.67), (3.68), (3.69), (3.70), (3.71) and (3.72) in the case of the sphere. Interchanging j and k in (3.3), we immediately obtain (3.6). In the similar manner, interchanging j and k in (3.16), (3.17) and (3.18) for and , we respectively obtain



3.2 The sum of surface areas consisting of triangles
Let us divide the area of the 2D surface of a 3D solid into areas, i.e., n-division for longitudinal direction and n-division for latitudinal direction. The longitudinal and latitudinal directions of the surface are divided by the same number n for a single limit. The sum of divided areas is expressed as . It is separated into two parts, one is the upper-right part and the other is the lower-left part. The diagonal components are subtracted from the sum of the upper-right and the lower-left parts since they are overlapped.
Proposition 1 Let be a sum of divided areas of the 2D surface of a 3D solid. is expressed as
where the upper-right finite area element vector and the lower-left one are divided areas of the 2D surface and and are corresponding unit normal vectors of respective divided areas.
Proof is introduced as
As shown in Figures 5 and 6, the upper-right components of in (3.30), including the diagonal ones,are expressed as

As shown in Figures 7 and 8, the lower-left components of in (3.30), including the diagonal ones,are expressed as

Combining (3.31) with (3.32) and subtracting the diagonal components, we obtain (3.29). Q.E.D.
Expanded form of the upper-right pieces of a divided area. This is an expanded form of the upper-right piece of a divided area of the surface of the sphere shown in Figure 5.
Expanded form of the lower-left pieces of a divided area. This is an expanded form of the lower-left piece of a divided area of the surface of the sphere shown in Figure 7.
The area S of the surface of the 3D solid is defined as the limit of at infinity , i.e.,
Proposition 2 The area S of the 2D surface of the 3D solid in is expressed as
under the condition of
where the upper-right finite area element vector and the lower-left one are divided areas of the 2D surface and and are corresponding unit normal vectors of respective divided areas.
Proof Substituting (3.29) into (3.33), we obtain a formula of the total area S as (3.34) under the condition of (3.35). Q.E.D.
3.3 Surface area of the sphere
The Cartesian coordinates are transformed into the spherical coordinates as



The simple case of a sphere is considered, for example, , where . A kind of spherical sequence is introduced in order to sweep all the surfaces of the sphere. The following two sets of notations, for the upper-right finite area element vector and for the lower-left one are introduced here.
-
1.
The upper-right finite area element vector , expressed in terms of for and .
The normal vector is a unit vector , the direction of which is the same as that from the original point to a point on the surface in the case of the sphere,
for and , as shown in Figure 1. In the case of , has the following components of
for and and . The Cartesian coordinates of the upper-right finite area element vector for and are written as



-
(a)
Applying (3.41), (3.42) and (3.43) to (3.8) for , respectively, we obtain
 (3.44)
(3.44)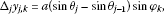 (3.45)
(3.45)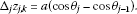 (3.46)
(3.46) -
(b)
Applying (3.41), (3.42) and (3.43) to (3.9) for , respectively, we obtain
 (3.47)
(3.47)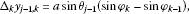 (3.48)
(3.48)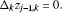 (3.49)
(3.49) -
(c)
Applying (3.41), (3.42) and (3.43) to (3.14) for , respectively, we obtain
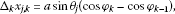 (3.50)
(3.50)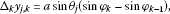 (3.51)
(3.51)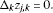 (3.52)
(3.52) -
(d)
Applying (3.41), (3.42) and (3.43) to (3.15) for , respectively, we obtain
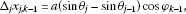 (3.53)
(3.53) (3.54)
(3.54)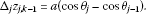 (3.55)
(3.55) -
2.
The lower-left finite area element vector , expressed in terms of for and .
The normal vector is a unit vector , the direction of which is the same as that from the original point to a point on the surface in the case of the sphere,
for and , as shown in Figure 3. In the case of , has the following components of
for and and . The Cartesian coordinates of the lower-left finite area element vectors for and are written as



-
(a)
Applying (3.58), (3.59) and (3.60) to (3.19) for , respectively, we obtain
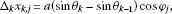 (3.61)
(3.61) (3.62)
(3.62) (3.63)
(3.63) -
(b)
Applying (3.58), (3.59) and (3.60) to (3.20) for , respectively, we obtain
 (3.64)
(3.64) (3.65)
(3.65)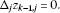 (3.66)
(3.66) -
(c)
Applying (3.58), (3.59) and (3.60) to (3.24) for , respectively, we obtain
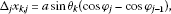 (3.67)
(3.67)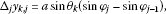 (3.68)
(3.68)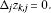 (3.69)
(3.69) -
(d)
Applying (3.58), (3.59) and (3.60) to (3.25) for , respectively, we obtain
 (3.70)
(3.70) (3.71)
(3.71)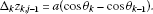 (3.72)
(3.72)
Example 1 The domain of θ is and that of φ is . The surface area of the sphere is divided into two parts as follows.
-
1.
For the upper-right finite area element vector, and are respectively introduced as
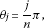 (3.73)
(3.73)

for and , as shown in Figure 2. The concrete increments are shown in the first part of Appendix A. Using (3.10), (3.11), (3.12), (3.16), (3.17) and (3.18), we obtain the upper-right area as
The calculations in detail are shown in the first part of Appendix B in the case of .
-
2.
For the lower-left finite area element vector, and are respectively introduced as
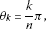 (3.76)
(3.76)

for and , as shown in Figure 4. The concrete increments are shown in the second part of Appendix A. Using (3.21), (3.22), (3.23), (3.26), (3.27) and (3.28), we obtain the lower-left area as
The calculations in detail are shown in the second part of Appendix B in the case of .
Substituting (3.75) and (3.78) into (3.34), we obtain the surface area of the sphere as
We thus obtained the value of the surface area of the sphere by calculating it as the sum of triangles. This calculation is the limit at infinity of the finite element method. Using formula manipulation software, the approximate values according to the finite element method are calculated in Table 1 and their graph is plotted in Figure 9.
Convergence of the two kinds of approximate values of the surface areas of the sphere. Let be a sum of divided areas of the 2D surface of a 3D solid. is expressed as </p><p> </p><p> where two kinds of finite area element vectors and are divided areas of the 2D surface and and are corresponding unit normal vectors of respective divided area elements. As , </p><p>
</p><p> where two kinds of finite area element vectors and are divided areas of the 2D surface and and are corresponding unit normal vectors of respective divided area elements. As , </p><p> </p><p> coincides with at infinity .
</p><p> coincides with at infinity .
3.4 Two kinds of finite area element vectors in the 3D space in tensor representation
Before expressing the following formulae in tensor representation, the antisymmetric symbol in the 3D space is introduced as
In the 3D space, holds for , where the indices are summed over . also holds, where the indices are summed over .
-
1.
The upper-right finite area element vector for and and is disintegrated into
(3.81)
where , and are respectively μ-components of , and . Using the antisymmetric symbol shown in (3.80), (3.2) and (3.3) for and and are respectively written as


where the indices are summed over . Here, and for and and are respectively expressed as


where the indices are summed over . Substituting (3.84) and (3.85) into (3.81) for and and , we may modify it as
where the indices are summed over .
-
2.
The lower-left finite area element vector for and and is also disintegrated into
(3.87)
where , and are respectively μ-components of , and . Using the antisymmetric symbol shown in (3.80), (3.5) and (3.6) for and and are respectively written as


where the indices are summed over . Here, and for and and are respectively expressed as


where the indices are summed over . Substituting (3.90) and (3.91) into (3.87) for and and , we may modify it as
where the indices are summed over .
3.5 The divergence theorem of a triangular integral in the 3D space
In the following subsection, we prepare definitions and notations for extending Theorem 2 and Corollary 2 in the 3D space. Assume there are three functions , and of the three variables x, y and z in the Cartesian coordinates of the 3D space. Suppose there are two sets of double dependent sequences (3.93) and (3.94) as follows. Denoting , and , the two sets of integrand vectors and for and and are expressed as


For integrand vectors and , we introduce the following double dependent sums:

where the index is summed over . In order to prove Theorem 3, and are respectively modified in Lemmata 4 and 5.
-
1.
The total increments of for and are denoted as
(3.96)
The increments of for and are denoted as
The partial increments of for and are denoted as



-
2.
The total increments of for and are denoted as
(3.101)
The increments of for and are denoted as
The partial increments of for and are denoted as



Lemma 4 In the case of for and and , the following holds:
where the index is summed over .
Proof Using (3.96) and (3.101), for and and is disintegrated into
-
1.
Substituting (3.98), (3.99) and (3.100) into (3.96) for and , we obtain
(3.108)
where the index is summed over .
-
2.
Substituting (3.103), (3.104) and (3.105) into (3.101) for and , we obtain
(3.109)
where the index is summed over .
Substituting (3.108) and (3.109) into (3.107), we obtain (3.106). Q.E.D.
Lemma 5 In the case of for and and , the following holds:
where the index is summed over .
Proof In the similar manner as Lemma 4, we obtain (3.110). Q.E.D.
Our triangular double and triple integrals and the divergence theorem of a triangular integral in the 3D space are shown as follows, where D is a domain and ∂D is the boundary of the domain D in the 3D space.
Definition 5 A triangular area double integral in the 3D space is defined as
where the index is summed over .
Definition 6 A triangular triple integral, integrands of which are partial differentials in the 3D space , is defined as
where the indices are summed over .
The following proposition is necessary for the condition (3.118) of Theorem 3.
Proposition 3 Denote constants as , and , then
holds, where the index is summed over .
Proof In the case of , and , Definition 5 is reduced to be
In the case of , and , Definition 5 is reduced to be
In the case of , and , Definition 5 is reduced to be
A linear combination of (3.114), (3.115) and (3.116) is

Q.E.D.
Theorem 3 shown below is the 3D version of Theorem 2, since it derives (3.123) in Corollary 3. The condition (3.118) or (3.121) is the 3D version of the condition (2.17) or (2.39).
Theorem 3 (The divergence theorem of a triangular integral in the 3D space)
Assume D is a domain and ∂D is the boundary of the domain in the -space, expressed in the Cartesian coordinates . Let , and be partially differentiable functions with respect to , and in D. In the case of a closed 2D surface which satisfies
the divergence theorem of a triangular integral in the 3D space holds:

where the indices are summed over and are constants.
Proof Substituting (3.106) and (3.110) into the right-hand side of (3.95), we obtain

where the indices are summed over . Using Proposition 3, (3.118) is rewritten as
where the index is summed over . The limit at infinity of (3.120) under the condition of a closed surface (3.121) is expressed as (3.119) by Definitions 5 and 6. Q.E.D.
Remark The divergence theorem (3.119) shown above is not the conventional one (1.1), which has been familiar to us for two hundred years. The inner product of the nabla and a vector (1.4) is not explicitly shown as an integrand in (3.119).
Corollary 3 shown below derived from Theorem 3 is the 3D version of Corollary 2 derived from Theorem 2. Infinitesimal volume element is introduced as , where the index is summed over .
Corollary 3 (Derivation of the inner product of the nabla and a vector)
In the case of

where is a given function and the index is summed over , the following holds:
Proof Applying Theorem 3 to the left-hand side of (3.122), it is modified to be

where the indices are summed over . In order to hold (3.124) for any value of integral variables, the following four kinds of formulae in two categories are demanded.
-
1.
In the case of ,
 (3.125)
(3.125)

for , where the index is summed over .
-
2.
In the case of ,
 (3.127)
(3.127)

for , where the index is summed over .
Multiplying to the both sides of the four kinds of formulae (3.125), (3.126), (3.127) and (3.128), they are reduced to be the differential equation (3.123). Q.E.D.
Remark We finally obtained the inner product of the nabla and a vector (1.4) by using the antisymmetric symbol, which has explicitly appeared in the conventional divergence theorem (1.1) as the integrand.
Example 2 (A spherical example of the divergence theorem of a triangular integral in the 3D space)
First of all, we see an example which satisfies the condition (3.121) of the divergence theorem (3.118) or (3.121). The condition (3.121) in Theorem 3 is expressed in component representation as

We consider the case of . Using (A.1) and (A.2) or (A.14) and (A.15), we obtain . Thus, the condition (3.129) of the divergence theorem of a triangular integral is reduced to be
Using (A.3) or (A.16), we obtain . In the case of the sphere, (3.130) is satisfied. The details are shown in Appendix C. It is concluded that we are able to apply Theorem 3 for this integrand and the region of the sphere .
Next, the left-hand side of (3.119) is calculated as follows. Calculations in detail are shown in Appendix B in the case of . The each value of the first term of the left-hand side of (3.120) is



The each value of the second term of the left-hand side of (3.120) is



Using (3.111) in Definition 5, the left-hand side of (3.119) is calculated to be

where the index is summed over .
Finally, the right-hand side of (3.119) is calculated as follows. The first term of the right-hand side of (3.120) is reduced to be

where the indices are summed over . The value of each term of the right-hand side of (3.138) is



Substituting (3.139), (3.140) and (3.141) into the right-hand side of (3.138), the value of the first term of the right-hand side of (3.120) is

where the indices are summed over . The second term of the right-hand side of (3.120) is reduced to be

where the indices are summed over . The value of each term of the right-hand side of (3.143) is



Substituting (3.144), (3.145) and (3.146) into the right-hand side of (3.143), the value of the second term of the right-hand side of (3.120) is

where the indices are summed over . Using (3.112) in Definition 6, the sum of (3.142) and (3.147) is the value of the right-hand side of (3.119) as follows:
where the indices are summed over . For the example of the volume of the sphere, the values of both sides of (3.119) are calculated to be (3.137) and (3.148).
4 Integral in the 4D time-space
The quadruple integral is demanded to derive the fundamental equations of the relativistic theories from the variational principle in physics. As the curl theorem of a triangular integral in the 4D time-space was derived in the previous paper [4], the divergence theorem of a triangular integral in the 4D time-space is derived in this paper. In the 3D space, the surface area is divided into parts and each trapezium is divided into triangles. In the 4D time-space, the hyper-surface area is divided into parts and each hyper-trapezium is divided into tetrahedra.
Let be a piecewise smooth hyper-surface of the equation in the -time-space, expressed in the Cartesian coordinates . Suppose there are kinds of triple sequences of points , , , , and for and and on . In the previous section, kinds of finite area element vectors and in the 3D space are respectively introduced as (3.1) and (3.4). In this section, we introduce kinds of finite hyper-surface element vectors , , , , and in the 4D time-space.
4.1 Six kinds of finite hyper-surface element vectors in the 4D time-space
In the following, the Cartesian coordinates are denoted as , , and . Before expressing the following formulae in tensor representation, the antisymmetric symbol in the 4D time-space is introduced as
In the 4D time-space, holds for , where the indices are summed over .
-
1.
The first finite hyper-surface element vector for and and and is disintegrated into three parts,
(4.2)
where , , and are respectively μ-components of , , and . Here, , and for and and and are respectively inferred as



where the indices are summed over .
-
(a)
Introducing
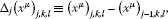 (4.6)
(4.6)


for and and and , we may modify each factor of (4.3) as follows:



Substituting (4.9), (4.10) and (4.11) in (4.3) for and and and , we may modify it as
where the indices are summed over .
-
(b)
In the similar manner, (4.4) for and and and is modified to be
(4.13)
where the indices are summed over .
-
(c)
In the similar manner, (4.5) for and and and is modified to be
(4.14)
where the indices are summed over .
Substituting (4.12), (4.13) and (4.14) into (4.2) for and and and , we may modify it as
where the indices are summed over .
In the similar manner, we calculate the case of , , , and as follows.
-
2.
The second finite hyper-surface element vector for and and and is
(4.16)
where the indices are summed over .
-
3.
The third finite hyper-surface element vector for and and and is
(4.17)
where the indices are summed over .
-
4.
The fourth finite hyper-surface element vector for and and and is
(4.18)
where the indices are summed over .
-
5.
The fifth finite hyper-surface element vector for and and and is
(4.19)
where the indices are summed over .
-
6.
The sixth finite hyper-surface element vector for and and and is
(4.20)
where the indices are summed over .
Proposition 4 The volume V of the 3D hyper-surface of the 4D hyper-body in is expressed as
under the condition of
where , , , , and are the finite hyper-surface elements and , , , , and are corresponding unit normal vectors of respective finite hyper-surface elements.
4.2 The divergence theorem of a triangular integral in the 4D time-space
In the following subsection, we prepare definitions and notations for extending Theorem 3 and Corollary 3 in the 4D time-space. Assume there are four functions , , and of the four variables t, x, y and z in the Cartesian coordinates of the 4D time-space. Suppose there are sets of triple dependent sequences (4.23), (4.24), (4.25), (4.26), (4.27) and (4.28) as follows. Denoting , , and , the kinds of integrand vectors , , , , and for and and and are expressed as






Replacing a normal vector in the 4D time-space by a general vector in the 4D time-space, where , we introduce the following triple dependent sums:

where the index is summed over . In order to prove Theorem 4, , , , , and are respectively modified in Lemmata 6, 7, 8, 9, 10 and 11.
-
1.
The total increments of for and are denoted as
(4.30)
The increments of for and are denoted as
The partial increments of for and are denoted as




-
2.
The total increments of for and are denoted as
(4.36)
The increments of for and are denoted as
The partial increments of for and are denoted as




-
3.
The total increments of for and and are denoted as
(4.42)
The increments of for and and are denoted as
The partial increments of for and and are denoted as




Lemma 6 In the case of for and and and , the following holds:
where the index is summed over .
Proof Using (4.30), (4.36) and (4.42), for and and and is disintegrated into
-
1.
Substituting (4.32), (4.33), (4.34) and (4.35) into (4.30) for and , we obtain
(4.50)
where the index is summed over .
-
2.
Substituting (4.38), (4.39), (4.40) and (4.41) into (4.36) for and , we obtain
(4.51)
where the index is summed over .
-
3.
Substituting (4.44), (4.45), (4.46) and (4.47) into (4.42) for and and , we obtain
(4.52)
where the index is summed over .
Substituting (4.50), (4.51) and (4.52) into (4.49), we obtain (4.48). Q.E.D.
In the similar manner, we obtain the cases of , , , and as follows.
Lemma 7 In the case of for and and and , the following holds
where the index is summed over .
Lemma 8 In the case of for and and and , the following holds:
where the index is summed over .
Lemma 9 In the case of for and and and , the following holds:
where the index is summed over .
Lemma 10 In the case of for and and and , the following holds:
where the index is summed over .
Lemma 11 In the case of for and and and , the following holds:
where the index is summed over .
Our triangular triple and quadruple integrals and the divergence theorem of a triangular integral in the 4D time-space are shown as follows, where D is a domain and ∂D is the boundary of the domain in the 4D time-space.
Definition 7 A triangular hyper-surface triple integral in the 4D time-space is defined as

where the index is summed over .
Definition 8 A triangular quadruple integral, integrands of which are partial differentials in the 4D time-space  , is defined as
, is defined as

where the indices are summed over .
Proposition 5 Denote constants as , , and , then
holds, where the index is summed over .
Proof In the case of , , and , Definition 7 is reduced to be
In the case of , , and , Definition 7 is reduced to be
In the case of , , and , Definition 7 is reduced to be
In the case of , , and , Definition 7 is reduced to be
A linear combination of (4.61), (4.62), (4.63) and (4.64) is

Q.E.D.
Theorem 4 shown below is the 4D version of Theorems 2 and 3. The condition (4.66) or (4.69) is the 4D version of the condition (2.17) or (2.39) on the 2D plane and the condition (3.118) or (3.121) in the 3D space.
Theorem 4 (The divergence theorem of a triangular integral in the 4D time-space)
Assume D is a domain and ∂D is the boundary of the domain in the -time-space, expressed in the Cartesian coordinates . Let , , and be partially differentiable functions with respect to , , and in D. In the case of a closed 3D hyper-surface which satisfies
the divergence theorem of a triangular integral in the 4D time-space holds:

where the indices are summed over and are constants.
Proof Substituting (4.48), (4.53), (4.54), (4.55), (4.56) and (4.57) into the right-hand side of (4.29), we obtain

where the indices are summed over . Using Proposition 5, (4.66) is rewritten as

where the index is summed over . The limit at infinity of (4.68) under the condition of (4.69) is expressed as (4.67) by Definitions 7 and 8. Q.E.D.
Corollary 4 shown below is the 4D version of Corollary 3. We only consider the case of for simplicity.
Corollary 4 In the case of

where the index is summed over , the following holds:
Proof Applying Theorem 4 to the left-hand side of (4.70), it is modified to be

where the indices are summed over . In order to hold (4.72) for any value of integral variables, the following fifteen kinds of formulae in three categories are demanded.
-
1.
In the case of ,
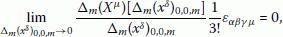 (4.73)
(4.73)


for , where the index is summed over .
-
2.
In the case of ,
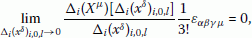 (4.76)
(4.76)





for , where the index is summed over .
-
3.
In the case of and ,
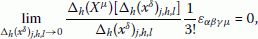 (4.82)
(4.82)





for , where the index is summed over .
Multiplying to the both sides of the fifteen kinds of formulae (4.73), (4.74), (4.75), (4.76), (4.77), (4.78), (4.79), (4.80), (4.81), (4.82), (4.83), (4.84), (4.85), (4.86) and (4.87), they are reduced to be the differential equation (4.71). Q.E.D.
5 Conclusion
The conventional multiple rectangular integral is merely the inverse operation of the partial differential. It is impossible to regard the conventional multiple rectangular integral as the inverse operation of the total differential in the derivation of the conventional curl or divergence theorem. There should be the inverse operation of the total differential in this sense. Fortunately, both of the curl and the divergence theorems are derived by substituting the total differentials into our new method of a triangular integral. We thus infer that our new method of a triangular integral must be the inverse operation of the total differential.
Appendix A: The concrete forms of increments of the sphere
-
1.
The upper-right finite area element vector .
Substituting (3.73) and (3.74) into (3.41), (3.42) and (3.43), we respectively obtain



for and .
-
(a)
The concrete forms of , and in the case of the sphere.
Applying (A.1), (A.2) and (A.3) to (3.44), (3.45) and (3.46), respectively, we obtain



for and .
-
(b)
The concrete forms of , and in the case of the sphere.
Applying (A.1) and (A.2) to (3.47) and (3.48), respectively, we obtain


for and .
-
(c)
The concrete forms of , and in the case of the sphere.
Applying (A.1), (A.2) and (A.3) to (3.50), (3.51) and (3.52), respectively, we obtain


for and .
-
(d)
The concrete forms of , and in the case of the sphere.
Applying (A.1), (A.2) and (A.3) to (3.53), (3.54) and (3.55), respectively, we obtain



for and .
-
2.
The lower-left finite area element vector .
Substituting (3.76) and (3.77) into (3.58), (3.59) and (3.60), we respectively obtain



for and .
-
(a)
The concrete forms of , and in the case of the sphere.
Applying (A.14), (A.15) and (A.16) to (3.61), (3.62) and (3.63), respectively, we obtain



for and .
-
(b)
The concrete forms of , and in the case of the sphere.
Applying (A.14) and (A.15) to (3.64) and (3.65), respectively, we obtain


for and .
-
(c)
The concrete forms of , and in the case of the sphere.
Applying (A.14) and (A.15) to (3.67) and (3.68), respectively, we obtain


for and .
-
(d)
The concrete forms of , and in the case of the sphere.
Applying (A.14), (A.15) and (A.16) to (3.70), (3.71) and (3.72), respectively, we obtain



for and .
Appendix B: The surface area and the volume of the sphere
-
1.
The upper-right finite area element vector .
-
(a)
In the case of a double increment .
Substituting (A.8), (3.49) and (A.6) into (3.10), the value of is

Substituting (A.7), (3.49) and (A.6) into (3.11), the value of is

Substituting (A.7), (A.8), (A.4) and (A.5) into (3.12), the value of
is

-
(b)
In the case of a double increment .
Substituting (A.12), (A.13), (A.10) and (3.52) into (3.16), the value of
is

Substituting (A.11), (A.13), (A.9) and (3.52) into (3.17), the value of
is

Substituting (A.11), (A.12), (A.9) and (A.10) into (3.18), the value of
is

-
2.
The lower-left finite area element vector .
-
(a)
In the case of a double increment .
Substituting (A.21), (3.66), (A.18) and (A.19) into (3.21), the value of
is

Substituting (A.20), (3.66), (A.17) and (A.19) into (3.22), the value of
is

Substituting (A.20), (A.21), (A.17) and (A.18) into (3.23), the value of
is

-
(b)
In the case of a double increment .
Substituting (A.25), (A.26), (A.23) and (3.69) into (3.26), the value of
is

Substituting (A.24), (A.26), (A.22) and (3.69) into (3.27), the value of
is

Substituting (A.24), (A.25), (A.22) and (A.23) into (3.28), the value of
is

Appendix C: The condition of the closed surface of the sphere
In the case of the sphere, the calculations of (3.130) in detail are shown as follows:


References
Lebesgue H: Intégrale, longueur, aire. Ann. Mat. Pura Appl. 1902, 7(3):231–359. Thèses présentées à la Faculté des sciences de Paris pour obtenir le grade de Docteur ès sciences mathématiques. Bernardoni de C. Rebeschini, Milano (1902)
Lebesgue H: Leçon sur L’intégration et la Recherche des Fonctions Primitives. Gauthier-Villars, Paris; 1904.
Cartan É: Sur l’intégration des systèmes d’équations aux différentielles totales. Ann. Sci. Éc. Norm. Super. 1901, 18(3):241–311.
Tokunaga K: The curl theorem of a triangular integral. Adv. Differ. Equ. 2012., 2012: Article ID 23. doi:10.1186/1687–1847–2012–23
Bramble JH, Zlámal M: Triangular elements in the finite element method. Math. Comput. 1970, 24(112):809–820. 10.1090/S0025-5718-1970-0282540-0
Acknowledgements
The author thanks Professor Susumu Ishikawa at Fukuoka Institute of Technology for refining this theory.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that he has no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tokunaga, K. The divergence theorem of a triangular integral. Adv Differ Equ 2012, 168 (2012). https://doi.org/10.1186/1687-1847-2012-168
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-168

 </p><p> for and .
</p><p> for and .

 </p><p> for and .
</p><p> for and .