- Research
- Open access
- Published:
On -equivalence of impulsive differential equations and its applications to partial impulsive differential equations
Advances in Difference Equations volume 2012, Article number: 144 (2012)
Abstract
By means of the Schauder-Tychonoff principle, -equivalence are established between linear and nonlinear perturbed impulsive differential equations with an unbounded linear part in an arbitrary Banach space. The feasibility of our theoretical results is illustrated by an example involving partial impulsive differential equations of the parabolic type.
MSC:34A37, 35Q72, 47H10.
1 Introduction
Theory of impulsive differential equations has been emerging as an important area of investigation since these equations provide natural frameworks for describing many real life phenomena appearing in physics, chemical technology, population dynamics, and economics; see the remarkable monographs [1–3]. There have been significant contributions regarding the investigations of qualitative properties of solutions of such equations in the last three decades [4–12]. However, dealing with nonlinear impulsive differential equations have faced, as usual, several drawbacks that caused slackening progress of this theory.
One of the most important ways to investigate the asymptotic structure of two equations is to build asymptotic equivalence between their solutions. Establishing such equivalence enables researchers to comment on the asymptotic behavior of solutions of certain nonlinear equations by studying another linear equation whose solutions bear the same character. In spite of the fact that this way is of great significance in the theory of analysis, it has been less considered in the literature.
In this paper, we introduce the definition of -equivalence between linear and nonlinear perturbed impulsive differential equations with an unbounded linear part in an arbitrary Banach space. By means of the Schauder-Tychonoff principle, sufficient conditions are established to guarantee the existence of such equivalence. To expose the feasibility of our theoretical results, an example involving partial impulsive differential equations of the parabolic type is provided. Similar problems but with different approaches regarding -equivalence for impulsive differential equations were first reported in the papers [13–17].
2 Statement of the problem
Let be a Banach space with the norm and the identical operator I. By , we will denote the domain of the operator .
Consider the following two impulsive differential equations:
and
where (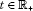 ) and are linear and possibly unbounded operators. The functions
) and are linear and possibly unbounded operators. The functions  and are continuous where . The sets and are dense in . The points of jumps satisfy the conditions with . We set and ().
and are continuous where . The sets and are dense in . The points of jumps satisfy the conditions with . We set and ().
Furthermore, we assume that all functions under consideration are left continuous and that there exists the Cauchy operator () of the linear equation
Sufficient conditions for the existence of can be found in [18, 19]. One can easily check that
is the Cauchy operator of the linear impulsive differential equation (1). We observe that the operator is bounded if one of the following conditions hold:
(B1) are bounded operators, .
(B2) are bounded operators, .
Lemma 1 Let one of the conditions (B 1) or (B 2) hold. Then the solution of the equation
satisfies the impulsive differential equation (2).
The proof of the above statement is straightforward and can be achieved by direct substitution.
Let the following condition be fulfilled:
(H) There exists continuous function  such that
such that
where and .
We introduce the following spaces:

and

with the norms

The following conditions are needed in the sequel:
(H1) There exists constant such that  .
.
(H2) There exists constant such that  .
.
Definition 1 Equation (2) is called -equivalent to Eq. (1) in the nonempty, closed, and convex subset B of if there exists a convex and closed subset D of such that for any solution of (1) lying in the set B there exists a solution of (2) lying in the set , and satisfying the relation .
If Eq. (2) is -equivalent to Eq. (1) in the set B, and vice versa, we say that Eqs. (1) and (2) are -equivalent in the set B.
By  , we denote the linear set of all functions which are continuous for (), having left and right limits at points and are left continuous. The set
, we denote the linear set of all functions which are continuous for (), having left and right limits at points and are left continuous. The set  is a locally convex space with respect to the metric
is a locally convex space with respect to the metric
The convergence with respect to this metric coincides with the uniform convergence on each bounded interval. For this space, an analogue of Arzella-Ascoli’s theorem is valid.
Lemma 2 ([13])
The set  is relatively compact if the intersections are relatively compact for
is relatively compact if the intersections are relatively compact for  and M is equicontinuous on each interval , .
and M is equicontinuous on each interval , .
The proof of the above theorems is completed by applying the theorem of Arzella-Ascoli on each interval , and constitutes a diagonal line sequence.
Let C be a nonempty subset of X. Set

We now have the following lemma.
Lemma 3 ([17])
Let C be a nonempty, convex, and closed subset of . Suppose an operator T transforms into itself and is continuous and compact. Then T has a fixed point in .
The proof of Lemma 3 follows by utilizing the fixed-point principle of Schauder-Tychonoff.
The following lemmas are borrowed from [14].
Lemma 4 ([14])
Let the following conditions be fulfilled:
-
1.
Condition (B 1) (or (B 2)) holds.
-
2.
Conditions (H), (H 1), and (H 2) hold.
Then, for any function and for any sequence , the linear nonhomogeneous impulsive differential equation
has a bounded solution for which
and
Lemma 5 ([14])
Let the following conditions be fulfilled:
-
1.
Condition (B 1) (or (B 2)) holds.
-
2.
Conditions (H) and (H 1) hold.
Then the operator defined by the formula
maps into and the following estimate is valid:
where .
Lemma 6 ([14])
Let the following conditions be fulfilled:
-
1.
Condition (B 1) (or (B 2)) holds.
-
2.
Conditions (H) and (H 2) hold.
Then the operator , defined by the formula
maps into and the following estimate is valid:
where .
3 The main results
Set
where is the solution of Eq. (1) and is the solution of Eq. (2).
Then and is solution of the linear nonhomogeneous impulsive differential equation (6) for and . Consequently,
We define the operator
Theorem 1 Let the following conditions be fulfilled:
-
1.
Condition (B 1) (or (B 2)) holds.
-
2.
Conditions (H), (H 1), and (H 2) hold.
-
3.
There exists a nonempty, convex, and closed subset D of X such that

-
4.
For any fixed , the following inclusions hold:
4.1 (),
4.2 (), where is for any fixed 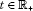 and is for any fixed a compact subset of X.
and is for any fixed a compact subset of X.
-
5.
, for
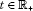 , where the function is continuous and .
, where the function is continuous and . -
6.
, for , where the sequence .
Then Eq. (2) is -equivalent to Eq. (1) in the set B and the following estimate is valid:
Proof We will prove that for each solution of Eq. (1) lying in the set B the operator has a fixed point such that and lies in .
In view of condition 3 of Theorem 1, it follows that the operator defined by (13) maps the set

into itself for .
Let  . We will show the equicontinuity of the functions in the set M. Let and . It can be verified that
. We will show the equicontinuity of the functions in the set M. Let and . It can be verified that
The continuity of the function on , condition (H) and condition 5 of Theorem 1 imply the equicontinuity of the set M.
From condition 4 of Theorem 1 and (13), we deduce the compactness of the intersections for 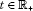 . Consequently, from Lemma 2, it follows that the set M is compact.
. Consequently, from Lemma 2, it follows that the set M is compact.
We will show that the operator is continuous in  . Let the sequence be convergent to the function in the metric of the space
. Let the sequence be convergent to the function in the metric of the space  .
.
Then the sequence
tends to for any 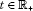 and the sequence
and the sequence
tends to coordinate-wisely ().
From conditions 5 and 6 of Theorem 1, it follows that

and
In virtue of the theorem of Lebesgue, we take the limit inside the integral and obtain that the sequence of functions tends for 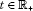 to the function . On the other hand, by the analogue of the theorem of Lebesgue for the series, we obtain that the sequence of functions tends to the function . Since the functions
to the function . On the other hand, by the analogue of the theorem of Lebesgue for the series, we obtain that the sequence of functions tends to the function . Since the functions
lie in a compact set, they also tend to the metric of the space  .
.
In view of Lemma 3, it follows that for any the operator has a fixed point , that is, .
From conditions 5 and 6 of Theorem 1, Lemma 5, and Lemma 6, it follows that this fixed point and the following estimate is valid:
where . □
Remark 1 The case when the operator (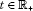 ) is linear bounded and the sets B and D are balls is considered in [15].
) is linear bounded and the sets B and D are balls is considered in [15].
We shall illustrate the effectiveness of Theorem 1 by constructing an example involving the partial impulsive differential equations. For more details on the general theory of partial impulsive differential equations, we suggest that the reader consults [20, 21].
4 An example
In this section, we consider linear and nonlinear perturbed partial impulsive differential equations. We transform these equations to ordinary impulsive differential equations with an unbounded linear operator and show that they satisfy the conditions of Theorem 1. More information regarding the theory of ordinary differential equations with an unbounded linear operator can be reached at [19].
Let Ω be a bounded domain with smooth boundary ∂ Ω in  , , and .
, , and .
We denote
and
Consider the following linear impulsive parabolic initial value problem:
and the nonlinear perturbed impulsive parabolic initial value problem
where , () are linear operators and  and
and  are continuous functions.
are continuous functions.
Let  (), where
(), where

with the norm .
Along with the family , 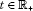 of strongly elliptic operators, we associate a family of linear operators ,
of strongly elliptic operators, we associate a family of linear operators , 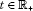 acting in X by
acting in X by
This is can be achieved as follows: , 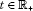 .
.
Let (). We set

and

where , lie dense in X and are linear operators,  and are continuous functions.
and are continuous functions.
We claim that Eqs. (1) and (2) are -equivalent. Let be the Cauchy operator of the linear equation (3).
Sufficient conditions for the validity of the estimate
can be found in [19].
Let (), , and ( ), where the positive constants α, γ, and satisfy , and . The functions
), where the positive constants α, γ, and satisfy , and . The functions  () are defined such that for each
() are defined such that for each 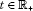 .
.
Then

and
We shall find the function () of condition (H). Let and . Then the following estimate is valid
Set
For the constant of condition (H1), we obtain

Hence,
For the constant of condition (H2), we obtain

Hence,
Let and
We shall find the function and the sequence so that conditions 5 and 6 of Theorem 1 are satisfied. We observe that
and
Hence, and .
It remains to show that and . Indeed

and

Set . We shall show that for any (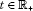 ), the operator defined by (13) maps the set
), the operator defined by (13) maps the set

into itself.
From (8), (13), and (16), we obtain
for each 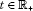 . Hence, the operator maps the set into itself.
. Hence, the operator maps the set into itself.
By means of a compactness criterion in [22], we shall prove condition 4.1. We observe that the set
is compact subset of X for any fixed 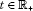 . Indeed
. Indeed
and
and hence , where N is a positive constant.
We shall show that
This follows from the relations below
In a similar way, one can show the validity of condition 4.2. The conditions of Theorem 1 are fulfilled, and hence Eqs. (1) and (2) are in -equivalent. Hence, every solution of (14) induces a solution of (15) such that the function lies in for any .
References
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. World Scientific, Singapore; 1989.
Bainov DD, Covachev V: Impulsive Differential Equations with a Small Parameter. World Scientific, Singapore; 1994.
Samoilenko AM, Perestyuk NA: Differential Equations with Impulse Effect. World Scientific, Singapore; 1995.
Ahmad S, Stamov G: On the almost periodic processes in impulsive competitive systems with delay and impulsive perturbations. Nonlinear Anal., Real World Appl. 2009, 10(5):2857–2863. 10.1016/j.nonrwa.2008.09.003
Ahmad S, Stamov GT: Almost periodic solutions of n -dimensional impulsive competitive systems. Nonlinear Anal., Real World Appl. 2009, 10(3):1846–1853. 10.1016/j.nonrwa.2008.02.020
Akhmet MU, Alzabut JO, Zafer A: Perron’s theorem for linear impulsive differential equations with distributed delay. J. Comput. Appl. Math. 2006, 193(1):204–218. 10.1016/j.cam.2005.06.004
Allegretto W, Papini D, Forti M: Common asymptotic behavior of solutions and almost periodicity for discontinuous delayed and impulsive networks. IEEE Trans. Neural Netw. 2010, 21(7):1110–1125.
Alzabut JO, Nieto JJ, Stamov GT: Existence and exponential stability of positive almost periodic solutions for a model of hematopoiesis. Bound. Value Probl. 2009., 2009: Article ID 127510
Bin L, Xinzhi L, Xiaoxin L: Robust stability of uncertain dynamical systems. J. Math. Anal. Appl. 2004, 290(2):519–533. 10.1016/j.jmaa.2003.10.035
Alwan MS, Liu X, Xie W: Existence, continuation, and uniqueness problems of stochastic impulsive systems with time delay. J. Franklin Inst. 2010, 347(7):1317–1333. 10.1016/j.jfranklin.2010.06.005
Zou L, Xiong Z, Shu Z: The dynamics of an eco-epidemic model with distributed time delay and impulsive control strategy. J. Franklin Inst. 2011, 348(9):2332–2349. 10.1016/j.jfranklin.2011.06.023
Li X, Rakkiyappan R, Balasubramaniam P: Existence and global stability analysis of equilibrium of fuzzy cellular neural networks with time delay in the leakage term under impulsive perturbations. J. Franklin Inst. 2011, 348(2):135–155. 10.1016/j.jfranklin.2010.10.009
Bainov DD, Kostadinov S, Zabreiko P:-equivalence of impulsive equations. Int. J. Theor. Phys. 1988, 27(11):1411–1424. 10.1007/BF00671319
Georgieva A:Properties of -solutions of linear nonhomogeneous impulsive differential equations with unbounded linear operator. Anniversary International Conference REMIA 2010, 129–135.
Georgieva A, Kostadinov S:-equivalence between a linear and a nonlinear perturbed impulse differential equations with bounded linear part. J. Tech. Univ. Plovdiv, Fundam. Sci. Appl., Ser. A, Pure Appl. Math. 2007, 12: 33–42.
Georgieva A, Kostadinov S:-equivalence between two nonlinear impulse differential equations with unbounded linear parts and its application for partial impulse differential equations. Rostock. Math. Kolloqu. 2009, 64: 55–66.
Georgieva A, Kostadinov S:Sufficient conditions for the -equivalence between two nonlinear impulse differential equations. Turk. J. Math. 2008, 32: 451–466.
Krasnoselski, M, Zabreiko, P, Pustilnic, E, Sobolevski, P: Integrable Operators in Spaces of Integrable Functions. Moscow (1966) (in Russian)
Pazy A: Semigroups of Linear Operators. Springer, Berlin; 1983.
Erbe L, Freedman H, Liu X, Wu J: Comparison principle for impulsive parabolic equations with applications to models of single species growth. J. Aust. Math. Soc. Ser. B 1991, 32: 382–400. 10.1017/S033427000000850X
Xiao J, Nieto JJ: Variational approach to some damped Dirichlet nonlinear impulsive differential equations. J. Franklin Inst. 2011, 348(2):369–377. 10.1016/j.jfranklin.2010.12.003
Maurin K: Metody Przestrzeni Hilberta. Panstwowe Wydawnictwo Naukove, Warsaw; 1959. in Russian
Acknowledgements
The authors would like to express their sincere thanks to the editor, Professor Dr. Sandra Pinelas, for handling our paper during the reviewing process and to the referees for suggesting some corrections that helped make the contents of the paper more accurate.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have achieved equal contributions to each part of this paper. All authors read and approved the final version of the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Georgieva, A., Kostadinov, S., Stamov, G. et al. On -equivalence of impulsive differential equations and its applications to partial impulsive differential equations. Adv Differ Equ 2012, 144 (2012). https://doi.org/10.1186/1687-1847-2012-144
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-144
