- Research
- Open access
- Published:
Existence and globally exponential stability of equilibrium for fuzzy BAM neural networks with distributed delays and impulse
Advances in Difference Equations volume 2011, Article number: 8 (2011)
Abstract
In this article, fuzzy bi-directional associative memory neural networks with distributed delays and impulses are considered. Some sufficient conditions for the existence and globally exponential stability of unique equilibrium point are established using fixed point theorem and differential inequality techniques. The results obtained are easily checked to guarantee the existence, uniqueness, and globally exponential stability of equilibrium point.
MSC: 34K20; 34K13; 92B20
Introduction
The bidirectional associative memory neural networks (BAM) models were first introduced by Kosko [1, 2]. It is a special class of recurrent neural networks that can store bipolar vector pairs. The BAM neural network is composed of neurons arranged in two layers, the X-layer and Y-layer. The neurons in one layer are fully interconnected to the neurons in the other layer, while there are no interconnections among neurons in the same layer. Through iterations of forward and backward information flows between the two layers, it performs two-way associative search for stored bipolar vector pairs and generalize the single-layer autoassociative Hebbian correlation to two-layer pattern-matched heteroassociative circuits. Therefore, this class of networks possesses a good applications prospects in the areas of pattern recognition, signal and image process, automatic control. Recently, they have been the object of intensive analysis by numerous authors. In particular, many researchers have studied the dynamics of BAM neural networks with or without delays [1–23] including stability and periodic solutions. In Refs. [1–9], the authors discussed the problem of the stability of the BAM neural networks with or without delays, and obtained some sufficient conditions to ensure the stability of equilibrium point. Recently, some authors, see [10], [14, 15] investigated another dynamical behaviors-periodic oscillatory, some sufficient conditions are obtained to ensure other solution converging the periodic solution. In this article, we would like to integrate fuzzy operations into BAM neural networks and maintain local connectedness among cells. Speaking of fuzzy operations, Yang et al. [24–26] first combined those operations with cellular neural networks and investigated the stability of fuzzy cellular neural networks (FCNNs). Studies have shown that FCNNs has its potential in image processing and pattern recognition, and some results have been reported on stability and periodicity of FCNNs [24–30]. On the other hand, time delays inevitably occurs in electronic neural networks owing to the unavoidable finite switching speed of amplifiers. It is desirable to study the fuzzy BAM neural networks which has a potential significance in the design and applications of stable neural circuits for neural networks with delays.
Though the non-impulsive systems have been well studied in theory and in practice (e.g., see [1–3, 5–30] and references cited therein), the theory of impulsive differential equations is now being recognized to be not only richer than the corresponding theory of differential equations without impulse, but also represents a more natural framework for mathematical modelling of many real-world phenomena, such as population dynamic and the neural networks. In recent years, the impulsive differential equations have been extensively studied (see the monographs and the works [4, 31–35]). Up to now, to the best of our knowledge, dynamical behaviors of fuzzy BAM neural networks with delays and impulses are seldom considered. Motivated by the above discussion, in this article, we investigate the fuzzy BAM neural networks with distributed delays and impulses by the following system

where n and m correspond to the number of neurons in X-layer and Y -layer, respectively. x
i
(t) and y
j
(t) are the activations of the i th neuron and the j th neurons, respectively, a
i
> 0, b
j
> 0 denote the rate with which the i th neuron and j th neuron will reset its potential to the resting state in isolation when disconnected from the network and external inputs; α
ji
, β
ji
, T
ji
, and H
ji
are elements of fuzzy feedback MIN template and fuzzy feedback MAX template, fuzzy feed-forward MIN template, and fuzzy feed-forward MAX template in X-layer, respectively; p
ij
, q
ij
, K
ij
, and L
ij
are elements of fuzzy feedback MIN template and fuzzy feedback MAX template, fuzzy feed-forward MIN template, and fuzzy feed-forward MAX template in Y -layer, respectively; ∧ and ∨ denote the fuzzy AND and fuzzy OR operation, respectively; u
j
and u
i
denote external input of the i th neurons in X-layer and external input of the j th neurons in Y -layer, respectively; A
i
and B
j
represent bias of the i th neurons in X-layer and bias of the j th neurons in Y -layer,respectively; c
ji
(t) and d
ij
(t) are the delayed feedback.  are the impulses at moments t
k
and t
1 < t
2 < ⋯ is a strictly increasing sequences such that lim
k→ ∞
t
k
= +∞. τ > 0 and σ > 0 are constants and correspond to the transmission delays, and f
j
(·), g
i
(·) are signal transmission functions.
are the impulses at moments t
k
and t
1 < t
2 < ⋯ is a strictly increasing sequences such that lim
k→ ∞
t
k
= +∞. τ > 0 and σ > 0 are constants and correspond to the transmission delays, and f
j
(·), g
i
(·) are signal transmission functions.
The main purpose of this article is, employing fixed point theorem and differential inequality techniques, to give some sufficient conditions for the existence, uniqueness, and global exponential stability of equilibrium point of system (1). Our results extend and improve the corresponding works in the earlier publications.
The initial conditions associated with system (1) are of the form

where ϕ i (·) and ψ j (·) are continuous bounded functions defined on [-σ, 0] and [-τ; 0], respectively.
Throughout this article, we always make the following assumptions.
(A1) The signal transmission functions f j (·), g i (·)(i = 1, 2, ..., n, j = 1, 2, ..., m) are Lipschitz continuous on R with Lipschitz constants μ j and ν i , namely, for x, y ∈ R

(A2) For i = 1,2, ..., n, j = 1,2, ..., m, there exist nonnegative constants  such that
such that


As usual in the theory of impulsive differential equations, at the points of discontinuity t
k
of the solution t α (x
1(t), ..., x
n
(t), y
1
(t), ..., y
m
(t))T. We assume that (x
1(t), ..., x
n
(t), y
1(t), ..., y
m
(t))T = (x
1(t - 0), ..., x
n
(t - 0), y
1(t - 0), ..., y
m
(t - 0))T . It is clear that, in general, the derivatives  and
and  do not exist. On the other hand, according to system (1), there exist the limits
do not exist. On the other hand, according to system (1), there exist the limits  and
and  . In view of the above convention, we assume that
. In view of the above convention, we assume that  and
and  .
.
To be convenience, we introduce some notations. x = (x 1, x 2, ..., x l )T ∈ R l denotes a column vector, in which the symbol (T) denotes the transpose of vector. For matrix D = (d ij ) l×l , D T denotes the transpose of D, and E l denotes the identity matrix of size l. A matrix or vector D ≥ 0 means that all entries of D are greater than or equal to zero. D > 0 can be defined similarly. For matrices or vectors D and E, D ≥ E (respectively D > E) means that D - E ≥ 0 (respectively D - E > 0). Let us define that for any ω ∈ R n+m, ||ω|| = max1≤k≤n+m |ω k |.
Definition 1.1. Let  be an equilibrium point of system (1) with
be an equilibrium point of system (1) with  . If there exist positive constants M, λ such that for any solution z(t) = (x
1(t), x
2(t), ..., x
n
(t), y
1(t), y
2(t), ..., y
m
(t))T of system (1) with initial value (ϕ,ψ) and ϕ = (ϕ
1(t), ϕ
2(t), ..., ϕ
n
(t))T ∈ C([-σ, 0], R
n ), ψ = (ψ
1(t), ψ
2(t), ..., ψ
m
(t))T ∈ C([-τ, 0], R
m ),
. If there exist positive constants M, λ such that for any solution z(t) = (x
1(t), x
2(t), ..., x
n
(t), y
1(t), y
2(t), ..., y
m
(t))T of system (1) with initial value (ϕ,ψ) and ϕ = (ϕ
1(t), ϕ
2(t), ..., ϕ
n
(t))T ∈ C([-σ, 0], R
n ), ψ = (ψ
1(t), ψ
2(t), ..., ψ
m
(t))T ∈ C([-τ, 0], R
m ),

where i = 1, 2, ..., n, j = 1, 2, ..., m

Then z* is said to be globally exponentially stable.
Definition 1.2. If f(t): R → R is a continuous function, then the upper left derivative of f(t) is defined as

Definition 1.3 . A real matrix A = (a ij ) l × l is said to be an M-matrix if a ij ≤ 0, i, j = 1,2, ..., l, i ≠ j, and all successive principal minors of A are positive.
Lemma 1.1. Let A = (a ij ) be an l × l matrix with non-positive off-diagonal elements. Then the
following statements are equivalent:
-
(i)
A is an M-matrix;
-
(ii)
the real parts of all eigenvalues of A are positive;
-
(iii)
there exists a vector η > 0 such that Aη > 0;
-
(iv)
there exists a vector ξ > 0 such that ξ T A > 0;
-
(v)
there exists a positive definite l × l diagonal matrix D such that AD + DA T > 0.
Lemma 1.2[24]. Suppose × and y are two states of system (1), then we have

and

Lemma 1.3 Let A ≥ 0 be an l × l matrix and ρ(A) < 1, then (E l - A)-1 ≥ 0, where ρ(A) denotes the spectral radius of A.
The remainder of this article is organized as follows. In next section, we shall give some sufficient conditions for checking the existence and uniqueness of equilibrium point, followed by some sufficient conditions for global exponential stability of the unique equilibrium point of (1). Then, an example will be given to illustrate effectiveness of our results obtained. Finally, general conclusion is drawn.
Existence and uniqueness of equilibrium point
In this section, we will derive some sufficient conditions for the existence and uniqueness of equilibrium point for fuzzy BAM neural networks model (1).
Theorem 2.1. Suppose that (A1) and (A2) hold and ρ(D -1 EU) < 1, where D = diag(a 1, ..., a n , b 1, ..., b m ), U = diag(μ 1, ..., μ n , ν 1, ..., ν m )

Then there exists a unique equilibrium point of system (1).
Proof. An equilibrium point  is a constant vector satisfying system (1), i.e.,
is a constant vector satisfying system (1), i.e.,

To finish the proof, it suffices to prove that (5) has a unique solution. Consider a mapping Φ = (Φ i , Ψ j )T : R n+m→ R n+mdefined by


We show that Φ: R
n+m→ R
n+mis global contraction mapping on R
n+m. In fact, for h = (h
1, h
2, ..., h
n
, v
1, v
2, ..., v
m
)T,  . Using (A1), (A2), and Lemma 1.2, we have
. Using (A1), (A2), and Lemma 1.2, we have


In view of (8)-(9), it follows that

where F = D -1 EU = (w ij )(n+m) × (n+m). Let ξ be a positive integer. Then from (10) it follows that

Since ρ(F) < 1, we obtain lim ξ→+∞ F ξ = 0, which implies that there exist a positive integer N and a positive constant r < 1 such that

Nothing that (11) and (12), it follows that

which implies that  . Since r < 1, it is obvious that the mapping Φ N : R
n+m→ R
n+mis a contraction mapping. By the fixed point theorem of Banach space, Φ possesses a unique fixed point in R
n+mwhich is unique solution of the system (5), namely, there exist a unique equilibrium point of system (1). The proof of theorem 2.1 is completed.
. Since r < 1, it is obvious that the mapping Φ N : R
n+m→ R
n+mis a contraction mapping. By the fixed point theorem of Banach space, Φ possesses a unique fixed point in R
n+mwhich is unique solution of the system (5), namely, there exist a unique equilibrium point of system (1). The proof of theorem 2.1 is completed.
Global exponential stability of equilibrium point
In this section, we shall give some sufficient conditions to guarantee global exponential stability of equilibrium point of system (1).
Theorem 3.1 Suppose that (A1), (A2), and ρ(D
-1
EU) < 1. Let
 be a unique equilibrium point of system (1). Furthermore, assume that the impulsive operators I
k
(·) and J
k
(·) satisfy
be a unique equilibrium point of system (1). Furthermore, assume that the impulsive operators I
k
(·) and J
k
(·) satisfy

Then the unique equilibrium point z* of system (1) is globally exponentially stable.
Proof. Let z(t) = (x
1(t), x
2(t), ..., x
n
(t), y
1(t), y
2(t), ...,y
m
(t))T be an arbitrary solution of system (1) with initial value (ϕ,ψ) and ϕ = (ϕ
1(t), ϕ
2(t), ..., ϕ
n
(t))T ∈ C([-σ, 0]; R
n ), ψ = (ψ
1 (t), ψ
2(t), ..., ψ
n
(t))T ∈ C([-τ, 0]; R
m ). Set  , i = 1, 2, ..., n, j = 1, 2, ..., m.
, i = 1, 2, ..., n, j = 1, 2, ..., m.
From (1) and (5), for t > 0, t ≠ t k , k = 1, 2, ..., we have

According to (A 3), we get

Using (A1), (A2), (A3), Definition 1.2, and Lemma 1.2, from (14) and (15), we have

Where  , t ≠ t
k
, k ∈ Z
+, i = 1,2, ..., n; j = 1,2, ..., m. and
, t ≠ t
k
, k ∈ Z
+, i = 1,2, ..., n; j = 1,2, ..., m. and

which implies that

Since ρ(D -1 EU) = ρ (F) < 1, it follows from Lemmas 1.1 and 1.3 that E n+m - D -1 EU is an M- matrix, therefore there exists a vector η = (η 1, η 2, ..., η n , ζ1, ζ2, ..., ζ m )T > (0, 0, ...,0, 0, 0, ..., 0)T such that

Hence

which implies that

We can choose a positive constant λ < 1 such that, for i = 1, 2, ...n; j = 1, 2, ..., m

For all t ∈ [- σ - τ, 0], we can choose a constant γ > 1 such that

For ∀ε > 0, set

Caculating the upper left derivative of V i (t) and W j (t), respecively, and noting that (19)

and

where  . i = 1, 2, ..., n; 2, ..., m. from (20) and (21), we have
. i = 1, 2, ..., n; 2, ..., m. from (20) and (21), we have

On the other hand, we claim that for all t > 0, t ≠ t k , k ∈ Z +, i = 1, 2,..., n; j = 1, 2,..., m.

By contrary, from (17) one of the following two cases must occur
-
(i)
there must exist i ∈ {1, 2,..., n} and
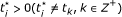 such that for l = 1, 2,..., n, k = 1, 2,..., m.
such that for l = 1, 2,..., n, k = 1, 2,..., m. 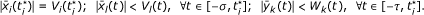 (26)
(26) -
(ii)
there must exist j ∈ {1, 2,..., m} and
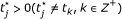 such that for l = 1, 2,..., n, k = 1, 2,..., m.
such that for l = 1, 2,..., n, k = 1, 2,..., m.  (27)
(27)
Suppose case (i) occurs, we obtain

In view of (16), (22) and (25), we have

which contradicts (28).
Suppose case (ii) occurs, we obtain

In view of (16), (23) and (27), we have

which contradicts (30). Therefore (25) holds.
Furthermore, together with (17) and (25), we have

where i = 1, 2, ..., n, j = 1, 2,..., m, k ∈ Z +.
Let ε → 0+, M = (n + m) max {max1 ≤ i ≤ n {γη i }, max1 ≤ i ≤ m {γζ j }} + 1, we have from (25) and (32) that

for all t > 0, i = 1, 2, ..., n; j = 1, 2, ..., m. The proof of theorem 3.1 is completed.
Corollary 3.1 Suppose (A 1), (A 2) and (A 3) hold, and if there exist some constants η i > 0(i = 1, 2, ..., n); ζ j > 0(j = 1, 2, ..., m), such that

Then system (1) has a unique equilibrium point z* which is globally exponentially stable.
Corollary 3.2 Let (A 1), (A 2) and (A 3) hold, and suppose that E n+m -D-1 EU is an M-matrix. Then system (1) has a unique equilibrium point z* which is globally exponentially stable.
An illustrative example
In this section, we give an example to illustrate the results obtained.
Example 4.1. Considering the following fuzzy BAM neural networks with constant delays.

where  , and t
1 < t
2 < ⋯ is strictly increasing sequences such that lim
k→∞
t
k
= +∞,
, and t
1 < t
2 < ⋯ is strictly increasing sequences such that lim
k→∞
t
k
= +∞,  .
.
So, by easy computation, we can see that system (35) satisfy the conditions (A 1), (A 2), (A 3), and ρ(D -1 EU) = 0.8917 < 1. Therefore, from Theorem 3.1, system (35) has an unique equilibrium point which is globally exponentially stable.
Conclusion
In this article, fuzzy BAM neural networks with distributed delays and impulse have been studied. Some sufficient conditions for the existence, uniqueness, and global exponential stability of equilibrium point have been obtained. The criteria of stability is simple and independent of time delay. It is only associated with the templates of system (1). Moreover, an example is given to illustrate the effectiveness of our results obtained.
Abbreviations
- BAM:
-
bi-directional associative memory
- FCNNs:
-
fuzzy cellular neural networks.
References
Kosto B: Adaptive bi-directional associative memories. Appl Opt 1987, 26: 4947-4960. 10.1364/AO.26.004947
Kosto B: Bi-directional associative memories. IEEE Trans Syst Man Cyber 1988, 18: 49-60. 10.1109/21.87054
Gopalsmy K, He XZ: Delay-independent stability in bi-directional associative memory networks. IEEE Trans Neural Netw 1994, 5: 998-1002. 10.1109/72.329700
Liu B, Huang L: Global exponential stability of BAM neural networks with recent-history distributed delays and impulse. Neurocomputing 2006, 69: 2090-2096. 10.1016/j.neucom.2005.09.014
Cao J, Wang L: Exponential stability and periodic oscilatory solution in BAM networks with delays. IEEE Trans Neural Netw 2002, 13: 457-463. 10.1109/72.991431
Zhao H: Global exponential stability of bidirectional associative memory neural networks with distributed delays. Phys Lett A 2002, 297: 182-190. 10.1016/S0375-9601(02)00434-6
Zhang J, Yang Y: Global stability analysis of bidirectional associative memory neural networks with time delay. Int J Ciruit Theor Appl 2001, 29: 185-196. 10.1002/cta.144
Liao XF, Wong KW, Yang SZ: Convergence dynamics of hybrid bidirectional associative memory neural networks with distributed delays. Phys Lett A 2003, 316: 55-64. 10.1016/S0375-9601(03)01113-7
Liao XF, Yu JB: Qualitative analysis of bi-directional associative memory with time delay. Int J Circ Theory Appl 1988, 26: 219-229.
Cao J, Jiang Q: An analysis of periodic solutions of bi-directional associative memory networks with time-varying delays. Phys Lett A 2004, 330: 203-213. 10.1016/j.physleta.2004.07.064
Chen A, Cao J, Huang L: Exponential stability of BAM neural networks with transmission delays. Neurocomputing 2004, 57: 435-454.
Chen A, Huang L, Cao J: Existence and stability of almost periodic solution for BAM neural networks with delays. Appl Math Comput 2003, 137: 177-193. 10.1016/S0096-3003(02)00095-4
Chen A, Huang L, Liu Z, Cao J: Periodic bidirectional associative memory neural networks with distributed delays. J Math Anal Appl 2006, 317: 80-102. 10.1016/j.jmaa.2005.09.092
Liu Z, Chen A, Cao J, Huang L: Existence and global exponential stability of almost periodic solutions of BAM neural networks with continuously distributed delays. Phys Lett A 2003, 319: 305-316. 10.1016/j.physleta.2003.10.020
Guo SJ, Huang L, Dai B, Zhang Z: Global existence of periodic solutions of BAM neural networks with variable coefficients. Phys Lett A 2003, 317: 97-106. 10.1016/j.physleta.2003.08.019
Cao J: A set of stability criteria for delayed cellular neural networks. IEEE Trans Circuits Syst I 2001, 48: 494-498. 10.1109/81.917987
Cao J: Global stability conditions for delayed CNNs. IEEE Trans Circuits Syst I 2001, 48: 1330-1333. 10.1109/81.964422
Cao J, Wang J: Global asymptotic stability of general class of recurrent neural networks with time-varying delays. IEEE Trans Circuits Syst I 2003, 50: 34-44. 10.1109/TCSI.2002.807494
Cao J: New results concerning exponential stability and periodic solutions of delayed cellular neural networks. Phys Lett A 2003, 307: 136-147. 10.1016/S0375-9601(02)01720-6
Cao J, Wang J: Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays. Neural Netw 2004, 17: 379-390. 10.1016/j.neunet.2003.08.007
Cao J, Wang J: Global exponential stability and periodicity of recurrent neural networks with time delays. IEEE Trans Circuits Syst I 2005, 52: 920-931.
Cao J, Ho DWC: A general framework for global asymptotic stability analysis of delayed neural networks based on LMI approach. Chaos Solitons Fract 2005, 24: 1317-1329. 10.1016/j.chaos.2004.09.063
Cao J, Huang D, Qu Y: Global robust stability of delayed recurrent neural networks. Chaos Solitons Fract 2005, 23: 221-229. 10.1016/j.chaos.2004.04.002
Yang T, Yang L: The global stability of fuzzy cellular neural networks. IEEE Trans Circuit Syst I 1996, 43: 880-883. 10.1109/81.538999
Yang T, Yang L, Wu C, Chua L: Fuzzy cellular neural networks: theory. Proceedings of the IEEE International Workshop on Cellular Neural Networks Application 1996, 181-186.
Yang T, Yang L, Wu C, Chua L: Fuzzy cellular neural networks: applications. Proceedings of IEEE International Workshop on Cellular Neural Neworks Application 1996, 225-230.
Huang T: Exponential stability of fuzzy cellular neural networks with distributed delay. Phys Lett A 2006, 351: 48-52. 10.1016/j.physleta.2005.10.060
Huang T: Exponential stability of delayed fuzzy cellular neural networks with diffusion. Chaos Solitons Fract 2007, 31: 658-664. 10.1016/j.chaos.2005.10.015
Yuan K, Cao J, Deng J: Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays. Neurocomputing 2006, 69: 1619-1627. 10.1016/j.neucom.2005.05.011
Zhang Q, Xiang R: Global asymptotic stability of fuzzy cellular neural networks with time-varying delays. Phys Lett A 2008, 372: 3971-3977. 10.1016/j.physleta.2008.01.063
Lakshmikantham V, Bainov DD, Simeonov P: Theory of impulsive differential equations. World Sceintific, Singaore 1989.
Liu X, Ballinger G: Existence and continuability of solutions for differential equations with delays and state-dependent impulses. Nonlinear Anal 2002, 51: 633-647. 10.1016/S0362-546X(01)00847-1
Yan JR, Zhao A, Yan W: Existence and global attractivity of periodic solution for an impulsive delay differential equation with Allee effect. J Math Anal Appl 2005, 309: 489-504. 10.1016/j.jmaa.2004.09.038
Li YK: Global exponential stability of BAM neural networks with delays and impulses. Chaos, Solitons Fract 2005, 24: 279-285.
Li YK, Gao S: Global exponential stability for impulsive BAM neural networks with distributed delays on time scales. Neural Process Lett 2010, 31: 65-91. 10.1007/s11063-009-9127-z
Acknowledgements
This work is partially supported by the Doctoral Foundation of Guizhou College of Finance and Economics(2010), the Scientific Research Foundation of Guizhou Science and Technology Department(Dynamics of Impulsive Fuzzy Cellular Neural Networks with Delays[2011]J2096), and by the Scientific Research Foundation of Hunan Provincial Education Department(10B023). The authors would like to thank the Editor and the referees for their helpful comments and valuable suggestions regarding this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
The authors indicated in parentheses made substantial contributions to the following tasks of research: drafting the manuscript.(L.H.Y); participating in the design of the study (D.X.L); writing and revision of paper (Q.H.Z, L.H.Y).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, Q., Yang, L. & Liao, D. Existence and globally exponential stability of equilibrium for fuzzy BAM neural networks with distributed delays and impulse. Adv Differ Equ 2011, 8 (2011). https://doi.org/10.1186/1687-1847-2011-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2011-8
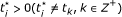 such that for l = 1, 2,..., n, k = 1, 2,..., m.
such that for l = 1, 2,..., n, k = 1, 2,..., m. 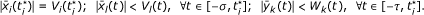
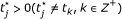 such that for l = 1, 2,..., n, k = 1, 2,..., m.
such that for l = 1, 2,..., n, k = 1, 2,..., m. 