- Research Article
- Open access
- Published:
On the Existence of Solutions for Dynamic Boundary Value Problems under Barrier Strips Condition
Advances in Difference Equations volume 2011, Article number: 378686 (2011)
Abstract
By defining a new terminology, scatter degree, as the supremum of graininess functional value, this paper studies the existence of solutions for a nonlinear two-point dynamic boundary value problem on time scales. We do not need any growth restrictions on nonlinear term of dynamic equation besides a barrier strips condition. The main tool in this paper is the induction principle on time scales.
1. Introduction
Calculus on time scales, which unify continuous and discrete analysis, is now still an active area of research. We refer the reader to [1–5] and the references therein for introduction on this theory. In recent years, there has been much attention focused on the existence and multiplicity of solutions or positive solutions for dynamic boundary value problems on time scales. See [6–17] for some of them. Under various growth restrictions on nonlinear term of dynamic equation, many authors have obtained many excellent results for the above problem by using Topological degree theory, fixed-point theorems on cone, bifurcation theory, and so on.
In 2004, Ma and Luo [18] firstly obtained the existence of solutions for the dynamic boundary value problems on time scales

under a barrier strips condition. A barrier strip  is defined as follows. There are pairs (two or four) of suitable constants such that nonlinear term
is defined as follows. There are pairs (two or four) of suitable constants such that nonlinear term  does not change its sign on sets of the form
does not change its sign on sets of the form  , where
, where  is a nonnegative constant, and
is a nonnegative constant, and  is a closed interval bounded by some pairs of constants, mentioned above.
is a closed interval bounded by some pairs of constants, mentioned above.
The idea in [18] was from Kelevedjiev [19], in which discussions were for boundary value problems of ordinary differential equation. This paper studies the existence of solutions for the nonlinear two-point dynamic boundary value problem on time scales

where  is a bounded time scale with
is a bounded time scale with  ,
, , and
, and  . We obtain the existence of at least one solution to problem (1.2) without any growth restrictions on
. We obtain the existence of at least one solution to problem (1.2) without any growth restrictions on  but an existence assumption of barrier strips. Our proof is based upon the well-known Leray-Schauder principle and the induction principle on time scales.
but an existence assumption of barrier strips. Our proof is based upon the well-known Leray-Schauder principle and the induction principle on time scales.
The time scale-related notations adopted in this paper can be found, if not explained specifically, in almost all literature related to time scales. Here, in order to make this paper read easily, we recall some necessary definitions here.
A time scale  is a nonempty closed subset of
is a nonempty closed subset of  ; assume that
; assume that  has the topology that it inherits from the standard topology on
has the topology that it inherits from the standard topology on  . Define the forward and backward jump operators
. Define the forward and backward jump operators  by
by

In this definition we put  ,
, . Set
. Set  ,
, . The sets
. The sets  and
and  which are derived from the time scale
which are derived from the time scale  are as follows:
are as follows:

Denote interval  on
on  by
by  .
.
Definition 1.1.
If  is a function and
is a function and  , then the delta derivative of
, then the delta derivative of  at the point
at the point  is defined to be the number
is defined to be the number  (provided it exists) with the property that, for each
(provided it exists) with the property that, for each  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

for all  . The function
. The function  is called
is called  -differentiable on
-differentiable on  if
if  exists for all
exists for all  .
.
Definition 1.2.
If  holds on
holds on  , then we define the Cauchy
, then we define the Cauchy  -integral by
-integral by

Lemma 1.3 (see [2, Theorem 1.16 (SUF)]).
If  is
is  -differentiable at
-differentiable at  , then
, then

Lemma 1.4 (see [18, Lemma 3.2]).
Suppose that  is
is  -differentiable on
-differentiable on  , then
, then
(i) is nondecreasing on
is nondecreasing on  if and only if
if and only if  ,
,
(ii) is nonincreasing on
is nonincreasing on  if and only if
if and only if  .
.
Lemma 1.5 (see [4, Theorem 1.4]).
Let  be a time scale with
be a time scale with  . Then the induction principle holds.
. Then the induction principle holds.
Assume that, for a family of statements  ,
, , the following conditions are satisfied.
, the following conditions are satisfied.
(1) holds true.
holds true.
(2)For each  with
with  , one has
, one has  .
.
(3)For each  with
with  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that  for all
for all  ,
, .
.
(4)For each  with
with  , one has
, one has  for all
for all  .
.
Then  is true for all
is true for all  .
.
Remark 1.6.
For  , we replace
, we replace  with
with  and
and  with
with  , substitute < for >, then the dual version of the above induction principle is also true.
, substitute < for >, then the dual version of the above induction principle is also true.
By  , we mean the Banach space of second-order continuous
, we mean the Banach space of second-order continuous  -differentiable functions
-differentiable functions  equipped with the norm
equipped with the norm

where  ,
,  ,
,  . According to the well-known Leray-Schauder degree theory, we can get the following theorem.
. According to the well-known Leray-Schauder degree theory, we can get the following theorem.
Lemma 1.7.
Suppose that  is continuous, and there is a constant
is continuous, and there is a constant  , independent of
, independent of  , such that
, such that  for each solution
for each solution  to the boundary value problem
to the boundary value problem

Then the boundary value problem (1.2) has at least one solution in  .
.
Proof.
The proof is the same as [18, Theorem 4.1].
2. Existence Theorem
To state our main result, we introduce the definition of scatter degree.
Definition 2.1.
For a time scale  , define the right direction scatter degree (RSD) and the left direction scatter degree (LSD) on
, define the right direction scatter degree (RSD) and the left direction scatter degree (LSD) on  by
by

respectively. If  , then we call
, then we call  (or
(or  ) the scatter degree on
) the scatter degree on  .
.
Remark 2.2.
-
(1)
If
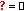 , then
, then 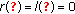 . If
. If  , then
, then 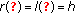 . If
. If 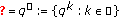 and
and 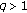 , then
, then 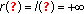 . (2) If
. (2) If  is bounded, then both
is bounded, then both 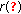 and
and 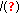 are finite numbers.
are finite numbers.
Theorem 2.3.
Let  be continuous. Suppose that there are constants
be continuous. Suppose that there are constants  ,
, , with
, with  ,
,  satisfying
satisfying
-
(H1)
 ,
, ,
, -
(H2)
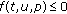 for
for 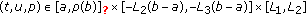 ,
, 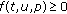 for
for 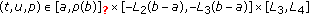 ,
,
where

Then problem (1.2) has at least one solution in  .
.
Remark 2.4.
Theorem 2.3 extends [19, Theorem 3.2] even in the special case  . Moreover, our method to prove Theorem 2.3 is different from that of [19].
. Moreover, our method to prove Theorem 2.3 is different from that of [19].
Remark 2.5.
We can find some elementary functions which satisfy the conditions in Theorem 2.3. Consider the dynamic boundary value problem

where  is bounded everywhere and continuous.
is bounded everywhere and continuous.
Suppose that  , then for
, then for 

It implies that there exist constants  ,
, , satisfying (H1) and (H2) in Theorem 2.3. Thus, problem (2.3) has at least one solution in
, satisfying (H1) and (H2) in Theorem 2.3. Thus, problem (2.3) has at least one solution in  .
.
Proof of Theorem 2.3.
Define  as follows:
as follows:

For all  , suppose that
, suppose that  is an arbitrary solution of problem
is an arbitrary solution of problem

We firstly prove that there exists  , independent of
, independent of  and
and  , such that
, such that  .
.
We show at first that

Let  ,
, . We employ the induction principle on time scales (Lemma 1.5) to show that
. We employ the induction principle on time scales (Lemma 1.5) to show that  holds step by step.
holds step by step.
-
(1)
From the boundary condition
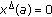 and the assumption of
and the assumption of  ,
,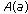 holds.
holds. -
(2)
For each
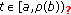 with
with 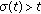 , suppose that
, suppose that  holds, that is,
holds, that is, 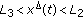 . Note that
. Note that  ; we divide this discussion into three cases to prove that
; we divide this discussion into three cases to prove that 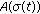 holds.
holds.
Case 1.
If  , then from Lemma 1.3, Definition 2.1, and (H1) there is
, then from Lemma 1.3, Definition 2.1, and (H1) there is

Similarly,  .
.
Case 2.
If  , then similar to Case 1 we have
, then similar to Case 1 we have

Suppose to the contrary that  , then
, then

which contradicts (H2). So  .
.
Case 3.
If  , similar to Case 2, then
, similar to Case 2, then  holds.
holds.
Therefore,  is true.
is true.
-
(3)
For each
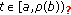 , with
, with 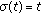 , and
, and  holds, then there is a neighborhood
holds, then there is a neighborhood  of
of 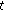 such that
such that  holds for all
holds for all  ,
, 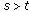 by virtue of the continuity of
by virtue of the continuity of 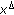 .
. -
(4)
(4)For each
 , with
, with 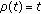 , and
, and 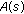 is true for all
is true for all 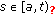 , since
, since  implies that
implies that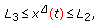 (2.11)
(2.11)we only show that
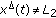 and
and  .
.
Suppose to the contrary that  . From
. From

 , and the continuity of
, and the continuity of  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

So  ,
,  . Combining with
. Combining with  ,
,  , we have from (H2),
, we have from (H2),  ,
,  ,
,  . So from Lemma 1.4
. So from Lemma 1.4

This contradiction shows that  . In the same way, we claim that
. In the same way, we claim that  .
.
Hence,  ,
,  , holds. So
, holds. So

From Definition 1.2 and Lemma 1.3, we have for 

There are, from  and (2.7),
and (2.7),

for  . In addition,
. In addition,

Thus,

that is,

Moreover, by the continuity of  , the equation in (2.6), (2.7) and the definition of
, the equation in (2.6), (2.7) and the definition of 

where  is defined in (2.2). Now let
is defined in (2.2). Now let  . Then, from (2.15), (2.20), and (2.21),
. Then, from (2.15), (2.20), and (2.21),

Note that from (2.19) we have

that is,  ,
,  . So
. So  is also an arbitrary solution of problem
is also an arbitrary solution of problem

According to (2.22) and Lemma 1.7, the dynamic boundary value problem (1.2) has at least one solution in  .
.
3. An Additional Result
Parallel to the definition of delta derivative, the notion of nabla derivative was introduced, and the main relations between the two operations were studied in [7]. Applying to the dual version of the induction principle on time scales (Remark 1.6), we can obtain the following result.
Theorem 3.1.
Let  be continuous. Suppose that there are constants
be continuous. Suppose that there are constants  ,
,  , with
, with  ,
,  satisfying
satisfying
-
(S1)
 ,
, 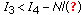 ,
, -
(S2)
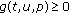 for
for 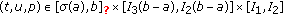 ,
, 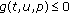 for
for 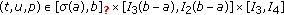 ,
,
where

Then dynamic boundary value problem

has at least one solution.
Remark 3.2.
According to Theorem 3.1, the dynamic boundary value problem related to the nabla derivative

has at least one solution. Here  is bounded everywhere and continuous.
is bounded everywhere and continuous.
References
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Kaymakcalan B, Lakshmikantham V, Sivasundaram S: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Agarwal RP, O'Regan D: Triple solutions to boundary value problems on time scales. Applied Mathematics Letters 2000,13(4):7-11. 10.1016/S0893-9659(99)00200-1
Atici FM, Guseinov GS: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002,141(1-2):75-99. Special issue on "Dynamic equations on time scales", edited by R. P. Agarwal, M. Bohner and D. O'Regan 10.1016/S0377-0427(01)00437-X
Bohner M, Luo H: Singular second-order multipoint dynamic boundary value problems with mixed derivatives. Advances in Difference Equations 2006, 2006:-15.
Chyan CJ, Henderson J: Twin solutions of boundary value problems for differential equations on measure chains. Journal of Computational and Applied Mathematics 2002,141(1-2):123-131. Special issue on "Dynamic equations on time scales", edited by R. P. Agarwal, M. Bohner and D. O'Regan 10.1016/S0377-0427(01)00440-X
Erbe L, Peterson A, Mathsen R: Existence, multiplicity, and nonexistence of positive solutions to a differential equation on a measure chain. Journal of Computational and Applied Mathematics 2000,113(1-2):365-380. 10.1016/S0377-0427(99)00267-8
Gao C, Luo H: Positive solutions to nonlinear first-order nonlocal BVPs with parameter on time scales. Boundary Value Problems 2011, 2011:-15.
Henderson J:Multiple solutions for
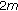 order Sturm-Liouville boundary value problems on a measure chain. Journal of Difference Equations and Applications 2000,6(4):417-429. 10.1080/10236190008808238
order Sturm-Liouville boundary value problems on a measure chain. Journal of Difference Equations and Applications 2000,6(4):417-429. 10.1080/10236190008808238Li W-T, Sun H-R: Multiple positive solutions for nonlinear dynamical systems on a measure chain. Journal of Computational and Applied Mathematics 2004,162(2):421-430. 10.1016/j.cam.2003.08.032
Luo H, Ma R: Nodal solutions to nonlinear eigenvalue problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2006,65(4):773-784. 10.1016/j.na.2005.09.043
Sun H-R:Triple positive solutions for
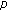 -Laplacian
-Laplacian 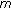 -point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083
-point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083Sun J-P, Li W-T: Existence and nonexistence of positive solutions for second-order time scale systems. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):3107-3114. 10.1016/j.na.2007.03.003
Wang D-B, Sun J-P, Guan W: Multiple positive solutions for functional dynamic equations on time scales. Computers & Mathematics with Applications 2010,59(4):1433-1440. 10.1016/j.camwa.2009.12.019
Ma R, Luo H: Existence of solutions for a two-point boundary value problem on time scales. Applied Mathematics and Computation 2004,150(1):139-147. 10.1016/S0096-3003(03)00204-2
Kelevedjiev P: Existence of solutions for two-point boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1994,22(2):217-224. 10.1016/0362-546X(94)90035-3
Acknowledgments
H. Luo was supported by China Postdoctoral Fund (no. 20100481239), the NSFC Young Item (no. 70901016), HSSF of Ministry of Education of China (no. 09YJA790028), Program for Innovative Research Team of Liaoning Educational Committee (no. 2008T054), and Innovation Method Fund of China (no. 2009IM010400-1-39). Y. An was supported by 11YZ225 and YJ2009-16 (A06/1020K096019).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Luo, H., An, Y. On the Existence of Solutions for Dynamic Boundary Value Problems under Barrier Strips Condition. Adv Differ Equ 2011, 378686 (2011). https://doi.org/10.1155/2011/378686
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/378686
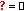 , then
, then 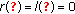 . If
. If  , then
, then 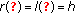 . If
. If 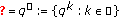 and
and 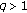 , then
, then 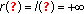 . (2) If
. (2) If  is bounded, then both
is bounded, then both 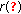 and
and 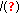 are finite numbers.
are finite numbers. ,
, ,
,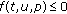 for
for 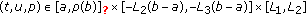 ,
, 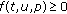 for
for 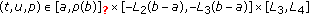 ,
,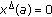 and the assumption of
and the assumption of  ,
,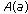 holds.
holds.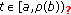 with
with 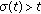 , suppose that
, suppose that  holds, that is,
holds, that is, 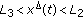 . Note that
. Note that  ; we divide this discussion into three cases to prove that
; we divide this discussion into three cases to prove that 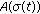 holds.
holds.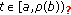 , with
, with 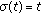 , and
, and  holds, then there is a neighborhood
holds, then there is a neighborhood  of
of 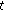 such that
such that  holds for all
holds for all  ,
, 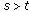 by virtue of the continuity of
by virtue of the continuity of 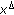 .
. , with
, with 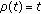 , and
, and 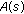 is true for all
is true for all 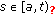 , since
, since  implies that
implies that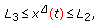
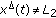 and
and  .
. ,
, 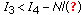 ,
,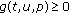 for
for 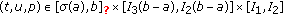 ,
, 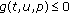 for
for 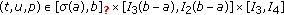 ,
, order Sturm-Liouville boundary value problems on a measure chain. Journal of Difference Equations and Applications 2000,6(4):417-429. 10.1080/10236190008808238
order Sturm-Liouville boundary value problems on a measure chain. Journal of Difference Equations and Applications 2000,6(4):417-429. 10.1080/10236190008808238 -Laplacian
-Laplacian  -point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083
-point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083