- Research Article
- Open access
- Published:
Employing of Some Basic Theory for Class of Fractional Differential Equations
Advances in Difference Equations volume 2011, Article number: 296353 (2011)
Abstract
Basic theory on a class of initial value problem of some fractional differential equation involving Riemann-Liouville differential operators is discussed by employing the classical approach from the work of Lakshmikantham and A. S. Vatsala (2008). The theory of inequalities, local existence, extremal solutions, comparison result and global existence of solutions are considered. Our work employed recent literature from the work of (Lakshmikantham and A. S. Vatsala, (2008)).
1. Introduction
Differential equations of fractional order have recently proven to be valuable tools in the modeling of many phenomena in various fields of science and engineering. Indeed, we can find numerous applications in viscoelasticity, electrochemistry, control, porous media, electromagnetism, and so forth [1–5]. There has been a significant development in the study of fractional differential equations and inclusions in recent years; see the monographs of Kilbas et al. [6], Lakshmikantham et al. [7], Podlubny [4], and the survey by Agarwal et al. [8]. For some recent contributions on fractional differential equations, see [9–20] and the references therein. Very recently in [10, 11, 21, 22], the author and other researchers studied the existence and uniqueness of solutions of some classes of fractional differential equations with delay. For more details on the geometric and physical interpretation for fractional derivatives of both the Caputo types see [5, 23]. Băleanu and Mustafa [16] allowed for immediate applications of a general comparison-type result from the recent literature [24]. Lakshmikantham and Vatsal have discussed basic theory of fractional differential equations for initial value problem fractional differential equations type [24]

This paper deals with the basic theory of initial value problem (IVP) for a generalized class of fractional order differential equation of the form

where  and
and  . Recall that
. Recall that  is the Banach space of continuous functions from the interval
is the Banach space of continuous functions from the interval  into
into  endowed with uniform norm.
endowed with uniform norm.
We begin in this section with the recall of some definitions and results for fractional calculus which are used throughout this paper [4, 19, 20].
The left-sided Riemann-Liouville fractional integral of a function  of order
of order  is defined as
is defined as

and the left sided Riemann-Liouville fractional derivative operator of order  is defined by
is defined by

where  . We denote
. We denote  by
by  and
and  by
by  . Also
. Also  and
and  refer to
refer to  and
and  , respectively.
, respectively.
Assume that  , if the fractional derivative
, if the fractional derivative  is integrable, then [4, page 72]
is integrable, then [4, page 72]

If  is continuous on
is continuous on  then
then  is integrable,
is integrable,  [25], and (1.5) reduces to
[25], and (1.5) reduces to

Proposition 1.1.
Let  and
and  . Then
. Then 
-
(i)
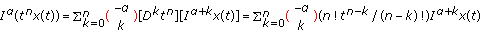 ,
, -
(ii)
 ,
,
where  is a nonnegative integer, and
is a nonnegative integer, and

Proof.
-
(i)
can be found in [19, page 53] and (ii) is an immediate consequence of (1.6) and (i).
2. Strict and Nonstrict Inequalities
Since  is assumed to be continuous, the initial value problem (1.2) is equivalent to the following Volterra fractional integral [10, 25]:
is assumed to be continuous, the initial value problem (1.2) is equivalent to the following Volterra fractional integral [10, 25]:

Note.
Let us consider the notation of  for second term in (2.1) which is used in throughout of text and so that
for second term in (2.1) which is used in throughout of text and so that

We now first discuss a fundamental result relative to the fractional inequalities.
Theorem 2.1.
Let  ,
,  , and
, and
-
(i)
 ,
, -
(ii)
 ,
,
one of the foregoing inequalities being strict. Moreover, if  is nondecreasing in
is nondecreasing in  for each
for each  and
and  , then one has
, then one has .
.
Proof.
Suppose that for each  , the conclusion
, the conclusion  is not true. Then, because of the continuity of the functions involved and
is not true. Then, because of the continuity of the functions involved and  it follows that there exists a
it follows that there exists a  such that
such that  and
and

Let us suppose that the inequality (ii) is strict. Then using the nondecreasing nature of  and (2.3) we get
and (2.3) we get

which is a contradiction in view of (2.3). Hence the conclusion of this theorem holds and the proof is complete.
The next result is for nonstrict inequalities, which require a one-sided Lipschitz type condition.
Theorem 2.2.
Assume that the conditions of Theorem 2.1 hold with nonstrict inequalities (i) and (ii). Suppose further that

whenever  and
and  . Then,
. Then,  , and
, and  implies
implies

Proof.
Set  , for small
, for small  so that we have,
so that we have,

Now,

In view of (2.7), using one-sided Lipschitz condition (2.5) we see that

Now, since  , we arrive at
, we arrive at

in view of the condition  . We now apply Theorem 2.1 to the inequalities (i), (2.9), and (2.10) to get
. We now apply Theorem 2.1 to the inequalities (i), (2.9), and (2.10) to get  ,
,  . Since
. Since  is arbitrary, we conclude that (2.6) is true, and we are done.
is arbitrary, we conclude that (2.6) is true, and we are done.
3. Local Existence and Extremal Conditions
In this section, we will consider the local existence and the existence of extremal solutions for the IVP (1.2). We now first discuss Peano's type existence result.
Theorem 3.1.
Assume that  , where
, where  , and let
, and let  on
on  . Then the IVP (1.2) has at least one solution
. Then the IVP (1.2) has at least one solution  on
on  , where
, where

so that  and
and  will be observing in the proof of this theorem.
will be observing in the proof of this theorem.
Proof.
Let be a continuous function on
be a continuous function on such that
such that  . For
. For  , we define a function
, we define a function  on
on  and
and

on  , where
, where  . We observe that
. We observe that

where

Note that,  , as
, as  . Then
. Then  , and hence we can consider
, and hence we can consider  in the last above inequality. Thus
in the last above inequality. Thus  .
.

because of the choice of  . If
. If  , we can employ (3.2) to extend as a continuous function on
, we can employ (3.2) to extend as a continuous function on  , such that
, such that  holds. Continuing this process, we can define
holds. Continuing this process, we can define  over
over  so that
so that  is satisfied on
is satisfied on  . Furthermore, letting
. Furthermore, letting  we see that
we see that

Notice that  and
and  , when
, when  . Let,
. Let,

firstly we have

We, therefore, set , and get
, and get

Finally, inequality (3.6) from inequality (3.9) becomes

provided that

It then follows from (3.4) and (3.6) that the family  forms an equicontinuous and uniformly bounded functions. Ascoli-Arzela theorem implies that the existence of a sequence
forms an equicontinuous and uniformly bounded functions. Ascoli-Arzela theorem implies that the existence of a sequence  such that
such that  as
as  , and
, and  exists uniformly on
exists uniformly on  . Since
. Since  is uniformly continuous, we obtain that
is uniformly continuous, we obtain that  tends uniformly to
tends uniformly to  as
as  , and, hence, term by term integration of (3.2) with
, and, hence, term by term integration of (3.2) with  yields
yields

This proves that  is a solution of the IVP (1.2), and the proof is complete.
is a solution of the IVP (1.2), and the proof is complete.
Theorem 3.2.
Under the hypothesis of Theorem 3.1, there exists extremal solution for the IVP (1.2) on the interval  , provided
, provided  is nondecreasing in
is nondecreasing in  for each
for each  , where
, where  will be observed in the proof of this theorem.
will be observed in the proof of this theorem.
Proof.
We will prove the existence of maximal solution only, since the case of minimal solution is very similar. Let  and consider the fractional differential equation with an initial condition
and consider the fractional differential equation with an initial condition

We observe that  is defined and continuous on
is defined and continuous on

 and
and  on
on  . We then deduce from Theorem 3.1 that IVP (3.6) has a solution
. We then deduce from Theorem 3.1 that IVP (3.6) has a solution  on the interval
on the interval  . Now for
. Now for  , we have
, we have

where  was introduced by (2.2). In view of Theorem 2.1 to get
was introduced by (2.2). In view of Theorem 2.1 to get  . Consider the family of functions
. Consider the family of functions  on
on  . We have
. We have

where  was denoted by (3.4),
was denoted by (3.4),  and
and

Showing that the family  is uniformly bounded. Also, if
is uniformly bounded. Also, if  then there exists a constant
then there exists a constant  such that
such that

Following the computation similar to (3.10) with suitable changes. This proves that the family  is equicontinuous. Hence there exists a sequence
is equicontinuous. Hence there exists a sequence  with
with  as
as  and the uniform limit
and the uniform limit

exists on  . Clearly
. Clearly  . The uniform continuity of
. The uniform continuity of  gives argument as before (as in Theorem 3.1), that
gives argument as before (as in Theorem 3.1), that  is a solution of IVP (1.2).
is a solution of IVP (1.2).
Next, we show that  is required maximal solution of (1.2), on
is required maximal solution of (1.2), on  . Let
. Let  be a any solution of (1.2) on
be a any solution of (1.2) on  . Then we have
. Then we have

where  ,
,  , and
, and  .
.
Using Theorem 2.1, we get  on
on  as
as  . Therefore, the proof is complete.
. Therefore, the proof is complete.
4. Global Existence
We need the following comparison result before we proceed further.
Theorem 4.1.
Assume that  ,
,  are continuous, and
are continuous, and  is nondecreasing with respect to the second argument such that
is nondecreasing with respect to the second argument such that

where  is defined by (3.5). Let
is defined by (3.5). Let  be the maximal solution of
be the maximal solution of

existing on  such that
such that  . Then we have
. Then we have

Proof.
In view of the definition of the maximal solution  , it is enough to prove, to conclude (4.3), that
, it is enough to prove, to conclude (4.3), that

where  is any solution of
is any solution of

Now, it follows from (4.4) that

where  . Then applying Theorem 2.1, we get immediately (4.1) and since
. Then applying Theorem 2.1, we get immediately (4.1) and since  uniformly on each
uniformly on each  , the proof is complete.
, the proof is complete.
We are now in position to prove global existence result.
Theorem 4.2.
Assume that  continuous. Let there exists function
continuous. Let there exists function  continuous and nondecreasing with respect to the second argument such that
continuous and nondecreasing with respect to the second argument such that

If the maximal solution of the initial value problem

exists in  then all solutions of the initial value problem
then all solutions of the initial value problem

with  exist in
exist in  .
.
Proof.
Let  be any solution of IVP (4.8) such that
be any solution of IVP (4.8) such that  , which exists on
, which exists on  for
for  , and the value of
, and the value of  cannot be increased further. Set
cannot be increased further. Set  for
for  . Then using the assumption (4.4), we get
. Then using the assumption (4.4), we get

Applying the comparison Theorem 4.1, we obtain

Since  is assumed to exist on
is assumed to exist on  , it follows that
, it follows that

Now, let  . Then employing the arguments similar to estimating (3.19) and using (4.7) and the bounded
. Then employing the arguments similar to estimating (3.19) and using (4.7) and the bounded  of
of  we arrive at
we arrive at

Letting  and using Cauchy criterion, it follows that
and using Cauchy criterion, it follows that  exists. We define
exists. We define  and consider the new IVP
and consider the new IVP

By the assumed local existence, we find that  can be continued beyond
can be continued beyond  , contradicting our assumption. Hence, every solution
, contradicting our assumption. Hence, every solution  of (4.9) exists on
of (4.9) exists on  , and the proof is complete.
, and the proof is complete.
References
Glockle WG, Nonnenmacher TF: A fractional calculus approach to self-similar protein dynamics. Biophysical Journal 1995,68(1):46-53. 10.1016/S0006-3495(95)80157-8
Hilfe R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Metzler R, Schick W, Kilian H-G, Nonnenmacher TF: Relaxation in filled polymers: a fractional calculus approach. The Journal of Chemical Physics 1995,103(16):7180-7186. 10.1063/1.470346
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Podlubny I: Geometric and physical interpretation of fractional integration and fractional differentiation. Fractional Calculus & Applied Analysis 2002,5(4):367-386.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Lakshmikantham V, Leela S, Vasundhara J: Theory of Fractional Dynamic Systems. Cambridge Academic, Cambridge, UK; 2009.
Agarwal RP, Benchohra M, Hamani S: A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions. Acta Applicandae Mathematicae 2010,109(3):973-1033. 10.1007/s10440-008-9356-6
Daftardar-Gejji V, Babakhani A: Analysis of a system of fractional differential equations. Journal of Mathematical Analysis and Applications 2004,293(2):511-522. 10.1016/j.jmaa.2004.01.013
Babakhani A, Enteghami E: Existence of positive solutions for multiterm fractional differential equations of finite delay with polynomial coefficients. Abstract and Applied Analysis 2009, 2009:-12.
Babakhani A: Positive solutions for system of nonlinear fractional differential equations in two dimensions with delay. Abstract and Applied Analysis 2010, 2010:-16.
Baleanu D, Golmankhaneh AK, Nigmatullin R, Golmankhaneh AK: Fractional Newtonian mechanics. Central European Journal of Physics 2010,8(1):120-125. 10.2478/s11534-009-0085-x
Baleanu D, Trujillo JI: A new method of finding the fractional Euler-Lagrange and Hamilton equations within Caputo fractional derivatives. Communications in Nonlinear Science and Numerical Simulation 2010,15(5):1111-1115. 10.1016/j.cnsns.2009.05.023
Baleanu D: New applications of fractional variational principles. Reports on Mathematical Physics 2008,61(2):199-206. 10.1016/S0034-4877(08)80007-9
Benchohra M, Hamani S, Ntouyas SK: Boundary value problems for differential equations with fractional order. Surveys in Mathematics and Its Applications 2008, 3: 1-12.
Băleanu D, Mustafa OG: On the global existence of solutions to a class of fractional differential equations. Computers & Mathematics with Applications 2010,59(5):1835-1841. 10.1016/j.camwa.2009.08.028
Chang Y-K, Nieto JJ: Some new existence results for fractional differential inclusions with boundary conditions. Mathematical and Computer Modelling 2009,49(3-4):605-609. 10.1016/j.mcm.2008.03.014
Ouahab A: Some results for fractional boundary value problem of differential inclusions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3877-3896. 10.1016/j.na.2007.10.021
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Gordon and Breach Science, Yverdon, Switzerland; 1993:xxxvi+976.
Belarbi A, Benchohra M, Ouahab A: Uniqueness results for fractional functional differential equations with infinite delay in Fréchet spaces. Applicable Analysis 2006,85(12):1459-1470. 10.1080/00036810601066350
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: Existence results for fractional order functional differential equations with infinite delay. Journal of Mathematical Analysis and Applications 2008,338(2):1340-1350. 10.1016/j.jmaa.2007.06.021
Heymans N, Podlubny I: Physical interpretation of initial conditions for fractional differential equations with Riemann-Liouville fractional derivatives. Rheologica Acta 2006,45(5):765-771. 10.1007/s00397-005-0043-5
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Babakhani A, Daftardar-Gejji V: Existence of positive solutions for multi-term non-autonomous fractional differential equations with polynomial coefficients. Electronic Journal of Differential Equations 2006, 2006: 129-12.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Babakhani, A., Baleanu, D. Employing of Some Basic Theory for Class of Fractional Differential Equations. Adv Differ Equ 2011, 296353 (2011). https://doi.org/10.1155/2011/296353
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/296353
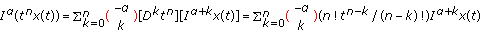 ,
, ,
, ,
, ,
,