- Research Article
- Open access
- Published:
Stability Analysis of Fractional Differential Systems with Order Lying in (1, 2)
Advances in Difference Equations volume 2011, Article number: 213485 (2011)
Abstract
The stability of  -dimensional linear fractional differential systems with commensurate order
-dimensional linear fractional differential systems with commensurate order  and the corresponding perturbed systems is investigated. By using the Laplace transform, the asymptotic expansion of the Mittag-Leffler function, and the Gronwall inequality, some conditions on stability and asymptotic stability are given.
and the corresponding perturbed systems is investigated. By using the Laplace transform, the asymptotic expansion of the Mittag-Leffler function, and the Gronwall inequality, some conditions on stability and asymptotic stability are given.
1. Introduction
Fractional calculus has a long history with more than three hundred years [1–3]. Up to now, it has been proved that fractional calculus is very useful. Many mathematical models of real problems arising in various fields of science and engineering were established with the help of fractional calculus, such as viscoelastic systems, dielectric polarization, electrode-electrolyte polarization, and electromagnetic waves [4–7].
Recently, the stability theory of fractional differential equations (FDEs) is of main interest in physical systems. Moreover, some stability results have been found [8–17]. These stability results are almost about the linear fractional differential systems with commensurate order (i.e., the fractional derivative order has to be an integer multiple of minimal fractional order [18]). For example, a necessary and sufficient condition on asymptotic stability of linear fractional differential system with order  was first given in [9]. Then, some literatures on the stability of linear fractional differential systems with order
was first given in [9]. Then, some literatures on the stability of linear fractional differential systems with order  have been appeared [11–15]. However, not all the fractional differential systems have fractional orders in (0, 1). There exist fractional models which have fractional orders lying in (1, 2), for example, super-diffusion [19]. Hence, the stability of linear fractional differential systems with order
have been appeared [11–15]. However, not all the fractional differential systems have fractional orders in (0, 1). There exist fractional models which have fractional orders lying in (1, 2), for example, super-diffusion [19]. Hence, the stability of linear fractional differential systems with order  has also been considered by using the conversion methods and transfer function [8, 10]. Almost all of the above literatures dealt with the fractional differential systems with Caputo derivative. Recently, Qian et al. [16] have investigated the stability of fractional differential systems with Riemann-Liouville derivative whose order
has also been considered by using the conversion methods and transfer function [8, 10]. Almost all of the above literatures dealt with the fractional differential systems with Caputo derivative. Recently, Qian et al. [16] have investigated the stability of fractional differential systems with Riemann-Liouville derivative whose order  lies in (0, 1) in details. It is worth mentioning that not all of the stability conditions are parallel to the corresponding classical integer-order differential equations because of nonlocality and weak singularities of fractional calculus. For example, the solution to an autonomous fractional differential equation cannot define a dynamical system in the sense of semigroup [20]. Of course, some of the mathematical tools for the integer-order differential equation can be applied to fractional kinetics. In [20], the authors first define the Lyapunov exponents for fractional differential system then determine their bounds, where the basic ideas and techniques are borrowed from [21, 22].
lies in (0, 1) in details. It is worth mentioning that not all of the stability conditions are parallel to the corresponding classical integer-order differential equations because of nonlocality and weak singularities of fractional calculus. For example, the solution to an autonomous fractional differential equation cannot define a dynamical system in the sense of semigroup [20]. Of course, some of the mathematical tools for the integer-order differential equation can be applied to fractional kinetics. In [20], the authors first define the Lyapunov exponents for fractional differential system then determine their bounds, where the basic ideas and techniques are borrowed from [21, 22].
In this paper, we study the stability of autonomous linear fractional differential systems, nonautonomous linear fractional differential systems, and the corresponding perturbed systems with order  by using the properties of Mittag-Leffler functions and the Gronwall inequality.
by using the properties of Mittag-Leffler functions and the Gronwall inequality.
The paper is organized as follows. In Section 2, we first recall some definitions and lemmas used throughout the paper. In Section 3, the stability analysis is presented for autonomous linear fractional differential systems with order  . The stability of nonautonomous linear fractional differential systems and the corresponding perturbed systems are studied in Sections 4 and 5, respectively. Conclusions and comments are included in Section 6.
. The stability of nonautonomous linear fractional differential systems and the corresponding perturbed systems are studied in Sections 4 and 5, respectively. Conclusions and comments are included in Section 6.
2. Preliminaries
Let us denote by  the set of real numbers, denote by
the set of real numbers, denote by  the set of positive real numbers, denote by
the set of positive real numbers, denote by  the set of positive integer numbers, and denote by
the set of positive integer numbers, and denote by  the set of complex numbers.
the set of complex numbers.
In this section, we recall the most commonly used definitions and properties of fractional derivatives, Mittag-Leffler functions, and their asymptotic expansions.
Definition 2.1.
The Riemann-Liouville derivative with order  of function
of function  is defined as follows:
is defined as follows:

where  ,
,  is the Gamma function.
is the Gamma function.
Definition 2.2.
The Caputo derivative with order  of function
of function  is defined as follows:
is defined as follows:

where  .
.
Their Laplace transforms for  are given as follows [23]:
are given as follows [23]:


Definition 2.3.
The Mittag-Leffler function is defined by

where the real part of  , that is,
, that is,  ,
,  . The two-parameter Mittag-Leffler function is defined by
. The two-parameter Mittag-Leffler function is defined by

where  and
and  ,
,  .
.
One can see  from the above equations. By analogy with (2.6), for
from the above equations. By analogy with (2.6), for  , we introduce a matrix Mittag-Leffler function defined by [24]
, we introduce a matrix Mittag-Leffler function defined by [24]

The following definitions of stability are introduced.
Definition 2.4.
The constant  is an equilibrium of fractional differential system
is an equilibrium of fractional differential system  if and only if
if and only if  for all
for all  , where the operator
, where the operator  denotes either
denotes either  or
or  .
.
Without loss of generality, let the equilibrium be  , we introduce the following definition.
, we introduce the following definition.
Definition 2.5.
The zero solution of  with order
with order  is said to be stable if, for any initial values
is said to be stable if, for any initial values  (
( ), there exists
), there exists  such that
such that  for all
for all  . The zero solution is said to be asymptotically stable if, in addition to being stable,
. The zero solution is said to be asymptotically stable if, in addition to being stable,  as
as  .
.
It is useful to recall the following asymptotic formulas for our developments in the sequel.
Lemma 2.6.
If  ,
,  is an arbitrary complex number and
is an arbitrary complex number and  is an arbitrary real number such that
is an arbitrary real number such that

then for an arbitrary integer  , the following expansions hold:
, the following expansions hold:

with  and
and

with  ,
,  .
.
Proof.
These results were proved in [23].
Especially, taking into account the Lemma 2.6 and derivatives of the Mittag-Leffler function, we obtain

with  ,
,  and
and

with  ,
,  ,
,  .
.
Lemma 2.7 (see [25]).
If  and
and  ,
,  is an arbitrary real number,
is an arbitrary real number,  satisfies
satisfies  , and
, and  is a real constant, then
is a real constant, then

where  ,
,  denotes the eigenvalues of matrix
denotes the eigenvalues of matrix  and
and  denotes the
denotes the  -norm.
-norm.
Lemma 2.8 (Jordan Decomposition [26]).
Let  be a square complex matrix, then there exists an invertible matrix
be a square complex matrix, then there exists an invertible matrix  such that
such that

where the  are the Jordan blocks of
are the Jordan blocks of  with the eigenvalues of
with the eigenvalues of  on the diagonal. The Jordan blocks are uniquely determined by
on the diagonal. The Jordan blocks are uniquely determined by  .
.
Lemma 2.9 (see [27]).
If

where all the functions involved are continuous on  ,
,  , and
, and  , then
, then  satisfies
satisfies

If, in addition,  is nondecreasing, then
is nondecreasing, then

3. Stability of Autonomous Linear Fractional Differential Systems
3.1. The Riemann-Liouville Derivative Case
In this subsection, we consider the following system of fractional differential equations:

with the initial conditions

where  , matrix
, matrix  , and
, and  . Then, by analyzing the solutions of the above initial value problem (3.1)-(3.2), one can find the following result.
. Then, by analyzing the solutions of the above initial value problem (3.1)-(3.2), one can find the following result.
Theorem 3.1.
The autonomous fractional differential system (3.1) with Riemann-Liouville derivative and the initial conditions (3.2) is asymptotically stable iff  . In this case, the components of the state decay towards 0 like
. In this case, the components of the state decay towards 0 like  . Moreover, the system (3.1) is stable iff either it is asymptotically stable, or those critical eigenvalues which satisfy
. Moreover, the system (3.1) is stable iff either it is asymptotically stable, or those critical eigenvalues which satisfy  have the same algebraic and geometric multiplicities.
have the same algebraic and geometric multiplicities.
Proof.
Applying the Laplace transform, we can get the solution of (3.1)-(3.2),

Firstly, we study the properties of the elements of matrixes  ,
,  . With regard to matrix
. With regard to matrix  , there exists an invertible matrix
, there exists an invertible matrix  , such that
, such that

from Lemma 2.8, where the Jordan block

 ,
,  is the eigenvalue of matrix
is the eigenvalue of matrix  and
and  . Substituting (3.4) into
. Substituting (3.4) into  , we yield
, we yield

where  . The matrix
. The matrix  can be written as follows by computing
can be written as follows by computing

where the operator  is given as follows:
is given as follows:

The nonzero elements of  can be described uniformly as
can be described uniformly as

-
(i)
If
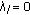 , then
, then  (3.10)
(3.10)
It is obvious that  (
( ) for
) for  and
and  . Thus,
. Thus,  (
( ).
).
-
(ii)
If
 , three cases will be considered separately.
, three cases will be considered separately.
Case 1 ( ).
).
If  and
and  , then
, then

That is to say,  (
( ) from the asymptotic expansion (2.12) and
) from the asymptotic expansion (2.12) and  (
( ). Moreover, the components of the state decay towards 0 like
). Moreover, the components of the state decay towards 0 like  . Taking into account the entire function
. Taking into account the entire function  , we also get the boundedness of
, we also get the boundedness of  (
( ;
;  ).
).
Case 2 ( ).
).
If  and
and  , from the asymptotic expansion (2.11), we have
, from the asymptotic expansion (2.11), we have

then

because of  , that is,
, that is,  .
.
So,  (
( ).
).
Case 3 ( ).
).
Let  , where
, where  is the modulus of
is the modulus of  and
and  .
.
Firstly, suppose that the critical eigenvalue  has the same algebraic and geometric multiplicities, that is, the matrix
has the same algebraic and geometric multiplicities, that is, the matrix  is a diagonal matrix, then, according to (3.7), we have
is a diagonal matrix, then, according to (3.7), we have

If  , we have the diagonal elements of matrix (3.14)
, we have the diagonal elements of matrix (3.14)  (
( ) from the asymptotic expansion (2.11). So, the solution of (3.1) is stable in this case.
) from the asymptotic expansion (2.11). So, the solution of (3.1) is stable in this case.
Next, suppose that the algebraic multiplicity of critical eigenvalue  is not equal to the geometric multiplicity, that is, the matrix
is not equal to the geometric multiplicity, that is, the matrix  is a Jordan block matrix, and matrix
is a Jordan block matrix, and matrix  is the same as (3.7), then the nondiagonal elements of
is the same as (3.7), then the nondiagonal elements of  can be evaluated from (3.12) as follows:
can be evaluated from (3.12) as follows:

So,

that is,  as
as  .
.
According to the above discussions, the proof is completed.
Remark 3.2.
-
(1)
If
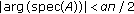 , then system (3.1) is not stable.
, then system (3.1) is not stable. -
(2)
If
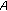 has zero eigenvalue, system (3.1) is not stable.
has zero eigenvalue, system (3.1) is not stable. -
(3)
If
 has critical eigenvalue(s)
has critical eigenvalue(s)  , that is,
, that is,  , and the arguments of the rest eigenvalues in absolute values are greater than
, and the arguments of the rest eigenvalues in absolute values are greater than 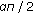 , then system (3.1) is not stable provided that
, then system (3.1) is not stable provided that 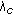 has different geometric and algebraic multiplicities.
has different geometric and algebraic multiplicities.
3.2. The Caputo Derivative Case
Now, we consider the fractional differential system with Caputo derivative

under the initial conditions

where  ,
,  , and
, and  are as in Section 3.1. Then, one can get the following theorem.
are as in Section 3.1. Then, one can get the following theorem.
Theorem 3.3.
The autonomous fractional differential system (3.17) with Caputo derivative and initial conditions (3.18) is asymptotically stable iff  . In this case, the components of the state decay towards 0 like
. In this case, the components of the state decay towards 0 like  . Moreover, the system (3.17) is stable iff either it is asymptotically stable, or those critical eigenvalues which satisfy
. Moreover, the system (3.17) is stable iff either it is asymptotically stable, or those critical eigenvalues which satisfy  have the same algebraic and geometric multiplicities.
have the same algebraic and geometric multiplicities.
Proof.
This theorem can be proved in the same manner as that in the proof of Theorem 3.1, so it is omitted here.
4. Stability of Nonautonomous Linear Fractional Differential Systems
4.1. The Riemann-Liouville Derivative Case
We will consider a nonautonomous fractional differential system with Riemann-Liouville derivative

under the initial conditions

where  , matrix
, matrix  ,
,  is a continuous matrix, and
is a continuous matrix, and  . The main results of this subsection are derived as follows.
. The main results of this subsection are derived as follows.
Theorem 4.1.
If the matrix  such that
such that  , the critical eigenvalues which satisfy
, the critical eigenvalues which satisfy  have the same algebraic and geometric multiplicities, and
have the same algebraic and geometric multiplicities, and  is bounded, then the zero solution of (4.1) is stable.
is bounded, then the zero solution of (4.1) is stable.
Proof.
Applying the Laplace transform, we can get the solution of (4.1)-(4.2),

From the proof of Theorem 3.1, the matrix  is bounded for
is bounded for  . Therefore, there exist positive numbers
. Therefore, there exist positive numbers  , such that
, such that  (
( ). Now, we can get the estimate of solution
). Now, we can get the estimate of solution 

Applying the Gronwall inequality (2.17) leads to

Thus, we derive that  is bounded according to the condition
is bounded according to the condition  , that is, the zero solution of (4.1) is stable. The proof is completed.
, that is, the zero solution of (4.1) is stable. The proof is completed.
Similarly, we can derive the following conclusion.
Theorem 4.2.
If the matrix  such that
such that  ,
,  , and
, and  (
( ,
,  ) for
) for  , then the zero solution of (4.1) is asymptotically stable.
, then the zero solution of (4.1) is asymptotically stable.
Proof.
From the proof of Theorem 3.1, the following expression is valid:

where  such that
such that  and
and  . Moreover, from (4.4) and (2.17), one has
. Moreover, from (4.4) and (2.17), one has

Substituting (4.7) into (4.6), we have

where  . It follows from the condition
. It follows from the condition  (
( ,
,  ) for
) for  that there exists a constant
that there exists a constant  , such that
, such that  and
and

So, the zero solution of (4.1) is asymptotically stable.
4.2. The Caputo Derivative Case
In this subsection, we consider a nonautonomous fractional differential system with Caputo derivative

under the initial conditions

where  ,
,  , and
, and  are as in Section 4.1,
are as in Section 4.1,  is a continuously differentiable matrix. We can get the solution of (4.10)-(4.11) by using the Laplace transform and Laplace inverse transform
is a continuously differentiable matrix. We can get the solution of (4.10)-(4.11) by using the Laplace transform and Laplace inverse transform

The main stability results of this subsection are derived as follows.
Theorem 4.3.
If the matrix  such that
such that  ,
,  , the critical eigenvalues which satisfy
, the critical eigenvalues which satisfy  have the same algebraic and geometric multiplicities, and
have the same algebraic and geometric multiplicities, and  is bounded, then the zero solution of (4.10) is stable.
is bounded, then the zero solution of (4.10) is stable.
Proof.
The proof line is similar to that of Theorem 4.1.
Theorem 4.4.
If the matrix  such that
such that  ,
,  , and
, and  (
( ,
,  ) for
) for  , then the zero solution of (4.10) is asymptotically stable.
, then the zero solution of (4.10) is asymptotically stable.
Proof.
From the solution (4.12) and Lemma 2.7, we can directly get

where  and
and  , such that
, such that  . Furthermore, there exists a constant
. Furthermore, there exists a constant  such that
such that

that is,

Substituting (4.15) into (4.13) gives

It follows from the condition  (
( ,
,  ) for
) for  that there exists a constant
that there exists a constant  , such that
, such that  and
and

So, the zero solution of (4.10) is asymptotically stable.
5. Stability of the Perturbed Systems
In this section, we only study the perturbed system of a linear fractional differential system with Riemann-Liouville derivative

under the initial conditions

where  , matrix
, matrix  , and
, and  .
.  is a continuous function in which
is a continuous function in which  ; moreover,
; moreover,  fulfils the Lipschitz condition with respect to
fulfils the Lipschitz condition with respect to  . Then, the unique solution of (5.1)-(5.2) can be written as
. Then, the unique solution of (5.1)-(5.2) can be written as

The following theorem can be proved by the same argument used in the proof of Theorem 4.1.
Theorem 5.1.
If the matrix  such that
such that  ,
,  , the critical eigenvalues which satisfy
, the critical eigenvalues which satisfy  have the same algebraic and geometric multiplicities. Moreover, suppose that there exists a positive function
have the same algebraic and geometric multiplicities. Moreover, suppose that there exists a positive function  which satisfies the following conditions:
which satisfies the following conditions:
(i) is bounded,
is bounded,
(ii) ,
,
then the zero solution of (5.1) is stable.
Theorem 5.2.
If the matrix  such that
such that  ,
,  ,
,  , and suppose that the function
, and suppose that the function  satisfies uniformly
satisfies uniformly

then the zero solution of (5.1) is asymptotically stable.
Proof.
According to the proof of Theorem 3.1 and Lemma 2.7, we have

where  such that
such that  and
and  . Taking into account the condition (5.4), there exists a constant
. Taking into account the condition (5.4), there exists a constant  , such that
, such that

Then,

where  . Applying the Gronwall inequality (2.16) to (5.7) yields
. Applying the Gronwall inequality (2.16) to (5.7) yields

So, the zero solution of (5.1) is asymptotically stable due to  . The proof is thus finished.
. The proof is thus finished.
6. Conclusion
It is well know that many physical phenomena having memory and genetic characteristics can be described by using the fractional differential systems. Especially, the fractional differential systems with order  have recently gained an increasing attention [23, 28–31]. It should be noted that [29, 30] are earlier and interesting work on fractional interval systems. Motivated by the above research activities, in this paper, we have studied the stability of linear fractional differential systems and the corresponding perturbed systems with Rimann-Liouville derivative and Caputo derivative for the commensurate order
have recently gained an increasing attention [23, 28–31]. It should be noted that [29, 30] are earlier and interesting work on fractional interval systems. Motivated by the above research activities, in this paper, we have studied the stability of linear fractional differential systems and the corresponding perturbed systems with Rimann-Liouville derivative and Caputo derivative for the commensurate order  . The main analytic tools used in this paper are the Mittag-Leffler function and the Gronwall inequality. For the autonomous linear fractional differential systems with order
. The main analytic tools used in this paper are the Mittag-Leffler function and the Gronwall inequality. For the autonomous linear fractional differential systems with order  , the necessary and sufficient conditions on stability and asymptotic stability are given, which are almost the same as those with the fractional derivative order
, the necessary and sufficient conditions on stability and asymptotic stability are given, which are almost the same as those with the fractional derivative order  . But the components of the state decay towards 0 like
. But the components of the state decay towards 0 like  , which is different from the case with Caputo derivative order
, which is different from the case with Caputo derivative order  . For the nonautonomous linear fractional differential systems, we have derived some sufficient conditions on stability and asymptotic stability. We have further given the asymptotic stability results of the perturbed systems with order
. For the nonautonomous linear fractional differential systems, we have derived some sufficient conditions on stability and asymptotic stability. We have further given the asymptotic stability results of the perturbed systems with order  .
.
References
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Gordon and Breach Science Publishers, Yverdon, Switzerland; 1993:xxxvi+976.
Debnath L: A brief historical introduction to fractional calculus. International Journal of Mathematical Education in Science and Technology 2004,35(4):487–501. 10.1080/00207390410001686571
Ross B: A brief history and exposition of the fundamental theory of fractional calculus. Lecture Notes in Mathematics 1975, 457: 1–36. 10.1007/BFb0067096
Koeller RC: Applications of fractional calculus to the theory of viscoelasticity. Journal of Applied Mechanics 1984,51(2):299–307. 10.1115/1.3167616
Sun HH, Abdelwahab AA, Onaral B: Linear approximation of transfer function with a pole of fractional power. IEEE Transactions on Automatic Control 1984,29(5):441–444. 10.1109/TAC.1984.1103551
Sun HH, Onaral B, Tsao YY: Application of the positive reality principle to metal electrode linear polarization phenomena. IEEE Transactions on Biomedical Engineering 1984,31(10):664–674.
Heaviside O: Electromagnetic Theory. Chelsea, New York, NY, USA; 1971.
Tavazoei MS, Haeri M: A note on the stability of fractional order systems. Mathematics and Computers in Simulation 2009,79(5):1566–1576. 10.1016/j.matcom.2008.07.003
Matignon D: Stability results for fractional differential equations with applications to control processing. Proceedings of the IMACS-SMC, 1996 2: 963–968.
Malti R, Cois O, Aoun M, Levron F, Oustaloup A: Computing impulse response energy of fractional transfer function. Proceedings of the 15th IFAC World Congress, 2002, Barcelona, Spain
Moze M, Sabatier J, Oustaloup A: LMI characterization of fractional systems stability. In Advances in Fractional Calculus. Edited by: Sabatier J, Agrawal OP, Tenreiro Machado JA. Springer, Dordrecht, The Netherlands; 2007:419–434.
Deng W, Li C, Lü J: Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dynamics 2007,48(4):409–416. 10.1007/s11071-006-9094-0
Odibat ZM: Analytic study on linear systems of fractional differential equations. Computers & Mathematics with Applications 2010,59(3):1171–1183.
Radwan AG, Soliman AM, Elwakil AS, Sedeek A: On the stability of linear systems with fractional-order elements. Chaos, Solitons and Fractals 2009,40(5):2317–2328. 10.1016/j.chaos.2007.10.033
Sabatier J, Moze M, Farges C: LMI stability conditions for fractional order systems. Computers & Mathematics with Applications 2010,59(5):1594–1609. 10.1016/j.camwa.2009.08.003
Qian D, Li C, Agarwal RP, Wong PJY: Stability analysis of fractional differential system with Riemann-Liouville derivative. Mathematical and Computer Modelling 2010,52(5–6):862–874. 10.1016/j.mcm.2010.05.016
Li CP, Zhang FR: A survey on thestability of fractional differential equations. The European Physical Journal Special Topics 2011, 193: 27–47. 10.1140/epjst/e2011-01379-1
Matignon D: Reprsentations en variables d'tat demodles de guides d'ondes avec derivation fractionnaire, Thèse de Doctorat. Université Paris-Sud 11; 1994.
Li CP, Zhao ZG: Numerical approximation of nonlinear fractional differential equuations with subdiffusion and Ssperdiffusion. Computers and Mathematics with Applications. In press
Li CP, Gong ZG, Qian DL, Chen YQ: On the bound of the Lyapunov exponents for the fractional differential systems. Chaos 2010,20(1, article 013127):7.
Li C, Xia X: On the bound of the Lyapunov exponents for continuous systems. Chaos 2004,14(3):557–561. 10.1063/1.1768911
Li CP, Chen G: Estimating the Lyapunov exponents of discrete systems. Chaos 2004,14(2):343–346. 10.1063/1.1741751
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science, Amsterdam, The Netherlands; 2006:xvi+523.
Wen X-J, Wu Z-M, Lu J-G: Stability analysis of a class of nonlinear fractional-order systems. IEEE Transactions on Circuits and Systems II 2008,55(11):1178–1182.
Zhang FZ: Matrix Theory, Universitext. Springer, New York, NY, USA; 1999:xiv+277.
Corduneanu C: Principles of Differential and Integral Equations. Allyn and Bacon, Boston, Mass, USA; 1971:vi+201.
Sun Z-Z, Wu XN: A fully discrete difference scheme for a diffusion-wave system. Applied Numerical Mathematics 2006,56(2):193–209. 10.1016/j.apnum.2005.03.003
Ahn H-S, Chen YQ, Podlubny I: Robust stability test of a class of linear time-invariant interval fractional-order system using Lyapunov inequality. Applied Mathematics and Computation 2007,187(1):27–34. 10.1016/j.amc.2006.08.099
Ahn H-S, Chen YQ: Necessary and sufficient stability condition of fractional-order interval linear systems. Automatica 2008,44(11):2985–2988. 10.1016/j.automatica.2008.07.003
Luchko YF, Rivero M, Trujillo JJ, Velasco MP: Fractional models, non-locality, and complex systems. Computers & Mathematics with Applications 2010,59(3):1048–1056.
Acknowledgments
The authors wish to thank Professors D. Baleanu and Juan J. Trujillo for their kind invitation to submit our paper to their special issue on Fractional Models and their Applications. They also thank the anonymous reviewers of this paper for their careful reading and invaluable correction suggestions. The present work was partially supported by the National Natural Science Foundation of China under Grant no. 10872119 and the the Key Disciplines of Shanghai Municipality under Grant no. S30104.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, F., Li, C. Stability Analysis of Fractional Differential Systems with Order Lying in (1, 2). Adv Differ Equ 2011, 213485 (2011). https://doi.org/10.1155/2011/213485
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/213485
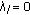 , then
, then 
 , three cases will be considered separately.
, three cases will be considered separately.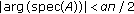 , then system (3.1) is not stable.
, then system (3.1) is not stable.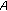 has zero eigenvalue, system (3.1) is not stable.
has zero eigenvalue, system (3.1) is not stable. has critical eigenvalue(s)
has critical eigenvalue(s)  , that is,
, that is,  , and the arguments of the rest eigenvalues in absolute values are greater than
, and the arguments of the rest eigenvalues in absolute values are greater than 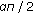 , then system (3.1) is not stable provided that
, then system (3.1) is not stable provided that 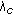 has different geometric and algebraic multiplicities.
has different geometric and algebraic multiplicities.