- Research Article
- Open access
- Published:
On a Nonlinear Integral Equation with Contractive Perturbation
Advances in Difference Equations volume 2011, Article number: 154742 (2011)
Abstract
We get an existence result for solutions to a nonlinear integral equation with contractive perturbation by means of Krasnoselskii's fixed point theorem and especially the theory of measure of weak noncompactness.
1. Introduction
The integral equations have many applications in mechanics, physics, engineering, biology, economics, and so on. It is worthwhile mentioning that some problems considered in the theory of abstract differential equations also lead us to integral equations in Banach space, and some foundational work has been done in [1–8].
In this paper we want to study the following integral equation:

in the Banach space  .
.
This equation has been studied when  in [9] with
in [9] with  and [10] with a perturbation term
and [10] with a perturbation term  . Our paper extends their work to more general spaces and some modifications are also given on an error of [10].
. Our paper extends their work to more general spaces and some modifications are also given on an error of [10].
Our paper is organized as follows.
In Section 2, some notations and auxiliary results will be given. We will introduce the main tools measure of weak noncompactness and Krasnoselskii's fixed point theorem in Section 3 and Section 4. The main theorem in our paper will be established in Section 5.
2. Preliminaries
First of all, we give out some notations to appear in the following.
 denotes the set of real numbers and
denotes the set of real numbers and  . Suppose that
. Suppose that  is a separable locally compact Banach space with norm
is a separable locally compact Banach space with norm  in the whole paper. (Remark: the locally compactness of
in the whole paper. (Remark: the locally compactness of  will be used in Lemma 2.2). Let
will be used in Lemma 2.2). Let  be a Lebesgue measurable subset of
be a Lebesgue measurable subset of  and
and  denote the Lebesgue measure of
denote the Lebesgue measure of  .
.
Let  denote the space of all real Lebesgue measurable functions defined on
denote the space of all real Lebesgue measurable functions defined on  to
to  .
.  forms a Banach space under the norm
forms a Banach space under the norm

for  .
.
Definition 2.1.
A function  is said to satisfy Carathéodory conditions if
is said to satisfy Carathéodory conditions if
-
(i)
 is measurable in
is measurable in  for any
for any 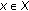 ;
; -
(ii)
 is continuous in
is continuous in  for almost all
for almost all  .
.
The following lemma which we will use in the proof of our main theorem explains the structure of functions satisfying Carathéodory conditions with the assumption that the space  is separable and locally compact (see [11]).
is separable and locally compact (see [11]).
Lemma 2.2.
Let  be a bounded interval and
be a bounded interval and  be a functionsatisfying Carathéodory conditions. Then it possesses the Scorza-Dragoni property. That is each
be a functionsatisfying Carathéodory conditions. Then it possesses the Scorza-Dragoni property. That is each  , there exists a closed subset
, there exists a closed subset  of
of  such that
such that  and
and  is continuous.
is continuous.
The operator  is called superposition operator or Nemytskij operator associated to
is called superposition operator or Nemytskij operator associated to  . The following lemma on superposition operator is important in our theorem (see [12] and also in [13]).
. The following lemma on superposition operator is important in our theorem (see [12] and also in [13]).
Lemma 2.3.
The superposition operator  generated by the function
generated by the function  maps continuously the space
maps continuously the space  into itself (
into itself ( may be unbounded interval) if and only if there exist
may be unbounded interval) if and only if there exist  and a nonnegative constant
and a nonnegative constant  such that
such that

for all  and
and  .
.
The Volterra operator which is defined by  for
for  where
where  is measurable with respect to both variables. If
is measurable with respect to both variables. If  transforms
transforms  into itself it is then a bounded operator with norm
into itself it is then a bounded operator with norm  which is majorized by the number
which is majorized by the number

3. Measure of Weak Noncompactness
In this section we will recall the concept of measure of weak noncompactness which is the key point to complete our proof of main theorem in Section 5.
Let  be a Banach space.
be a Banach space.  and
and  denote the collections of all nonempty bounded subsets and relatively weak compact subsets, respectively.
denote the collections of all nonempty bounded subsets and relatively weak compact subsets, respectively.
Definition 3.1.
A function  is said to be a measure of weak noncompactness if it satisfies the following conditions:
is said to be a measure of weak noncompactness if it satisfies the following conditions:
-
(1)
the family Ker
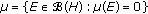 is nonempty and Ker
is nonempty and Ker 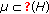 ;
; -
(2)
if
 , we have
, we have  ;
; -
(3)
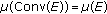 , where
, where  denotes the convex closed hull of
denotes the convex closed hull of  ;
; -
(4)
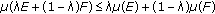 for
for  ;
; -
(5)
If
 is a decreasing sequence, that is,
is a decreasing sequence, that is,  , every
, every 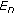 is weakly closed,
is weakly closed,and
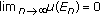 , then
, then 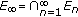 is nonempty.
is nonempty.
From [14], we see the following measure of weak noncompact:

where  denotes the closed ball in
denotes the closed ball in  centered at 0 with radius
centered at 0 with radius  .
.
In [15], Appel and De Pascale gave to  the following simple form in
the following simple form in  space:
space:

for a nonempty and bounded subset  of space
of space  .
.
Let

for a nonempty and bounded subset  of space
of space  .
.
It is easy to know that  is a measure of weak noncompactness in space
is a measure of weak noncompactness in space  following the verification in [16].
following the verification in [16].
4. Krasnoselskii's Fixed Point Theorem
The following is the Krasnoselskii's fixed point theorem which will be utilized to obtain the existence of solutions in the next section.
Theorem 4.1.
Let  be a closed convex and nonempty subset of a Banach space
be a closed convex and nonempty subset of a Banach space  . Let
. Let  be two operators such that
be two operators such that
-
(i)
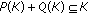 ;
; -
(ii)
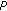 is a contraction mapping;
is a contraction mapping; -
(iii)
 is relatively compact and
is relatively compact and 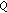 is continuous.
is continuous.
Then there exists  such that
such that  .
.
Remark 4.2.
In [9], they proved the existence of solutions by means of Schauder fixed point theorem. With the presence of the Perturbation term  in the integral equation, the Schauder fixed point theorem is invalid. To overcome this difficulty we will use the Kransnoselskii's fixed point theorem to obtain the existence of solutions.
in the integral equation, the Schauder fixed point theorem is invalid. To overcome this difficulty we will use the Kransnoselskii's fixed point theorem to obtain the existence of solutions.
Remark 4.3.
We will see in the following section that the important step is the construction of  by means of measure of weak noncompactness. This is the biggest difference between our paper from [10].
by means of measure of weak noncompactness. This is the biggest difference between our paper from [10].
Remark 4.4.
The Krasnoselskii's fixed point theorem was extended to general case in [17] (see also in [13]). In [10], they used the general Krasnoselskii's fixed point theorem to obtain the existence result. It can be seen in the next section of our paper that the classical Krasnoselskii's fixed point theorem is enough unless we need more general conditions on the perturbation term  .
.
5. Main Theorem and Proof
Our main theorem in this paper is stated as follows.
Theorem 5.1.
Suppose that the following assumptions are satisfied.
(H1) The functions  satisfy Carathéodory conditions, and there exist constants
satisfy Carathéodory conditions, and there exist constants  and functions
and functions  such that
such that

for  and
and 
 .
.
(H2) Then function  satisfies Carathéodory conditons, and the linear Volterra integral operator
satisfies Carathéodory conditons, and the linear Volterra integral operator  defined by
defined by

transforms the space  into itself.
into itself.
(H3) The function  is measurable in t and continuous in x and y for almost all t. And there exist two positive constants
is measurable in t and continuous in x and y for almost all t. And there exist two positive constants  and a function
and a function  such that
such that

for  and
and  . Additionally, the function
. Additionally, the function  satisfies the following Lipschitz condition for almost all
satisfies the following Lipschitz condition for almost all  :
:

(H4) The function  such that
such that  where
where  is an arbitrary subset of
is an arbitrary subset of  , and
, and  is bounded by
is bounded by  for all
for all  .
.
(H5)  , where
, where denotes the norm of the linear Volterra operator
denotes the norm of the linear Volterra operator  .
.
(H6)  .
.
Then the integral equation (1.1) has at least one solution  .
.
Proof.
Equation (1.1) may be written in the following form:

where  is the linear Volterra integraloperator and
is the linear Volterra integraloperator and  is the superposition operator generated by the function
is the superposition operator generated by the function  .
.
The proof will be given in six steps.
Step 1.
There exists  such that
such that  , where
, where  is a ball centered zero element with radius
is a ball centered zero element with radius  in
in  .
.
Let  and
and  be arbitrary functions in
be arbitrary functions in  with
with  to be determined later. In view of our assumptions we get
to be determined later. In view of our assumptions we get

We then derive that  by taking
by taking

where  by assumption (H5).
by assumption (H5).
Step 2.
 for allbounded subset
for allbounded subset  of
of  .
.
Take a arbitrary numbers  and
and  such that
such that  .
.
For any  , we have
, we have

It follows that  by definition (3.2).
by definition (3.2).
For  and any
and any  , we have
, we have

and then  by definition (3.3).
by definition (3.3).
From above, we then obtain  for all bounded subset
for all bounded subset  of
of  .
.
Step 3.
We will construct a nonempty closed convex weakly compact set in on which we will apply fixed point theorem to prove the existence of solutions.
Let  where
where  is defined in Step 1,
is defined in Step 1,  and so on. We then get a decreasing sequence
and so on. We then get a decreasing sequence  , that is,
, that is,  for
for  . Obviously all sets belonging to this sequence are closed and convex, so weakly closed. By the fact proved in Step 2 that
. Obviously all sets belonging to this sequence are closed and convex, so weakly closed. By the fact proved in Step 2 that  for all bounded subset
for all bounded subset  of
of  , we have
, we have

which yields that  .
.
Denote  , and then
, and then  . By the definition of measure of weak noncompact we know that
. By the definition of measure of weak noncompact we know that  is nonempty. Moreover,
is nonempty. Moreover,  .
.
 is just nonempty closed convex weakly compact set which we need in the following steps.
is just nonempty closed convex weakly compact set which we need in the following steps.
Step 4.
 is relatively compact in
is relatively compact in  , where
, where  is just the set constructed in Step 3.
is just the set constructed in Step 3.
Let  be arbitrary sequence. Since
be arbitrary sequence. Since  ,
,  ,
,  , the following inequality is satisfied:
, the following inequality is satisfied:

Considering the function  on
on  and
and  on
on  , we can find a closed subset
, we can find a closed subset  of interval
of interval  , such that
, such that  , and such that
, and such that  and
and  is continuous. Especially
is continuous. Especially  is uniformly continuous.
is uniformly continuous.
Let us take arbitrarily  and assume
and assume  without loss of generality. For an arbitrary fixed
without loss of generality. For an arbitrary fixed  and denoting
and denoting  we obtain:
we obtain:

where  denotes the modulusof continuity of the function
denotes the modulusof continuity of the function  on the set
on the set  and
and  . The last inequality of (5.12) is obtained since
. The last inequality of (5.12) is obtained since  , where
, where  is just the one in the Step 1.
is just the one in the Step 1.
Taking into account the fact that the  , we infer that the terms of the numerical sequence
, we infer that the terms of the numerical sequence  are arbitrarily small provided that the number
are arbitrarily small provided that the number  is small enough.
is small enough.
Since  is also arbitrarily small provided that the number
is also arbitrarily small provided that the number  is small enough, the right of (5.12) then tends to zero independent of
is small enough, the right of (5.12) then tends to zero independent of  as
as  tends to zero. We then have
tends to zero. We then have  is equicontinuous in the space
is equicontinuous in the space  .
.
On the other hand,

From above, we then obtain that  is equibounded in the space
is equibounded in the space  .
.
By assumption (H1),we have the operator  is continuous. So
is continuous. So  forms a relatively compact set in the space
forms a relatively compact set in the space  .
.
Further observe that the above result does not depend on the choice of  . Thus we can construct a sequence
. Thus we can construct a sequence  of closed subsets of the interval
of closed subsets of the interval  such that
such that  as
as  and such that the sequence
and such that the sequence  is relatively compact in every space
is relatively compact in every space  . Passing to subsequence if necessary we can assume that
. Passing to subsequence if necessary we can assume that  is a cauchy sequence in each space
is a cauchy sequence in each space  .
.
Observe the fact  , then
, then  . By the definition (3.2), let us choose a number
. By the definition (3.2), let us choose a number  such that for each closed subset
such that for each closed subset  of the interval
of the interval  provided that
provided that  we have
we have

for any  , where
, where  .
.
By the fact that  is a cauchy sequence in each space
is a cauchy sequence in each space  , we can choose a natural number
, we can choose a natural number  such that
such that  and
and  , and for arbitrary natural number
, and for arbitrary natural number  the following inequality holds:
the following inequality holds:

for any  .
.
Combining (5.11), (5.14) and (5.15), we get

which means that  is a cauchy sequence in the space
is a cauchy sequence in the space  . Hence we conclude that
. Hence we conclude that  is relatively compact in
is relatively compact in  .
.
Step 5.
The operator  is a contraction mapping:
is a contraction mapping:

where we have made a transformation  in the above process. Since
in the above process. Since  by assumption (H6), we then get the fact that the operator
by assumption (H6), we then get the fact that the operator  is a contraction mapping.
is a contraction mapping.
Step 6.
We now check out that the conditions needed in Krasnoselskii's fixed point theorem are fulfilled.
-
(1)
From Step 3, we know that
 , where
, where 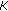 is the set constructed in Step 3.
is the set constructed in Step 3. -
(2)
From Step 5, we know that
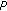 is a contraction mapping.
is a contraction mapping. -
(3)
From the Step 4 and assumptions (H1), (H2),
 is relatively compact and
is relatively compact and  is continuous.
is continuous.
We apply Theorem 4.1, and then obtain that (1.1) has at least one solution in  .
.
Remark 5.2.
When  , in [10] they said
, in [10] they said  is weakly sequence compact in their Step 1 of main proof. From our proof, we know that their proof is not precise, since in Step 4, one of the crucial conditions to prove the relatively compactness of
is weakly sequence compact in their Step 1 of main proof. From our proof, we know that their proof is not precise, since in Step 4, one of the crucial conditions to prove the relatively compactness of  is that
is that  is weakly compact. We can only obtain that
is weakly compact. We can only obtain that  is weakly sequence compact as a mapping from
is weakly sequence compact as a mapping from  to
to  which is the weakly compact set defined in Step 3. The construction of set
which is the weakly compact set defined in Step 3. The construction of set  overcomes the fault in [10], and we obtain the existence result finally.
overcomes the fault in [10], and we obtain the existence result finally.
References
Liang J, Liu JH, Xiao T-J: Nonlocal problems for integrodifferential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(6):815-824.
Liang J, Xiao T-J: Semilinear integrodifferential equations with nonlocal initial conditions. Computers & Mathematics with Applications 2004,47(6-7):863-875. 10.1016/S0898-1221(04)90071-5
Liang J, Zhang J, Xiao T-J: Composition of pseudo almost automorphic and asymptotically almost automorphic functions. Journal of Mathematical Analysis and Applications 2008,340(2):1493-1499. 10.1016/j.jmaa.2007.09.065
Xiao T-J, Liang J: Approximations of Laplace transforms and integrated semigroups. Journal of Functional Analysis 2000,172(1):202-220. 10.1006/jfan.1999.3545
Xiao T-J, Liang J: Existence of classical solutions to nonautonomous nonlocal parabolic problems. Nonlinear Analysis, Theory, Methods and Applications 2005,63(5–7):e225-e232.
Xiao T-J, Liang J: Blow-up and global existence of solutions to integral equations with infinite delay in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,71(12):e1442-e1447. 10.1016/j.na.2009.01.204
Xiao T-J, Liang J, van Casteren J: Time dependent Desch-Schappacher type perturbations of Volterra integral equations. Integral Equations and Operator Theory 2002,44(4):494-506. 10.1007/BF01193674
Xiao T-J, Liang J, Zhang J: Pseudo almost automorphic solutions to semilinear differential equations in Banach spaces. Semigroup Forum 2008,76(3):518-524. 10.1007/s00233-007-9011-y
Banaś J, Chlebowicz A: On existence of integrable solutions of a functional integral equation under Carathéodory conditions. Nonlinear Analysis. Theory, Methods & Applications 2009,70(9):3172-3179. 10.1016/j.na.2008.04.020
Taoudi MA: Integrable solutions of a nonlinear functional integral equation on an unbounded interval. Nonlinear Analysis. Theory, Methods & Applications 2009,71(9):4131-4136. 10.1016/j.na.2009.02.072
Ricceri B, Villani A: Separability and Scorza-Dragoni's property. Le Matematiche 1982,37(1):156-161.
Lucchetti R, Patrone F: On Nemytskii's operator and its application to the lower semicontinuity of integral functionals. Indiana University Mathematics Journal 1980,29(5):703-713. 10.1512/iumj.1980.29.29051
Djebali S, Sahnoun Z:Nonlinear alternatives of Schauder and Krasnosel'skij types with applications to Hammerstein integral equations in
 spaces. Journal of Differential Equations 2010,249(9):2061-2075. 10.1016/j.jde.2010.07.013
spaces. Journal of Differential Equations 2010,249(9):2061-2075. 10.1016/j.jde.2010.07.013De Blasi FS: On a property of the unit sphere in Banach spaces. Bulletin Mathématique de la Société des Sciences Mathématiques de Roumanie 1997, 21: 259-262.
Appel J, De Pascale E: Su alcuni parametri connessi con la misura di non compatteza di Hausdorff in spazi di funzioni misurabilli. Bollettino della Unione Matematica Italiana. B 1984,3(6):497-515.
Banaś J, Knap Z: Measures of weak noncompactness and nonlinear integral equations of convolution type. Journal of Mathematical Analysis and Applications 1990,146(2):353-362. 10.1016/0022-247X(90)90307-2
Latrach K, Taoudi MA:Existence results for a generalized nonlinear Hammerstein equation on
 spaces. Nonlinear Analysis. Theory, Methods & Applications 2007,66(10):2325-2333. 10.1016/j.na.2006.03.022
spaces. Nonlinear Analysis. Theory, Methods & Applications 2007,66(10):2325-2333. 10.1016/j.na.2006.03.022
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, H. On a Nonlinear Integral Equation with Contractive Perturbation. Adv Differ Equ 2011, 154742 (2011). https://doi.org/10.1155/2011/154742
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/154742
 is measurable in
is measurable in  for any
for any 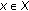 ;
; is continuous in
is continuous in  for almost all
for almost all  .
.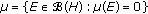 is nonempty and Ker
is nonempty and Ker 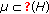 ;
; , we have
, we have  ;
;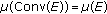 , where
, where  denotes the convex closed hull of
denotes the convex closed hull of  ;
;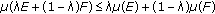 for
for  ;
; is a decreasing sequence, that is,
is a decreasing sequence, that is,  , every
, every 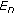 is weakly closed,
is weakly closed,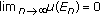 , then
, then 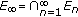 is nonempty.
is nonempty.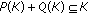 ;
;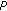 is a contraction mapping;
is a contraction mapping; is relatively compact and
is relatively compact and  is continuous.
is continuous. , where
, where 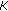 is the set constructed in Step 3.
is the set constructed in Step 3.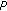 is a contraction mapping.
is a contraction mapping. is relatively compact and
is relatively compact and  is continuous.
is continuous. spaces. Journal of Differential Equations 2010,249(9):2061-2075. 10.1016/j.jde.2010.07.013
spaces. Journal of Differential Equations 2010,249(9):2061-2075. 10.1016/j.jde.2010.07.013 spaces. Nonlinear Analysis. Theory, Methods & Applications 2007,66(10):2325-2333. 10.1016/j.na.2006.03.022
spaces. Nonlinear Analysis. Theory, Methods & Applications 2007,66(10):2325-2333. 10.1016/j.na.2006.03.022