- Research Article
- Open access
- Published:
On Linear Combinations of Two Orthogonal Polynomial Sequences on the Unit Circle
Advances in Difference Equations volume 2010, Article number: 406231 (2010)
Abstract
Let  be a monic orthogonal polynomial sequence on the unit circle. We define recursively a new sequence
be a monic orthogonal polynomial sequence on the unit circle. We define recursively a new sequence  of polynomials by the following linear combination:
of polynomials by the following linear combination:  ,
,  ,
,  . In this paper, we give necessary and sufficient conditions in order to make
. In this paper, we give necessary and sufficient conditions in order to make  be an orthogonal polynomial sequence too. Moreover, we obtain an explicit representation for the Verblunsky coefficients
be an orthogonal polynomial sequence too. Moreover, we obtain an explicit representation for the Verblunsky coefficients  and
and  in terms of
in terms of  and
and  . Finally, we show the relation between their corresponding Carathéodory functions and their associated linear functionals.
. Finally, we show the relation between their corresponding Carathéodory functions and their associated linear functionals.
1. Notation and Preliminary Results
We recall some definitions and general results about orthogonal polynomials on the unit circle (OPUC). They can be seen in [1–3].
Along this paper, we will use the following notations. We denote by  the linear space of Laurent polynomials with complex coefficients and by
the linear space of Laurent polynomials with complex coefficients and by  the dual algebraic space of
the dual algebraic space of  . Let
. Let  be the space of complex polynomials.
be the space of complex polynomials.
Definition 1.1.
Let  . Denoting by
. Denoting by  ,
,  , we say that
, we say that
-
(i)
 is Hermitian if
is Hermitian if  ,
,  ;
; -
(ii)
 is regular or quasidefinite (positive definite) if the principal minors of the moment matrix are nonsingular (positive), that is,
is regular or quasidefinite (positive definite) if the principal minors of the moment matrix are nonsingular (positive), that is, (1.1)
(1.1)
In any case we denote  ,
,  with
with  .
.
The sequence  is said to be the sequence of the moments associated with
is said to be the sequence of the moments associated with  .
.
Furthermore, if  is a positive definite linear functional then a finite nontrivial positive Borel measure
is a positive definite linear functional then a finite nontrivial positive Borel measure  supported on the unit circle exists such that
supported on the unit circle exists such that

Definition 1.2.
Let  be a complex polynomial sequence with
be a complex polynomial sequence with  . We say that
. We say that  is a sequence of orthogonal polynomials (OPSs) with respect to the linear and Hermitian functional
is a sequence of orthogonal polynomials (OPSs) with respect to the linear and Hermitian functional  if
if

In the sequel, we denote by  the monic orthogonal polynomial sequence (MOPS) associated with
the monic orthogonal polynomial sequence (MOPS) associated with  .
.
For simplicity, along this paper we also assume that  is normalized (i.e.,
is normalized (i.e.,  ). It is well known that the regularity of
). It is well known that the regularity of  is a necessary and sufficient condition for the existence of a sequence of orthogonal polynomials on the unit circle. On the other hand, the polynomials
is a necessary and sufficient condition for the existence of a sequence of orthogonal polynomials on the unit circle. On the other hand, the polynomials  satisfy the so-called Szegö recurrence relations
satisfy the so-called Szegö recurrence relations




where  is the reversed polynomial of
is the reversed polynomial of  ,
,  .
.
Definition 1.3.
Given an MOPS  , the sequence of kernels of parameter
, the sequence of kernels of parameter  associated with the linear functional
associated with the linear functional  is defined by
is defined by

This sequence verifies the following properties:




To the linear functional  we can associate a formal series
we can associate a formal series  as follows:
as follows:

In the positive definite case,  is called the Carathéodory function associated with
is called the Carathéodory function associated with  . In this case,
. In this case,  can be written as
can be written as

The measure  can be reconstructed from
can be reconstructed from  by means of the inversion formula. The aim of this paper is the analysis of the following problem. Given an MOPS on the unit circle
by means of the inversion formula. The aim of this paper is the analysis of the following problem. Given an MOPS on the unit circle  , orthogonal with respect to a linear functional
, orthogonal with respect to a linear functional  , to find necessary and sufficient conditions in order to make a sequence of monic polynomials
, to find necessary and sufficient conditions in order to make a sequence of monic polynomials  defined by
defined by

an MOPS with respect to a linear functional  . Further more, to find the relation between the linear functionals
. Further more, to find the relation between the linear functionals  and
and  and their corresponding Carathéodory functions.
and their corresponding Carathéodory functions.
Many authors have dealt with this kind of problems. In the constructive theory of orthogonal polynomials they have been called inverse problems. Concretely, an inverse problem for linear functionals can be stated as follows. Given two sequences of monic polynomials  and
and  , to find necessary and sufficient conditions in order to make
, to find necessary and sufficient conditions in order to make  an MOPS when
an MOPS when  is a MOPS and they are related by
is a MOPS and they are related by

where  and
and  are fixed functions. As a next step, to find the relation between the functionals.
are fixed functions. As a next step, to find the relation between the functionals.
For instance, this subject has been treated in [4–6] in the context of the theory of orthogonal polynomials on the real line. For orthogonal polynomials with respect to measures supported on the unit circle, in [7] there have been relevant results.
The structure of this paper is the following. In Section 2 we give the necessary conditions in order to be sure that the problem (1.15) admits a nontrivial solution. In Section 3, we prove a sufficient condition and we obtain the explicit solution in terms of  and
and  . Section 4 is devoted to find the functional relation between
. Section 4 is devoted to find the functional relation between  and
and  . Finally, Section 5 contains the rational relation between the corresponding Carathéodory functions.
. Finally, Section 5 contains the rational relation between the corresponding Carathéodory functions.
2. Necessary Conditions
Let  be a monic orthogonal polynomial sequence and let
be a monic orthogonal polynomial sequence and let  be a monic polynomial sequence. We assume that there exist sequences of complex numbers
be a monic polynomial sequence. We assume that there exist sequences of complex numbers  and
and  such that the following relation holds:
such that the following relation holds:

Also, we assume  and
and  and
and  , with
, with  and
and  .
.
In this section, we find some necessary conditions in order to make the sequence  defined recursively from
defined recursively from  by relation (2.1) an MOPS.
by relation (2.1) an MOPS.
With this aim, we define the complex numbers  and
and  as follows:
as follows:


The following proposition justifies this choice.
Proposition 2.1.
Let  be the monic sequence given as in (2.1). If
be the monic sequence given as in (2.1). If  is an MOPS, then the following relations hold:
is an MOPS, then the following relations hold:


Moreover,


Proof.
From (1.4) together with the definition of  (2.1), we have
(2.1), we have

Since  is a MOPS, using (1.4) we have
is a MOPS, using (1.4) we have

That is,

Using (1.4) and (1.5) in both sequences, we get

Taking  we have (2.4). Observe that, this is as same as (2.1) for
we have (2.4). Observe that, this is as same as (2.1) for  .
.
Identifying the coefficients of degree  , then (2.5) holds. Therefore, we can rewrite (2.11) as (2.6).
, then (2.5) holds. Therefore, we can rewrite (2.11) as (2.6).
On the other hand, applying the  -operator in (2.1) we have
-operator in (2.1) we have  . Substituting in (2.6) and using (2.1), we obtain (2.7).
. Substituting in (2.6) and using (2.1), we obtain (2.7).
In the sequel, we denote by  the linear regular functional associated with
the linear regular functional associated with  and by
and by  the linear regular functional associated with
the linear regular functional associated with  . Besides, we denote by
. Besides, we denote by  the real number such that
the real number such that  with
with  . Therefore,
. Therefore,  .
.
Corollary 2.2.
Under the same conditions as in Proposition 2.1, the following assertions hold:
-
(i)
If
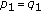 , then
, then  and
and 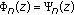 , for all
, for all  ,
, -
(ii)
If
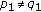 and
and 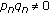 , for all
, for all  , then
, then  , for all
, for all 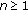 ,
, -
(iii)
Assume
 and
and  , for all
, for all 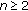 , then
, then  if and only if
if and only if 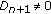 , for all
, for all  . Moreover,
. Moreover,  for all
for all  .
.
Proof.
-
(i)
We eliminate
 using equalities (2.2)–(2.4) and (2.3)–(2.5). By doing this, we get
using equalities (2.2)–(2.4) and (2.3)–(2.5). By doing this, we get  (2.12)
(2.12)
Taking  , we obtain
, we obtain  .
.
If  , then
, then  and thus
and thus  . Wherefrom
. Wherefrom  . Now, using (2.1) we have
. Now, using (2.1) we have  .
.
Proceeding in the same way for  we obtain
we obtain  , hence
, hence  and
and  , and thus successively.
, and thus successively.
-
(ii)
Assume that there exits
 such that
such that 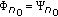 . From (2.1), written for
. From (2.1), written for 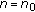 , it holds that
, it holds that  and then
and then  , and thus successively.
, and thus successively.
Hence,  , in contradiction with the hypothesis.
, in contradiction with the hypothesis.
-
(iii)
The result follows from (2.6) and the above item.
On the other hand, applying the  -operator in (2.6), we obtain
-operator in (2.6), we obtain  for
for  .
.
Remark 2.3.
The situation  is the trivial case, that is,
is the trivial case, that is,  , for all
, for all  . For this reason, in the sequel, it will be excluded.
. For this reason, in the sequel, it will be excluded.
The next result will be used later.
Lemma 2.4.
Under the same conditions as in Proposition 2.1 together with  , the following assertions hold:
, the following assertions hold:


Proof.
Using (2.1) we obtain

Since that  , then (2.13) follows.
, then (2.13) follows.
We obtain (2.14) changing  by
by  .
.
For all  such that
such that  , we define the following complex number:
, we define the following complex number:

This number plays a very important role in the solution of our problem.
Proposition 2.5.
Assume that  and
and  are two MOPSs that verify (2.1) with
are two MOPSs that verify (2.1) with  and
and  , for all
, for all  . If moreover
. If moreover  for all
for all  , then the following relation linking
, then the following relation linking  and
and  holds:
holds:

Proof.
From (2.6) and (2.7), for all  , we have the system
, we have the system

The corresponding determinant

is not null, since  together with Corollary 2.2(iii). Wherefrom, it has a unique solution for
together with Corollary 2.2(iii). Wherefrom, it has a unique solution for  .
.
By solving this, we get (2.17).
In the sequel, we denote by  the sequence of the kernels corresponding to
the sequence of the kernels corresponding to  . For the sequence
. For the sequence  we keep the same notations as in Section 1.
we keep the same notations as in Section 1.
Proposition 2.6.
Assume that  and
and  are two MOPS that verify (2.1) with
are two MOPS that verify (2.1) with  and
and  , for all
, for all  . Also assume
. Also assume  , for all
, for all  . Under these conditions, then the following assertions hold
. Under these conditions, then the following assertions hold
-
(i)
 , for all
, for all 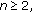
-
(ii)
There exist two complex numbers
 and
and 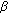 with
with 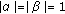 such that
such that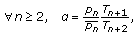 (2.20)
(2.20)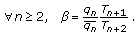 (2.21)
(2.21)Here, the initial parameters
 and
and  are given by
are given by  and
and  ,
, -
(iii)
The sequences
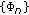 and
and 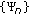 are connected by the following formulas:
are connected by the following formulas: (2.22)
(2.22) (2.23)
(2.23)
Proof.
Item (i) follows immediately from (2.17). Indeed, if we take  , we obtain
, we obtain  .
.
Let us proceed with the proof of (ii). Inserting

in (2.17), we have

Using the recurrences (1.6) and (1.7) in the right-hand side we deduce

In order to eliminate the polynomial  , we write (2.26) for
, we write (2.26) for  and we combine it with (2.17). Concretely, we multiply (2.17) by
and we combine it with (2.17). Concretely, we multiply (2.17) by  and (2.26) by
and (2.26) by  . By doing this, we obtain
. By doing this, we obtain

where

Given that  and
and  have not common roots, then
have not common roots, then  , for all
, for all  .
.
Using (2.28) we obtain

Combining these relations, we deduce

since  .
.
This complex constant is denoted in the statement by  . The property
. The property  is a consequence of Corollary 2.2(iii). On the other hand, the explicit expressions of
is a consequence of Corollary 2.2(iii). On the other hand, the explicit expressions of  and
and  follow from (2.7) for
follow from (2.7) for  and
and  , respectively.
, respectively.
This completes the proof of (ii) because the complex number  exits by the symmetry of the problem.
exits by the symmetry of the problem.
Finally, we show (iii). Using again (2.17), we have

Putting  , we get
, we get

Substituting this relation in (2.31) and using the recurrences of the kernels (1.9) and (1.10), (2.22) holds.
In order to state the converse we need the following assertions.
Proposition 2.7.
Under the hypothesis of Proposition 2.6,



Proof.
From (1.4),

Here, we use (2.31) to substitute the terms  and
and  as function of
as function of  . By doing this, we deduce
. By doing this, we deduce

Equating this formula with (2.25), previously written for  , and applying (1.4) we get
, and applying (1.4) we get

Putting  , then the independent term vanishes and the previous relation becomes
, then the independent term vanishes and the previous relation becomes

Using again the fact that  and
and  have no common roots and
have no common roots and  , it follows that the coefficients in the last relation are zero and this implies (2.33) and (2.34).
, it follows that the coefficients in the last relation are zero and this implies (2.33) and (2.34).
Let us proceed with (2.35). From (2.33) and (2.34), for all  , we have
, we have

On the other hand, substituting in  the relations (2.33) and (2.34), we obtain
the relations (2.33) and (2.34), we obtain

We can eliminate  using
using  . Moreover, multiplying by
. Moreover, multiplying by  we find
we find

Therefore,

Finally, we use (2.42) in order to calculate the right-hand side

since  is a constant.
is a constant.
Corollary 2.8.
Under the hypothesis of Proposition 2.6,

Proof.
From (1.6) it follows that the formula in the statement is equivalent to

We prove this last relation. Substituting (2.32) and (2.33), it suffices to show that

Now, written  in terms of
in terms of  as in (2.20), the previous relation becomes
as in (2.20), the previous relation becomes

and it is true according to (2.42).
3. Some Solutions
We state a necessary and sufficient condition in terms of the data  .
.
Theorem 3.1.
Let  be a MOPS such that
be a MOPS such that  ,
,  and
and  . Also assume
. Also assume  , for all
, for all  . We define recursively a sequence
. We define recursively a sequence  of monic polynomials by the relations
of monic polynomials by the relations

and  with
with  ,
,  ,
,  . Then,
. Then,  is a MOPS different from
is a MOPS different from  if and only if the following formulas hold:
if and only if the following formulas hold:
-
(i)
 ,
, -
(ii)
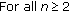 ,
, 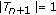 , where
, where  is defined by (2.16),
is defined by (2.16), -
(iii)
there exist two complex numbers
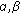 such that
such that (3.2)
(3.2) -
(iv)
 (3.3)
(3.3) -
(v)
 (3.4)
(3.4) -
(vi)
 (3.5)
(3.5)
Moreover, the sequences  and
and  are connected by
are connected by

Proof.
It only remains to establish the sufficient condition.
We first show that (3.6) implies (3.1)

The task is now to obtain that the expression in the brackets is null. Using (1.8), this expression becomes

Therefore, the result follows immediately from (3.5).
In order to obtain  , we take
, we take  in (3.6)
in (3.6)

Substituting (3.5) and (3.3), we get

Using (3.2) and (3.4), it is easy to check that

Now, we show that the sequence given by (3.6) satisfies (1.4) with  , then it is a MOPS.
, then it is a MOPS.
We will apply (1.12) as well as  , since
, since 

If we show that the coefficient of  is null and the coefficient of
is null and the coefficient of  is
is  , then (1.4) is true.
, then (1.4) is true.
At first, we compute the coefficient of  .
.

and this is equal to zero from (3.3).
We can obtain the coefficient of  by observation of (3.13). It is easy to see that this coefficient is
by observation of (3.13). It is easy to see that this coefficient is  . By virtue of (3.9) it is equal to
. By virtue of (3.9) it is equal to  , and then the required result follows.
, and then the required result follows.
Finally, the condition  follows from (3.11) by using the same method as in the proof of (2.35).
follows from (3.11) by using the same method as in the proof of (2.35).
Observe that condition (i) together with (3.6) gives  .
.
Corollary 3.2.
Under the same conditions as in the previous theorem, the following relations hold
-
(i)
 (3.14)
(3.14)
where  .
.
-
(ii)
 (3.15)
(3.15)
where  .
.
-
(iii)
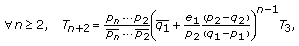 (3.16)
(3.16)
-
(iv)
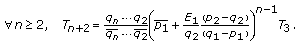 (3.17)
(3.17)
Proof.
We obtain  and
and  from (2.22) and (2.23) for
from (2.22) and (2.23) for  , respectively. The items (iii) and (iv) are straightforward from (2.20) and (2.21).
, respectively. The items (iii) and (iv) are straightforward from (2.20) and (2.21).
Now, we are going to express the Verblunsky coefficients for the solutions in terms of  and
and  . We remember that to give a MOPS
. We remember that to give a MOPS  on the unit circle is equivalent to know the sequence of complex numbers
on the unit circle is equivalent to know the sequence of complex numbers  with
with  .
.
Theorem 3.3.
Let  and
and  be two sequences of complex numbers such that
be two sequences of complex numbers such that
-
(i)
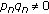 and
and 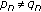 , for all
, for all 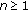 ,
, -
(ii)
 and
and 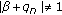 , for all
, for all 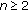 , where
, where 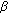 is given by (3.15) and
is given by (3.15) and 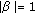 ,
, -
(iii)
 and
and  , for all
, for all 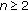 , where
, where  is given by (3.14),
is given by (3.14), -
(iv)
 , for all
, for all  .
.
Then, the only MOPS solutions of (3.1), such that  for all
for all  , verify
, verify

Moreover, the sequences  and
and  are connected by
are connected by

Proof.
In order to obtain  and
and  we use the hypothesis (iv) as well as (2.33)–(3.16) and (2.34)–(3.17), respectively. The conditions
we use the hypothesis (iv) as well as (2.33)–(3.16) and (2.34)–(3.17), respectively. The conditions  , follow from (ii) and (iii), respectively.
, follow from (ii) and (iii), respectively.
Applying  in (3.6), it holds that
in (3.6), it holds that

Combining with (2.13), we get

Again from (2.22) we get

This completes the proof because of the symmetry of the problem.
Remark 3.4.
Notice that the restrictions given for  and
and  in the previous theorem ensure that the sequences generated by
in the previous theorem ensure that the sequences generated by  and
and  are MPOS, but they do not ensure that
are MPOS, but they do not ensure that  and
and  fulfill (3.1). In fact, other similar conditions to (2.42) seem to be necessary in order to obtain a characterization of the Verblunsky coefficients in terms of
fulfill (3.1). In fact, other similar conditions to (2.42) seem to be necessary in order to obtain a characterization of the Verblunsky coefficients in terms of  and
and  .
.
4. Linear Functionals
In this section we establish the relation between the regular functionals associated with the sequences  and
and  .
.
Proposition 4.1.
Let  and
and  be the regular functionals normalized by
be the regular functionals normalized by  and
and  associated with
associated with  and
and  , respectively. Then, the following relation holds
, respectively. Then, the following relation holds

Proof.
We will show that

wherefrom the result follows because  is a basis in
is a basis in  .
.
If  the equality is trivial by definition of
the equality is trivial by definition of  .
.
If  , the left-hand side in (4.1) is
, the left-hand side in (4.1) is

where the last equality follows from (2.34).
We compute the right-hand side using(2.31)

In the same way, by virtue of (2.33), the right-hand side is equal to  Therefore, it only remains to check the equality
Therefore, it only remains to check the equality  . In order to do this we take the conjugate in (2.35), obtaining
. In order to do this we take the conjugate in (2.35), obtaining

Finally, we see that the equality  is true due to (3.14) and (3.15).
is true due to (3.14) and (3.15).
Remark 4.2.
The opposite question has been proved in [8]. That is, if  and
and  are regular functionals related by (4.1) with
are regular functionals related by (4.1) with  , then the corresponding orthogonal polynomials satisfy (2.1).
, then the corresponding orthogonal polynomials satisfy (2.1).
5. Carathéodory's Functions
In this section we obtain the relation between the Carathéodory functions associated with the sequences  and
and  . We denote by
. We denote by  the sequence of the moments corresponding to
the sequence of the moments corresponding to  , that is,
, that is,  , for all
, for all  .
.
Proposition 5.1.
Let  and
and  be the Carathéodory functions associated with
be the Carathéodory functions associated with  and
and  , respectively. Then,
, respectively. Then,  is the following rational transformation of
is the following rational transformation of  :
:

Proof.
Indeed, from (1.13)  , thus
, thus

Using (4.1), it holds that  . Therefore,
. Therefore,

wherefrom

Putting  and
and  we find (5.1).
we find (5.1).
References
Geronimus YL: Polynomials orthogonal on a circle and their applications. American Mathematical Society Translations, Series 1 1962, 3: 1-78.
Simon B: Orthogonal Polynomials on the Unit Circle, AMS Colloquium Publications. Volume 54. American Mathematical Society, Providence, RI, USA; 2005.
Szegö G: Orthogonal Polynomials, AMS Colloquium Publications. Volume 23. 4th edition. American Mathematical Society, Providence, RI, USA; 1975.
Alfaro M, Marcellán F, Peña A, Rezola ML: On linearly related orthogonal polynomials and their functionals. Journal of Mathematical Analysis and Applications 2003,287(1):307-319. 10.1016/S0022-247X(03)00565-1
Kwon KH, Lee JH, Marcellán F: Orthogonality of linear combinations of two orthogonal polynomial sequences. Journal of Computational and Applied Mathematics 2001,137(1):109-122. 10.1016/S0377-0427(00)00702-0
Maroni P: Prolégomènes à l'étude des polynômes orthogonaux semi-classiques. Annali di Matematica Pura ed Applicata 1987,149(4):165-184. 10.1007/BF01773932
Marcellán F, Peherstorfer F, Steinbauer R: Orthogonality properties of linear combinations of orthogonal polynomials. II. Advances in Computational Mathematics 1997,7(3):401-428. 10.1023/A:1018963323132
Suárez C: On second kind polynomials associated with rational transformations of linear functionals. Journal of Mathematical Analysis and Applications 2009,358(1):148-158. 10.1016/j.jmaa.2009.04.058
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Suárez, C. On Linear Combinations of Two Orthogonal Polynomial Sequences on the Unit Circle. Adv Differ Equ 2010, 406231 (2010). https://doi.org/10.1155/2010/406231
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/406231
 is Hermitian if
is Hermitian if  ,
,  ;
; is regular or quasidefinite (positive definite) if the principal minors of the moment matrix are nonsingular (positive), that is,
is regular or quasidefinite (positive definite) if the principal minors of the moment matrix are nonsingular (positive), that is,
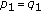 , then
, then  and
and 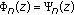 , for all
, for all  ,
,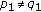 and
and 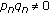 , for all
, for all  , then
, then  , for all
, for all 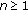 ,
, and
and  , for all
, for all 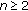 , then
, then  if and only if
if and only if 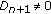 , for all
, for all  . Moreover,
. Moreover,  for all
for all  .
. using equalities (2.2)–(2.4) and (2.3)–(2.5). By doing this, we get
using equalities (2.2)–(2.4) and (2.3)–(2.5). By doing this, we get 
 such that
such that 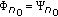 . From (2.1), written for
. From (2.1), written for 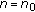 , it holds that
, it holds that  and then
and then  , and thus successively.
, and thus successively. , for all
, for all 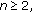
 and
and 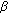 with
with 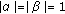 such that
such that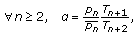
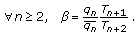
 and
and  are given by
are given by  and
and  ,
,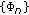 and
and 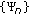 are connected by the following formulas:
are connected by the following formulas:

 ,
,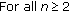 ,
, 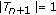 , where
, where  is defined by (2.16),
is defined by (2.16),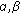 such that
such that





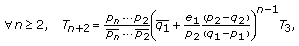
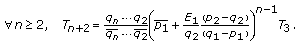
 and
and  , for all
, for all 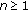 ,
, and
and 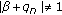 , for all
, for all 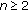 , where
, where 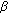 is given by (3.15) and
is given by (3.15) and 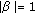 ,
, and
and  , for all
, for all 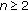 , where
, where  is given by (3.14),
is given by (3.14), , for all
, for all  .
.