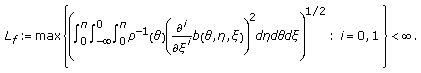- Research Article
- Open access
- Published:
Asymptotically Almost Periodic Solutions for Abstract Partial Neutral Integro-Differential Equation
Advances in Difference Equations volume 2010, Article number: 310951 (2010)
Abstract
The existence of asymptotically almost periodic mild solutions for a class of abstract partial neutral integro-differential equations with unbounded delay is studied.
1. Introduction
In this paper, we study the existence of asymptotically almost periodic mild solutions for a class of abstract partial neutral integro-differential equations modelled in the form

where  and
and  ,
,  , are closed linear operators;
, are closed linear operators;  is a Banach space; the history
is a Banach space; the history  ,
,  , belongs to some abstract phase space
, belongs to some abstract phase space  defined axiomatically
defined axiomatically  are appropriated functions.
are appropriated functions.
The study of abstract neutral equations is motivated by different practical applications in different technical fields. The literature related to ordinary neutral functional differential equations is very extensive and we refer the reader to Chukwu [1], Hale and Lunel [2], Wu [3], and the references therein. As a practical application, we note that the equation

arises in the study of the dynamics of income, employment, value of capital stock, and cumulative balance of payment; see [1] for details. In the above system,  is a real number, the state
is a real number, the state  ,
,  ,
,  are
are  continuous functions matrices,
continuous functions matrices,  is a constant
is a constant  matrix,
matrix,  represents the government intervention, and
represents the government intervention, and  the private initiative. We note that by assuming the solution
the private initiative. We note that by assuming the solution  is known on
is known on  , we can transform this system into an abstract system with unbounded delay described as (1.1).
, we can transform this system into an abstract system with unbounded delay described as (1.1).
Abstract partial neutral differential equations also appear in the theory of heat conduction. In the classic theory of heat conduction, it is assumed that the internal energy and the heat flux depend linearly on the temperature  and on its gradient
and on its gradient  . Under these conditions, the classic heat equation describes sufficiently well the evolution of the temperature in different types of materials. However, this description is not satisfactory in materials with fading memory. In the theory developed in [4, 5], the internal energy and the heat flux are described as functionals of
. Under these conditions, the classic heat equation describes sufficiently well the evolution of the temperature in different types of materials. However, this description is not satisfactory in materials with fading memory. In the theory developed in [4, 5], the internal energy and the heat flux are described as functionals of  and
and  . The next system, see for instance [6–9], has been frequently used to describe this phenomenon,
. The next system, see for instance [6–9], has been frequently used to describe this phenomenon,

In this system,  is open, bounded, and with smooth boundary;
is open, bounded, and with smooth boundary;  ;
;  represents the temperature in
represents the temperature in  at the time
at the time  ;
;  is a physical constant
is a physical constant  ,
,  are the internal energy and the heat flux relaxation, respectively. By assuming that the solution
are the internal energy and the heat flux relaxation, respectively. By assuming that the solution  is known on
is known on  and
and  , we can transform this system into an abstract system with unbounded delay described in the form (1.1).
, we can transform this system into an abstract system with unbounded delay described in the form (1.1).
Recent contributions on the existence of solutions with some of the previously enumerated properties or another type of almost periodicity to neutral functional differential equations have been made in [10, 11], for the case of neutral ordinary differential equations, and in [12–15] for partial functional differential systems.
The purpose of this work is to study the existence of asymptotically almost periodic mild solutions for the neutral system (1.1). To this end, we study the existence and qualitative properties of an exponentially stable resolvent operator for the integro-differential system

There exists an extensive literature related to the existence and qualitative properties of resolvent operator for integro-differential equations. We refer the reader to the book by Gripenberg et al. [16] which contains an overview of the theory for the case where the underlying space  has finite dimension. For abstract integro-differential equations described on infinite dimensional spaces, we cite the Prüss book [17] and the papers [18–20], Da Prato et al. [21, 22], and Lunardi [9, 23]. To finish this short description of the related literature, we cite the papers [24–26] where some of the above topics for the case of abstract neutral integro-differential equations with unbounded delay are treated.
has finite dimension. For abstract integro-differential equations described on infinite dimensional spaces, we cite the Prüss book [17] and the papers [18–20], Da Prato et al. [21, 22], and Lunardi [9, 23]. To finish this short description of the related literature, we cite the papers [24–26] where some of the above topics for the case of abstract neutral integro-differential equations with unbounded delay are treated.
To the best of our knowledge, the study of the existence of asymptotically almost periodic solutions of neutral integro-differential equations with unbounded delay described in the abstract form (1.1) is an untreated topic in the literature and this is the main motivation of this article.
To finish this section, we emphasize some notations used in this paper. Let  and
and  be Banach spaces. We denote by
be Banach spaces. We denote by  the space of bounded linear operators from
the space of bounded linear operators from  into
into  endowed with norm of operators, and we write simply
endowed with norm of operators, and we write simply  when
when  . By
. By  , we denote the range of a map
, we denote the range of a map  , and for a closed linear operator
, and for a closed linear operator  , the notation
, the notation  represents the domain of
represents the domain of  endowed with the graph norm,
endowed with the graph norm,  ,
,  . In the case
. In the case  , the notation
, the notation  stands for the resolvent set of
stands for the resolvent set of  and
and  is the resolvent operator of
is the resolvent operator of  . Furthermore, for appropriate functions
. Furthermore, for appropriate functions  and
and  , the notation
, the notation  denotes the Laplace transform of
denotes the Laplace transform of  and
and  the convolution between
the convolution between  and
and  , which is defined by
, which is defined by  . The notation
. The notation  stands for the closed ball with center at
stands for the closed ball with center at  and radius
and radius  in
in  . As usual,
. As usual,  represents the subspace of
represents the subspace of  formed by the functions which vanish at infinity.
formed by the functions which vanish at infinity.
2. Preliminaries
In this work, we will employ an axiomatic definition of the phase space  similar to that in [27]. More precisely,
similar to that in [27]. More precisely,  will denote a vector space of functions defined from
will denote a vector space of functions defined from  into
into  endowed with a seminorm denoted by
endowed with a seminorm denoted by  and such that the following axioms hold.
and such that the following axioms hold.
-
(A)
If
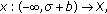 with
with 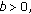 is continuous on
is continuous on 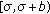 and
and  , then for each
, then for each 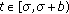 the following conditions hold:
the following conditions hold:-
(i)
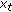 is in
is in  ,
, -
(ii)
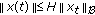 ,
, -
(iii)
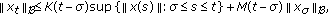 where
where 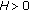 is a constant, and
is a constant, and 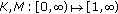 are functions such that
are functions such that 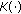 and
and 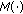 are respectively continuous and locally bounded, and
are respectively continuous and locally bounded, and 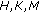 are independent of
are independent of 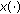 .
.
-
(i)
(A1) If  is a function as in
is a function as in  , then
, then  is a
is a  -valued continuous function on
-valued continuous function on  .
.
-
(B)
The space
 is complete.
is complete.
(C2) If  is a sequence in
is a sequence in  formed by functions with compact support such that
formed by functions with compact support such that uniformly on compact, then
uniformly on compact, then  and
and  as
as 
Remark 2.1.
In the remainder of this paper,  is such that
is such that

for every  continuous and bounded; see [27, Proposition
continuous and bounded; see [27, Proposition  ] for details.
] for details.
Definition 2.2.
Let  be the
be the  -semigroup defined by
-semigroup defined by  on
on  and
and  on
on  . The phase space
. The phase space  is called a fading memory if
is called a fading memory if  as
as  for each
for each  with
with  .
.
Remark 2.3.
In this work, we suppose that there exists a positive  such that
such that

for each  . Observe that this condition is verified, for example, if
. Observe that this condition is verified, for example, if  is a fading memory, see [27, Proposition
is a fading memory, see [27, Proposition  ].
].
Example 2.4 (The phase space  ).
).
 Let
Let  , and let
, and let be a nonnegative measurable function which satisfies the conditions (g-5) and (g-6) in the terminology of [27]. Briefly, this means that
be a nonnegative measurable function which satisfies the conditions (g-5) and (g-6) in the terminology of [27]. Briefly, this means that  is locally integrable, and there exists a nonnegative, locally bounded function
is locally integrable, and there exists a nonnegative, locally bounded function  on
on  such that
such that  for all
for all  and
and  , where
, where  is a set with Lebesgue measure zero. The space
is a set with Lebesgue measure zero. The space consists of all classes of functions
consists of all classes of functions such that
such that  is continuous on
is continuous on  , Lebesgue-measurable, and
, Lebesgue-measurable, and is Lebesgue integrable on
is Lebesgue integrable on  . The seminorm in
. The seminorm in is defined by
is defined by

The space satisfies axioms (A), (A-1), and (B). Moreover, when
satisfies axioms (A), (A-1), and (B). Moreover, when  and
and  , we can take
, we can take  ,
,  , and
, and  , for
, for  ; see [27, Theorem
; see [27, Theorem  ] for details.
] for details.
Now, we need to introduce some concepts, definitions, and technicalities on almost periodical functions.
Definition 2.5.
A function  is almost periodic (a.p.) if for every
is almost periodic (a.p.) if for every  , there exists a relatively dense subset of
, there exists a relatively dense subset of  , denoted by
, denoted by  , such that
, such that

Definition 2.6.
A function  is asymptotically almost periodic (a.a.p.) if there exists an almost periodic function
is asymptotically almost periodic (a.a.p.) if there exists an almost periodic function  and
and  such that
such that  .
.
The next lemmas are useful characterizations of a.p and a.a.p functions.
Lemma 2.7 (see [28, Theorem  ]).
]).
A function  is asymptotically almost periodic if and only if for every
is asymptotically almost periodic if and only if for every  there exist
there exist  and a relatively dense subset of
and a relatively dense subset of , denoted by
, denoted by  , such that
, such that

In this paper,  and
and  are the spaces
are the spaces

endowed with the norms  and
and  respectively. We know from the result in [28] that
respectively. We know from the result in [28] that  and
and  are Banach spaces.
are Banach spaces.
Next,  and
and  are abstract Banach spaces.
are abstract Banach spaces.
Definition 2.8.
Let  be an open subset of
be an open subset of 
-
(a)
A continuous function
 (resp.,
(resp., 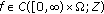 ) is called pointwise almost periodic (p.a.p.), (resp., pointwise asymptotically almost periodic (p.a.a.p.) if
) is called pointwise almost periodic (p.a.p.), (resp., pointwise asymptotically almost periodic (p.a.a.p.) if 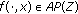 (resp.,
(resp.,  ) for every
) for every 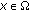 .
. -
(b)
A continuous function
 is called uniformly almost periodic (u.a.p.), if for every
is called uniformly almost periodic (u.a.p.), if for every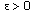 and every compact
and every compact 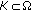 there exists a relatively dense subset of
there exists a relatively dense subset of 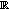 , denoted by
, denoted by 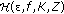 , such that
, such that 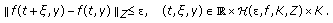 (2.7)
(2.7)
-
(c)
A continuous function
 is called uniformly asymptotically almost periodic (u.a.a.p.), if for every
is called uniformly asymptotically almost periodic (u.a.a.p.), if for every  and every compact
and every compact  there exists a relatively dense subset of
there exists a relatively dense subset of  , denoted by
, denoted by 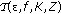 , and
, and 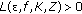 such that
such that 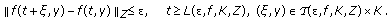 (2.8)
(2.8)
The next lemma summarizes some properties which are fundamental to obtain our results.
Lemma 2.9 (see [29, Theorem  ]).
]).
Let  be an open set. Then the following properties hold.
be an open set. Then the following properties hold.
-
(a)
If
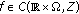 is p.a.p. and satisfies a local Lipschitz condition at
is p.a.p. and satisfies a local Lipschitz condition at 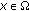 , uniformly at
, uniformly at  , then
, then 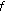 is u.a.p.
is u.a.p. -
(b)
If
 is p.a.a.p. and satisfies a local Lipschitz condition at
is p.a.a.p. and satisfies a local Lipschitz condition at 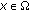 , uniformly at
, uniformly at  , then
, then  is u.a.a.p.
is u.a.a.p. -
(c)
If
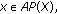 then
then . Moreover, if
. Moreover, if  is a fading memory space and
is a fading memory space and 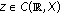 is such that
is such that  and
and  , then
, then .
. -
(d)
If
 is u.a.p. and
is u.a.p. and 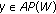 is such that
is such that  , then
, then .
. -
(e)
If
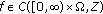 is u.a.a.p and
is u.a.a.p and  is such that
is such that  , then
, then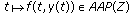 .
.
3. Resolvent Operators
In this section, we study the existence and qualitative properties of an exponentially resolvent operator for the integro-differential abstract Cauchy problem

The results obtained for the resolvent operator in this section are similar to those that can be found, for instance, in the papers [21, 23, 30]. In this paper, we prove the necessary estimates for the proof of an existence theorem of asymptotically almost periodic solutions for (1.1). For the better comprehension of the subject, we will introduce the following definitions, hypothesis, and results.
We introduce the following concept of resolvent operator for integro-differential problem (3.1).
Definition 3.1.
A one-parameter family of bounded linear operators  on
on  is called a resolvent operator of (3.1) if the following conditions are verified.
is called a resolvent operator of (3.1) if the following conditions are verified.
-
(a)
Function
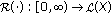 is strongly continuous and
is strongly continuous and 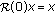 for all
for all 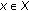 .
. -
(b)
For
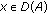 ,
,  , and
, and 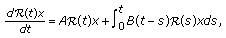 (3.2)
(3.2)

for every  ,
,
-
(c)
There exist constants
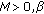 such that
such that 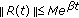 for every
for every 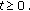
Definition 3.2.
A resolvent operator  of (3.1) is called exponentially stable if there exist positive constants
of (3.1) is called exponentially stable if there exist positive constants  such that
such that 
In this work, we always assume that the following conditions are verified.
(H1) The operator  is the infinitesimal generator of an analytic semigroup
is the infinitesimal generator of an analytic semigroup  on
on  , and there are constants
, and there are constants  , and
, and  such that
such that  and
and  for all
for all  .
.
(H2) For all 
 is a closed linear operator,
is a closed linear operator,  , and
, and  is strongly measurable on
is strongly measurable on  for each
for each  . There exists
. There exists  such that
such that  exists for
exists for  and
and  for all
for all  and
and  . Moreover, the operator valued function
. Moreover, the operator valued function  has an analytical extension (still denoted by
has an analytical extension (still denoted by  ) to
) to  such that
such that  for all
for all  , and
, and  as
as  .
.
(H3) There exist a subspace  dense in
dense in  and positive constants
and positive constants  ,
,  such that
such that  ,
,  , and
, and  for every
for every  and all
and all  .
.
In the sequel, for ,
,  , and
, and  , set
, set

and for ,
,  , the paths
, the paths

with  are oriented counterclockwise. In addition,
are oriented counterclockwise. In addition,  is the set
is the set

We next study some preliminary properties needed to establish the existence of a resolvent operator for the problem (3.1).
Lemma 3.3.
There exists  such that
such that  and the function
and the function  is analytic. Moreover,
is analytic. Moreover,

and there exist constants  for
for  such that
such that



for every  .
.
Proof.
Since

fixed  there exists a positive number
there exists a positive number  such that
such that  for
for  . Consequently, the operator
. Consequently, the operator  has a continuous inverse with
has a continuous inverse with  . Moreover, for
. Moreover, for  , we have
, we have

and for  ,
,

which shows (3.7) and that  . Now, from (3.7) we obtain
. Now, from (3.7) we obtain  and
and

Consequently,

the functions  are analytic, and estimates (3.8), and (3.10) are valid. In addition, for
are analytic, and estimates (3.8), and (3.10) are valid. In addition, for  , we can write
, we can write

for  sufficiently large. This proves (3.9) and completes the proof.
sufficiently large. This proves (3.9) and completes the proof.
Observation 1.
If  is a resolvent operator for (3.1), it follows from (3.3) that
is a resolvent operator for (3.1), it follows from (3.3) that  for all
for all  . Applying Lemma 3.3 and the properties of the Laplace transform, we conclude that
. Applying Lemma 3.3 and the properties of the Laplace transform, we conclude that  is the unique resolvent operator for (3.1).
is the unique resolvent operator for (3.1).
In the remainder of this section,  and
and  are numbers such that
are numbers such that  and
and  . Moreover, we denote by
. Moreover, we denote by  a generic constant that represents any of the constants involved in the statements of Lemma 3.3 as well as any other constant that arises in the estimate that follows. We now define the operator family
a generic constant that represents any of the constants involved in the statements of Lemma 3.3 as well as any other constant that arises in the estimate that follows. We now define the operator family  by
by

We will next establish that  is a resolvent operator for (3.1).
is a resolvent operator for (3.1).
Lemma 3.4.
The function  is exponentially bounded in
is exponentially bounded in  .
.
Proof.
If  , from (3.17) and estimate (3.8), we get
, from (3.17) and estimate (3.8), we get

On the other hand, using that  is analytic on
is analytic on  , for
, for  , we obtain
, we obtain

This complete the proof.
Lemma 3.5.
The operator function  is exponentially bounded in
is exponentially bounded in  .
.
Proof.
It follows from (3.9) that the integral in

is absolutely convergent in  and defines a linear operator
and defines a linear operator  . Using that
. Using that  is closed, we can affirm that
is closed, we can affirm that  . From Lemma 3.3,
. From Lemma 3.3,  is analytic and
is analytic and  . If
. If  and
and  , we have
, we have

For  and
and  , we get
, we get

From before and Lemma 3.4, we infer that  is exponentially bounded in
is exponentially bounded in  . The proof is finished.
. The proof is finished.
Lemma 3.6.
The function  is strongly continuous.
is strongly continuous.
Proof.
It is clear from (3.17) that  is continuous at
is continuous at  for every
for every  . We next establish the continuity at
. We next establish the continuity at  . Let
. Let  and
and  be sufficiently large, using that
be sufficiently large, using that

where  represent the curve
represent the curve  for
for  .
.
For  and
and  , we get
, we get

Furthermore, it follows from (3.8), and assumption (H2) that

where  is integrable for
is integrable for  . From the Lebesgue dominated convergence theorem, we infer that
. From the Lebesgue dominated convergence theorem, we infer that

Let now  be the curve
be the curve  for
for  . Turning to apply Cauchy's theorem combining with the estimate
. Turning to apply Cauchy's theorem combining with the estimate

we obtain

we can affirm that  for all
for all  , which completes and the proof since
, which completes and the proof since  is dense in
is dense in  and
and  is bounded on
is bounded on  .
.
Notice that  the sectors
the sectors  from Lemma 3.3,
from Lemma 3.3,  is analytic. Consider the contours
is analytic. Consider the contours

and  oriented counterclockwise. By Cauchy theorem for
oriented counterclockwise. By Cauchy theorem for  , we obtain
, we obtain

The following estimate:

is the one responsible for the fact that the integral  tends to
tends to  as
as  tend to
tend to  in a similar way the integral
in a similar way the integral  tend to
tend to  as
as  tend to
tend to  so that
so that

For  , we obtain
, we obtain

and proceeding as before, we obtain  for all
for all  which ends the proof.
which ends the proof.
The following result can be proved with an argument similar to that used in the proof of the preceding lemma with changing by
by 
Lemma 3.7.
The function  is strongly continuous.
is strongly continuous.
We next set  .
.
Lemma 3.8.
The function  has an analytic extension to
has an analytic extension to  , and
, and

Proof.
For  and
and  , we can write
, we can write  where
where  ,
,  and
and  If
If  , from (3.8) and (3.17), we obtain
, from (3.8) and (3.17), we obtain

Using that  is analytic on
is analytic on  , for
, for  ,
,  , we get
, we get

This property allows us to define the extension  by this integral.
by this integral.
Similarly, the integral on the right hand side of (3.34) is also absolutely convergent in  and strong, continuous on
and strong, continuous on  for
for  . For
. For  ,
,

where  is integrable for
is integrable for  . From the Lebesgue dominated convergence theorem, we obtain that
. From the Lebesgue dominated convergence theorem, we obtain that  verifies (3.34). The proof is ended.
verifies (3.34). The proof is ended.
Lemma 3.9.
For every  with
with  ,
,  .
.
Proof.
Using that  is analytic on
is analytic on  and that the integrals involved in the calculus are absolutely convergent, we have
and that the integrals involved in the calculus are absolutely convergent, we have

Theorem 3.10.
The function  is a resolvent operator for the system (3.1).
is a resolvent operator for the system (3.1).
Proof.
Let  . From Lemma 3.9, for
. From Lemma 3.9, for  ,
,

which implies

Applying [31, Proposition  , Corollary
, Corollary  ], we get
], we get

which in turn implies that

Arguing as above but using the equality  we obtain that (3.2) holds.
we obtain that (3.2) holds.
On the other hand, by Lemma 3.8 we infer that  . Next, we analyze the differentiability on
. Next, we analyze the differentiability on  . Let
. Let  and
and  for all
for all  we can choose
we can choose  such that
such that

For  and
and  , there exists
, there exists  such that
such that

Consequently, for  we have that
we have that

which proves the existence of the right derivative of  at zero and that
at zero and that  This proves that resolvent equation (3.3) is valid for every
This proves that resolvent equation (3.3) is valid for every  and
and  for every
for every  . This completes the proof.
. This completes the proof.
Corollary 3.11.
If  then the function
then the function  is an exponentially stable resolvent operator for the system (3.1).
is an exponentially stable resolvent operator for the system (3.1).
In the next result, we denote by  the fractional power of the operator
the fractional power of the operator  (see [32] for details).
(see [32] for details).
Theorem 3.12.
Suppose that the conditions  are satisfied. Then there exists a positive number
are satisfied. Then there exists a positive number  such that
such that

for all 
Proof.
Let  From [32, Theorem
From [32, Theorem  ], there exists
], there exists  such that
such that

Since  is a
is a  valued function, for all
valued function, for all 

where  is independent of
is independent of  . From (3.48), we get for
. From (3.48), we get for 

On the other hand, using that  is analytic on
is analytic on  , for
, for  , we get
, we get

From the previous facts, we conclude that

which ends the proof.
Corollary 3.13.
If  and
and  , then there exists
, then there exists  such that
such that

In the remainder of this section, we discuss the existence and regularity of solutions of


where  . In the sequel,
. In the sequel,  is the operator function defined by (3.17). We begin by introducing the following concept of classical solution.
is the operator function defined by (3.17). We begin by introducing the following concept of classical solution.
Definition 3.14.
A function  ,
,  , is called a classical solution of (3.53)-(3.54) on
, is called a classical solution of (3.53)-(3.54) on  if
if  , the condition (3.54) holds and (3.53) is verified on
, the condition (3.54) holds and (3.53) is verified on  .
.
The next result has been established in [30].
Theorem 3.15 ([30, Theorem  ]).
]).
Let  . Assume that
. Assume that  and
and  is a classical solution of (3.53)-(3.54) on
is a classical solution of (3.53)-(3.54) on  . Then
. Then

An immediate consequence of the above theorem is the uniqueness of classical solutions.
Corollary 3.16.
If  are classical solutions of (3.53)-(3.54) on
are classical solutions of (3.53)-(3.54) on  , then
, then  on
on  .
.
Motivated by (3.55), we introduce the following concept.
Definition 3.17.
A function  is called a mild solution of (3.53)-(3.54) if
is called a mild solution of (3.53)-(3.54) if

4. Existence Result of Asymptotically Almost Periodic Solutions
In this section, we study the existence of asymptotically almost periodic mild solutions for the abstract integro-differential system (1.1). To establish our existence result, motivated by the previous section we introduce the following assumptions.
(P1) There exists a Banach space  continuously included in
continuously included in  such that the following conditions are verified.
such that the following conditions are verified.
-
(a)
For every
 ,
, 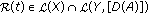 and
and 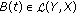 . In addition,
. In addition, 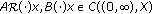 for every
for every  .
. -
(b)
There are positive constants
 such that
such that  (4.1)
(4.1)
-
(c)
There exists
 such that
such that
(P2) The continuous function  is p.a.a.p, and there exists a continuous function
is p.a.a.p, and there exists a continuous function  such that
such that

(P3) The continuous function  is p.a.a.p, and there exists a continuous function
is p.a.a.p, and there exists a continuous function  such that
such that

Motivated by the theory of resolvent operator, we introduce the following concept of mild solution for (1.1).
Definition 4.1.
A function  is called a mild solution of (1.1) on
is called a mild solution of (1.1) on  , if
, if 
 the functions
the functions and
and are integrable on
are integrable on  for every
for every  and
and

Lemma 4.2.
Let condition  hold and let
hold and let  be a function in
be a function in  . If
. If  is the function defined by
is the function defined by  then
then  .
.
Proof.
Let  . Let
. Let  ,
,  be as in Lemma 2.7 and
be as in Lemma 2.7 and  such that
such that  . For
. For  and
and  , we get
, we get

which implies that

Now, from inequality (4.6) and Lemma 2.7, we conclude that  is a.a.p. The proof is complete.
is a.a.p. The proof is complete.
Lemma 4.3.
Assume that the condition  is fulfilled. Let
is fulfilled. Let  and let
and let  be the function defined by
be the function defined by

Then  .
.
Proof.
Let  ,
,  be as in Lemma 2.7 and
be as in Lemma 2.7 and  such that
such that

for  where
where  . For
. For  and
and  , we get
, we get

We obtain

which implies that

From inequality (4.11) and Lemma 2.7, we conclude that  is a.a.p., which ends the proof.
is a.a.p., which ends the proof.
Now, we can establish our existence result.
Theorem 4.4.
Assume that  is a fading memory space and
is a fading memory space and 
 , and
, and  are held. If
are held. If  and
and  for every
for every  , then there exists
, then there exists  such that for each
such that for each  , there exists a mild solution,
, there exists a mild solution,  , of (1.1) on
, of (1.1) on  such that
such that  and
and  .
.
Proof.
Let  and
and  be such that
be such that

where  is the constant introduced in Remark 2.3. We affirm that the assertion holds for
is the constant introduced in Remark 2.3. We affirm that the assertion holds for  Let
Let  On the space
On the space

endowed with the metric  , we define the operator
, we define the operator  by
by

where  is the function defined by the relation
is the function defined by the relation  and
and  on
on  . From the hypothesis
. From the hypothesis 
 , and
, and  , we obtain that
, we obtain that  is well defined and that
is well defined and that  Moreover, from Lemmas 4.2 and 4.3 it follows that
Moreover, from Lemmas 4.2 and 4.3 it follows that  .
.
Next, we prove that  is a contraction from
is a contraction from  into
into  . If
. If  and
and  , we get
, we get

where the inequality  has been used and
has been used and  represent the continuous inclusion of
represent the continuous inclusion of  on
on  . Thus,
. Thus,  . On the other hand, for
. On the other hand, for  we see that
we see that

which shows that  is a contraction from
is a contraction from  into
into  The assertion is now a consequence of the contraction mapping principle. The proof is complete.
The assertion is now a consequence of the contraction mapping principle. The proof is complete.
5. Applications
In this section, we study the existence of asymptotically almost periodic solutions of the partial neutral integro-differential system

for  ,
,  , and
, and  Moreover, we have identified
Moreover, we have identified  .
.
To represent this system in the abstract form (1.1), we choose the spaces  and
and  ; see Example 2.4 for details. We also consider the operators
; see Example 2.4 for details. We also consider the operators  ,
,  , given by
, given by  ,
,  for
for  Moreover,
Moreover,  has discrete spectrum, the eigenvalues are
has discrete spectrum, the eigenvalues are  ,
,  with corresponding eigenvectors
with corresponding eigenvectors  , and the set of functions
, and the set of functions  is an orthonormal basis of
is an orthonormal basis of  and
and  for
for  . For
. For  from [32] we can define the fractional power
from [32] we can define the fractional power  of
of  is given by
is given by  where
where  In the next theorem, we consider
In the next theorem, we consider  . We observe that
. We observe that  and
and  for
for  from [33, Proposition
from [33, Proposition  ], we obtain that
], we obtain that  is a sectorial operator satisfying
is a sectorial operator satisfying  Moreover, it is easy to see that conditions (H2)-(H3) in Section 3 are satisfied with
Moreover, it is easy to see that conditions (H2)-(H3) in Section 3 are satisfied with  , and
, and  is the space of infinitely differentiable functions that vanish at
is the space of infinitely differentiable functions that vanish at  and
and  . Under the above conditions, we can represent the system
. Under the above conditions, we can represent the system

in the abstract form

We define the functions  by
by

where
-
(i)
the functions
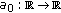 are continuous and
are continuous and  ;
; -
(ii)
the functions
 ,
, 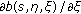 are measurable,
are measurable, 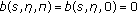 for all
for all  and
and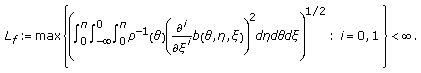 (5.5)
(5.5)
Moreover,  are bounded linear operators,
are bounded linear operators,  ,
,  , and a straightforward estimation using (ii) shows that
, and a straightforward estimation using (ii) shows that  and
and

for all  . This allows us to rewrite the system (5.1) in the abstract form (1.1) with
. This allows us to rewrite the system (5.1) in the abstract form (1.1) with 
Theorem 5.1.
Assume that the previous conditions are verified. Let  and
and  such that
such that  then there exists a mild solution
then there exists a mild solution  of (5.1) with
of (5.1) with  .
.
Proof.
For  from
from  , we obtain
, we obtain

since  . By using a similar procedure as in the proofs of Lemma 3.3 and Theorem 3.10, we obtain the existence of resolvent operator for (5.2). From the hypothesis, we obtain
. By using a similar procedure as in the proofs of Lemma 3.3 and Theorem 3.10, we obtain the existence of resolvent operator for (5.2). From the hypothesis, we obtain  by the Lemma 3.3, Corollaries 3.11 and 3.13, the assumption
by the Lemma 3.3, Corollaries 3.11 and 3.13, the assumption  is satisfied. From Theorem 4.4, the proof is complete.
is satisfied. From Theorem 4.4, the proof is complete.
References
Chukwu EN: Differential Models and Neutral Systems for Controlling the Wealth of Nations, Advances in Mathematics for Applied Sciences. Volume 54. World Scientific Publishing, River Edge, NJ, USA; 2001:xvi+513.
Hale J, Lunel SM: Introduction to Functional-Differential Equations. Applied Mathematical Sciences. Volume 99. Springer, New York, NY, USA; 1993.
Wu J: Theory and Applications of Partial functional-Differential Equations, Applied Mathematical Sciences. Volume 119. Springer, New York, NY, USA; 1996:x+429.
Gurtin ME, Pipkin AC: A general theory of heat conduction with finite wave speeds. Archive for Rational Mechanics and Analysis 1968,31(2):113-126. 10.1007/BF00281373
Nunziato J: On heat conduction in materials with memory. Quarterly of Applied Mathematics 1971, 29: 187-204.
Cannarsa P, Sforza D: Global solutions of abstract semilinear parabolic equations with memory terms. Nonlinear Differential Equations and Applications 2003,10(4):399-430. 10.1007/s00030-003-1004-2
Clément Ph, Nohel J: Asymptotic behavior of solutions of nonlinear Volterra equations with completely positive kernels. SIAM Journal on Mathematical Analysis 1981,12(4):514-535. 10.1137/0512045
Clément P, Philippe J: Global existence for a semilinear parabolic Volterra equation. Mathematische Zeitschrift 1992,209(1):17-26. 10.1007/BF02570816
Lunardi A: On the linear heat equation with fading memory. SIAM Journal on Mathematical Analysis 1990,21(5):1213-1224. 10.1137/0521066
Man NM, Minh NV: On the existence of quasi periodic and almost periodic solutions of neutral functional differential equations. Communications on Pure and Applied Analysis 2004,3(2):291-300. 10.3934/cpaa.2004.3.291
Yuan R: Existence of almost periodic solutions of neutral functional-differential equations via Liapunov-Razumikhin function. Zeitschrift für Angewandte Mathematik und Physik 1998,49(1):113-136. 10.1007/s000330050084
Diagana T, Henríquez HR, Hernández EM: Almost automorphic mild solutions to some partial neutral functional-differential equations and applications. Nonlinear Analysis: Theory, Methods & Applications 2008,69(5-6):1485-1493. 10.1016/j.na.2007.06.048
Hernández E, Henríquez H: Existence of periodic solutions of partial neutral functional-differential equations with unbounded delay. Journal of Mathematical Analysis and Applications 1998,221(2):499-522. 10.1006/jmaa.1997.5899
Hernández E, Pelicer M: Asymptotically almost periodic and almost periodic solutions for partial neutral differential equations. Applied Mathematics Letters 2005,18(11):1265-1272. 10.1016/j.aml.2005.02.015
Hernández E, Diagana T: Existence and uniqueness of pseudo almost periodic solutions to some abstract partial neutral functional-differential equations and applications. Journal of Mathematical Analysis and Applications 2007,327(2):776-791. 10.1016/j.jmaa.2006.04.043
Gripenberg G, Londen S-O, Staffans O: Volterra Integral and Functional Equations, Encyclopedia of Mathematics and Its Applications. Volume 34. Cambridge University Press, Cambridge, UK; 1990:xxii+701.
Prüss J: Evolutionary Integral Equations and Applications, Monographs in Mathematics. Volume 87. Birkhäuser, Basel, Switzerland; 1993:xxvi+366.
Grimmer R: Resolvent operators for integral equations in a Banach space. Transactions of the American Mathematical Society 1982,273(1):333-349. 10.1090/S0002-9947-1982-0664046-4
Grimmer RC, Kappel F: Series expansions for resolvents of Volterra integro-differential equations in Banach space. SIAM Journal on Mathematical Analysis 1984,15(3):595-604. 10.1137/0515045
Grimmer RC, Pritchard AJ: Analytic resolvent operators for integral equations in Banach space. Journal of Differential Equations 1983,50(2):234-259. 10.1016/0022-0396(83)90076-1
Da Prato G, Iannelli M: Existence and regularity for a class of integro-differential equations of parabolic type. Journal of Mathematical Analysis and Applications 1985,112(1):36-55. 10.1016/0022-247X(85)90275-6
Da Prato G, Lunardi A: Solvability on the real line of a class of linear Volterra integro-differential equations of parabolic type. Annali di Matematica Pura ed Applicata 1988,150(1):67-117. 10.1007/BF01761464
Lunardi A: Laplace transform methods in integro-differential equations. Journal of Integral Equations 1985,10(1–3):185-211.
Henriquez H, Hernández E, dos Santos JPC: Asymptotically almost periodic and almost periodic solutions for partial neutral integrodifferential equations. Zeitschrift für Analysis und ihre Anwendungen 2007,26(3):363-375. 10.4171/ZAA/1329
Hernández E, dos Santos JPC: Existence results for partial neutral integro-differential equation with unbounded delay. Applicable Analysis 2007,86(2):223-237. 10.1080/00036810601148216
Henriquez HR, Hernández E, dos Santos JPC: Existence results for abstract partial neutral integro-differential equation with unbounded delay. Electronic Journal of Qualitative Theory of Differential Equations 2009, 29: 1-23.
Hino Y, Murakami S, Naito T: Functional-Differential Equations with Infinite Delay, Lecture Notes in Mathematics. Volume 1473. Springer, Berlin, Germany; 1991:x+317.
Zaidman S: Almost-Periodic Functions in Abstract Spaces, Research Notes in Mathematics. Volume 126. Pitman (Advanced Publishing Program), Boston, Mass, USA; 1985:iii+133.
Yoshizawa T: Stability Theory and the Existence of Periodic Solutions and Almost Periodic Solutions. Volume 14. Springer, New York, NY, USA; 1975:vii+233.
Grimmer R, Prüss J: On linear Volterra equations in Banach spaces. Computers & Mathematics with Applications 1985,11(1–3):189-205. 10.1016/0898-1221(85)90146-4
Arendt W, Batty C, Hieber M, Neubrander F: Vector-Valued Laplace Transforms and Cauchy Problems, Monographs in Mathematics. Volume 96. Birkhäuser, Basel, Switzerland; 2001:xii+523.
Pazy A: Semigroups of linear operators and applications to partial differential equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Lunardi A: Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progress in Nonlinear Differential Equations and Their Applications. Volume 16. Birkhäuser, Basel, Switzerland; 1995:xviii+424.
Acknowledgment
José Paulo C. dos Santos is partially supported by FAPEMIG/Brazil under Grant CEX-APQ-00476-09.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
dos Santos, J.P.C., Guzzo, S.M. & Rabelo, M.N. Asymptotically Almost Periodic Solutions for Abstract Partial Neutral Integro-Differential Equation. Adv Differ Equ 2010, 310951 (2010). https://doi.org/10.1155/2010/310951
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/310951
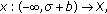 with
with 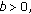 is continuous on
is continuous on 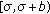 and
and  , then for each
, then for each 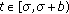 the following conditions hold:
the following conditions hold: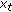 is in
is in  ,
,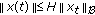 ,
,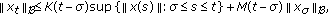 where
where 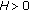 is a constant, and
is a constant, and 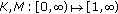 are functions such that
are functions such that 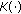 and
and 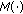 are respectively continuous and locally bounded, and
are respectively continuous and locally bounded, and 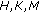 are independent of
are independent of 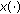 .
. is complete.
is complete. (resp.,
(resp., 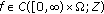 ) is called pointwise almost periodic (p.a.p.), (resp., pointwise asymptotically almost periodic (p.a.a.p.) if
) is called pointwise almost periodic (p.a.p.), (resp., pointwise asymptotically almost periodic (p.a.a.p.) if 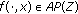 (resp.,
(resp.,  ) for every
) for every 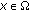 .
. is called uniformly almost periodic (u.a.p.), if for every
is called uniformly almost periodic (u.a.p.), if for every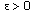 and every compact
and every compact 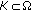 there exists a relatively dense subset of
there exists a relatively dense subset of 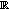 , denoted by
, denoted by 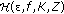 , such that
, such that 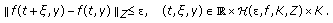
 is called uniformly asymptotically almost periodic (u.a.a.p.), if for every
is called uniformly asymptotically almost periodic (u.a.a.p.), if for every  and every compact
and every compact  there exists a relatively dense subset of
there exists a relatively dense subset of  , denoted by
, denoted by 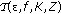 , and
, and 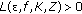 such that
such that 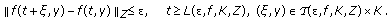
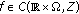 is p.a.p. and satisfies a local Lipschitz condition at
is p.a.p. and satisfies a local Lipschitz condition at  , uniformly at
, uniformly at  , then
, then 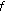 is u.a.p.
is u.a.p. is p.a.a.p. and satisfies a local Lipschitz condition at
is p.a.a.p. and satisfies a local Lipschitz condition at 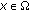 , uniformly at
, uniformly at  , then
, then  is u.a.a.p.
is u.a.a.p.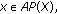 then
then . Moreover, if
. Moreover, if  is a fading memory space and
is a fading memory space and 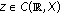 is such that
is such that  and
and  , then
, then .
. is u.a.p. and
is u.a.p. and 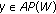 is such that
is such that  , then
, then .
.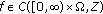 is u.a.a.p and
is u.a.a.p and  is such that
is such that  , then
, then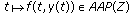 .
.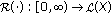 is strongly continuous and
is strongly continuous and 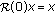 for all
for all 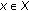 .
.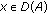 ,
,  , and
, and 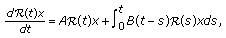
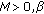 such that
such that 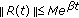 for every
for every 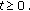
 ,
, 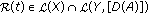 and
and 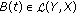 . In addition,
. In addition, 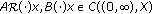 for every
for every  .
. such that
such that 
 such that
such that
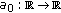 are continuous and
are continuous and  ;
; ,
, 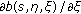 are measurable,
are measurable, 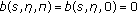 for all
for all  and
and