- Research Article
- Open access
- Published:
The Discrete Beverton-Holt Model with Periodic Harvesting in a Periodically Fluctuating Environment
Advances in Difference Equations volume 2010, Article number: 215875 (2010)
Abstract
We investigate the effect of constant and periodic harvesting on the Beverton-Holt model in a periodically fluctuating environment. We show that in a periodically fluctuating environment, periodic harvesting gives a better maximum sustainable yield compared to constant harvesting. However, if one can also fix the environment, then constant harvesting in a constant environment can be a better option, especially for sufficiently large initial populations. Also, we investigate the combinatorial structure of the periodic sequence of carrying capacities and its effect on the maximum sustainable yield. Finally, we leave some questions worth further investigations.
1. Introduction
In October 2008, the World Bank and the Food and Agriculture Organization of the United Nations released a study on the economic justification for fisheries reform [1]. The title of the report says it all "The Sunken Billions." The report argues that the sunken  Billions is a conservative estimate for the losses incurred annually due to carrying business as usual. In general, the study shows a grim picture on the current state of marine fish stocks. The recovery of the sunken billions and wasted harvesting efforts is obviously not an instantaneous process, but rather the product of two main strategies: reducing harvesting efforts and rebuilding of fish stocks. Clearly, the two are very well related; however, a good understanding of theoretical harvesting strategies on population models will go along way in designing an optimal strategy.
Billions is a conservative estimate for the losses incurred annually due to carrying business as usual. In general, the study shows a grim picture on the current state of marine fish stocks. The recovery of the sunken billions and wasted harvesting efforts is obviously not an instantaneous process, but rather the product of two main strategies: reducing harvesting efforts and rebuilding of fish stocks. Clearly, the two are very well related; however, a good understanding of theoretical harvesting strategies on population models will go along way in designing an optimal strategy.
There is a wealth of research on the effect of harvesting on the dynamics of populations governed by differential equations. For example, in predator-prey systems, constant harvesting can lead to the destabilization of population's equilibria, the creation of limit cycles, different types of bifurcations, catastrophe, and even chaotic behavior [2–7]. Optimal harvesting for single species has been studied by several authors from different points of view; see for example [8–10] and the references therein. Recently, Braverman and Mamadani [11] considered both autonomous and nonautonomous population models and found that constant harvesting is always superior to impulsive harvesting even though impulsive harvesting can sometimes do as good as constant harvesting. Their results contrast with the results of Ludwig [12] and Xu et al. [13]. For single species, Ludwig [12] studied models with random fluctuations and found that constant effort harvesting does worse than other harvesting strategies. Xu et al. [13] investigated harvesting in seasonal environments of a population with logistic growth and found that pulse harvesting is usually the dominant strategy and that the yield depends dramatically on the intrinsic growth rate of population and the magnitude of seasonality. Furthermore, for large intrinsic growth rate and small environmental variability, several strategies such as constant exploitation rate, pulse harvest, linear exploitation rate, and time-dependent harvest are quite effective and have comparable maximum sustainable yields. However, for populations with small intrinsic growth rate but subject to large seasonality, none of these strategies is particularly effective, but still pulse harvesting provides the best maximum sustainable yield.
Although the subject of difference equations and discrete models has been flourishing in the past two decades, harvesting in discrete population models is relatively morbid. Constant rate depletion on the discrete Ricker model was studied in [14], where it was shown numerically that populations exhibiting chaotic oscillations are not necessarily vulnerable to extinction. The effect of periodic harvesting on the discrete Ricker model and for a host-parasite model was studied in [15]. The stochastic Beverton-Holt equation with constant and proportional harvesting was studied in [16]. A special type of periodic impulsive harvesting in relation with seasonal environment was also studied in [17]. In [18], AlSharawi and Rhouma examined the effect of harvesting and stocking on competing species governed by a Leslie/Gower model and found that careful harvesting of the dominant species in an exclusive competitive environment can sometimes lead to the survival of the weaker species. More recently, the authors have also studied the Beverton-Holt equation under periodic and conditional harvesting and have found that in a constant capacity environment, constant rate harvesting is the optimal strategy [19].
This paper is a continuation of [19] and it is a modest contribution toward a full understanding of harvesting strategies on discrete population models. We compare the effect of different harvesting strategies in different environments. In particular, we consider and compare the effect of periodic and constant harvesting in both constant and periodic environments in a population governed by the Beverton-Holt model

where  is the population inherent growth rate and
is the population inherent growth rate and  is the population carrying capacity at time
is the population carrying capacity at time  In our analysis, we focus on the maximum sustainable yield commonly known as the MSY [20]. Despite its disregard to cost, the MSY remains the main criteria for managing populations and avoiding over exploitation.
In our analysis, we focus on the maximum sustainable yield commonly known as the MSY [20]. Despite its disregard to cost, the MSY remains the main criteria for managing populations and avoiding over exploitation.
The paper is structured as follows: in Sections 2 and 3, we discuss the existence of periodic solutions and the basin of attraction of the stable periodic solution. In Section 4, we address different aspects of constant yield harvesting in periodic environment, then we focus on periodic harvesting in periodic environments and its effect on population's resonance/attenuance. We make a comparison with other harvesting strategies and give a full discussion when  Finally, we close the paper with a brief conclusion and a few questions that are worth further investigation.
Finally, we close the paper with a brief conclusion and a few questions that are worth further investigation.
2. Preliminary
In this section, we give a preliminary result that is necessary in our consequent analysis. Assume we have constant harvesting on (1.1) with periodically fluctuating carrying capacities, that is,

where  is the constant intensity of harvesting. Since when
is the constant intensity of harvesting. Since when  is a necessary condition for a population to persist, we always assume
is a necessary condition for a population to persist, we always assume  Next, define the maps
Next, define the maps  and
and  for all
for all  The orbits of (2.1) take the form
The orbits of (2.1) take the form

For each  define the matrix
define the matrix

and consider the operators  where
where  . A simple induction argument shows that orbit (2.2) takes the matrix form
. A simple induction argument shows that orbit (2.2) takes the matrix form

where  and
and  For more details about this approach, we refer the reader to [19].
For more details about this approach, we refer the reader to [19].
Proposition 2.1.
Each of the following holds true for (2.1).
-
(i)
If
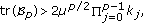 then there exist two
then there exist two 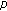 -cycles; one of them is stable and the other is unstable.
-cycles; one of them is stable and the other is unstable. -
(ii)
If
 then exactly one semistable
then exactly one semistable  -cycle exists.
-cycle exists. -
(iii)
If
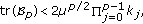 then there are no periodic solutions and consequently, no population persists.
then there are no periodic solutions and consequently, no population persists.
Proof.
It follows along the same lines as [19, Proof of Theorem  ]. Nevertheless, it is enough to observe that the cycles depend on the monotonically increasing function
]. Nevertheless, it is enough to observe that the cycles depend on the monotonically increasing function  in (2.2).
in (2.2).  has two fixed points if and only if the eigenvalues of the matrix
has two fixed points if and only if the eigenvalues of the matrix  in (2.4) are distinct real numbers. The eigenvalues of
in (2.4) are distinct real numbers. The eigenvalues of  are given by
are given by

and the radicand gives the conditions in (i), (ii), and (iii). If  are the two fixed points of
are the two fixed points of  then
then

are the two  -cycles of (2.1). Furthermore, since
-cycles of (2.1). Furthermore, since  is strictly increasing, then the positive equilibrium
is strictly increasing, then the positive equilibrium  is unstable and
is unstable and  is stable. When
is stable. When  at
at  we obtain semistability (stability from above only). Because the maps
we obtain semistability (stability from above only). Because the maps  ,
,  are continuous, then the cycles of (2.1) inherit the stability of
are continuous, then the cycles of (2.1) inherit the stability of  and
and  under the monotonic map
under the monotonic map  Finally, when
Finally, when  has no fixed points, then we have a monotonically increasing function below
has no fixed points, then we have a monotonically increasing function below  and obviously, orbits go negative in finite time.
and obviously, orbits go negative in finite time.
Proposition 2.1 shows that a constraint on  is necessary to assure the long-term survival of a population governed by (2.1). The harvesting level reaches its maximum
is necessary to assure the long-term survival of a population governed by (2.1). The harvesting level reaches its maximum  when the
when the  -cycle becomes semistable. Thus, we proceed with the assumption that
-cycle becomes semistable. Thus, we proceed with the assumption that  and
and  is the smallest positive solution of the equation
is the smallest positive solution of the equation 
3. Harvesting Levels and the Basin of Attraction
It is well known [21, 22] that for  system (2.1) has a globally asymptotically stable
system (2.1) has a globally asymptotically stable  -cycle, that is, the basin of attraction of the
-cycle, that is, the basin of attraction of the  -cycle is
-cycle is  In this section, we consider (2.1) with
In this section, we consider (2.1) with  and investigate the basin of attraction of the stable/semistable
and investigate the basin of attraction of the stable/semistable  -cycle. But first, we give a few necessary definitions. A solution of (2.1) is called persistent if the corresponding initial population survives indefinitely. Here, it is worth emphasizing that although one can start iterating (2.1) at any time
-cycle. But first, we give a few necessary definitions. A solution of (2.1) is called persistent if the corresponding initial population survives indefinitely. Here, it is worth emphasizing that although one can start iterating (2.1) at any time  time reference is crucial in our analysis, and an initial population is meant
time reference is crucial in our analysis, and an initial population is meant  all the time. A set
all the time. A set  is persistent if each solution of (2.1) with
is persistent if each solution of (2.1) with  is persistent. We refer those who are interested in reading more about persistence and its significance to [23, 24]. At a harvesting level
is persistent. We refer those who are interested in reading more about persistence and its significance to [23, 24]. At a harvesting level  let
let  be the largest persistent set, which we simply call the persistent set. Obviously, when
be the largest persistent set, which we simply call the persistent set. Obviously, when  and
and  is empty when
is empty when  Thus, a persistent set must contain the basin of attraction of the stable
Thus, a persistent set must contain the basin of attraction of the stable  -cycle assured by Proposition 2.1.
-cycle assured by Proposition 2.1.
Proposition 3.1.
Let  and let
and let  be the unstable
be the unstable  -cycle. Then
-cycle. Then 
Proof.
Since  then the map
then the map  defined in (2.2) has two fixed points, say
defined in (2.2) has two fixed points, say  and
and  where
where  Now, the other elements of the unstable cycle are given by
Now, the other elements of the unstable cycle are given by 
 Let
Let  From the monotonicity of the maps
From the monotonicity of the maps  we obtain
we obtain  for all
for all  Thus
Thus  Now, if
Now, if  then
then  and the monotonicity of
and the monotonicity of  implies
implies  For sufficiently large
For sufficiently large 
 which completes the proof.
which completes the proof.
Proposition 3.2.
Suppose that  for all
for all  and let
and let  be the fixed points of the map
be the fixed points of the map  Then,
Then,

Proof.
Since  for each
for each  then each map
then each map  has two fixed points
has two fixed points  Now, trace the iterates of (2.1) for a given initial condition
Now, trace the iterates of (2.1) for a given initial condition  to obtain the result.
to obtain the result.
If we have complete control over the carrying capacities in the  -periodic sequence
-periodic sequence  then Theorem 4.2 shows that we can achieve a maximum harvesting level by taking a constant carrying capacity, that is,
then Theorem 4.2 shows that we can achieve a maximum harvesting level by taking a constant carrying capacity, that is,  However, assume we do not have this absolute power, but we have a flexible control over the periodic permutation of the carrying capacities
However, assume we do not have this absolute power, but we have a flexible control over the periodic permutation of the carrying capacities  . In other words, we are considering a difference equation of the form
. In other words, we are considering a difference equation of the form

where  is a permutation of
is a permutation of  and
and  for all positive integers
for all positive integers  Under these circumstances, we give the next result.
Under these circumstances, we give the next result.
Theorem 3.3.
Fix a set of carrying capacities  All equations of the form (3.2) with permutations
All equations of the form (3.2) with permutations  in the dihedral group of order
in the dihedral group of order  give the same maximum constant harvesting level.
give the same maximum constant harvesting level.
Proof.
The maximum harvesting level is the smallest positive solution of the equation

Now, the elements of the dihedral group  are rotations and reflections. The rotations are assured by the trivial trace property
are rotations and reflections. The rotations are assured by the trivial trace property  For the reflections, we need to show that
For the reflections, we need to show that

First, we rewrite the matrix  in (2.3) as
in (2.3) as  where
where

By simple induction, we can show that

Now, let  be the power set of
be the power set of  We expand the product of the matrices
We expand the product of the matrices  and write
and write

where  is the cardinality of the set
is the cardinality of the set  and
and

Now, proving (3.4) is equivalent to proving that

This is obvious if  is either the empty or the complete set
is either the empty or the complete set  . If
. If  is a nonempty proper subset of
is a nonempty proper subset of  then
then  contains the product of at least one matrix
contains the product of at least one matrix  and one matrix
and one matrix  Thus, using the rotation property, we can write
Thus, using the rotation property, we can write

for some positive integers  that satisfy
that satisfy  and
and  Since
Since

then

On the other hand,

which completes the desired proof.
Next, we give the polynomials tr( ) for
) for  , whose lowest positive root gives the maximal constant harvesting level in a periodic environment, then we give an illustrative example.
, whose lowest positive root gives the maximal constant harvesting level in a periodic environment, then we give an illustrative example.

Example 3.4.
-
(i)
Consider the case

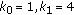 , and
, and 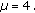 Then the value of
Then the value of  and the semistable
and the semistable  -cycle is
-cycle is 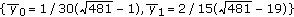 with the interval
with the interval 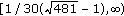 as the basin of attraction. Changing the order of the carrying capacities to
as the basin of attraction. Changing the order of the carrying capacities to 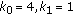 , does not change the value of
, does not change the value of 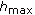 , but it does in return extend the basin of attraction to
, but it does in return extend the basin of attraction to 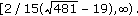 In fact, for constant harvesting in periodic environment with
In fact, for constant harvesting in periodic environment with 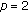 , the order of carrying capacities does not affect
, the order of carrying capacities does not affect  but
but 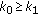 will enlarge the basin of attraction.
will enlarge the basin of attraction. -
(ii)
For
 the order of
the order of  does not change
does not change 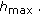 This is a little striking since in the absence of harvesting, the order of
This is a little striking since in the absence of harvesting, the order of  does change the average population. In fact, if
does change the average population. In fact, if 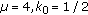 ,
,  , and
, and 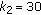 and in the absence of harvesting, the average population is
and in the absence of harvesting, the average population is 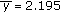 which is
which is 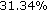 more than the average population of
more than the average population of 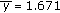 obtained if the carrying capacities were presented in the order
obtained if the carrying capacities were presented in the order 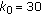 ,
, 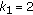 , and
, and 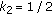 . The difference between the two populations is actually as high as
. The difference between the two populations is actually as high as 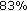 if
if  .
. -
(iii)
For
 there are 24 permutations of
there are 24 permutations of 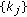 but the value of
but the value of  can only take three possible values. For each of these values, there corresponds a value of
can only take three possible values. For each of these values, there corresponds a value of  For instance, if
For instance, if  (3.15)
(3.15)
then  and their cyclic permutations give
and their cyclic permutations give 
 and their cyclic permutations give
and their cyclic permutations give  and
and  and their cyclic permutations give
and their cyclic permutations give  Notice that the difference between the two extremes is about
Notice that the difference between the two extremes is about 
The next result shows which permutation would maximize the harvesting level for some values of 
Theorem 3.5.
Consider (3.2) and assume the initial population is sufficiently large. Without loss of generality, let  Each of the following holds true.
Each of the following holds true.
-
(i)
For
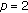 or
or 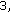 a permutation of the carrying capacities does not change the maximum harvesting level.
a permutation of the carrying capacities does not change the maximum harvesting level. -
(ii)
For
 we can achieve three different levels of maximum harvesting through permutations of the carrying capacities. In particular,
we can achieve three different levels of maximum harvesting through permutations of the carrying capacities. In particular, 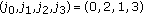 or
or 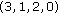 and their cyclic permutations give the largest, and
and their cyclic permutations give the largest, and  or
or  and their cyclic permutations give the smallest.
and their cyclic permutations give the smallest. -
(iii)
For
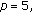 we can achieve twelve different levels of maximum harvesting through permutations of the carrying capacities. In particular,
we can achieve twelve different levels of maximum harvesting through permutations of the carrying capacities. In particular,  or
or 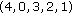 and their cyclic permutations give the largest, and
and their cyclic permutations give the largest, and  or
or 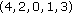 and their cyclic permutations give the smallest.
and their cyclic permutations give the smallest.
Proof.
Since the maximum harvesting level for each permutation  is achieved at
is achieved at

then we need to investigate the minimum positive value of  that satisfies this equation. (i) follows straight from the expressions of
that satisfies this equation. (i) follows straight from the expressions of  and
and  To prove (ii), classify the
To prove (ii), classify the  elements of the permutation group into three subgroups, each of which is isomorphic to the dihedral group of order 4. Now, Theorem 3.3 says that it is possible to obtain three different values of
elements of the permutation group into three subgroups, each of which is isomorphic to the dihedral group of order 4. Now, Theorem 3.3 says that it is possible to obtain three different values of  More specifically,
More specifically,  or
or  and their cyclic permutations give the same maximum harvesting level, say
and their cyclic permutations give the same maximum harvesting level, say  Similarly,
Similarly,  or
or  and their cyclic permutations give
and their cyclic permutations give 
 or
or  and their cyclic permutations give
and their cyclic permutations give  Now, we proceed to show that
Now, we proceed to show that  Define
Define

then  and
and  for
for  Furthermore, straightforward computations show that
Furthermore, straightforward computations show that

Now,  implies that
implies that  ,
,  implies that
implies that  and
and  implies that
implies that  The proof of (iii) is computational and too long; however, it follows along the same lines as the proof of (ii), and thus, we omit it.
The proof of (iii) is computational and too long; however, it follows along the same lines as the proof of (ii), and thus, we omit it.
4. Periodic Harvesting in a Periodic Environment
In this section, we consider

Observe that if  for all
for all  then we have the constant yield harvesting. Thus we discuss the constant yield harvesting first followed by the more general periodic case, then we discuss resonance and attenuance. Finally, for the sake of concreteness, we focus on the specific case
then we have the constant yield harvesting. Thus we discuss the constant yield harvesting first followed by the more general periodic case, then we discuss resonance and attenuance. Finally, for the sake of concreteness, we focus on the specific case 
4.1. Constant Yield Harvesting in a Periodic Environment
We force  in (4.1) to obtain (2.1). Observe that
in (4.1) to obtain (2.1). Observe that  is asymptotic to
is asymptotic to  So, it is obvious that
So, it is obvious that  , where
, where  is a threshold level of harvesting that needs to be investigated. The next result gives an upper bound on the maximal harvesting level
is a threshold level of harvesting that needs to be investigated. The next result gives an upper bound on the maximal harvesting level  .
.
Proposition 4.1.
Consider (2.1), then

Proof.
The set on the right-hand side of the inequality is the stable cycle at zero harvesting level.
By now, it is well known that periodic environment does not enhance populations governed by the Beverton-Holt model with constant growth rate and periodic capacity [21, 22, 25, 26]. This suggests that periodic environment has a negative impact on the maximum harvesting level. Indeed, we have the following result.
Theorem 4.2.
Consider (2.1); then the maximum harvesting level  in a periodic environment is less than the maximum harvesting level in a constant environment with
in a periodic environment is less than the maximum harvesting level in a constant environment with 
Proof.
Let  be the semistable
be the semistable  -cycle assured at the maximum harvesting level
-cycle assured at the maximum harvesting level  From (2.1), we obtain
From (2.1), we obtain

and thus

Since the map  has absolute maximum at
has absolute maximum at  then
then

The right-hand side of the inequality is the maximum harvesting level at the constant carrying capacity  which completes the proof.
which completes the proof.
4.2. The General Case
By considering the matrix of (2.3) to be

Proposition 2.1 continues to hold with the exception that cycles period may not be minimal, that is, the cycle's period could be a divisor of  This is due to the freedom in the two parameters
This is due to the freedom in the two parameters  and
and  For instance, consider
For instance, consider  and
and

In this case,  is an equilibrium point and
is an equilibrium point and  is a 4-cycle. Furthermore,
is a 4-cycle. Furthermore,  is the persistent set. For more details about the structure of periodic solutions in periodic discrete systems, we refer the reader to [27, 28].
is the persistent set. For more details about the structure of periodic solutions in periodic discrete systems, we refer the reader to [27, 28].
In a constant capacity environment with  , the maximum constant harvesting is
, the maximum constant harvesting is  . The following theorem indicates that periodic harvesting in a periodic environment gives an average harvest rate less than
. The following theorem indicates that periodic harvesting in a periodic environment gives an average harvest rate less than  .
.
Theorem 4.3.
Consider  to be the average of the maximum harvesting levels in (4.1). Then
to be the average of the maximum harvesting levels in (4.1). Then

Proof.
If (4.1) has no periodic solution, then no population persists. So, let  be a periodic solution of period
be a periodic solution of period  (not necessarily minimal). Now, use the same argument as in the proof of Theorem 4.2 to obtain the result.
(not necessarily minimal). Now, use the same argument as in the proof of Theorem 4.2 to obtain the result.
Despite the inferiority of  as shown in Theorem 4.3, one cannot underestimate the flexibility of periodic harvesting in terms of harvesting efforts and the effect on populations. Let
as shown in Theorem 4.3, one cannot underestimate the flexibility of periodic harvesting in terms of harvesting efforts and the effect on populations. Let  for all
for all  and take
and take

then  is an equilibrium of (4.1). Furthermore, when
is an equilibrium of (4.1). Furthermore, when  is unstable, that is,
is unstable, that is,

then  is the persistent set, which gives us the advantage of controlling the persistent set for the benefit of low-level populations.
is the persistent set, which gives us the advantage of controlling the persistent set for the benefit of low-level populations.
Theorems 4.2 and 4.3 along with the results of [19] prove that in order to maximize harvesting, when given a choice of environment and type of harvesting, constant harvesting in constant environment is superior. Suppose we are given a choice between two options: (1) periodically harvesting in a constant capacity environment and (2) constantly harvesting in a periodic environment. The next theorem asserts that option (1) can be better if done carefully.
Theorem 4.4.
Let  be the maximum harvesting level that can be achieved with periodic carrying capacity
be the maximum harvesting level that can be achieved with periodic carrying capacity  We can find harvesting quotas
We can find harvesting quotas  in a constant environment with
in a constant environment with  such that
such that 
Proof.
Take the maximum harvesting level  in a constant environment with
in a constant environment with  then
then  by Theorem 4.2. Now take
by Theorem 4.2. Now take  for sufficiently small
for sufficiently small  to achieve the required task.
to achieve the required task.
4.3. Resonance and Attenuance
It is well known [21, 25] that populations governed by the periodic Beverton-Holt model

exhibit attenuance, that is, the average of the stable cycle is less than the stable equilibrium in the deterministic Beverton-Holt model with carrying capacity equaling the average of the carrying capacities in (4.11). AlSharawi and Rhouma [19] also found that periodic harvesting in a deterministic environment

forces populations governed by the Beverton-Holt model to attenuate. This discussion motivates us to discuss whether populations governed by (4.1) exhibit attenuance too. Indeed, our next theorem shows that the Cushing-Henson Conjecture [21, 22, 25, 26, 29] is valid for (4.1).
Theorem 4.5.
Populations governed by (4.1) exhibit attenuance.
To simplify the proof, let us give some simple facts. For constant harvesting in a constant environment with  simple computations show that the stable (or semistable) equilibrium
simple computations show that the stable (or semistable) equilibrium  of
of

exists when  and satisfies the inequality
and satisfies the inequality

The next lemma [30] is a simple generalization of Jensen's inequality.
Lemma 4.6.
Let  be a strictly concave function, and let
be a strictly concave function, and let  be defined as
be defined as  then
then

Now, we are ready to prove Theorem 4.5.
Proof of Theorem 4.5..
If  where
where  is as defined in (2.4) and
is as defined in (2.4) and  is as defined in (4.6), then no population will persist and thus, we have trivial attenuance. So, we assume
is as defined in (4.6), then no population will persist and thus, we have trivial attenuance. So, we assume  and consider
and consider  to be the average of the stable (or semistable)
to be the average of the stable (or semistable)  -cycle (the period is not necessarily minimal) of (4.1). From (4.1), we obtain
-cycle (the period is not necessarily minimal) of (4.1). From (4.1), we obtain

Use Lemma 4.6 to obtain

Thus,  exists in (4.13) and
exists in (4.13) and

From Inequality (4.17) and (4.18), we obtain

Now, use Inequality (4.14) and the fact that  is decreasing on the interval
is decreasing on the interval  to obtain
to obtain 
4.4. The Case 
Let us focus on (4.1) with 
Lemma 4.7.
Consider periodic harvesting in a periodic environment with  Then
Then

Proof.
Solve  for
for  to obtain
to obtain

In particular, if both  and
and  are nonnegative then
are nonnegative then

Theorem 4.8.
Consider (4.1) with 
-
(i)
If
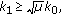 then
then 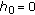 and
and 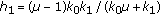 give the maximum harvesting average. Moreover, the
give the maximum harvesting average. Moreover, the  -cycle is
-cycle is 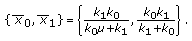 (4.23)
(4.23)
-
(ii)
If
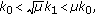 then
then 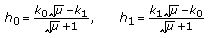 (4.24)
(4.24)give the maximum harvesting average. Moreover, the
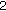 -cycle is
-cycle is (4.25)
(4.25) -
(iii)
If
 then
then 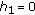 and
and 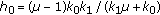 give the maximum harvesting average. Moreover, the
give the maximum harvesting average. Moreover, the 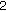 -cycle is
-cycle is 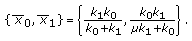 (4.26)
(4.26)Furthermore, the persistent set in each case is

Proof.
To prove (ii), use Lagrange multipliers to maximize the average of  and
and  subject to the constraint
subject to the constraint  then use the known values of
then use the known values of  and
and  to find the
to find the  -cycle. The values of
-cycle. The values of  and
and  in (i) follow from (ii) and the extra constraints on
in (i) follow from (ii) and the extra constraints on  and
and  as given in Lemma 4.7, then use the known values of
as given in Lemma 4.7, then use the known values of  and
and  to find the
to find the  -cycle. (iii) follows from (i) by swapping the order of
-cycle. (iii) follows from (i) by swapping the order of  and
and 
Next, we make comparison between the harvesting strategies.
Theorem 4.9.
Consider  and assume the initial population is sufficiently large. Periodic harvesting in a periodic environment gives larger harvesting average compared to constant harvesting in a periodic environment.
and assume the initial population is sufficiently large. Periodic harvesting in a periodic environment gives larger harvesting average compared to constant harvesting in a periodic environment.
Proof.
Consider  and solve
and solve  for
for  to find
to find

Now, compare  with the average of
with the average of  and
and  from Theorem 4.8. If
from Theorem 4.8. If  then
then  and
and  when
when

However, since

then  does not change sign for all
does not change sign for all  Furthermore, fixed values of
Furthermore, fixed values of  show that
show that  If
If  then
then  and
and  if and only if
if and only if  Assuming
Assuming  we obtain
we obtain 
Now, let us present a detailed comparison in the following illustrative examples.
Example 4.10.
Consider



The first equation is for constant harvesting in a constant environment, (4.31) is for constant harvesting in a periodic environment, and (4.32) is for periodic harvesting in a periodic environment. Notice that we are taking  in (4.30), while in both (4.31) and (4.32) and for comparison reasons, we assumed that the carrying capacities alternate periodically between the values
in (4.30), while in both (4.31) and (4.32) and for comparison reasons, we assumed that the carrying capacities alternate periodically between the values  and
and  to obtain the average
to obtain the average  . Let
. Let  ,
,  and
and  be respectively the maximal harvesting levels for equations (4.30), (4.31), and (4.32). Straightforward computations give
be respectively the maximal harvesting levels for equations (4.30), (4.31), and (4.32). Straightforward computations give

where

Example 4.11.
In each of the following cases, consider  .
.
-
(i)
Consider periodic harvesting in a periodic environment with
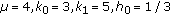 , and
, and 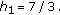 Then
Then -
(a)
the average harvesting is
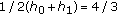 ;
; -
(b)
the
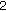 -cycle is
-cycle is 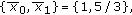 which has an average of
which has an average of 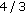 ;
; -
(c)
the persistent set is
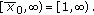
-
(a)
-
(ii)
Consider constant harvesting in a periodic environment with
 Then
Then-
(a)
The average harvesting is
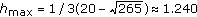 ;
; -
(b)
The
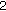 -cycle is
-cycle is (4.35)
(4.35)which has an average of
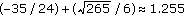 ;
; -
(c)
The persistent set is
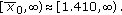
-
(a)
5. Conclusion and Discussion
In a previous paper [19], we have established that for the deterministic Beverton-Holt model, constant harvesting is superior to both periodic and conditional harvestings when the maximum sustainable yield is taken as the management objective, and when the initial population is sufficiently large. In this paper, we obtained the following.
-
(i)
Constant harvesting in a constant environment is "better" than constant harvesting in a periodic environment (Theorem 4.2 ).
-
(ii)
Constant harvesting in a constant environment is "better" than periodic harvesting in a periodic environment (Theorem 4.3 ). However, at least in the case
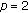 and for some range of the parameters, careful periodic harvesting can lead to the same yield as the optimal constant harvesting.
and for some range of the parameters, careful periodic harvesting can lead to the same yield as the optimal constant harvesting. -
(iii)
Periodic harvesting in a periodic environment is "better" than constant harvesting in a periodic environment.
Finally, this study left us with few questions that deserve further investigations.
Question 1.
Fix a set of carrying capacities  and consider all permutations of
and consider all permutations of  in (3.2). According to the Theorem 3.3, we obtain
in (3.2). According to the Theorem 3.3, we obtain  values for
values for  and Theorem 3.5 characterizes those values for
and Theorem 3.5 characterizes those values for  , and
, and  Complete the characterization for general
Complete the characterization for general 
Question 2.
Consider (4.1) and let  be a set of harvesting quotas that give a nonempty persistent set. Which permutation of
be a set of harvesting quotas that give a nonempty persistent set. Which permutation of  would enlarge the persistent set?
would enlarge the persistent set?
Question 3.
Generalize the results of this study to the case where the inheritance growth rate  is nonconstant.
is nonconstant.
References
Kelleher K, Willmann R, Arnason R: The Sunken Billions, the Economic Justification for Fisheries Reform. The World Bank, Washington, DC, USA; 2009.
Azar C, Holmberg J, Lindgren K: Stability analysis of harvesting in a predator-prey model. Journal of Theoretical Biology 1995,174(1):13-19. 10.1006/jtbi.1995.0076
Brauer F, Soudack AC: Stability regions and transition phenomena for harvested predator-prey systems. Journal of Mathematical Biology 1979,7(4):319-337. 10.1007/BF00275152
Brauer F, Soudack AC: Stability regions in predator-prey systems with constant-rate prey harvesting. Journal of Mathematical Biology 1979,8(1):55-71. 10.1007/BF00280586
Dai G, Tang M: Coexistence region and global dynamics of a harvested predator-prey system. SIAM Journal on Applied Mathematics 1998,58(1):193-210. 10.1137/S0036139994275799
Myerscough MR, Gray BF, Hogarth WL, Norbury J: An analysis of an ordinary differential equation model for a two-species predator-prey system with harvesting and stocking. Journal of Mathematical Biology 1992,30(4):389-411. 10.1007/BF00173294
Xiao D, Ruan S: Bogdanov-Takens bifurcations in predator-prey systems with constant rate harvesting. In Differential Equations with Applications to Biology (Halifax, NS, 1997), Fields Institute Communications. Volume 21. American Mathematical Society, Providence, RI, USA; 1999:493-506.
Tang S, Chen L: The effect of seasonal harvesting on stage-structured population models. Journal of Mathematical Biology 2004,48(4):357-374. 10.1007/s00285-003-0243-5
Xiao Y, Cheng D, Qin H: Optimal impulsive control in periodic ecosystem. Systems & Control Letters 2006,55(7):558-565. 10.1016/j.sysconle.2005.12.003
Zhang X, Shuai Z, Wang K: Optimal impulsive harvesting policy for single population. Nonlinear Analysis: Real World Applications 2003,4(4):639-651. 10.1016/S1468-1218(02)00084-6
Braverman E, Mamdani R: Continuous versus pulse harvesting for population models in constant and variable environment. Journal of Mathematical Biology 2008,57(3):413-434. 10.1007/s00285-008-0169-z
Ludwig D: Harvesting strategies for a randomly fluctuating population. Journal du Conseil pour l'Exploration de La Mer 1980, 39: 168-174.
Xu C, Boyce MS, Daley DJ: Harvesting in seasonal environments. Journal of Mathematical Biology 2005,50(6):663-682. 10.1007/s00285-004-0303-5
Sinha S, Parthasarathy S: Unusual dynamics of extinction in a simple ecological model. Proceedings of the National Academy of Sciences of the United States of America 1996,93(4):1504-1508. 10.1073/pnas.93.4.1504
Chau NP: Destabilising effect of periodic harvest on population dynamics. Ecological Modelling 2000,127(1):1-9. 10.1016/S0304-3800(99)00190-8
Berezansky L, Braverman E: On impulsive Beverton-Holt difference equations and their applications. Journal of Difference Equations and Applications 2004,10(9):851-868. 10.1080/10236190410001726421
Tang S, Cheke RA, Xiao Y: Optimal implusive harvesting on non-autonomous Beverton-Holt difference equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(12):2311-2341. 10.1016/j.na.2006.02.049
AlSharawi Z, Rhouma M: Coexistence and extinction in a competitive exclusion Leslie/Gower model with harvesting and stocking. Journal of Difference Equations and Applications 2009,15(11-12):1031-1053. 10.1080/10236190802459861
AlSharawi Z, Rhouma M: The Beverton-Holt model with periodic and conditional harvesting. Journal of Biological Dynamics 2009, 3: 463-478. 10.1080/17513750802601041
Clark CW: Mathematical Bioeconomics, the Optimal Management of Renewable Resources, Pure and Applied Mathematics. 2nd edition. John Wiley & Sons, New York, NY, USA; 1990:xiv+386.
Cushing JM, Henson SM: A periodically forced Beverton-Holt equation. Journal of Difference Equations and Applications 1998,58(12):193-210.
Elaydi S, Sacker RJ: Nonautonomous Beverton-Holt equations and the Cushing-Henson conjectures. Journal of Difference Equations and Applications 2005,11(4-5):337-346. 10.1080/10236190412331335418
Schreiber SJ: Allee effects, extinctions, and chaotic transients in simple population models. Theoretical Population Biology 2003,64(2):201-209. 10.1016/S0040-5809(03)00072-8
Schreiber SJ: Chaos and population disappearances in simple ecological models. Journal of Mathematical Biology 2001,42(3):239-260. 10.1007/s002850000070
Cushing JM, Henson SM: Global dynamics of some periodically forced, monotone difference equations. Journal of Difference Equations and Applications 2001,7(6):859-872. 10.1080/10236190108808308
Kocic VL: A note on the nonautonomous Beverton-Holt model. Journal of Difference Equations and Applications 2005,11(4-5):415-422. 10.1080/10236190412331335463
AlSharawi Z: Periodic orbits in periodic discrete dynamics. Computers & Mathematics with Applications 2008,56(8):1966-1974. 10.1016/j.camwa.2008.04.020
AlSharawi Z, Angelos J, Elaydi S, Rakesh L: An extension of Sharkovsky's theorem to periodic difference equations. Journal of Mathematical Analysis and Applications 2006,316(1):128-141. 10.1016/j.jmaa.2005.04.059
Braverman E, Saker SH: On the Cushing-Henson conjecture, delay difference equations and attenuant cycles. Journal of Difference Equations and Applications 2008,14(3):275-286. 10.1080/10236190701565511
Woeginger G: When Cauchy and Holder met Minkowski: a tour through well-known inequalities. Mathematics Magazine 2009, 82: 202-207. 10.4169/193009809X468814
Acknowledgments
The authors would like to thank the anonymous referee for his/her valuable suggestions. This work is supported by SQU internal Grant DVC/PSR/2009/36.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
AlSharawi, Z., Ben Haj Rhouma, M. The Discrete Beverton-Holt Model with Periodic Harvesting in a Periodically Fluctuating Environment. Adv Differ Equ 2010, 215875 (2010). https://doi.org/10.1155/2010/215875
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/215875
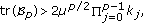 then there exist two
then there exist two 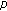 -cycles; one of them is stable and the other is unstable.
-cycles; one of them is stable and the other is unstable. then exactly one semistable
then exactly one semistable  -cycle exists.
-cycle exists.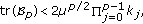 then there are no periodic solutions and consequently, no population persists.
then there are no periodic solutions and consequently, no population persists.
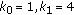 , and
, and 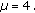 Then the value of
Then the value of  and the semistable
and the semistable  -cycle is
-cycle is 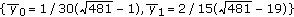 with the interval
with the interval 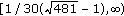 as the basin of attraction. Changing the order of the carrying capacities to
as the basin of attraction. Changing the order of the carrying capacities to 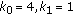 , does not change the value of
, does not change the value of 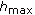 , but it does in return extend the basin of attraction to
, but it does in return extend the basin of attraction to 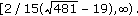 In fact, for constant harvesting in periodic environment with
In fact, for constant harvesting in periodic environment with 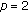 , the order of carrying capacities does not affect
, the order of carrying capacities does not affect  but
but 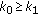 will enlarge the basin of attraction.
will enlarge the basin of attraction. the order of
the order of  does not change
does not change 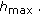 This is a little striking since in the absence of harvesting, the order of
This is a little striking since in the absence of harvesting, the order of  does change the average population. In fact, if
does change the average population. In fact, if 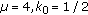 ,
,  , and
, and 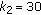 and in the absence of harvesting, the average population is
and in the absence of harvesting, the average population is 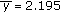 which is
which is 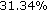 more than the average population of
more than the average population of 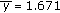 obtained if the carrying capacities were presented in the order
obtained if the carrying capacities were presented in the order 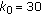 ,
, 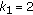 , and
, and 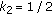 . The difference between the two populations is actually as high as
. The difference between the two populations is actually as high as 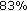 if
if  .
. there are 24 permutations of
there are 24 permutations of 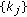 but the value of
but the value of  can only take three possible values. For each of these values, there corresponds a value of
can only take three possible values. For each of these values, there corresponds a value of  For instance, if
For instance, if 
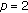 or
or 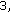 a permutation of the carrying capacities does not change the maximum harvesting level.
a permutation of the carrying capacities does not change the maximum harvesting level. we can achieve three different levels of maximum harvesting through permutations of the carrying capacities. In particular,
we can achieve three different levels of maximum harvesting through permutations of the carrying capacities. In particular, 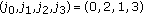 or
or 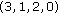 and their cyclic permutations give the largest, and
and their cyclic permutations give the largest, and  or
or  and their cyclic permutations give the smallest.
and their cyclic permutations give the smallest.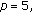 we can achieve twelve different levels of maximum harvesting through permutations of the carrying capacities. In particular,
we can achieve twelve different levels of maximum harvesting through permutations of the carrying capacities. In particular,  or
or 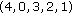 and their cyclic permutations give the largest, and
and their cyclic permutations give the largest, and  or
or 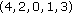 and their cyclic permutations give the smallest.
and their cyclic permutations give the smallest.
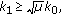 then
then 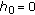 and
and 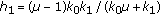 give the maximum harvesting average. Moreover, the
give the maximum harvesting average. Moreover, the  -cycle is
-cycle is 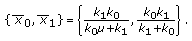
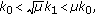 then
then 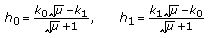
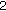 -cycle is
-cycle is
 then
then 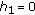 and
and 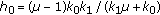 give the maximum harvesting average. Moreover, the
give the maximum harvesting average. Moreover, the 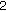 -cycle is
-cycle is 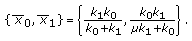

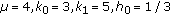 , and
, and 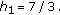 Then
Then 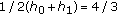 ;
;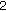 -cycle is
-cycle is 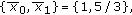 which has an average of
which has an average of 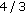 ;
;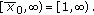
 Then
Then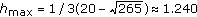 ;
;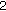 -cycle is
-cycle is
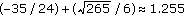 ;
;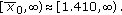
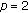 and for some range of the parameters, careful periodic harvesting can lead to the same yield as the optimal constant harvesting.
and for some range of the parameters, careful periodic harvesting can lead to the same yield as the optimal constant harvesting.