- Research Article
- Open access
- Published:
Existence of Nonoscillatory Solutions to Second-Order Neutral Delay Dynamic Equations on Time Scales
Advances in Difference Equations volume 2009, Article number: 562329 (2009)
Abstract
We employ Kranoselskii's fixed point theorem to establish the existence of nonoscillatory solutions to the second-order neutral delay dynamic equation  on a time scale T. To dwell upon the importance of our results, one interesting example is also included.
on a time scale T. To dwell upon the importance of our results, one interesting example is also included.
1. Introduction
The theory of time scales, which has recently received a lot of attention, was introduced by Hilger in his Ph.D. Thesis in 1988 in order to unify continuous and discrete analysis (see Hilger [1]). Several authors have expounded on various aspects of this new theory; see the survey paper by Agarwal et al. [2] and references cited therein. A book on the subject of time scales, by Bohner and Peterson [3], summarizes and organizes much of the time scale calculus; we refer also to the last book by Bohner and Peterson [4] for advances in dynamic equations on time scales. For the notation used below we refer to the next section that provides some basic facts on time scales extracted from Bohner and Peterson [3].
In recent years, there has been much research activity concerning the oscillation of solutions of various equations on time scales, and we refer the reader to Erbe [5], Saker [6], and Hassan [7]. And there are some results dealing with the oscillation of the solutions of second-order delay dynamic equations on time scales [8–22].
In this work, we will consider the existence of nonoscillatory solutions to the second-order neutral delay dynamic equation of the form

on a time scale  (an arbitrary closed subset of the reals).
(an arbitrary closed subset of the reals).
The motivation originates from Kulenović and Hadžiomerpahić [23] and Zhu and Wang [24]. In [23], the authors established some sufficient conditions for the existence of positive solutions of the delay equation

Recently, [24] established the existence of nonoscillatory solutions to the neutral equation

on a time scale 
Neutral equations find numerous applications in natural science and technology. For instance, they are frequently used for the study of distributed networks containing lossless transmission lines. So, we try to establish some sufficient conditions for the existence of equations of (1.1). However, there are few papers to discuss the existence of nonoscillatory solutions for neutral delay dynamic equations on time scales.
Since we are interested in the nonoscillatory behavior of (1.1), we assume throughout that the time scale  under consideration satisfies
under consideration satisfies  and
and 
As usual, by a solution of (1.1) we mean a continuous function  which is defined on
which is defined on  and satisfies (1.1) for
and satisfies (1.1) for  A solution of (1.1) is said to be eventually positive (or eventually negative) if there exists
A solution of (1.1) is said to be eventually positive (or eventually negative) if there exists  such that
such that  (or
(or  ) for all
) for all  in
in  A solution of (1.1) is said to be nonoscillatory if it is either eventually positive or eventually negative; otherwise, it is oscillatory.
A solution of (1.1) is said to be nonoscillatory if it is either eventually positive or eventually negative; otherwise, it is oscillatory.
2. Main Results
In this section, we establish the existence of nonoscillatory solutions to (1.1). For  let
let  and
and  Further, let
Further, let  denote all continuous functions mapping
denote all continuous functions mapping  into
into  and
and

Endowed on  with the norm
with the norm  (
( ) is a Banach space (see [24]). Let
) is a Banach space (see [24]). Let  we say that
we say that  is uniformly Cauchy if for any given
is uniformly Cauchy if for any given  there exists
there exists  such that for any
such that for any  for all
for all  .
.
 is said to be equicontinuous on
is said to be equicontinuous on  if for any given
if for any given  there exists
there exists  such that for any
such that for any  and
and  with
with 
Also, we need the following auxiliary results.
Lemma 2.1 (see [24, Lemma  ]).
]).
Suppose that  is bounded and uniformly Cauchy. Further, suppose that
is bounded and uniformly Cauchy. Further, suppose that  is equicontinuous on
is equicontinuous on  for any
for any  Then
Then  is relatively compact.
is relatively compact.
Lemma 2.2 (see [25, Kranoselskii's fixed point theorem]).
Suppose that  is a Banach space and
is a Banach space and  is a bounded, convex, and closed subset of
is a bounded, convex, and closed subset of  Suppose further that there exist two operators
Suppose further that there exist two operators  such that
such that
-
(i)
 for all
for all 
-
(ii)
 is a contraction mapping;
is a contraction mapping; -
(iii)
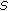 is completely continuous.
is completely continuous.
Then  has a fixed point in
has a fixed point in 
Throughout this section, we will assume in (1.1) that
 ,
,  ,
,  =
=  ,
,  =
=  ,
,  ,
, ,
,  ,
,  ,
,  =
=  , and there exists a function
, and there exists a function  such that
such that  =
=  ,
,  =
= 
Theorem 2.3.
Assume that  holds and
holds and  Then (1.1) has an eventually positive solution.
Then (1.1) has an eventually positive solution.
Proof.
From the assumption  we can choose
we can choose  large enough and positive constants
large enough and positive constants  and
and  which satisfy the condition
which satisfy the condition

such that





Furthermore, from  we see that there exists
we see that there exists  with
with  such that
such that  for
for 
Define the Banach space  as in (2.1) and let
as in (2.1) and let

It is easy to verify that  is a bounded, convex, and closed subset of
is a bounded, convex, and closed subset of 
Now we define two operators  and
and  as follows:
as follows:

Next, we will show that  and
and  satisfy the conditions in Lemma 2.2.
satisfy the conditions in Lemma 2.2.
 We first prove that
We first prove that  for any
for any  Note that for any
Note that for any  For any
For any  and
and  in view of (2.3), (2.4) and (2.6), we have
in view of (2.3), (2.4) and (2.6), we have

Similarly, we can prove that  for any
for any  and
and  Hence,
Hence,  for any
for any 
-
(ii)
We prove that
 is a contraction mapping. Indeed, for
is a contraction mapping. Indeed, for  we have
we have 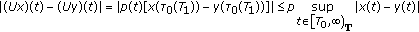 (2.10)
(2.10)
for  and
and

for  Therefore, we have
Therefore, we have

for any  Hence,
Hence,  is a contraction mapping.
is a contraction mapping.
 We will prove that
We will prove that  is a completely continuous mapping. First, by
is a completely continuous mapping. First, by  we know that
we know that  maps
maps  into
into 
Second, we consider the continuity of  Let
Let  and
and  as
as  then
then  and
and  as
as  for any
for any  Consequently, by (2.5) we have
Consequently, by (2.5) we have

for  So, we obtain
So, we obtain

which proves that  is continuous on
is continuous on 
Finally, we prove that  is relatively compact. It is sufficient to verify that
is relatively compact. It is sufficient to verify that  satisfies all conditions in Lemma 2.1. By the definition of
satisfies all conditions in Lemma 2.1. By the definition of  we see that
we see that  is bounded. For any
is bounded. For any  take
take  so that
so that

For any  and
and  we have
we have

Thus,  is uniformly Cauchy.
is uniformly Cauchy.
The remainder is to consider the equicontinuous on  for any
for any  Without loss of generality, we set
Without loss of generality, we set  For any
For any  we have
we have  for
for  and
and

for 
Now, we see that for any  there exists
there exists  such that when
such that when  with
with 

for all  This means that
This means that  is equicontinuous on
is equicontinuous on  for any
for any 
By means of Lemma 2.1,  is relatively compact. From the above, we have proved that
is relatively compact. From the above, we have proved that  is a completely continuous mapping.
is a completely continuous mapping.
By Lemma 2.2, there exists  such that
such that  Therefore, we have
Therefore, we have

which implies that  is an eventually positive solution of (1.1). The proof is complete.
is an eventually positive solution of (1.1). The proof is complete.
Theorem 2.4.
Assume that  holds and
holds and  Then (1.1) has an eventually positive solution.
Then (1.1) has an eventually positive solution.
Proof.
From the assumption  we can choose
we can choose  large enough and positive constants
large enough and positive constants  and
and  which satisfy the condition
which satisfy the condition

such that

Furthermore, from  we see that there exists
we see that there exists  with
with  such that
such that  for
for 
Define the Banach space  as in (2.1) and let
as in (2.1) and let

It is easy to verify that  is a bounded, convex, and closed subset of
is a bounded, convex, and closed subset of 
Now we define two operators  and
and  as in Theorem 2.3 with
as in Theorem 2.3 with  replaced by
replaced by  The rest of the proof is similar to that of Theorem 2.3 and hence omitted. The proof is complete.
The rest of the proof is similar to that of Theorem 2.3 and hence omitted. The proof is complete.
Theorem 2.5.
Assume that  holds and
holds and  Then (1.1) has an eventually positive solution.
Then (1.1) has an eventually positive solution.
Proof.
From the assumption  we can choose
we can choose  large enough and positive constants
large enough and positive constants  and
and  which satisfy the condition
which satisfy the condition

such that

Furthermore, from  we see that there exists
we see that there exists  with
with  such that
such that  for
for 
Define the Banach space  as in (2.1) and let
as in (2.1) and let

It is easy to verify that  is a bounded, convex, and closed subset of
is a bounded, convex, and closed subset of 
Now we define two operators  and
and  as in Theorem 2.3 with
as in Theorem 2.3 with  replaced by
replaced by  The rest of the proof is similar to that of Theorem 2.3 and hence omitted. The proof is complete.
The rest of the proof is similar to that of Theorem 2.3 and hence omitted. The proof is complete.
We will give the following example to illustrate our main results.
Example 2.6.
Consider the second-order delay dynamic equations on time scales

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  Then
Then  ,
,  ,
,  Let
Let  It is easy to see that the assumption
It is easy to see that the assumption  holds. By Theorem 2.3, (2.26) has an eventually positive solution.
holds. By Theorem 2.3, (2.26) has an eventually positive solution.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Agarwal R, Bohner M, O'Regan D, Peterson A: Dynamic equations on time scales: a survey. Journal of Computational and Applied Mathematics 2002,141(1-2):1-26. 10.1016/S0377-0427(01)00432-0
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Application. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Erbe L: Oscillation results for second-order linear equations on a time scale. Journal of Difference Equations and Applications 2002,8(11):1061-1071. 10.1080/10236190290015317
Saker SH: Oscillation criteria of second-order half-linear dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,177(2):375-387. 10.1016/j.cam.2004.09.028
Hassan TS: Oscillation criteria for half-linear dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2008,345(1):176-185. 10.1016/j.jmaa.2008.04.019
Agarwal RP, Bohner M, Saker SH: Oscillation of second order delay dynamic equations. The Canadian Applied Mathematics Quarterly 2005,13(1):1-17.
Zhang BG, Shanliang Z: Oscillation of second-order nonlinear delay dynamic equations on time scales. Computers & Mathematics with Applications 2005,49(4):599-609. 10.1016/j.camwa.2004.04.038
Şahiner Y: Oscillation of second-order delay differential equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):e1073-e1080.
Erbe L, Peterson A, Saker SH: Oscillation criteria for second-order nonlinear delay dynamic equations. Journal of Mathematical Analysis and Applications 2007,333(1):505-522. 10.1016/j.jmaa.2006.10.055
Han Z, Sun S, Shi B: Oscillation criteria for a class of second-order Emden-Fowler delay dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2007,334(2):847-858. 10.1016/j.jmaa.2007.01.004
Han Z, Shi B, Sun S: Oscillation criteria for second-order delay dynamic equations on time scales. Advances in Difference Equations 2007, 2007:-16.
Han Z, Shi B, Sun S-R: Oscillation of second-order delay dynamic equations on time scales. Acta Scientiarum Naturalium Universitatis Sunyatseni 2007,46(6):10-13.
Sun S-R, Han Z, Zhang C-H: Oscillation criteria of second-order Emden-Fowler neutral delay dynamic equations on time scales. Journal of Shanghai Jiaotong University 2008,42(12):2070-2075.
Zhang M, Sun S, Han Z:Existence of positive solutions for multipoint boundary value problem with
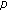 -Laplacian on time scales. Advances in Difference Equations 2009, 2009:-18.
-Laplacian on time scales. Advances in Difference Equations 2009, 2009:-18.Han Z, Li T, Sun S, Zhang C: Oscillation for second-order nonlinear delay dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-13.
Sun S, Han Z, Zhang C: Oscillation of second-order delay dynamic equations on time scales. Journal of Applied Mathematics and Computing 2009,30(1-2):459-468. 10.1007/s12190-008-0185-6
Zhao Y, Sun S: Research on Sturm-Liouville eigenvalue problems. Journal of University of Jinan 2009,23(3):299-301.
Li T, Han Z: Oscillation of certain second-order neutral difference equation with oscillating coefficient. Journal of University of Jinan 2009,23(4):410-413.
Chen W, Han Z: Asymptotic behavior of several classes of differential equations. Journal of University of Jinan 2009,23(3):296-298.
Li T, Han Z, Sun S: Oscillation of one kind of second-order delay dynamic equations on time scales. Journal of Jishou University 2009,30(3):24-27.
Kulenović MRS, Hadžiomerspahić S: Existence of nonoscillatory solution of second order linear neutral delay equation. Journal of Mathematical Analysis and Applications 1998,228(2):436-448. 10.1006/jmaa.1997.6156
Zhu Z-Q, Wang Q-R: Existence of nonoscillatory solutions to neutral dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2007,335(2):751-762. 10.1016/j.jmaa.2007.02.008
Chen YS:Existence of nonoscillatory solutions of
 th order neutral delay differential equations. Funkcialaj Ekvacioj 1992,35(3):557-570.
th order neutral delay differential equations. Funkcialaj Ekvacioj 1992,35(3):557-570.
Acknowledgments
The authors sincerely thank the reviewers for their valuable suggestions and useful comments that have lead to the present improved version of the original manuscript. This research is supported by the Natural Science Foundation of China (60774004), China Postdoctoral Science Foundation Funded Project (20080441126), Shandong Postdoctoral Funded Project (200802018), Shandong Research Funds (Y2008A28, Y2007A27), and also supported by the University of Jinan Research Funds for Doctors (B0621, XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, T., Han, Z., Sun, S. et al. Existence of Nonoscillatory Solutions to Second-Order Neutral Delay Dynamic Equations on Time Scales. Adv Differ Equ 2009, 562329 (2009). https://doi.org/10.1155/2009/562329
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/562329
 for all
for all 
 is a contraction mapping;
is a contraction mapping;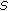 is completely continuous.
is completely continuous. is a contraction mapping. Indeed, for
is a contraction mapping. Indeed, for  we have
we have 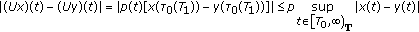
 -Laplacian on time scales. Advances in Difference Equations 2009, 2009:-18.
-Laplacian on time scales. Advances in Difference Equations 2009, 2009:-18. th order neutral delay differential equations. Funkcialaj Ekvacioj 1992,35(3):557-570.
th order neutral delay differential equations. Funkcialaj Ekvacioj 1992,35(3):557-570.