- Research Article
- Open access
- Published:
Dynamic Analysis of Stochastic Reaction-Diffusion Cohen-Grossberg Neural Networks with Delays
Advances in Difference Equations volume 2009, Article number: 410823 (2009)
Abstract
Stochastic effects on convergence dynamics of reaction-diffusion Cohen-Grossberg neural networks (CGNNs) with delays are studied. By utilizing Poincaré inequality, constructing suitable Lyapunov functionals, and employing the method of stochastic analysis and nonnegative semimartingale convergence theorem, some sufficient conditions ensuring almost sure exponential stability and mean square exponential stability are derived. Diffusion term has played an important role in the sufficient conditions, which is a preeminent feature that distinguishes the present research from the previous. Two numerical examples and comparison are given to illustrate our results.
1. Introduction
In the recent years, the problems of stability of delayed neural networks have received much attention due to its potential application in associative memories, pattern recognition and optimization. A large number of results have appeared in literature, see, for example, [1–14]. As is well known, a real system is usually affected by external perturbations which in many cases are of great uncertainty and hence may be treated as random [15–17]. As pointed out by Haykin [18] that in real nervous systems synaptic transmission is a noisy process brought on by random fluctuations from the release of neurotransmitters and other probabilistic causes, it is of significant importance to consider stochastic effects for neural networks. In recent years, the dynamic behavior of stochastic neural networks, especially the stability of stochastic neural networks, has become a hot study topic. Many interesting results on stochastic effects to the stability of delayed neural networks have been reported (see [16–23]).
In the factual operations, on other hand, diffusion phenomena could not be ignored in neural networks and electric circuits once electrons transport in a nonuniform electromagnetic field. Thus, it is essential to consider state variables varying with time and space variables. The delayed neural networks with diffusion terms can commonly be expressed by partial functional differential equation (PFDE). To study the stability of delayed reaction-diffusion neural networks, for instance, see [24–31], and references therein.
Based on the above discussion, it is significant and of prime importance to consider the stochastic effects on the stability property of the delayed reaction-diffusion networks. Recently, Sun et al. [32, 33] have studied the problem of the almost sure exponential stability and the moment exponential stability of an equilibrium solution for stochastic reaction-diffusion recurrent neural networks with continuously distributed delays and constant delays, respectively. Wan et al. have derived the sufficient condition of exponential stability of stochastic reaction-diffusion CGNNs with delay [34, 35]. In [36], the problem of stochastic exponential stability of the delayed reaction-diffusion recurrent neural networks with Markovian jumping parameters have been investigated. In [32–36], unfortunately, reaction-diffusion terms were omitted in the deductions, which result in that the criteria of obtained stability do not contain the diffusion terms. In other words, the diffusion terms do not take effect in their results. The same cases appear also in other research literatures on the stability of reaction-diffusion neural network [24–31].
Motivated by the above discussions, in this paper, we will further investigate the convergence dynamics of stochastic reaction-diffusion CGNNs with delays, where the activation functions are not necessarily bounded, monotonic, and differentiable. Utilizing Poincaré inequality and constructing appropriate Lyapunov functionals, some sufficient conditions on the almost surely and mean square exponential stability for the equilibrium point are established. The results show that diffusion terms have contributed to the almost surely and mean square exponential stability criteria. Two examples have been provided to illustrate the effectiveness of the obtained results.
The rest of this paper is organized as follows. In Section 2, a stochastic delayed reaction-diffusion CGNNs model is described, and some preliminaries are given. In Section 3, some sufficient conditions to guarantee the mean square and almost surely exponential stability of equilibrium point for the reaction-diffusion delayed CGNNs are derived. Examples and comparisons are given in Section 4. Finally, in Section 5, conclusions are given.
2. Model Description and Preliminaries
To begin with, we introduce some notations and recall some basic definitions and lemmas:
-
(i)
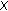 be an open bounded domain in
be an open bounded domain in 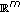 with smooth boundary
with smooth boundary 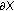 , and
, and  denotes the measure of
denotes the measure of  .
.  ;
; -
(ii)
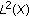 is the space of real Lebesgue measurable functions on
is the space of real Lebesgue measurable functions on 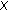 which is a Banach space for the
which is a Banach space for the 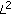 -norm
-norm 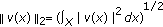 ,
, 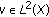 ;
; -
(iii)
 , where
, where 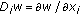 ,
, 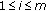 .
.  the closure of
the closure of  in
in 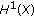 ;
; -
(iv)
 is the space of continuous functions which map
is the space of continuous functions which map  into
into  with the norm
with the norm  , for any
, for any  ;
; -
(v)
 and be an
and be an 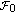 -measurable
-measurable 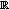 -valued random variable, where, for example,
-valued random variable, where, for example,  restricted on
restricted on 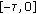 , and
, and  be the Banach space of continuous and bounded functions with the norm
be the Banach space of continuous and bounded functions with the norm  , where
, where 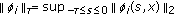 , for any
, for any  ,
,  ;
; -
(vi)
 is the gradient operator, for
is the gradient operator, for 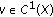 .
.  .
. 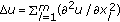 is the Laplace operator, for
is the Laplace operator, for  .
.
Consider the following stochastic reaction-diffusion CGNNs with constant delays on  :
:

where  ,
,  corresponds to the number of units in a neural network;
corresponds to the number of units in a neural network;  is a space variable,
is a space variable,  corresponds to the state of the
corresponds to the state of the  th unit at time
th unit at time  and in space
and in space  ;
;  corresponds to the transmission diffusion coefficient along the
corresponds to the transmission diffusion coefficient along the  th neuron;
th neuron;  represents an amplification function;
represents an amplification function;  is an appropriately behavior function;
is an appropriately behavior function;  ,
,  denote the connection strengths of the
denote the connection strengths of the  th neuron on the
th neuron on the  th neuron, respectively;
th neuron, respectively;  ,
,  denote the activation functions of
denote the activation functions of  th neuron at time
th neuron at time  and in space
and in space  ;
;  corresponds to the transmission delay and satisfies
corresponds to the transmission delay and satisfies  (
( is a positive constant);
is a positive constant);  is the constant input from outside of the network. Moreover,
is the constant input from outside of the network. Moreover,  is an
is an  -dimensional Brownian motion defined on a complete probability space
-dimensional Brownian motion defined on a complete probability space  with the natural filtration
with the natural filtration  generated by the process
generated by the process  , where we associate
, where we associate  with the canonical space generated by all
with the canonical space generated by all  , and denote by
, and denote by  the associated
the associated  -algebra generated by
-algebra generated by  with the probability measure
with the probability measure  . The boundary condition is given by
. The boundary condition is given by  (Dirichlet type) or
(Dirichlet type) or  (Neumann type), where
(Neumann type), where  denotes the outward normal derivative on
denotes the outward normal derivative on  .
.
Model (2.1) includes the following reaction-diffusion recurrent neural networks (RNNs) as a special case:

for  .
.
When  for any
for any  , model (2.1) also comprises the following reaction-diffusion CGNNs with no stochastic effects on space
, model (2.1) also comprises the following reaction-diffusion CGNNs with no stochastic effects on space  :
:

for  .
.
Throughout this paper, we assume that
-
(H1)
each function
 is bounded, positive and continuous, that is, there exist constants
is bounded, positive and continuous, that is, there exist constants  ,
, 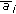 such that
such that 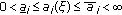 , for
, for 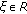 ,
, 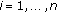 ,
, -
(H2)
 and
and  , for
, for 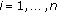 ,
, -
(H3)
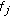 ,
, 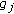 are bounded, and
are bounded, and  ,
, 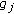 ,
, 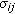 are Lipschitz continuous with Lipschitz constant
are Lipschitz continuous with Lipschitz constant  ,
, 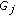 ,
, 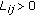 , for
, for 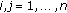 ,
, -
(H4)
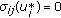 , for
, for  .
.
Using the similar method of [25], it is easily to prove that under assumptions (H1)–(H3), model (2.3) has a unique equilibrium point  which satisfies
which satisfies

Suppose that system (2.1) satisfies assumptions (H1)–(H4), then equilibrium point  of model (2.3) is also a unique equilibrium point of system (2.1).
of model (2.3) is also a unique equilibrium point of system (2.1).
By the theory of stochastic differential equations, see [15, 37], it is known that under the conditions (H1)–(H4), model (2.1) has a global solution denoted by  or simply
or simply  ,
,  or
or  , if no confusion should occur. For the effects of stochastic forces to the stability property of delayed CGNNs model (2.1), we will study the almost sure exponential stability and the mean square exponential stability of their equilibrium solution
, if no confusion should occur. For the effects of stochastic forces to the stability property of delayed CGNNs model (2.1), we will study the almost sure exponential stability and the mean square exponential stability of their equilibrium solution  in the following sections. For completeness, we give the following definitions [33], in which
in the following sections. For completeness, we give the following definitions [33], in which  denotes expectation with respect to
denotes expectation with respect to  .
.
Definition 2.1.
The equilibrium solution  of model (2.1) is said to be almost surely exponentially stable, if there exists a positive constant
of model (2.1) is said to be almost surely exponentially stable, if there exists a positive constant  such that for any
such that for any  there is a finite positive random variable
there is a finite positive random variable  such that
such that

Definition 2.2.
The equilibrium solution  of model (2.1) is said to be
of model (2.1) is said to be  th moment exponentially stable, if there exists a pair of positive constants
th moment exponentially stable, if there exists a pair of positive constants  and
and  such that for any
such that for any  ,
,

When  and
and  , it is usually called the exponential stability in mean value and mean square, respectively.
, it is usually called the exponential stability in mean value and mean square, respectively.
The following lemmas are important in our approach.
Lemma 2.3 (nonnegative semimartingale convergence theorem [16]).
Suppose  and
and  are two continuous adapted increasing processes on
are two continuous adapted increasing processes on  with
with  , a.s. Let
, a.s. Let  be a real-valued continuous local martingale with
be a real-valued continuous local martingale with  , a.s. and let
, a.s. and let  be a nonnegative
be a nonnegative  -measurable random variable with
-measurable random variable with  . Define
. Define  for
for  . If
. If  is nonnegative, then
is nonnegative, then

where  a.s. denotes
a.s. denotes  . In particular, if
. In particular, if  a.s., then for almost all
a.s., then for almost all 
 and
and  , that is, both
, that is, both  and
and  converge to finite random variables.
converge to finite random variables.
Lemma 2.4 (Poincaré inequality).
Let  be a bounded domain of
be a bounded domain of  with a smooth boundary
with a smooth boundary  of class
of class  by
by  .
.  is a real-valued function belonging to
is a real-valued function belonging to  and satisfies
and satisfies  . Then
. Then

which  is the lowest positive eigenvalue of the boundary value problem
is the lowest positive eigenvalue of the boundary value problem

Proof.
We just give a simple sketch here.
Case 1.
Under the Neumann boundary condition, that is,  . According to the eigenvalue theory of elliptic operators, the Laplacian
. According to the eigenvalue theory of elliptic operators, the Laplacian  on
on  with the Neumann boundary conditions is a self-adjoint operator with compact inverse, so there exists a sequence of nonnegative eigenvalues (going to
with the Neumann boundary conditions is a self-adjoint operator with compact inverse, so there exists a sequence of nonnegative eigenvalues (going to  ) and a sequence of corresponding eigenfunctions, which are denoted by
) and a sequence of corresponding eigenfunctions, which are denoted by  and
and  , respectively. In other words, we have
, respectively. In other words, we have

where  . Multiply the second equation of (2.10) by
. Multiply the second equation of (2.10) by  and integrate over
and integrate over  . By Green's theorem, we obtain
. By Green's theorem, we obtain

Clearly, (2.11) can also hold for  . The sequence of eigenfunctions
. The sequence of eigenfunctions  defines an orthonormal basis of
defines an orthonormal basis of  . For any
. For any  , we have
, we have

From (2.11) and (2.12), we can obtain

Case 2.
Under the Dirichlet boundary condition, that is,  . By the same may, we can obtained the inequality.
. By the same may, we can obtained the inequality.
This completes the proof.
Remark 2.5. (i) The lowest positive eigenvalue  in the boundary problem (2.9) is sometimes known as the first eigenvalue. (ii) The magnitude of
in the boundary problem (2.9) is sometimes known as the first eigenvalue. (ii) The magnitude of  is determined by domain
is determined by domain  . For example, let Laplacian on
. For example, let Laplacian on  , if
, if  and
and  , respectively, then
, respectively, then  and
and  [38, 39]. (iii) Although the eigenvalue
[38, 39]. (iii) Although the eigenvalue  of the laplacian with the Dirichlet boundary condition on a generally bounded domain
of the laplacian with the Dirichlet boundary condition on a generally bounded domain  cannot be determined exactly, a lower bound of it may nevertheless be estimated by
cannot be determined exactly, a lower bound of it may nevertheless be estimated by  , where
, where  is a surface area of the unit ball in
is a surface area of the unit ball in  ,
,  is a volume of domain
is a volume of domain  [40].
[40].
In Section 4, we will compare the results between this paper and previous literatures. To this end, we recall some previous results as follows (according to the symbols in this paper).
In [35], Wan and Zhou have studied the problem of convergence dynamics of model (2.1) with the Neumann boundary condition and obtained the following result (see [35, Theorem 3.1]).
3.1]).
Proposition 2.6.
Suppose that system (2.1) satisfies the assumptions (H1)–(H4) and
-
(A)
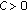 ,
, 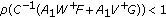 , where
, where  ,
,  ,
,  ,
,  ,
, 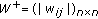 ,
,  ,
,  ,
,  . Also,
. Also,  denotes the spectral radius of a square matrix
denotes the spectral radius of a square matrix  .
.
Then model (2.1) is mean value exponentially stable.
Remark 2.7.
It should be noted that condition (A) in Proposition 2.6 is equivalent to  is a nonsingular
is a nonsingular  -matrix, where
-matrix, where  . Thus, the following result is treated as a special case of Proposition 2.6.
. Thus, the following result is treated as a special case of Proposition 2.6.
Proposition 2.8 (see [33, Theorem 3.1]).
Suppose that model (2.2) satisfies the assumptions (H2)–(H4) and
-
(B)
 is a nonsingular
is a nonsingular  -matrix, where
-matrix, where 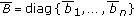 ,
, 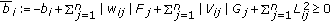 , for
, for  .
.
Then model (2.2) is almost surely exponentially stable.
Remark 2.9.
It is obvious that conditions (A) and (B) are irrelevant to the diffusion term. In other words, the diffusion term does not take effect in Propositions 2.6 and 2.8.
3. Main Results
Theorem 3.1.
Under assumptions (H1)–(H4), if the following conditions hold:
-
(H5)
 , for any
, for any  ,
,
where  is the lowest positive eigenvalue of problem (2.9),
is the lowest positive eigenvalue of problem (2.9),  ,
,  .
.
Then model (2.1) is almost surely exponentially stable.
Proof.
Let  be an any solution of model (2.1) and
be an any solution of model (2.1) and  . Model (2.1) is equivalent to
. Model (2.1) is equivalent to



where

for  .
.
It follows from (H5) that there exists a sufficiently small constant  such that
such that

To derive the almost surely exponential stability result, we construct the following Lyapunov functional:

By Itô's formula to  along (3.1a), we obtain
along (3.1a), we obtain

for  .
.
By the boundary condition, it is easy to calculate that

From assumptions (H1) and (H2), we have

From assumptions (H1) and (H3), we have

By the same way, we can obtain

Combining (3.6)–(3.9) into (3.5), we get

That is,

It is obvious that the right-hand side of (3.6) is a nonnegative semimartingale. From Lemma 2.3, it is easy to see that its limit is finite almost surely as  , which shows that
, which shows that

That is,

which implies

that is,

The proof is complete.
Theorem 3.2.
Under the conditions of Theorem 3.1, model (2.1) is mean square exponentially stable.
Proof.
Taking expectations on both sides of (3.11) and noticing that

we get

Since

we have

Also

By (3.17)–(3.20), we have

Let  .
.
Then, we easily get

The proof is completed.
By the similar way of the proof of Theorem 3.1, it is easy to prove the following results.
Theorem 3.3.
Under assumptions (H2)–(H4), if the following conditions hold:
-
(H6)
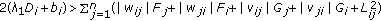 ,
, 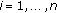 .
.
Then model (2.2) is almost surely exponentially stable and mean square exponentially stable.
Remark 3.4.
In the proof of Theorem 3.1, by Poincaré inequality, we have obtained  (see (3.6)). This is an important step that results in the condition of Theorem 3.1 including the diffusion terms.
(see (3.6)). This is an important step that results in the condition of Theorem 3.1 including the diffusion terms.
Remark 3.5.
It should be noted that assumptions (H5) and (H6) allow


respectively, which cannot guarantee the mean square exponential stability of the equilibrium solution of models (2.1) and (2.2). Thus, as we can see form Theorems 3.1, 3.2, and 3.3, reaction-diffusion terms do contribute the almost surely exponential stability and the mean square exponential stability of models (2.1) and (2.2), respectively. However, as we can see from Propositions 2.6 and 2.8, the diffusion term do not take effect in the convergence dynamics of delayed stochastic reaction-diffusion neural networks. Thus, the criteria what we proposed are less conservative and restrictive than Propositions 2.6 and 2.8.
Theorem 3.6.
Under assumptions (H1)–(H3), if
-
(H7)
 , for any
, for any  ,
,
holds, the equilibrium point of system (2.2) is globally exponentially stable.
Remark 3.7.
Theorem 3.6 shows that the globally exponential stability criteria on reaction-diffusion CGNNs with delays depend on the diffusion term. In exact words, diffusion terms have contributed to exponentially stabilization of reaction-diffusion CGNNs with delays. It should be noted that the authors in [24–28] have studied reaction-diffusion neural networks (including CGNNs and RNNs) with delays and obtained the sufficient condition of exponential stability. However, those sufficient condition are independent of the diffusion term. Obviously, the criteria what we proposed are less conservative and restrictive than those in [24–28].
4. Examples and Comparison
In order to illustrate the feasibility of our above established criteria in the preceding sections, we provide two concrete examples. Although the selection of the coefficients and functions in the examples is somewhat artificial, the possible application of our theoretical theory is clearly expressed.
Example 4.1.
Consider the following stochastic reaction-diffusion neural networks model on 

where  . It is clear that
. It is clear that  ,
,  ,
,  ,
,  . According to Remark 2.5, we can get
. According to Remark 2.5, we can get  . Taking
. Taking

we have

It follows from Theorem 3.3 that the equilibrium solution of such system is almost surely exponentially stable and mean square exponential stable.
Remark 4.2.
It should be noted that

it is well known, which cannot guarantee the mean square exponential stability of the equilibrium solution of model (4.1). Thus, as we can see in Example 4.1, the reaction-diffusion terms have contributed to the almost surely and mean square exponential stability of this model.
Example 4.3.
For the model (4.1), the diffusion operator, space  , and the Neumann boundary conditions are replaced by,
, and the Neumann boundary conditions are replaced by,

and the Dirichlet boundary condition

respectively. The remainder parameters and functions unchanged. According to Remark 2.5, we see that  . By the same way of Example 4.1, equilibrium solution of model (4.5) is almost surely exponentially stable and mean square.
. By the same way of Example 4.1, equilibrium solution of model (4.5) is almost surely exponentially stable and mean square.
Now, we compare the results in this paper with Propositions 2.6 and 2.8.
The authors in [33, 35] have considered the stochastic delayed reaction-diffusion neural networks with Neumann boundary condition and obtained the sufficient conditions to guarantee the almost surely or mean value exponential stability. We notice that the conditions of Propositions 2.6 and 2.8 do not include the diffusion terms, hence, in principal, Propositions 2.6 and 2.8 could be applied to analyze the exponential stability of stochastic system (4.1), but could not be model (4.5) for its the Dirichlet boundary condition. Unfortunately, Propositions 2.6 and 2.8 are not applicable to ascertain the exponential stability of model (4.1).
In fact, it is easy to calculate that

That is, condition (A) of Proposition 2.6 does not hold.
Next, we explain that Proposition 2.8 is not applicable to ascertain the almost surely exponential stability of system (4.1):

However,

is not a nonsingular  -matrix. This implies that condition (A) of Proposition 2.6 is not satisfied.
-matrix. This implies that condition (A) of Proposition 2.6 is not satisfied.
Remark 4.4.
The above comparison shows that reaction-diffusion term contributes to the exponentially stabilization of a stochastic reaction-diffusion neural network and the previous results have been improved.
5. Conclusion
The problem of the convergence dynamics for the stochastic reaction-diffusion CGNNs with delays has been studied in this paper. This neural networks is quite general, and can be used to describe some well-known neural networks, including Hopfield neural networks, cellular neural networks, and generalized CGNNs. By Poincaré inequality and constructing suitable Lyapunov functional, we obtain some sufficient condition to ensure the almost sure and mean square exponential stability of the system. It is worth noting that the diffusion term has played an important role in the obtained conditions, a significant feature that distinguishes the results in this paper from the previous. Two examples are given to show the effectiveness of the results. Moreover, the methods in this paper can been used to consider other stochastic delayed reaction-diffusion neural network model with the Neumann or Dirichlet boundary condition.
References
Arik S, Orman Z: Global stability analysis of Cohen-Grossberg neural networks with time varying delays. Physics Letters A 2005,341(5-6):410-421. 10.1016/j.physleta.2005.04.095
Chen Z, Ruan J: Global stability analysis of impulsive Cohen-Grossberg neural networks with delay. Physics Letters A 2005,345(1–3):101-111.
Chen Z, Ruan J: Global dynamic analysis of general Cohen-Grossberg neural networks with impulse. Chaos, Solitons & Fractals 2007,32(5):1830-1837. 10.1016/j.chaos.2005.12.018
Cohen MA, Grossberg S: Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Transactions on Systems, Man, and Cybernetics 1983,13(5):815-826.
Huang T, Chan A, Huang Y, Cao J: Stability of Cohen-Grossberg neural networks with time-varying delays. Neural Networks 2007,20(8):868-873. 10.1016/j.neunet.2007.07.005
Liao X, Li C, Wong K-W: Criteria for exponential stability of Cohen-Grossberg neural networks. Neural Networks 2004,17(10):1401-1414. 10.1016/j.neunet.2004.08.007
Liu X, Wang Q: Impulsive stabilization of high-order hopfield-type neural networks with time-varying delays. IEEE Transactions on Neural Networks 2008,19(1):71-79.
Yang Z, Xu D: Impulsive effects on stability of Cohen-Grossberg neural networks with variable delays. Applied Mathematics and Computation 2006,177(1):63-78. 10.1016/j.amc.2005.10.032
Zhang J, Suda Y, Komine H: Global exponential stability of Cohen-Grossberg neural networks with variable delays. Physics Letters A 2005,338(1):44-50. 10.1016/j.physleta.2005.02.005
Zhou Q: Global exponential stability for a class of impulsive integro-differential equation. International Journal of Bifurcation and Chaos 2008,18(3):735-743. 10.1142/S0218127408020616
Park JH, Kwon OM: Synchronization of neural networks of neutral type with stochastic perturbation. Modern Physics Letters B 2009,23(14):1743-1751. 10.1142/S0217984909019909
Park JH, Kwon OM: Delay-dependent stability criterion for bidirectional associative memory neural networks with interval time-varying delays. Modern Physics Letters B 2009,23(1):35-46. 10.1142/S0217984909017807
Park JH, Kwon OM, Lee SM: LMI optimization approach on stability for delayed neural networks of neutral-type. Applied Mathematics and Computation 2008,196(1):236-244. 10.1016/j.amc.2007.05.047
Meng Y, Guo S, Huang L: Convergence dynamics of Cohen-Grossberg neural networks with continuously distributed delays. Applied Mathematics and Computation 2008,202(1-2):188-199.
Arnold L: Stochastic Differential Equations: Theory and Applications. John Wiley & Sons, New York, NY, USA; 1972.
Blythe S, Mao X, Liao X: Stability of stochastic delay neural networks. Journal of the Franklin Institute 2001,338(4):481-495. 10.1016/S0016-0032(01)00016-3
Buhmann J, Schulten K: Influence of noise on the function of a "physiological" neural network. Biological Cybernetics 1987,56(5-6):313-327. 10.1007/BF00319512
Haykin S: Neural Networks. Prentice-Hall, Upper Saddle River, NJ, USA; 1994.
Sun Y, Cao J:
 th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007,8(4):1171-1185. 10.1016/j.nonrwa.2006.06.009
th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007,8(4):1171-1185. 10.1016/j.nonrwa.2006.06.009Wan L, Sun J: Mean square exponential stability of stochastic delayed Hopfield neural networks. Physics Letters A 2005,343(4):306-318. 10.1016/j.physleta.2005.06.024
Wan L, Zhou Q: Convergence analysis of stochastic hybrid bidirectional associative memory neural networks with delays. Physics Letters A 2007,370(5-6):423-432. 10.1016/j.physleta.2007.05.095
Zhao H, Ding N: Dynamic analysis of stochastic bidirectional associative memory neural networks with delays. Chaos, Solitons & Fractals 2007,32(5):1692-1702. 10.1016/j.chaos.2005.12.010
Zhou Q, Wan L: Exponential stability of stochastic delayed Hopfield neural networks. Applied Mathematics and Computation 2008,199(1):84-89. 10.1016/j.amc.2007.09.025
Zhao H, Ding N: Dynamic analysis of stochastic Cohen-Grossberg neural networks with time delays. Applied Mathematics and Computation 2006,183(1):464-470. 10.1016/j.amc.2006.05.087
Song Q, Cao J: Global exponential robust stability of Cohen-Grossberg neural network with time-varying delays and reaction-diffusion terms. Journal of the Franklin Institute 2006,343(7):705-719. 10.1016/j.jfranklin.2006.07.001
Song Q, Cao J: Exponential stability for impulsive BAM neural networks with time-varying delays and reaction-diffusion terms. Advances in Difference Equations 2007, 2007:-18.
Liang J, Cao J: Global exponential stability of reaction-diffusion recurrent neural networks with time-varying delays. Physics Letters A 2003,314(5-6):434-442. 10.1016/S0375-9601(03)00945-9
Wang L, Xu D: Global exponential stability of Hopfield reaction-diffusion neural networks with time-varying delays. Science in China. Series F 2003,46(6):466-474. 10.1360/02yf0146
Yang J, Zhong S, Luo W: Mean square stability analysis of impulsive stochastic differential equations with delays. Journal of Computational and Applied Mathematics 2008,216(2):474-483. 10.1016/j.cam.2007.05.022
Zhao H, Wang K: Dynamical behaviors of Cohen-Grossberg neural networks with delays and reaction-diffusion terms. Neurocomputing 2006,70(1–3):536-543.
Zhou Q, Wan L, Sun J: Exponential stability of reaction-diffusion generalized Cohen-Grossberg neural networks with time-varying delays. Chaos, Solitons & Fractals 2007,32(5):1713-1719. 10.1016/j.chaos.2005.12.003
Lv Y, Lv W, Sun J: Convergence dynamics of stochastic reaction-diffusion recurrent neural networks in continuously distributed delays. Nonlinear Analysis: Real World Applications 2008,9(4):1590-1606. 10.1016/j.nonrwa.2007.04.003
Sun J, Wan L: Convergence dynamics of stochastic reaction-diffusion recurrent neural networks with delays. International Journal of Bifurcation and Chaos 2005,15(7):2131-2144. 10.1142/S0218127405013332
Wan L, Zhou Q, Sun J: Mean value exponential stability of stochastic reaction-diffusion generalized Cohen-Grossberg neural networks with time-varying delay. International Journal of Bifurcation and Chaos 2007,17(9):3219-3227. 10.1142/S021812740701897X
Wan L, Zhou Q: Exponential stability of stochastic reaction-diffusion Cohen-Grossberg neural networks with delays. Applied Mathematics and Computation 2008,206(2):818-824. 10.1016/j.amc.2008.10.002
Wang L, Zhang Z, Wang Y: Stochastic exponential stability of the delayed reaction-diffusion recurrent neural networks with Markovian jumping parameters. Physics Letters A 2008,372(18):3201-3209. 10.1016/j.physleta.2007.07.090
Mao X: Stochastic Differential Equations and Applications. Horwood, Chichester, UK; 1997.
Temam R: Infinite-Dimensional Dynamical Systems in Mechanics and Physics, Applied Mathematical Sciences. Volume 68. Springer, New York, NY, USA; 1988:xvi+500.
Ye Q, Li Z: Introduction of Reaction-Diffusion Equation. Science Press, Beijing, China; 1999.
Niu P, Qu J, Han J: Estimation of the eigenvalue of Laplace operator and generalization. Journal of Baoji College of Arts and Science. Natural Science 2003,23(1):85-87.
Acknowledgments
The authors would like to thank the editor and the reviewers for their detailed comments and valuable suggestions which have led to a much improved paper. This paper is supported by National Basic Research Program of China (2010CB732501).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pan, J., Zhong, S. Dynamic Analysis of Stochastic Reaction-Diffusion Cohen-Grossberg Neural Networks with Delays. Adv Differ Equ 2009, 410823 (2009). https://doi.org/10.1155/2009/410823
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/410823
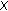 be an open bounded domain in
be an open bounded domain in 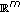 with smooth boundary
with smooth boundary 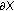 , and
, and  denotes the measure of
denotes the measure of  .
.  ;
;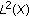 is the space of real Lebesgue measurable functions on
is the space of real Lebesgue measurable functions on 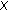 which is a Banach space for the
which is a Banach space for the 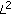 -norm
-norm 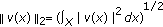 ,
, 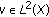 ;
; , where
, where 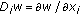 ,
, 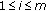 .
.  the closure of
the closure of  in
in 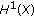 ;
; is the space of continuous functions which map
is the space of continuous functions which map  into
into  with the norm
with the norm  , for any
, for any  ;
; and be an
and be an 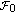 -measurable
-measurable 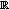 -valued random variable, where, for example,
-valued random variable, where, for example,  restricted on
restricted on 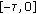 , and
, and  be the Banach space of continuous and bounded functions with the norm
be the Banach space of continuous and bounded functions with the norm  , where
, where 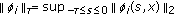 , for any
, for any  ,
,  ;
; is the gradient operator, for
is the gradient operator, for 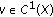 .
.  .
. 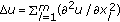 is the Laplace operator, for
is the Laplace operator, for  .
. is bounded, positive and continuous, that is, there exist constants
is bounded, positive and continuous, that is, there exist constants  ,
, 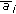 such that
such that 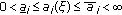 , for
, for 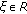 ,
, 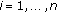 ,
, and
and  , for
, for 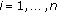 ,
,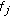 ,
, 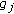 are bounded, and
are bounded, and  ,
, 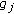 ,
, 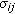 are Lipschitz continuous with Lipschitz constant
are Lipschitz continuous with Lipschitz constant  ,
, 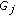 ,
, 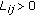 , for
, for 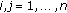 ,
,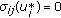 , for
, for  .
.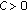 ,
, 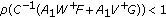 , where
, where  ,
,  ,
,  ,
,  ,
, 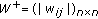 ,
,  ,
,  ,
,  . Also,
. Also,  denotes the spectral radius of a square matrix
denotes the spectral radius of a square matrix  .
. is a nonsingular
is a nonsingular  -matrix, where
-matrix, where 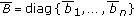 ,
, 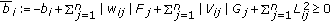 , for
, for  .
. , for any
, for any  ,
,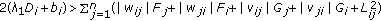 ,
, 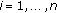 .
. , for any
, for any  ,
, th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007,8(4):1171-1185. 10.1016/j.nonrwa.2006.06.009
th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Analysis: Real World Applications 2007,8(4):1171-1185. 10.1016/j.nonrwa.2006.06.009