- Research Article
- Open access
- Published:
Multiple Positive Solutions for a Class of 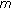 -Point Boundary Value Problems on Time Scales
-Point Boundary Value Problems on Time Scales
Advances in Difference Equations volume 2009, Article number: 219251 (2009)
Abstract
By constructing an available integral operator and combining Krasnosel'skii-Zabreiko fixed point theorem with properties of Green's function, this paper shows the existence of multiple positive solutions for a class of m-point second-order Sturm-Liouville-like boundary value problems on time scales with polynomial nonlinearity. The results significantly extend and improve many known results for both the continuous case and more general time scales. We illustrate our results by one example, which cannot be handled using the existing results.
1. Introduction
Recently, there have been many papers working on the existence of positive solutions to boundary value problems for differential equations on time scales; see, for example, [1–20]. This has been mainly due to its unification of the theory of differential and difference equations. An introduction to this unification is given in [11, 12, 18, 19]. Now, this study is still a new area of fairly theoretical exploration in mathematics. However, it has led to several important applications, for example, in the study of insect population models, neural networks, heat transfer, and epidemic models; see, for example, [10, 11]. For some other excellent results and applications of the case that boundary value problems on time scales to a variety of problems from Khan et al. [21], Agarose et al. [22], Wang [23], Sun [24], Feng et al. [25], Feng et al. [26] and Feng et al. [27].
Motivated by the works mentioned above, we intend in this paper to study the existence of multiple positive solutions for the second-order m-point nonlinear dynamic equation on time scales with polynomial nonlinearity:

where  is a time scale,
is a time scale,

the points  for
for  with
with  ;
;


Recently, Xu [28] considered the following second-order two-point impulsive singular differential equations boundary value problem:

By means of fixed point index theory in a cone, the author established the existence of two nonnegative solutions for problem (1.5).
More recently, by applying Guo-Krasnosel'skii fixed point theorem in a cone, Anderson and Ma [6] established the existence of at least one positive solution to the multipoint time-scale eigenvalue problem:

where  is continuous.
is continuous.
As far as we know, there is no paper to study the existence of multiple positive solutions to problem (1.1) on time scales with polynomial nonlinearity. The objective of the present paper is to fill this gap. On the other hand, many difficulties occur when we study BVPs on time scales. For example, basic tools from calculus such as Fermat's theorem, Rolle's theorem and the intermediate value theorem may not necessarily hold. So it is interesting and important to discuss the problem (1.1). The purpose of this paper is to prove that the problem (1.1) possesses at least two positive solutions. Moreover, the methods used in this paper are different from [6, 28] and the results obtained in this paper generalize some results in [6, 28] to some degree.
The time scale related notations adopted in this paper can be found, if not explained specifically, in almost all literature related to time scales. The readers who are unfamiliar with this area can consult for example [11, 12, 18, 19] for details.
For convenience, we list the following well-known definitions.
Definition 1.1.
A time scale  is a nonempty closed subset of
is a nonempty closed subset of  .
.
Definition 1.2.
Define the forward (backward) jump operator  at
at  for
for  at
at  for
for  by
by  for all
for all  .
.
We assume throughout that  has the topology that it inherits from the standard topology on
has the topology that it inherits from the standard topology on  and say
and say  is right-scattered, left-scattered, right-dense and left-dense if
is right-scattered, left-scattered, right-dense and left-dense if  and
and  , respectively. Finally, we introduce the sets
, respectively. Finally, we introduce the sets  and
and  . which are derived from the time scale
. which are derived from the time scale  as follows. If
as follows. If  has a left-scattered maximum
has a left-scattered maximum  , then
, then  , otherwise
, otherwise  . If
. If  has a right-scattered minimum
has a right-scattered minimum  , then
, then  ,
,  .
.
Definition 1.3.
Fix  and let
and let  . Define
. Define  to be the number (if it exists) with the property that given
to be the number (if it exists) with the property that given  there is a neighborhood
there is a neighborhood  of
of  with
with

for all  , where
, where  denotes the (delta) derivative of
denotes the (delta) derivative of  with respect to the first variable, then
with respect to the first variable, then

implies

Definition 1.4.
 . Define
. Define  to be the number (if it exists) with the property that given
to be the number (if it exists) with the property that given  there is a neighborhood
there is a neighborhood  of
of  with
with

for all  . Call
. Call  the nabla derivative of
the nabla derivative of  at the point
at the point  .
.
If  then
then  . If
. If  then
then  is the forward difference operator while
is the forward difference operator while  is the backward difference operator.
is the backward difference operator.
Definition 1.5.
A function  is called rd-continuous provided it is continuous at all right dense points of
is called rd-continuous provided it is continuous at all right dense points of  and its left sided limit exists (finite) at left dense
and its left sided limit exists (finite) at left dense  . We let
. We let  denote the set of rd-continuous functions
denote the set of rd-continuous functions  .
.
Definition 1.6.
 is called ld-continuous provided it is continuous at all left
is called ld-continuous provided it is continuous at all left  and its right sided limit exists (finite) at right dense
and its right sided limit exists (finite) at right dense  . We let
. We let  denote the set of ld-continuous
denote the set of ld-continuous  .
.
Definition 1.7.
A function  is called a delta-antiderivative of
is called a delta-antiderivative of  provided
provided  holds for all
holds for all  . In this case we define the delta integral of
. In this case we define the delta integral of  by
by

for all  .
.
Definition 1.8.
 is called a nabla-antiderivative of
is called a nabla-antiderivative of  provided
provided  holds for all
holds for all  . In this case we define the nabla integral of f by
. In this case we define the nabla integral of f by

for all  .
.
2. Preliminaries
In this section, we provide some necessary background. In particular, we state some properties of Green's function associated with problem (1.1), and we then state a fixed-point theorem which is crucial to prove our main results.
The basic space used in this paper is  . It is well known that
. It is well known that  is a Banach space with the norm
is a Banach space with the norm  defined by
defined by  . Let
. Let  be a cone of
be a cone of  ,
,  , where
, where  .
.
In this paper, the Green's function of the corresponding homogeneous BVP is defined by

where

and  and
and  satisfy
satisfy

respectively.
Lemma 2.1 (see [6]).
Assume that (1.2) and (1.3) hold. Then  and the functions
and the functions  and
and  satisfy
satisfy

From Lemma 2.1 and the definition of  , we can prove that
, we can prove that  has the following properties.
has the following properties.
Proposition 2.2.
For  , one has
, one has

where 
In fact, from Lemma 2.1, we have  for
for  Therefore (2.5) holds.
Therefore (2.5) holds.
Proposition 2.3.
If (1.2) holds, then for  , one has
, one has

Proof.
In fact, from Lemma 2.1, we obtain  for
for  So
So  .
.
On the other hand, from Lemma 2.1, we know that  for
for  . This together with
. This together with  implies that
implies that  for
for  . Hence
. Hence  is nondecreasing on
is nondecreasing on  ,
,  is nonincreasing on
is nonincreasing on  . So (2.6) holds.
. So (2.6) holds.
Proposition 2.4.
For all  one has
one has

where

Proof.
In fact, for  , we have
, we have

Therefore (2.7) holds.
It is easy to see that  , for
, for  . Thus, there exists
. Thus, there exists  such that
such that  for
for  , where
, where

We remark that Proposition 2.2 implies that there exists  such that for
such that for 

Set

Lemma 2.5 (see [6]).
Assume that (1.2) and (1.3) hold. If  and
and  , then the nonhomogeneous boundary value problem
, then the nonhomogeneous boundary value problem

has a unique solution  for which the formula
for which the formula

holds, where


By similar method, one can define

The following lemma is crucial to prove our main results.
Let  and
and  be two bounded open sets in a real Banach space
be two bounded open sets in a real Banach space  , such that
, such that  and
and  . Let the operator
. Let the operator  be completely continuous, where
be completely continuous, where  is a cone in
is a cone in  . Suppose that one of the two conditions
. Suppose that one of the two conditions

or

is satisfied. Then  has at least one fixed point in
has at least one fixed point in  .
.
3. Main Results
In this section, we apply Lemma 2.6 to establish the existence of at least two positive solutions for BVP (1.1).
The following assumptions will stand throughout this paper.
(H1)There exist  such that
such that

where  and
and  are defined in (1.4), respectively.
are defined in (1.4), respectively.
(H2)We have

for  and
and  given in (2.2) and (2.12), respectively.
given in (2.2) and (2.12), respectively.
If  holds, then we can show that
holds, then we can show that  have the following properties.
have the following properties.
Proposition 3.1.
If (1.2)–(1.4) and  hold, then from (2.15), for
hold, then from (2.15), for  , one has
, one has

where 
Proof.
Let

Then from (1.2)–(1.4) and  , we obtain
, we obtain  Therefore,
Therefore, 
On the other hand, since

we have  So one has
So one has

This and  imply (3.3) holds.
imply (3.3) holds.
Proposition 3.2.
If (1.2)–(1.4) and  hold, then from (2.16),
hold, then from (2.16),  , one has
, one has

Proof.
The proof is similar to that of Proposition 3.1. So we omit it.
For the sake of applying fixed point theorem on cone, we construct a cone in  by
by

where  is defined in (2.10).
is defined in (2.10).
Define  by
by

By (2.14), it is well known that the problem (1.1) has a positive solution  if and only if
if and only if  is a fixed point of
is a fixed point of  .
.
Lemma 3.3.
Suppose that (1.2)–(1.4) and  -
- hold. Then
hold. Then  and
and  is completely continuous.
is completely continuous.
Proof.
For  by (2.14), we have
by (2.14), we have  and
and

On the other hand, for  , by (3.9),(3.10) and (2.7), we obtain
, by (3.9),(3.10) and (2.7), we obtain

Therefore  , that is,
, that is,  .
.
Next by standard methods and the Ascoli-Arzela theorem one can prove that  is completely continuous. So it is omitted.
is completely continuous. So it is omitted.
Theorem 3.4.
Suppose that (1.2)–(1.4) and  -
- hold. Then problem (1.1) has at least two positive solutions provided
hold. Then problem (1.1) has at least two positive solutions provided

where  and
and  are defined in (3.3), (3.7) and in Proposition 3.1, respectively.
are defined in (3.3), (3.7) and in Proposition 3.1, respectively.
Proof.
Let  be the cone preserving, completely continuous operator that was defined by (3.9).
be the cone preserving, completely continuous operator that was defined by (3.9).
Let  , where
, where  . Choosing
. Choosing  and
and  satisfy
satisfy

Now we prove that


In fact, if there exists  such that
such that  , then for
, then for  , we have
, we have

where  defined by (2.17).
defined by (2.17).
Therefore  , that is,
, that is,  , which is a contradiction. Hence (3.14) holds.
, which is a contradiction. Hence (3.14) holds.
Next, turning to (3.15). If there exists  such that
such that  , then for
, then for  , we have
, we have

where  are defined by (2.17).
are defined by (2.17).
Therefore  , that is,
, that is,  , which is a contradiction. Hence (3.15) holds.
, which is a contradiction. Hence (3.15) holds.
It remains to prove

In fact, if there exists  such that
such that  , then for
, then for  , we have
, we have

that is,

which is a contradiction, where  are defined by (2.17). Hence (3.18) holds. From Lemma 2.6, (3.14), (3.15) and (3.18) yield that the problem (1.1) has at least two solutions
are defined by (2.17). Hence (3.18) holds. From Lemma 2.6, (3.14), (3.15) and (3.18) yield that the problem (1.1) has at least two solutions  and
and  . The proof is complete.
. The proof is complete.
4. Example
Example 4.1.
To illustrate how our main results can be used in practice we present an example.
Let  . Take
. Take  in (1.1). Now we consider the following three point boundary value problem
in (1.1). Now we consider the following three point boundary value problem

where

It is not difficult to see that

On the other hand, by calculating we have  ,
,

and 

Let  . Then
. Then  and
and

It follows that  and
and  hold.
hold.
Finally, we prove that

In fact, from  , we have
, we have  and
and

Therefore, the conditions of Theorem 3.4 hold. Hence problem (4.1) has at least two positive solutions.
Remark 4.2.
Example 4.1 implies that there is a large number of functions that satisfy the conditions of Theorem 3.4. In addition, the conditions of Theorem 3.4 are also easy to check.
References
Agarwal RP, Bohner M, Wong PJY: Sturm-Liouville eigenvalue problems on time scales. Applied Mathematics and Computation 1999,99(2–3):153–166. 10.1016/S0096-3003(98)00004-6
Avery RI, Anderson DR: Existence of three positive solutions to a second-order boundary value problem on a measure chain. Journal of Computational and Applied Mathematics 2002,141(1–2):65–73. 10.1016/S0377-0427(01)00436-8
Henderson J: Multiple solutions for th order Sturm-Liouville boundary value problems on a measure chain. Journal of Difference Equations and Applications 2000,6(4):417–429. 10.1080/10236190008808238
Anderson D, Avery R, Henderson J: Existence of solutions for a one dimensional -Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889–896. 10.1080/10236190410001731416
Bohner M, Luo H: Singular second-order multipoint dynamic boundary value problems with mixed derivatives. Advances in Difference Equations 2006, 2006:-15.
Anderson DR, Ma R: Second-order -point eigenvalue problems on time scales. Advances in Difference Equations 2006, 2006:-17.
Peterson AC, Raffoul YN, Tisdell CC: Three point boundary value problems on time scales. Journal of Difference Equations and Applications 2004,10(9):843–849. 10.1080/10236190410001702481
Henderson J, Tisdell CC: Topological transversality and boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004,289(1):110–125. 10.1016/j.jmaa.2003.08.030
Henderson J, Peterson A, Tisdell CC: On the existence and uniqueness of solutions to boundary value problems on time scales. Advances in Difference Equations 2004,2004(2):93–109. 10.1155/S1687183904308071
Agarwal RP, Bohner M, Li W-T: Nonoscillation and Oscillation: Theory for Functional Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 267. Marcel Dekker, New York, NY, USA; 2004:viii+376.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Anderson DR: Extension of a second-order multi-point problem to time scales. Dynamic Systems and Applications 2003,12(3–4):393–403.
Erbe L, Peterson A: Green's functions and comparison theorems for differential equations on measure chains. Dynamics of Continuous, Discrete and Impulsive Systems 1999,6(1):121–137.
Anderson DR: Eigenvalue intervals for a two-point boundary value problem on a measure chain. Journal of Computational and Applied Mathematics 2002,141(1–2):57–64. 10.1016/S0377-0427(01)00435-6
He Z, Jiang X: Triple positive solutions of boundary value problems for -Laplacian dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2006,321(2):911–920. 10.1016/j.jmaa.2005.08.090
Chyan CJ, Henderson J: Eigenvalue problems for nonlinear differential equations on a measure chain. Journal of Mathematical Analysis and Applications 2000,245(2):547–559. 10.1006/jmaa.2000.6781
Lakshmikantham V, Sivasundaram S, Kaymakcalan B: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1–2):18–56.
Erbe L, Peterson A, Saker SH: Hille-Kneser-type criteria for second-order dynamic equations on time scales. Advances in Difference Equations 2006, 2006:-18.
Khan RA, Nieto JJ, Otero-Espinar V: Existence and approximation of solution of three-point boundary value problems on time scales. Journal of Difference Equations and Applications 2008,14(7):723–736. 10.1080/10236190701840906
Agarose RP, Other-Espial V, Parera K, Vivre DR: Multiple positive solutions in the sense of distributions of singular BAPS on time scales and an application to Eden-Fowler equations. Advances in Difference Equations 2008, 2008:-13.
Wang D-B: Three positive solutions of three-point boundary value problems for -Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2172–2180. 10.1016/j.na.2007.01.037
Sun J-P: A new existence theorem for right focal boundary value problems on a measure chain. Applied Mathematics Letters 2005,18(1):41–47. 10.1016/j.aml.2003.04.008
Feng M, Zhang X, Ge W: Positive solutions for a class of boundary value problems on time scales. Computers & Mathematics with Applications 2007,54(4):467–475. 10.1016/j.camwa.2007.01.031
Feng M-Q, Li X-G, Ge W-G: Triple positive solutions of fourth-order four-point boundary value problems of -Laplacian dynamic equations on time scales. Advances in Difference Equations 2008, 2008:-9.
Feng M, Feng H, Zhang X, Ge W: Triple positive solutions for a class of -point dynamic equations on time scales with -Laplacian. Mathematical and Computer Modelling 2008,48(7–8):1213–1226. 10.1016/j.mcm.2007.12.016
Xu X: Multiple solutions for impulsive singular differential equations boundary value problems, Doctorial thesis. Shandong University, Shandong, China; 2001.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgments
This work is sponsored by the National Natural Science Foundation of China (10671012) and the Scientific Creative Platform Foundation of Beijing Municipal Commission of Education (PXM2008-014224-067420). The authors thank the referee for his careful reading of the manuscript and useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feng, M., Zhang, X. & Ge, W. Multiple Positive Solutions for a Class of 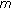 -Point Boundary Value Problems on Time Scales.
Adv Differ Equ 2009, 219251 (2009). https://doi.org/10.1155/2009/219251
-Point Boundary Value Problems on Time Scales.
Adv Differ Equ 2009, 219251 (2009). https://doi.org/10.1155/2009/219251
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/219251