- Research Article
- Open access
- Published:
Dynamical Properties for a Class of Fourth-Order Nonlinear Difference Equations
Advances in Difference Equations volume 2008, Article number: 678402 (2007)
Abstract
We consider the dynamical properties for a kind of fourth-order rational difference equations. The key is for us to find that the successive lengths of positive and negative semicycles for nontrivial solutions of this equation periodically occur with same prime period 5. Although the period is same, the order for the successive lengths of positive and negative semicycles is completely different. The rule is  or
or  or
or  . By the use of the rule, the positive equilibrium point of this equation is proved to be globally asymptotically stable.
. By the use of the rule, the positive equilibrium point of this equation is proved to be globally asymptotically stable.
1. Introduction and Preliminaries
Rational difference equation, as a kind of typical nonlinear difference equations, is always a subject studied in recent years. Especially, some prototypes for the development of the basic theory of the global behavior of nonlinear difference equations of order greater than one come from the results of rational difference equations. For the systematical investigations of this aspect, refer to the monographs [1–3], the papers [4–9], and the references cited therein.
Motivated by the work [5–7], we consider in this paper the following fourth-order rational difference equation:

where

the parameter  ,
,  ,
,  , and the initial values
, and the initial values  .
.
Mainly, by analyzing the rule for the length of semicycle to occur successively, we clearly describe out the rule for the trajectory structure of its solutions. With the help of several key lemmas, we further derive the global asymptotic stability of positive equilibrium of (1.1). To the best of our knowledge, (1.1) has not been investigated so far; therefore, it is theoretically meaningful to study its qualitative properties.
It is easy to see that the positive equilibrium  of (1.1) satisfies
of (1.1) satisfies

From this, we see that (1.1) possesses a unique positive equilibrium 
It is essential in this note for us to obtain the general rule for the trajectory structure of solutions of (1.1) as follows.
Theorem 1.1.
The rule for the trajectory structure of any solution of (1.1) is as follows:
-
(i)
the solution is either eventually trivial,
-
(ii)
or the solution is eventually nontrivial,
-
(1)
and further, either the solution is eventually positive nonoscillatory,
-
(2)
or the solution is strictly oscillatory, and moreover, the successive lengths for positive and negative semicycles occur periodically with prime period 5, and the rule is
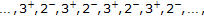 or
or 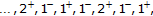
 or
or 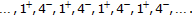
-
(1)
The positive equilibrium point of (1.1) is a global attractor of all its solutions.
It follows from the results stated in the sequel that Theorem 1.1 is true.
For the corresponding concepts in this paper, see [3] or the papers [5–7].
2. Nontrivial Solution
Theorem 2.1.
A positive solution  of (1.1) is eventually trivial if and only if
of (1.1) is eventually trivial if and only if

Proof.
Sufficiency. Assume that (2.1) holds. Then, according to (1.1), we know that the following conclusions are true: if  or
or  then
then  for
for 
Necessity. Conversely, assume that

Then, we can show that  for any
for any  For the sake of contradiction, assume that for some
For the sake of contradiction, assume that for some 

Clearly,

From this, we can know that

which implies that  or
or  This contradicts (2.3).
This contradicts (2.3).
Remark 2.2.
Theorem 2.1 actually demonstrates that a positive solution  of (1.1) is eventually nontrivial if
of (1.1) is eventually nontrivial if  . So, if a solution is a nontrivial one, then
. So, if a solution is a nontrivial one, then  for any
for any  .
.
3. Several Key Lemmas
We state several key lemmas in this section, which will be important in the proofs of the sequel. Denote  for any integer
for any integer  .
.
Lemma 3.1.
If the integer  , then
, then

where

Lemma 3.2.
If the integer  ,
,  then
then

where

Lemma 3.3.
If the integer  ,
,  then
then

where

The results of Lemmas 3.1, 3.2, and 3.3 can be easily obtained from (1.1), and so we omit their proofs here.
Lemma 3.4.
Let  be a positive solution of (1.1) which is not eventually equal to 1, then the following conclusions are valid:
be a positive solution of (1.1) which is not eventually equal to 1, then the following conclusions are valid:
-
(a)
 for
for 
-
(b)
 for
for 
-
(c)
 for
for 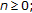
-
(d)
 for
for 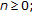
-
(e)
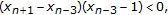 for
for 
Proof.
First, let us investigate (a). According to (1.1), it follows that

So,

Noting that  ,
,  , one has
, one has  , and
, and  From those, one can easily obtain the result of (a).
From those, one can easily obtain the result of (a).
Second, (b) comes. From (3.1), we obtain

where

From  and
and  , being eventually not equal to 1, one can see that
, being eventually not equal to 1, one can see that

This tells us that  That is,
That is,  So, the proof of (b) is complete.
So, the proof of (b) is complete.
Third, let us prove (c). From (3.1) one has

where

From (3.3), one gets

where

According to  and
and  , being eventually not equal to 1, one arrives at
, being eventually not equal to 1, one arrives at

From (3.14), (3.15), and (3.16), we know that  So, we can get immediately
So, we can get immediately

From (3.5), one can have

where

From (3.16), (3.18), and (3.19), we can obtain  that is,
that is,

By virtue of (3.12), (3.13), (3.17), and (3.20), we see that (c) is true.
The proofs of (d) and (e) are similar to those of (c). The proof for this lemma is complete.
Lemma 3.5.
Let  be a positive solution of (1.1) which is not eventually equal to 1, then
be a positive solution of (1.1) which is not eventually equal to 1, then  for
for 
Proof.
From (3.1), one has

where

From (3.3), one has

where

Noticing that  , we have
, we have

From (3.23), (3.24), and (3.25), we know that  So,
So,

From (3.5), one can recognize that

where

From (3.25), (3.27), and (3.28), we derive  So,
So,

Equation (3.5) shows that

where

By using (3.26), (3.29), (3.30), and (3.31), and noting that  when
when  we get
we get  Hence,
Hence,

It follows from (3.3) that

where

By virtue of (3.26), (3.29), (3.33), and (3.34), as well as  for
for  one has
one has  Accordingly,
Accordingly,

Equation (3.3) instructs us that

where

By virtue of (3.32), (3.35), (3.36), and (3.37), together with  when
when  one sees that
one sees that  So,
So,

From (3.5), one obtains

where

By virtue of (3.32), (3.35), (3.39), and (3.40), in addition to  when
when  one can see that
one can see that  Thus,
Thus,

From (3.3), we can see that

where

Utilizing (3.38), (3.41), (3.42), and (3.43), and adding  when
when  we know that the following is true:
we know that the following is true:  So,
So,

Similar to (3.44), by virtue of (3.5), (3.38), (3.41), and  when
when  we know that
we know that  is true. So,
is true. So,

From (3.21), (3.22), (3.44), and (3.45), one knows that the following is true:

This shows that Lemma 3.5 is true.
4. Oscillation and Nonoscillation
Theorem 4.1.
There exist nonoscillatory solutions of (1.1) with  ,
,  ,
,  , which must be eventually positive. There are not eventually negative nonoscillatory solutions of (1.1).
, which must be eventually positive. There are not eventually negative nonoscillatory solutions of (1.1).
Proof.
Consider a solution of (1.1) with  We then know from Lemma 3.4(a) that
We then know from Lemma 3.4(a) that  for
for  . So, this solution is just a nonoscillatory solution and it is, furthermore, eventually positive.
. So, this solution is just a nonoscillatory solution and it is, furthermore, eventually positive.
Suppose that there exist eventually negative nonoscillatory solutions of (1.1). Then, there exists a positive integer  such that
such that  for
for  . Thereout, for
. Thereout, for  ,
,  This contradicts Lemma 3.4(a). So, there are not eventually negative nonoscillatory solutions of (1.1), as desired.
This contradicts Lemma 3.4(a). So, there are not eventually negative nonoscillatory solutions of (1.1), as desired.
5. Rule of Cycle Length
Theorem 5.1.
Let  be a strictly oscillatory solution of (1.1), then the rule for the lengths of positive and negative semicycles of this solution to occur successively is
be a strictly oscillatory solution of (1.1), then the rule for the lengths of positive and negative semicycles of this solution to occur successively is 
 or
or  or
or 

Proof.
By Lemma 3.4(a), one can see that the length of a negative semicycle is at most 4, and that of a positive semicycle is at most 3. On the basis of the strictly oscillatory character of the solution, we see, for some integer  , that one of the following sixteen cases must occur:
, that one of the following sixteen cases must occur:
-
(1)
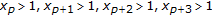 ;
; -
(2)
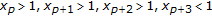 ;
; -
(3)
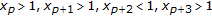 ;
; -
(4)
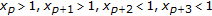 ;
; -
(5)
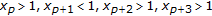 ;
; -
(6)
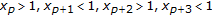 ;
; -
(7)
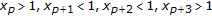 ;
; -
(8)
 ;
; -
(9)
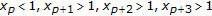 ;
; -
(10)
 ;
; -
(11)
 ;
; -
(12)
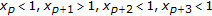 ;
; -
(13)
 ;
; -
(14)
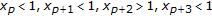 ;
; -
(15)
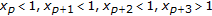 ;
; -
(16)
 .
.
If case (1) occurs, of course, it will be a nonoscillatory solution of (1.1).
If case (2) occurs, it follows from Lemma 3.4(a) that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
This means that the rule for the lengths of positive and negative semicycles of the solution of (1.1) to occur successively is

If case (3) occurs, it follows from Lemma 3.4(a) that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  which means that the rule for the lengths of positive and negative semicycles of the solution of (1.1) to occur successively is
which means that the rule for the lengths of positive and negative semicycles of the solution of (1.1) to occur successively is

If case 8 is reached, Lemma 3.4(a) tells us that  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
This implies that the rule for the lengths of positive and negative semicycles of the solution of (1.1) to occur successively is

Moreover, the rule for the cases (2.3), (3.5), (3.13), (3.15), and (3.17) is the same as that of case (2.1). And cases (3.1), (3.3), and (3.15) are completely similar to case (3) except possibly for the first semicycle. And cases (3.16), (3.18), (3.19), and (3.20) are like case (8) with a possible exception for the first semicycle.
Up to now, the proof of Theorem 5.1 is complete.
6. Global Asymptotic Stability
First, we consider the local asymptotic stability for unique positive equilibrium point  of (1.1). We have the following result.
of (1.1). We have the following result.
Theorem 6.1.
The positive equilibrium point of (1.1) is locally asymptotically stable.
Proof.
The linearized equation of (1.1) about the positive equilibrium point  is
is

and so it is clear from [3, Remark 1.3.7] that the positive equilibrium point  of (1.1) is locally asymptotically stable. The proof is complete.
of (1.1) is locally asymptotically stable. The proof is complete.
We are now in a position to study the global asymptotic stability of positive equilibrium point  .
.
Theorem 6.2.
The positive equilibrium point of (1.1) is globally asymptotically stable.
Proof.
We must prove that the positive equilibrium point  of (1.1) is both locally asymptotically stable and globally attractive. Theorem 6.1 has shown the local asymptotic stability of
of (1.1) is both locally asymptotically stable and globally attractive. Theorem 6.1 has shown the local asymptotic stability of  . Hence, it remains to verify that every positive solution
. Hence, it remains to verify that every positive solution  of (1.1) converges to
of (1.1) converges to  as
as  Namely, we want to prove that
Namely, we want to prove that

We can divide the solutions into two types:
-
(i)
trivial solutions;
-
(ii)
nontrivial solutions.
If a solution is a trivial one, then it is obvious for (6.2) to hold because  holds eventually.
holds eventually.
If the solution is a nontrivial one, then we can further divide the solution into two cases:
-
(a)
nonoscillatory solution;
-
(b)
oscillatory solution.
Consider now  to be nonoscillatory about the positive equilibrium point
to be nonoscillatory about the positive equilibrium point  of (1.1). By virtue of Lemma 3.4(b), it follows that the solution is monotonic and bounded. So,
of (1.1). By virtue of Lemma 3.4(b), it follows that the solution is monotonic and bounded. So,  exists and is finite. Taking limits on both sides of (1.1), one can easily see that (6.2) holds.
exists and is finite. Taking limits on both sides of (1.1), one can easily see that (6.2) holds.
Now, let  be strictly oscillatory about the positive equilibrium point of (1.1). By virtue of Theorem 5.1, one understands that the rule for the lengths of positive and negative semicycles occurring successively is
be strictly oscillatory about the positive equilibrium point of (1.1). By virtue of Theorem 5.1, one understands that the rule for the lengths of positive and negative semicycles occurring successively is
-
(i)
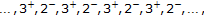
-
(ii)
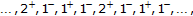 or
or -
(iii)

Now, we consider the case (i). For simplicity, for some nonnegative integer  we denote by
we denote by  the terms of a positive semicycle of the length three, and by
the terms of a positive semicycle of the length three, and by  a negative semicycle with semicycle length of two, then a positive semicycle and a negative semicycle, and so on. Namely, the rule for the lengths of positive and negative semicycles to occur successively can be periodically expressed as follows:
a negative semicycle with semicycle length of two, then a positive semicycle and a negative semicycle, and so on. Namely, the rule for the lengths of positive and negative semicycles to occur successively can be periodically expressed as follows:

Lemma 3.4(b), (c), (d), (e) and Lemma 3.5 teach us that the following results are true:
-
(a)

-
(b)

So, by virtue of (a), one can see that  is decreasing with lower bound 1. So, its limit exists and is finite, denoted by
is decreasing with lower bound 1. So, its limit exists and is finite, denoted by  . Moreover, the limits of
. Moreover, the limits of  and
and  are all equal to that of
are all equal to that of  .
.
Similarly, using (b), one can see that  is increasing with upper bound 1. So, its limit exists and is finite too. Furthermore, the limits of
is increasing with upper bound 1. So, its limit exists and is finite too. Furthermore, the limits of  are equal to that of
are equal to that of  , and one can assume the limits of it to be
, and one can assume the limits of it to be  . It is easy to see that
. It is easy to see that  It suffices to show that
It suffices to show that 
Noting that


and taking limits on both sides of (6.4) and (6.5), respectively, we get

From (6.6), we can show that  . Otherwise, assume that
. Otherwise, assume that

From (3.1), with both  and
and  being replaced by
being replaced by  , we get
, we get

Taking limits on both sides of the above equation, we can obtain

By virtue of (6.7), one has 
 , and
, and  when
when  and so, one will get
and so, one will get

This contradicts (6.9). Thus,  . Similarly, we can get
. Similarly, we can get  . Therefore, (6.2) holds when case (i) occurs.
. Therefore, (6.2) holds when case (i) occurs.
When case (ii) or (iii) occurs, using the method similar to that proving case (i), we can prove that (6.2) is also true. Thus, the proof of Theorem is complete.
References
Kulenović MRS, Ladas G: Dynamics of Second Order Rational Difference Equations, with Open Problems and Conjectures. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xii+218.
Agarwal RP: Difference Equations and Inequalities. Theory, Methods, and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 155. Marcel Dekker, New York, NY, USA; 1992:xiv+777.
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+228.
Amleh AM, Grove EA, Ladas G, Georgiou DA:On the recursive sequence
 . Journal of Mathematical Analysis and Applications 1999, 233(2):790-798. 10.1006/jmaa.1999.6346
. Journal of Mathematical Analysis and Applications 1999, 233(2):790-798. 10.1006/jmaa.1999.6346Xianyi L, Deming Z: Global asymptotic stability in a rational equation. Journal of Difference Equations and Applications 2003, 9(9):833-839. 10.1080/1023619031000071303
Li X, Zhu D: Global asymptotic stability of a nonlinear recursive sequence. Applied Mathematics Letters 2004, 17(7):833-838. 10.1016/j.aml.2004.06.014
Li X: Qualitative properties for a fourth-order rational difference equation. Journal of Mathematical Analysis and Applications 2005, 311(1):103-111. 10.1016/j.jmaa.2005.02.063
Xi H, Sun T: Global behavior of a higher-order rational difference equation. Advances in Difference Equations 2006, 2006:-7.
Rhouma MB, El-Sayed MA, Khalifa AK:On a
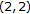 -rational recursive sequence. Advances in Difference Equations 2005, 2005(3):319-332. 10.1155/ADE.2005.319
-rational recursive sequence. Advances in Difference Equations 2005, 2005(3):319-332. 10.1155/ADE.2005.319
Acknowledgments
This work was partly supported by NNSF of China (Grant no. 10771094), and the Foundations for "New Century Engineering of 121 Talents in Hunan Province" and "Chief Professor of Mathematical Discipline in Hunan Province."
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, D., Li, P. & Li, X. Dynamical Properties for a Class of Fourth-Order Nonlinear Difference Equations. Adv Differ Equ 2008, 678402 (2007). https://doi.org/10.1155/2008/678402
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/678402
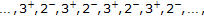 or
or 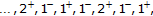
 or
or 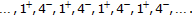
 for
for 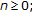
 for
for 
 for
for 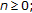
 for
for 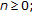
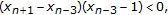 for
for 
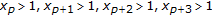 ;
;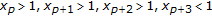 ;
;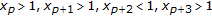 ;
;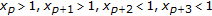 ;
;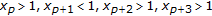 ;
;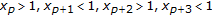 ;
;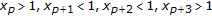 ;
; ;
;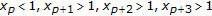 ;
; ;
; ;
;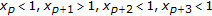 ;
; ;
;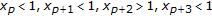 ;
;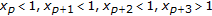 ;
; .
.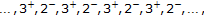
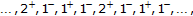 or
or


 . Journal of Mathematical Analysis and Applications 1999, 233(2):790-798. 10.1006/jmaa.1999.6346
. Journal of Mathematical Analysis and Applications 1999, 233(2):790-798. 10.1006/jmaa.1999.6346 -rational recursive sequence. Advances in Difference Equations 2005, 2005(3):319-332. 10.1155/ADE.2005.319
-rational recursive sequence. Advances in Difference Equations 2005, 2005(3):319-332. 10.1155/ADE.2005.319