- Research Article
- Open access
- Published:
A Note on Symmetric Properties of the Twisted  -Bernoulli Polynomials and the Twisted Generalized
-Bernoulli Polynomials and the Twisted Generalized  -Bernoulli Polynomials
-Bernoulli Polynomials
Advances in Difference Equations volume 2010, Article number: 801580 (2010)
Abstract
We define the twisted  -Bernoulli polynomials and the twisted generalized
-Bernoulli polynomials and the twisted generalized  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  of higher order and investigate some symmetric properties of them. Furthermore, using these symmetric properties of them, we can obtain some relationships between twisted
of higher order and investigate some symmetric properties of them. Furthermore, using these symmetric properties of them, we can obtain some relationships between twisted  -Bernoulli numbers and polynomials and between twisted generalized
-Bernoulli numbers and polynomials and between twisted generalized  -Bernoulli numbers and polynomials.
-Bernoulli numbers and polynomials.
1. Introduction
Let  be a fixed prime number. Throughout this paper
be a fixed prime number. Throughout this paper  , and
, and  will, respectively, denote the ring of
will, respectively, denote the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, and the completion of algebraic closure of
-adic rational numbers, and the completion of algebraic closure of  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  When one talks of
When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex number
is variously considered as an indeterminate, a complex number  or a
or a  -adic number
-adic number  . If
. If  one normally assumes
one normally assumes  If
If  then we assume
then we assume  so that
so that  for
for  (cf. [1–32]).
(cf. [1–32]).
For  , we set
, we set

(see [1–13]). The Bernoulli numbers  and polynomials
and polynomials  are defined by the generating function as
are defined by the generating function as


(cf. [17, 18, 21, 24, 26]). Let  be the set of uniformly differentiable functions on
be the set of uniformly differentiable functions on  . For
. For  , the
, the  -adic invariant integral on
-adic invariant integral on  is defined as
is defined as

Note that  (see [27]). Let
(see [27]). Let  be a translation with
be a translation with  . We note that
. We note that

(cf. [1–32]). Kim [18] studied the symmetric properties of the  -Bernoulli numbers and polynomials as follows:
-Bernoulli numbers and polynomials as follows:

In this paper, we define the twisted  -Bernoulli polynomials and the twisted generalized
-Bernoulli polynomials and the twisted generalized  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  of higher order and investigate some symmetric properties of them. Furthermore, using these symmetric properties of them, we can obtain some relationships between the twisted
of higher order and investigate some symmetric properties of them. Furthermore, using these symmetric properties of them, we can obtain some relationships between the twisted  -Bernoulli numbers and polynomials and between the twisted generalized
-Bernoulli numbers and polynomials and between the twisted generalized  -Bernoulli numbers and polynomials attached to
-Bernoulli numbers and polynomials attached to  of higher order.
of higher order.
2. The Twisted 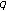 -Bernoulli Polynomials
-Bernoulli Polynomials
Let  be the locally constant space, where
be the locally constant space, where  is the cyclic group of order
is the cyclic group of order  . For
. For  , we denote the locally constant function by
, we denote the locally constant function by

(cf. [2, 3, 21, 24]). If we take  , then
, then

Now we define the  -extension of twisted Bernoulli numbers and polynomials as follows:
-extension of twisted Bernoulli numbers and polynomials as follows:


(see [31]). From (1.5), (2.2), (2.3), and (2.4), we can derive

By (1.5), we can see that

In (1.4), it is easy to show that

For each integer  , let
, let

From (2.6), (2.7), and (2.8), we derive

From (2.9), we note that

for all  . Let
. Let  ; then we have
; then we have

By (2.9), we see that

Let  be as follows:
be as follows:

Then we have

From (2.13), we derive

By (2.4), (2.12), and (2.15), we can see that

By the symmetry of  -adic invariant integral on
-adic invariant integral on  , we also see that
, we also see that

By comparing the coefficients of  on both sides of (2.16) and (2.17), we obtain the following theorem.
on both sides of (2.16) and (2.17), we obtain the following theorem.
Theorem 2.1.
Let  . Then for all
. Then for all  ,
,

where  is the binomial coefficient.
is the binomial coefficient.
From Theorem 2.1, if we take  , then we have the following corollary.
, then we have the following corollary.
Corollary 2.2.
For  , one we has
, one we has

where  is the binomial coefficient.
is the binomial coefficient.
By (2.17), (2.18), and (2.19), we can see that

From the symmetry of  , we can also derive
, we can also derive

By comparing the coefficients of  on both sides of (2.20) and (2.21), we obtain the following theorem.
on both sides of (2.20) and (2.21), we obtain the following theorem.
Theorem 2.3.
For  ,
,  , we have
, we have

We note that by setting  in Theorem 2.3, we get the following multiplication theorem for the twisted
in Theorem 2.3, we get the following multiplication theorem for the twisted  -Bernoulli polynomials.
-Bernoulli polynomials.
Theorem 2.4.
For  ,
,  , one has
, one has

Remark 2.5.
[18], Kim suggested open questions related to finding symmetric properties for Carlitz  -Bernoulli numbers. In this paper, we give the symmetric property for
-Bernoulli numbers. In this paper, we give the symmetric property for  -Bernoulli numbers in the viewpoint to give the answer of Kim's open questions.
-Bernoulli numbers in the viewpoint to give the answer of Kim's open questions.
3. The Twisted Generalized Bernoulli Polynomials Attached to 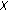 of Higher Order
of Higher Order
In this section, we consider the generalized Bernoulli numbers and polynomials and then define the twisted generalized Bernoulli polynomials attached to  of higher order by using multivariate
of higher order by using multivariate  -adic invariant integrals on
-adic invariant integrals on  . Let
. Let  be Dirichlet's character with conductor
be Dirichlet's character with conductor  . Then the generalized Bernoulli numbers
. Then the generalized Bernoulli numbers  and polynomials
and polynomials  attached to
attached to  are defined as
are defined as


Let  be the locally constant space, where
be the locally constant space, where  is the cyclic group of order
is the cyclic group of order  . For
. For  , we denote the locally constant function by
, we denote the locally constant function by

(cf. [2, 3, 21, 23, 24]). If we take  , for
, for  with
with  , then it is obvious from (3.1) that
, then it is obvious from (3.1) that

Now we define the twisted generalized Bernoulli numbers  and polynomials
and polynomials  attached to
attached to  as follows:
as follows:


for each  (see [31, 32]). By (3.5) and (3.6),
(see [31, 32]). By (3.5) and (3.6),

Thus we have

Then

Let us define the  -adic twisted
-adic twisted  -function
-function  as follows:
as follows:

By (3.9) and (3.10), we see that

Thus,

for all  . This means that
. This means that

for all  . For all
. For all  , we have
, we have

The twisted generalized Bernoulli numbers  and polynomials
and polynomials  attached to
attached to  of order
of order  are defined as
are defined as


for each  . For
. For  , we set
, we set

where  . In (3.17), we note that
. In (3.17), we note that  is symmetric in
is symmetric in  . From (3.17), we have
. From (3.17), we have

Thus we can obtain

From (3.19), we derive

By the symmetry of  in
in  and
and  , we can see that
, we can see that

By comparing the coefficients on both sides of (3.20) and (3.21), we see the following theorem.
Theorem 3.1.
For  ,
,  , one has
, one has

Remark 3.2.
If we take  and
and  in (3.22), then we have
in (3.22), then we have

Now we can also calculate

From the symmetric property of  in
in  and
and  , we derive
, we derive

By comparing the coefficients on both sides of (3.24) and (3.26), we obtain the following theorem.
Theorem 3.3.
For  ,
,  , we have
, we have

Remark 3.4.
If we take  and
and  in (3.26), then one has
in (3.26), then one has

Remark 3.5.
In our results for  , we can also derive similar results, which were treated in [27]. In this paper, we used the
, we can also derive similar results, which were treated in [27]. In this paper, we used the  -adic integrals to derive the symmetric properties of the
-adic integrals to derive the symmetric properties of the  -Bernoulli polynomials. By using the symmetric properties of
-Bernoulli polynomials. By using the symmetric properties of  -adic integral on
-adic integral on  , we can easily derive many interesting symmetric properties related to Bernoulli numbers and polynomials.
, we can easily derive many interesting symmetric properties related to Bernoulli numbers and polynomials.
References
Cenkci M, Simsek Y, Kurt V:Further remarks on multiple
 -adic
-adic  -
- -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.Jang L-C:On a
 -analogue of the
-analogue of the  -adic generalized twisted
-adic generalized twisted  -functions and
-functions and  -adic
-adic  -integrals. Journal of the Korean Mathematical Society 2007,44(1):1-10. 10.4134/JKMS.2007.44.1.139
-integrals. Journal of the Korean Mathematical Society 2007,44(1):1-10. 10.4134/JKMS.2007.44.1.139Jang L-C:Multiple twisted
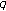 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 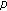 -adic
-adic 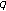 -integrals. Advances in Difference Equations 2008, 2008:-11.
-integrals. Advances in Difference Equations 2008, 2008:-11.Jang L-C, Kim S-D, Park D-W, Ro Y-S: A note on Euler number and polynomials. Journal of Inequalities and Applications 2006, 2006:-5.
Jang L-C, Kim T:On the distribution of the
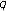 -Euler polynomials and the
-Euler polynomials and the  -Genocchi polynomials of higher order. Journal of Inequalities and Applications 2008, 2008:-9.
-Genocchi polynomials of higher order. Journal of Inequalities and Applications 2008, 2008:-9.Kim T:
 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.Kim T: On Euler-Barnes multiple zeta functions. Russian Journal of Mathematical Physics 2003,10(3):261-267.
Kim T:Analytic continuation of multiple
 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.Kim T:Power series and asymptotic series associated with the
 -analog of the two-variable
-analog of the two-variable  -adic
-adic 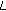 -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.Kim T:Multiple
 -adic
-adic 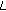 -function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038Kim T:A note on
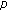 -Adic
-Adic 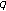 -integral on Zp associated with
-integral on Zp associated with  -Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.Kim T:On
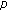 -adic interpolating function for
-adic interpolating function for 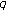 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027Kim T:On the analogs of Euler numbers and polynomials associated with
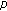 -adic
-adic 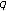 -integral on
-integral on  at
at 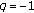 . Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027Kim T:A note on
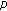 -adic
-adic 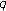 -integral on
-integral on 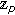 associated with
associated with  -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.Kim T:
 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3Kim T:A note on some formulae for the
 -Euler numbers and polynomials. Proc. Jangjeon Math. Soc. 2006,9(2):227-232.
-Euler numbers and polynomials. Proc. Jangjeon Math. Soc. 2006,9(2):227-232.Kim T:
 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.Kim T:On the symmetries of the
 -Bernoulli polynomials. Abstract and Applied Analysis 2008, 2008:-7.
-Bernoulli polynomials. Abstract and Applied Analysis 2008, 2008:-7.Kim T: Note on Dedekind type DC sums. Advanced Studies in Contemporary Mathematics 2009,18(2):249-260.
Kim T, Jang L-C, Pak HK:A note on
 -Euler and Genocchi numbers. Proceedings of the Japan Academy, Series A 2001,77(8):139-141. 10.3792/pjaa.77.139
-Euler and Genocchi numbers. Proceedings of the Japan Academy, Series A 2001,77(8):139-141. 10.3792/pjaa.77.139Kim T:Note on the
 -Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.
-Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.Kim T, Kim M-S, Jang L-C, Rim S-H:New
 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic  -integrals. Advanced Studies in Contemporary Mathematics 2007,15(2):243-252.
-integrals. Advanced Studies in Contemporary Mathematics 2007,15(2):243-252.Kim W, Kim Y-H, Jang L-C:On the
 -extension of apostol-euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.
-extension of apostol-euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.Simsek Y: Generating functions of the twisted Bernoulli numbers and polynomials associated with their interpolation functions. Advanced Studies in Contemporary Mathematics 2008,16(2):251-278.
Ozden H, Simsek Y, Rim S-H, Cangul IN:A note on
 -adic
-adic  -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.
-Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.Rim S-H, Kim Y-H, Lee BJ, Kim T: Some identities of the generalized twisted Bernoulli numbers and polynomials of higher order. Journal of Computational Analysis and Applications 2010, 12: 695-702.
Kim T:On a
 -analogue of the
-analogue of the 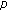 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373Kim T:Note on the Euler
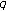 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007Kim T:A new approach to
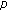 -adic
-adic 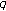 -
- -functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61-72.
-functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61-72.Kim T, Rim S-H:On the twisted
 -Euler numbers and polynomials associated with basic
-Euler numbers and polynomials associated with basic  -
- -functions. Journal of Mathematical Analysis and Applications 2007,336(1):738-744. 10.1016/j.jmaa.2007.03.035
-functions. Journal of Mathematical Analysis and Applications 2007,336(1):738-744. 10.1016/j.jmaa.2007.03.035Kim T:New approach to
 -Euler polynomials of higher order. Russian Journal of Mathematical Physics 2010,17(2):201-207. 10.1134/S1061920810020068
-Euler polynomials of higher order. Russian Journal of Mathematical Physics 2010,17(2):201-207. 10.1134/S1061920810020068Kim T:Barnes-type multiple
 -zeta functions and
-zeta functions and 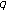 -Euler polynomials. Journal of Physics A 2010, 43:-11.
-Euler polynomials. Journal of Physics A 2010, 43:-11.
Acknowledgments
The authors express Their sincere gratitude to referees for their valuable suggestions and comments. This work has been conducted by the Research Grant of Kwangwoon University in 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jang, LC., Yi, H., Shivashankara, K. et al. A Note on Symmetric Properties of the Twisted  -Bernoulli Polynomials and the Twisted Generalized
-Bernoulli Polynomials and the Twisted Generalized  -Bernoulli Polynomials.
Adv Differ Equ 2010, 801580 (2010). https://doi.org/10.1155/2010/801580
-Bernoulli Polynomials.
Adv Differ Equ 2010, 801580 (2010). https://doi.org/10.1155/2010/801580
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/801580
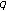 -Bernoulli Polynomials
-Bernoulli Polynomials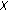 of Higher Order
of Higher Order -adic
-adic 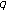 -
- -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68. -analogue of the
-analogue of the  -adic generalized twisted
-adic generalized twisted  -functions and
-functions and 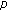 -adic
-adic  -integrals. Journal of the Korean Mathematical Society 2007,44(1):1-10. 10.4134/JKMS.2007.44.1.139
-integrals. Journal of the Korean Mathematical Society 2007,44(1):1-10. 10.4134/JKMS.2007.44.1.139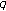 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 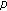 -adic
-adic 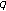 -integrals. Advances in Difference Equations 2008, 2008:-11.
-integrals. Advances in Difference Equations 2008, 2008:-11.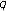 -Euler polynomials and the
-Euler polynomials and the 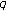 -Genocchi polynomials of higher order. Journal of Inequalities and Applications 2008, 2008:-9.
-Genocchi polynomials of higher order. Journal of Inequalities and Applications 2008, 2008:-9.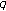 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.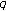 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.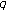 -analog of the two-variable
-analog of the two-variable  -adic
-adic 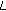 -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196. -adic
-adic 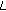 -function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038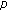 -Adic
-Adic 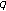 -integral on Zp associated with
-integral on Zp associated with  -Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.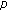 -adic interpolating function for
-adic interpolating function for 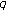 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027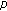 -adic
-adic 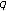 -integral on
-integral on  at
at 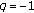 . Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027 -adic
-adic 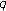 -integral on
-integral on 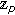 associated with
associated with 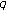 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137. -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3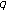 -Euler numbers and polynomials. Proc. Jangjeon Math. Soc. 2006,9(2):227-232.
-Euler numbers and polynomials. Proc. Jangjeon Math. Soc. 2006,9(2):227-232.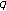 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57. -Bernoulli polynomials. Abstract and Applied Analysis 2008, 2008:-7.
-Bernoulli polynomials. Abstract and Applied Analysis 2008, 2008:-7.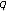 -Euler and Genocchi numbers. Proceedings of the Japan Academy, Series A 2001,77(8):139-141. 10.3792/pjaa.77.139
-Euler and Genocchi numbers. Proceedings of the Japan Academy, Series A 2001,77(8):139-141. 10.3792/pjaa.77.139 -Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.
-Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.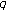 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 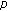 -adic
-adic  -integrals. Advanced Studies in Contemporary Mathematics 2007,15(2):243-252.
-integrals. Advanced Studies in Contemporary Mathematics 2007,15(2):243-252.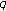 -extension of apostol-euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.
-extension of apostol-euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.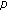 -adic
-adic  -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.
-Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239. -analogue of the
-analogue of the 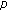 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320-329. 10.1006/jnth.1999.2373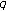 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007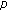 -adic
-adic  -
- -functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61-72.
-functions. Advanced Studies in Contemporary Mathematics 2006,12(1):61-72. -Euler numbers and polynomials associated with basic
-Euler numbers and polynomials associated with basic  -
- -functions. Journal of Mathematical Analysis and Applications 2007,336(1):738-744. 10.1016/j.jmaa.2007.03.035
-functions. Journal of Mathematical Analysis and Applications 2007,336(1):738-744. 10.1016/j.jmaa.2007.03.035 -Euler polynomials of higher order. Russian Journal of Mathematical Physics 2010,17(2):201-207. 10.1134/S1061920810020068
-Euler polynomials of higher order. Russian Journal of Mathematical Physics 2010,17(2):201-207. 10.1134/S1061920810020068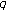 -zeta functions and
-zeta functions and 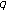 -Euler polynomials. Journal of Physics A 2010, 43:-11.
-Euler polynomials. Journal of Physics A 2010, 43:-11.