- Research Article
- Open access
- Published:
Asymptotical Convergence of the Solutions of a Linear Differential Equation with Delays
Advances in Difference Equations volume 2010, Article number: 749852 (2010)
Abstract
The asymptotic behavior of the solutions of the first-order differential equation  containing delays is studied with
containing delays is studied with  ,
,  ,
,  ,
,  . The attention is focused on an analysis of the asymptotical convergence of solutions. A criterion for the asymptotical convergence of all solutions, characterized by the existence of a strictly increasing bounded solution, is proved. Relationships with the previous results are discussed, too.
. The attention is focused on an analysis of the asymptotical convergence of solutions. A criterion for the asymptotical convergence of all solutions, characterized by the existence of a strictly increasing bounded solution, is proved. Relationships with the previous results are discussed, too.
1. Introduction
We investigate the asymptotic behavior of the solutions of a linear homogeneous differential equation with delayed terms

as  . In (1.1) we assume
. In (1.1) we assume  ,
,  , functions
, functions  where
where  ,
,  ,
,  are continuous and such that
are continuous and such that  on
on  . Set
. Set  . Throughout the paper the symbol "
. Throughout the paper the symbol " " denotes the right-hand derivative. Similarly, if necessary, the value of a function at a point of
" denotes the right-hand derivative. Similarly, if necessary, the value of a function at a point of  is understood as the value of the corresponding limit from the right.
is understood as the value of the corresponding limit from the right.
We call a solution  of (1.1) asymptotically convergent if it has a finite limit
of (1.1) asymptotically convergent if it has a finite limit  . The main results concern the asymptotical convergence of all solutions of (1.1). Besides, the proof of the results is based on the comparison of solutions of (1.1) with solutions of an auxiliary inequality which formally copies (1.1). At first, we prove that, under certain conditions, (1.1) has a strictly increasing asymptotically convergent solution. Then we extend this statement to all the solutions of (1.1). Moreover, in the general case, the asymptotical convergence of all solutions is characterized by the existence of a strictly increasing bounded solution.
. The main results concern the asymptotical convergence of all solutions of (1.1). Besides, the proof of the results is based on the comparison of solutions of (1.1) with solutions of an auxiliary inequality which formally copies (1.1). At first, we prove that, under certain conditions, (1.1) has a strictly increasing asymptotically convergent solution. Then we extend this statement to all the solutions of (1.1). Moreover, in the general case, the asymptotical convergence of all solutions is characterized by the existence of a strictly increasing bounded solution.
The problem concerning the asymptotical convergence of solutions of delayed differential equations (or delayed difference equation, etc.) is a classical one. But the problem of the asymptotic convergence or divergence of solutions of delayed equations receives permanent attention. Let us mention at least investigations [1–18]. Comparing the known investigations with the results presented we conclude that our results give more sharp sufficient conditions.
The paper is organized as follows. In Section 2 an auxiliary inequality is studied and the relationship of its solutions with solutions of (1.1) is derived. The existence of a strictly increasing and convergent solution of (1.1) is established in Section 3. Section 4 contains results concerning the asymptotical convergence of all the solutions of (1.1). The related previous results are discussed in Section 5.
Let  be the Banach space of continuous functions mapping the interval
be the Banach space of continuous functions mapping the interval  into
into  equipped with the supremum norm.
equipped with the supremum norm.
Let  be given. The function
be given. The function  is said to be a solution of (1.1) on
is said to be a solution of (1.1) on if
if  is continuous on
is continuous on  , continuously differentiable on
, continuously differentiable on  and satisfies (1.1) for
and satisfies (1.1) for  .
.
For  ,
,  , we say that
, we say that  is a solution of (1.1) through
is a solution of (1.1) through (or that
(or that  corresponds to the initial point
corresponds to the initial point ) if
) if  is a solution of (1.1) on
is a solution of (1.1) on  and
and  for
for  .
.
2. Auxiliary Inequality
The inequality

plays an important role in the analysis of (1.1). Let  and
and  be given. The function
be given. The function  is said to be a solution of (2.1) on
is said to be a solution of (2.1) on if
if  is continuous on
is continuous on  , continuously differentiable on
, continuously differentiable on  , and satisfies inequality (2.1) for
, and satisfies inequality (2.1) for  . If
. If  , we call the solution
, we call the solution  of (2.1) asymptotically convergent if it has a finite limit
of (2.1) asymptotically convergent if it has a finite limit  .
.
2.1. Relationship between the Solutions of Inequality (2.1) and Equation (1.1)
In this part, we will derive some properties of the solutions of type (2.1) inequalities and compare the solutions of (1.1) with those of inequality (2.1).
Lemma 2.1.
Let  be strictly increasing (nondecreasing, strictly decreasing, nonincreasing) on
be strictly increasing (nondecreasing, strictly decreasing, nonincreasing) on  . Then the corresponding solution
. Then the corresponding solution  of (1.1) with
of (1.1) with  is strictly increasing (nondecreasing, strictly decreasing, nonincreasing) on
is strictly increasing (nondecreasing, strictly decreasing, nonincreasing) on  , respectively. If
, respectively. If  is strictly increasing (nondecreasing) and
is strictly increasing (nondecreasing) and  is a solution of (2.1) with
is a solution of (2.1) with  ,
,  , then
, then  is strictly increasing (nondecreasing) on
is strictly increasing (nondecreasing) on  .
.
Proof.
This is clear from (1.1) and (2.1) and from  ,
,  ,
,  ,
,  ,
,  .
.
Theorem 2.2.
Let  be a solution of inequality (2.1) on
be a solution of inequality (2.1) on  . Then there exists a solution
. Then there exists a solution  of (1.1) on
of (1.1) on  such that the inequality
such that the inequality

holds on  . In particular, a solution
. In particular, a solution  of (1.1) with
of (1.1) with  defined by the relation
defined by the relation

is such a solution.
Proof.
Let  be a solution of inequality (2.1) on
be a solution of inequality (2.1) on  . We will show that the solution
. We will show that the solution  of (1.1) satisfies inequality (2.2), that is,
of (1.1) satisfies inequality (2.2), that is,

on  . Define on
. Define on  the continuous function
the continuous function  . Then
. Then  on
on  , and
, and  is a solution of (2.1) on
is a solution of (2.1) on  . Lemma 2.1 implies that
. Lemma 2.1 implies that  is nondecreasing. Consequently,
is nondecreasing. Consequently,  for all
for all  .
.
Remark 2.3.
Let us note that the assertion, opposite in a sense with to that statement of Theorem 2.2, is obvious. Namely, if a solution  of (1.1) on
of (1.1) on  is given, then there exists a solution
is given, then there exists a solution  of inequality ( 2.1 ) on
of inequality ( 2.1 ) on  such that the inequality
such that the inequality

holds on  since it can be put
since it can be put  . Moreover, if we put, for example,
. Moreover, if we put, for example,  , then
, then

on  .
.
2.2. A Solution of Inequality (2.1)
It is easy to get a solution of inequality (2.1) in an exponential form. We will indicate this form in the following lemma. This auxiliary result will help us derive concrete sufficient conditions for the existence of strictly increasing and convergent solution of (1.1).
Lemma 2.4.
Let there exist a function  , continuous on
, continuous on  with at most first-order discontinuity at the point
with at most first-order discontinuity at the point  and satisfying the inequality
and satisfying the inequality

on  . Then there exists a solution
. Then there exists a solution  of inequality (2.1), defined on
of inequality (2.1), defined on  , and having the form
, and having the form

Proof.
Inequality (2.7) follows immediately from inequality (2.1) for  .
.
3. Existence of an Asymptotically Convergent Solution of (1.1)
In this part we indicate sufficient conditions for the existence of a convergent solution of (1.1). First, let us introduce two obvious statements concerning asymptotical convergence. From Theorem 2.2 and Lemma 2.1, we immediately get the following.
Theorem 3.1.
If  is a strictly increasing asymptotically convergent solution of (2.1) on
is a strictly increasing asymptotically convergent solution of (2.1) on  , then there exists a strictly increasing asymptotically convergent solution
, then there exists a strictly increasing asymptotically convergent solution  of (1.1) on
of (1.1) on  .
.
From Lemma 2.1, Theorem 2.2, and Lemma 2.4, we get the following.
Theorem 3.2.
If there exists a function  , continuous on
, continuous on  with at most the first order discontinuity at the point
with at most the first order discontinuity at the point  satisfying
satisfying  , and the inequality (2.7) on
, and the inequality (2.7) on  , the initial function
, the initial function

defines a strictly increasing and asymptotically convergent solution  of (1.1) on
of (1.1) on  satisfying the inequality
satisfying the inequality

on  .
.
Theorem 3.3.
If there exists a constant  such that
such that

there exists a strictly increasing and asymptotically convergent solution  of (1.1) as
of (1.1) as  .
.
Proof.
Let us verify that the integral inequality (2.7) has (for every sufficiently large  ) a solution
) a solution  such that
such that

In inequality (2.7), we put

where  . Then (3.4) holds. Now we perform an auxiliary asymptotical analysis for
. Then (3.4) holds. Now we perform an auxiliary asymptotical analysis for  . The symbol
. The symbol  used below is the Landau order symbol. All asymptotical decompositions are developed with sufficient accuracy. Let
used below is the Landau order symbol. All asymptotical decompositions are developed with sufficient accuracy. Let  be a nonzero constant. Then
be a nonzero constant. Then

Moreover

We use the asymptotical decomposition (3.7) and rewrite the integral inequality (2.7). We get

or

Multiplying this inequality by  , we get
, we get

Analysing inequality (3.10), we conclude that the inequality

or, equivalently,

is a necessary condition for its validity as  (because
(because  and
and  ,
,  ). Consequently,
). Consequently,

Then, inequality (3.10) will be valid as  if there exist positive constants
if there exist positive constants  and
and  such that
such that

Inequality (3.3) implies that there is a positive constant  such that
such that

Finally, since

as  , we conclude that (3.14) holds and, consequently, the integral inequality (2.7) has a solution
, we conclude that (3.14) holds and, consequently, the integral inequality (2.7) has a solution  for every sufficiently large
for every sufficiently large  . Lemma 2.4 holds. We finalize the proof by noticing that the statement of the theorem directly follows from Theorem 3.1.
. Lemma 2.4 holds. We finalize the proof by noticing that the statement of the theorem directly follows from Theorem 3.1.
Assuming that functions  ,
,  ,
,  can be estimated by suitable functions, we will prove that (1.1) has an asymptotically convergent solution. This yields two interesting corollaries directly following from inequality (3.3) in Theorem 3.3.
can be estimated by suitable functions, we will prove that (1.1) has an asymptotically convergent solution. This yields two interesting corollaries directly following from inequality (3.3) in Theorem 3.3.
Corollary 3.4.
Let

where  and
and  are nonnegative constants and
are nonnegative constants and  on
on  . If, moreover,
. If, moreover,

then there exists a strictly increasing and convergent solution  of (1.1) as
of (1.1) as  .
.
Proof.
We show that the inequality (3.3) in Theorem 3.3 holds for any  . Estimating the left-hand side of (3.3), we get
. Estimating the left-hand side of (3.3), we get

since  .
.
Corollary 3.5.
Let

where  and
and  are nonnegative constants and
are nonnegative constants and  on
on  . If, moreover,
. If, moreover,

and there exists a constant  such that
such that

then there exists a strictly increasing and convergent solution  of (1.1) as
of (1.1) as  .
.
Proof.
Employing a part of the proof of Corollary 3.4 with  , we use inequality (3.22). Then
, we use inequality (3.22). Then

Thus, the inequality (3.3) in Theorem 3.3 holds.
4. Asymptotical Convergence of All Solutions
In this part we prove results concerning the asymptotical convergence of all the solutions of (1.1). First, we use inequality (3.3) to establish conditions for the asymptotical convergence of all the solutions.
Theorem 4.1.
Let there exist  such that inequality (3.3) holds. Then all the solutions of (1.1) are asymptotically convergent for
such that inequality (3.3) holds. Then all the solutions of (1.1) are asymptotically convergent for  .
.
Proof.
First we prove that every solution defined by a monotone initial function is asymptotically convergent. We will assume that a monotone initial function  is given. For the definiteness, let
is given. For the definiteness, let  be strictly increasing or nondecreasing (the strictly decreasing or nonincreasing case can be dealt with in much the same way). By Lemma 2.1, the solution
be strictly increasing or nondecreasing (the strictly decreasing or nonincreasing case can be dealt with in much the same way). By Lemma 2.1, the solution  is monotone (either strictly increasing or nondecreasing) on
is monotone (either strictly increasing or nondecreasing) on  . In what follows, we will prove that
. In what follows, we will prove that  is asymptotically convergent.
is asymptotically convergent.
By Theorem 3.3, there exists a strictly increasing and asymptotically convergent solution  of (1.1) on
of (1.1) on  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  on
on  since, in the opposite case, we can choose another initial function. Moreover, we can assume that both solutions
since, in the opposite case, we can choose another initial function. Moreover, we can assume that both solutions  and
and  are continuously differentiable on
are continuously differentiable on  . In the opposite case, we can start our reasoning with the interval
. In the opposite case, we can start our reasoning with the interval  instead of
instead of  , that is, we can replace
, that is, we can replace  by
by  and
and  by
by  . Similarly, without loss of generality we can assume that
. Similarly, without loss of generality we can assume that  ,
,  . Hence, there is a
. Hence, there is a  such that
such that

Then, by Lemma 2.1,  is strictly increasing in
is strictly increasing in  . Thus
. Thus

is a bounded function for all  .
.
Summarizing the previous part, we state that every monotone solution is asymptotically convergent. It remains to consider a class of all nonmonotone initial functions. For the behavior of a solution  , generated by a nonmonotone initial function
, generated by a nonmonotone initial function  there are two possibilities: either
there are two possibilities: either  is eventually monotone and, consequently, asymptotically convergent, or
is eventually monotone and, consequently, asymptotically convergent, or  is eventually nonmonotone.
is eventually nonmonotone.
We will also use the known fact that every absolutely continuous function can be decomposed into the difference of two strictly increasing absolutely continuous functions [19, page 315]. Assuming that an initial (nonmonotone) function  is absolutely continuous on interval
is absolutely continuous on interval  , we can decompose it on the interval
, we can decompose it on the interval  into the difference
into the difference  of two strictly increasing absolutely continuous functions
of two strictly increasing absolutely continuous functions  ,
,  . In accordance with the previous part of the proof, every function
. In accordance with the previous part of the proof, every function  ,
,  defines a strictly increasing convergent solution
defines a strictly increasing convergent solution  . Now it becomes clear that the solution
. Now it becomes clear that the solution  is asymptotically convergent. To complete the proof, it remains to prove that, without loss of generality, we can restrict the set of all initial functions to the set of absolutely continuous initial functions. To this end, we again consider the solution
is asymptotically convergent. To complete the proof, it remains to prove that, without loss of generality, we can restrict the set of all initial functions to the set of absolutely continuous initial functions. To this end, we again consider the solution  defined by
defined by  and, if necessary, always without loss of generality, we can replace
and, if necessary, always without loss of generality, we can replace  by
by  and
and  by
by  since the solution has a finite derivative the interval
since the solution has a finite derivative the interval  . Finally, we remark that any function satisfying the Lipschitz condition on an interval
. Finally, we remark that any function satisfying the Lipschitz condition on an interval  is absolutely continuous in it [19, page 313].
is absolutely continuous in it [19, page 313].
Tracing the proof of Theorem 4.1, we can see that the inequality (3.3) was used only as "input" information stating that, in accordance with Theorem 3.3, there exists a strictly increasing and asymptotically convergent solution  of (1.1) on
of (1.1) on  . If the existence of a strictly monotone and asymptotically convergent solution is assumed instead of (3.3), we obtain the following
. If the existence of a strictly monotone and asymptotically convergent solution is assumed instead of (3.3), we obtain the following
Theorem 4.2.
If (1.1) has a strictly monotone and convergent solution on  , then all the solutions of (1.1) defined on
, then all the solutions of (1.1) defined on  are asymptotically convergent.
are asymptotically convergent.
Moreover, combining the results formulated in Theorems 2.2, 3.1 and 4.2, we obtain the following
Theorem 4.3.
The following three statements are equivalent.
-
(a)
Equation (1.1) has a strictly monotone and asymptotically convergent solution on
 .
. -
(b)
All solutions of (1.1) defined on
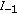 are asymptotically convergent.
are asymptotically convergent. -
(c)
Inequality (2.1) has a strictly monotone and asymptotically convergent solution on
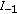 .
.
5. Comparison with Previous Results
In [8], conditions for the asymptotical convergence of all the solutions of (1.1) with  and
and  , that is,
, that is,

are given. A particular case of (1.1) with  , that is, the case
, that is, the case

is treated, for example, in [2, 4, 10, 11]. The following theorem (see [11, Theorems  ,
,  , and
, and  ]) gives corresponding results related to (5.2). Its first part gives sufficient conditions for the existence of a strictly increasing and unbounded solution of (5.2) whereas the second part provides sufficient conditions for the asymptotical convergence of all its solutions.
]) gives corresponding results related to (5.2). Its first part gives sufficient conditions for the existence of a strictly increasing and unbounded solution of (5.2) whereas the second part provides sufficient conditions for the asymptotical convergence of all its solutions.
Theorem 5.1.
-
(a)
Let there exist a constant
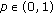 such that the inequality
such that the inequality 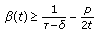 (5.3)
(5.3)
holds for all  . Then there exists a strictly increasing and unbounded solution of (5.2) as
. Then there exists a strictly increasing and unbounded solution of (5.2) as  .
.
-
(b)
Let there exist a constant
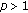 such that the inequality
such that the inequality 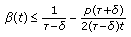 (5.4)
(5.4)
holds for all  . Then all solutions of (5.2) defined on
. Then all solutions of (5.2) defined on  are convergent.
are convergent.
Comparing (5.3) with (5.4), we see that the maximal allowed values for  given in (5.4) are not strictly opposite with respect to the minimal allowed values for
given in (5.4) are not strictly opposite with respect to the minimal allowed values for  given in (5.3). This is a gap since
given in (5.3). This is a gap since

and one would expect a pair of opposite inequalities stronger than (5.3) and (5.4). Can one of the inequalities (5.3) or (5.4) be improved? The following example shows that probably (5.3) can be improved because (5.4) provides a best possible criterion.
Example 5.2.
Consider (5.2) with  , that is,
, that is,

It is easy to verify that  is a strictly increasing and unbounded solution of (5.6) as
is a strictly increasing and unbounded solution of (5.6) as  . Decomposing asymptotically
. Decomposing asymptotically  as
as  we get
we get

We conclude that this function can satisfy the inequality (5.4) as  , that is, the inequality
, that is, the inequality

only if  .
.
References
Arino O, Pituk M: Convergence in asymptotically autonomous functional-differential equations. Journal of Mathematical Analysis and Applications 1999,237(1):376-392. 10.1006/jmaa.1999.6489
Arino O, Pituk M: More on linear differential systems with small delays. Journal of Differential Equations 2001,170(2):381-407. 10.1006/jdeq.2000.3824
Atkinson FV, Haddock JR: Criteria for asymptotic constancy of solutions of functional-differential equations. Journal of Mathematical Analysis and Applications 1983,91(2):410-423. 10.1016/0022-247X(83)90161-0
Bereketoğlu H, Pituk M: Asymptotic constancy for nonhomogeneous linear differential equations with unbounded delays. Discrete and Continuous Dynamical Systems. Series A 2003,2003(supplement):100-107.
Čermák J: Asymptotic bounds for linear difference systems. Advances in Difference Equations 2010, 2010:-14.
Čermák J: On matrix differential equations with several unbounded delays. European Journal of Applied Mathematics 2006,17(4):417-433. 10.1017/S0956792506006590
Čermák J, Kundrát P: Linear differential equations with unbounded delays and a forcing term. Abstract and Applied Analysis 2004, (4):337-345.
Diblík J: Asymptotic convergence criteria of solutions of delayed functional differential equations. Journal of Mathematical Analysis and Applications 2002,274(1):349-373. 10.1016/S0022-247X(02)00311-6
Diblík J:Asymptotic representation of solutions of equation
 . Journal of Mathematical Analysis and Applications 1998,217(1):200-215. 10.1006/jmaa.1997.5709
. Journal of Mathematical Analysis and Applications 1998,217(1):200-215. 10.1006/jmaa.1997.5709Diblík J, Růžičková M:Exponential solutions of equation
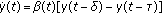 . Journal of Mathematical Analysis and Applications 2004,294(1):273-287. 10.1016/j.jmaa.2004.02.036
. Journal of Mathematical Analysis and Applications 2004,294(1):273-287. 10.1016/j.jmaa.2004.02.036Diblík J, Růžičková M:Convergence of the solutions of the equation
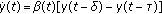 in the critical case. Journal of Mathematical Analysis and Applications 2007,331(2):1361-1370. 10.1016/j.jmaa.2006.10.001
in the critical case. Journal of Mathematical Analysis and Applications 2007,331(2):1361-1370. 10.1016/j.jmaa.2006.10.001Dorociaková B, Olach R: Existence of positive solutions of delay differential equations. Tatra Mountains Mathematical Publications 2009, 43: 63-70.
Györi I, Horvath L: Asymptotic constancy in linear difference equations: limit formulae and sharp conditions. Advances in Difference Equations 2010, 2010:-20.
Györi I, Pituk M: Comparison theorems and asymptotic equilibrium for delay differential and difference equations. Dynamic Systems and Applications 1996,5(2):277-302.
Hanuštiaková L, Olach R: Nonoscillatory bounded solutions of neutral differential systems. Nonlinear Analysis 2008,68(7):1816-1824. 10.1016/j.na.2007.01.014
Krisztin T: A note on the convergence of the solutions of a linear functional-differential equation. Journal of Mathematical Analysis and Applications 1990,145(1):17-25. 10.1016/0022-247X(90)90427-H
Murakami K: Asymptotic constancy for systems of delay differential equations. Nonlinear Analysis 1997,30(7):4595-4606. 10.1016/S0362-546X(97)00316-7
Šmarda Z: Singular cauchy initial value problem for certain classes of integro-differential equations. Advances in Difference Equations 2010, 2010:-13.
Vulich BZ: Short Course of Theory of Functions of a Real Variable, An Introduction to the Integral Theory. 2nd edition. Nauka, Moscow, Russia; 1973.
Acknowledgments
This research was supported by the Grant no. 1/0090/09 of the Grant Agency of Slovak Republic (VEGA) and by the project APVV-0700-07 of Slovak Research and Development Agency.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Diblík, J., Růžičková, M. & Šutá, Z. Asymptotical Convergence of the Solutions of a Linear Differential Equation with Delays. Adv Differ Equ 2010, 749852 (2010). https://doi.org/10.1155/2010/749852
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/749852
 .
.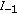 are asymptotically convergent.
are asymptotically convergent.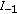 .
.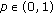 such that the inequality
such that the inequality 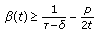
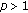 such that the inequality
such that the inequality 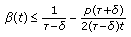
 . Journal of Mathematical Analysis and Applications 1998,217(1):200-215. 10.1006/jmaa.1997.5709
. Journal of Mathematical Analysis and Applications 1998,217(1):200-215. 10.1006/jmaa.1997.5709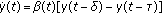 . Journal of Mathematical Analysis and Applications 2004,294(1):273-287. 10.1016/j.jmaa.2004.02.036
. Journal of Mathematical Analysis and Applications 2004,294(1):273-287. 10.1016/j.jmaa.2004.02.036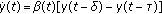 in the critical case. Journal of Mathematical Analysis and Applications 2007,331(2):1361-1370. 10.1016/j.jmaa.2006.10.001
in the critical case. Journal of Mathematical Analysis and Applications 2007,331(2):1361-1370. 10.1016/j.jmaa.2006.10.001