- Research Article
- Open access
- Published:
A Note on a Semilinear Fractional Differential Equation of Neutral Type with Infinite Delay
Advances in Difference Equations volume 2010, Article number: 674630 (2010)
Abstract
We deal in this paper with the mild solution for the semilinear fractional differential equation of neutral type with infinite delay:  ,
,  ,
,  ,
,  , with
, with  and
and  . We prove the existence (and uniqueness) of solutions, assuming that
. We prove the existence (and uniqueness) of solutions, assuming that  is a linear closed operator which generates an analytic semigroup
is a linear closed operator which generates an analytic semigroup  on a Banach space
on a Banach space  by means of the Banach's fixed point theorem. This generalizes some recent results.
by means of the Banach's fixed point theorem. This generalizes some recent results.
1. Introduction
We investigate in this paper the existence and uniqueness of the mild solution for the fractional differential equation with infinite delay

where 

 is a generator of an analytic semigroup
is a generator of an analytic semigroup  on a Banach space
on a Banach space  such that
such that  for all
for all  and
and  for every
for every  and
and  . The function
. The function  is continuous functions with additional assumptions.
is continuous functions with additional assumptions.
The fractional derivative  is understood here in the Caputo sense, that is,
is understood here in the Caputo sense, that is,

 where
where  is called phase space to be defined in Section 2. For any function
is called phase space to be defined in Section 2. For any function  defined on
defined on  and any
and any  , we denote by
, we denote by  the element of
the element of  defined by
defined by

The function  represents the history of the state from
represents the history of the state from  up to the present time
up to the present time  .
.
The theory of functional differential equations has emerged as an important branch of nonlinear analysis. It is worthwhile mentioning that several important problems of the theory of ordinary and delay differential equations lead to investigations of functional differential equations of various types (see the books by Hale and Verduyn Lunel [1], Wu [2], Liang et al. [3], Liang and Xiao [4–9], and the references therein). On the other hand the theory of fractional differential equations is also intensively studied and finds numerous applications in describing real world problems (see e.g., the monographs of Lakshmikantham et al. [10], Lakshmikantham [11], Lakshmikantham and Vatsala [12, 13], Podlubny [14], and the papers of Agarwal et al. [15], Benchohra et al. [16], Anguraj et al. [17], Mophou and N'Guérékata [18], Mophou et al. [19], Mophou and N'Guérékata [20], and the references therein).
Recently we studied in our paper [20] the existence of solutions to the fractional semilinear differential equation with nonlocal condition and delay-free

where  is a positive real,
is a positive real, 
 is the generator of a
is the generator of a  -semigroup
-semigroup  on a Banach space
on a Banach space 
 ,
,  with
with  defined as above and
defined as above and

 is a nonlinear function,
is a nonlinear function,  is continuous, and
is continuous, and  . The derivative
. The derivative  is understood here in the Riemann-Liouville sense.
is understood here in the Riemann-Liouville sense.
In the present paper we deal with an infinite time delay. Note that in this case, the phase space  plays a crucial role in the study of both qualitative and quantitative aspects of theory of functional equations. Its choice is determinant as can be seen in the important paper by Hale and Kato [21].
plays a crucial role in the study of both qualitative and quantitative aspects of theory of functional equations. Its choice is determinant as can be seen in the important paper by Hale and Kato [21].
Similar works to the present paper include the paper by Benchohra et al. [16], where the authors studied an existence result related to the nonlinear functional differential equation

where  is the standard Riemann-Liouville fractional derivative,
is the standard Riemann-Liouville fractional derivative,  in the phase space
in the phase space  , with
, with  .
.
2. Preliminaries
From now on, we set  . We denote by
. We denote by  a Banach space with norm
a Banach space with norm  ,
,  the space of all
the space of all  -valued continuous functions on
-valued continuous functions on  , and
, and  the Banach space of all linear and bounded operators on
the Banach space of all linear and bounded operators on  .
.
We assume that the phase space  is a seminormed linear space of functions mapping
is a seminormed linear space of functions mapping  into
into  , and satisfying the following fundamental axioms due to Hale and Kato (see e.g., in [21]).
, and satisfying the following fundamental axioms due to Hale and Kato (see e.g., in [21]).
If  , is continuous on
, is continuous on  and
and  , then for every
, then for every  the following conditions hold:
the following conditions hold:
-
(i)
 is in
is in 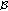 ,
, -
(ii)

-
(iii)
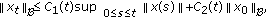
where  is a constant,
is a constant,  is continuous,
is continuous,  is locally bounded, and
is locally bounded, and  ,
,  ,
,  are independent of
are independent of  .
.
For the function  in
in  ,
,  is a
is a  -valued continuous function on
-valued continuous function on  .
.
The space  is complete.
is complete.
Remark.
Condition (ii) in  is equivalent to
is equivalent to  for all
for all  .
.
Let us recall some examples of phase spaces.
Example.
(E1)  the Banach space of all bounded and uniformly continuous functions
the Banach space of all bounded and uniformly continuous functions  endowed with the supnorm.
endowed with the supnorm.
(E2)  the Banach space of all bounded and continuous functions
the Banach space of all bounded and continuous functions  such that
such that  endowed with the norm
endowed with the norm

( )
) endowed with the norm
endowed with the norm

Note that the space  is a uniform fading memory for
is a uniform fading memory for  .
.
Throughout this work  will be a continuous function
will be a continuous function  . Let
. Let  be set defined by:
be set defined by:

Remark.
We recall that the Cauchy Problem

where  is a closed linear operator defined on a dense subset,
is a closed linear operator defined on a dense subset,  is wellposed, and the unique solution is given by
is wellposed, and the unique solution is given by

where  is a probability density function defined on
is a probability density function defined on  such that its Laplace transform is given by
such that its Laplace transform is given by

([22, cf. Theorem 2.1]).
Following [22, 23] we will introduce now the definition of mild solution to (1.1).
Definition 2.4.
A function  is said to be a mild solution of (1.1) if
is said to be a mild solution of (1.1) if  satisfies
satisfies

where

Remark 2.5.
Note that

since  (cf. [23]).
(cf. [23]).
3. Main Results
We present now our result.
Theorem 3.1.
Assume the following.
-
(H1) There exist
 such that for all
such that for all  ,
, 
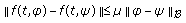 (3.1)
(3.1) -
(H2) There exists
 , with
, with  such that the function
such that the function 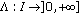 defined by:
defined by:

satisfies  for all
for all  . Here
. Here

Then (1.1) has a unique mild solution on  .
.
Proof.
Consider the operator  defined by
defined by

Let  be the function defined by
be the function defined by

Then  . For each
. For each  with
with  , we denote by
, we denote by  the function defined by
the function defined by

If  verifies (2.7) then writing
verifies (2.7) then writing  for
for  , we have
, we have  for
for  and
and

Moreover  .
.
Let

For any  , we have
, we have

Thus  is a Banach space. We define the operator
is a Banach space. We define the operator  by
by

It is clear that the operator  has a unique fixed point if and only if
has a unique fixed point if and only if  has a unique fixed point. So let us prove that
has a unique fixed point. So let us prove that  has a unique fixed point. Observe first that
has a unique fixed point. Observe first that  is obviously well defined. Now, consider
is obviously well defined. Now, consider  . For any
. For any  , we have
, we have

So using  , (2.9) and (3.3), we obtain for all
, (2.9) and (3.3), we obtain for all 

which according to  gives
gives

Therefore

And since  , we conclude by way of the Banach's contraction mapping principle that
, we conclude by way of the Banach's contraction mapping principle that  has a unique fixed point
has a unique fixed point  . This means that
. This means that  has a unique fixed point
has a unique fixed point  which is obviously a mild solution of (1.1) on
which is obviously a mild solution of (1.1) on  .
.
4. Application
To illustrate our result, we consider the following Lotka-Volterra model with diffusion:

where  and
and  is a positive function on
is a positive function on  with
with  .
.
Now let  and consider the operator
and consider the operator  defined by
defined by

Clearly  is dense in
is dense in  .
.
Define

We choose  as in Example (E3) above. Put
as in Example (E3) above. Put

Then we get

where  is obviously Lipschitzian in
is obviously Lipschitzian in  uniformly in
uniformly in  . Thus we can state what follows.
. Thus we can state what follows.
Theorem 4.1.
Under the above assumptions (4.1) has a unique mild solution.
References
Hale JK, Verduyn Lunel SM: Introduction to Functional-Differential Equations, Applied Mathematical Sciences. Volume 99. Springer, New York, NY, USA; 1993:x+447.
Wu J: Theory and Applications of Partial Functional-Differential Equations, Applied Mathematical Sciences. Volume 119. Springer, New York, NY, USA; 1996:x+429.
Liang J, Huang F, Xiao T: Exponential stability for abstract linear autonomous functional-differential equations with infinite delay. International Journal of Mathematics and Mathematical Sciences 1998,21(2):255-259. 10.1155/S0161171298000362
Liang J, Xiao TJ: Functional-differential equations with infinite delay in Banach spaces. International Journal of Mathematics and Mathematical Sciences 1991,14(3):497-508. 10.1155/S0161171291000686
Liang J, Xiao T-J: The Cauchy problem for nonlinear abstract functional differential equations with infinite delay. Computers & Mathematics with Applications 2000,40(6-7):693-703. 10.1016/S0898-1221(00)00188-7
Liang J, Xiao T-J: Solvability of the Cauchy problem for infinite delay equations. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):271-297. 10.1016/j.na.2004.05.005
Liang J, Xiao T-J: Solutions to nonautonomous abstract functional equations with infinite delay. Taiwanese Journal of Mathematics 2006,10(1):163-172.
Liang J, Xiao T-J, van Casteren J: A note on semilinear abstract functional differential and integrodifferential equations with infinite delay. Applied Mathematics Letters 2004,17(4):473-477. 10.1016/S0893-9659(04)90092-4
Xiao T-J, Liang J: Blow-up and global existence of solutions to integral equations with infinite delay in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):e1442-e1447. 10.1016/j.na.2009.01.204
Lakshmikantham V, Leela S, Vasundhara J: Theory of Fractional Dynamic Systems. Cambridge Academic, Cambridge, UK; 2009.
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Lakshmikantham V, Vatsala AS: Theory of fractional differential inequalities and applications. Communications in Applied Analysis 2007,11(3-4):395-402.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Agarwal RP, Benchohra M, Slimani BA: Existence results for differential equations with fractional order and impulses. Memoirs on Differential Equations and Mathematical Physics 2008, 44: 1-21.
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: Existence results for fractional order functional differential equations with infinite delay. Journal of Mathematical Analysis and Applications 2008,338(2):1340-1350. 10.1016/j.jmaa.2007.06.021
Anguraj A, Karthikeyan P, N'Guérékata GM: Nonlocal Cauchy problem for some fractional abstract integro-differential equations in Banach spaces. Communications in Mathematical Analysis 2009,6(1):31-35.
Mophou GM, N'Guérékata GM: Mild solutions for semilinear fractional differential equations. Electronic Journal of Differential Equations 2009,2009(21):1-9.
Mophou GM, Nakoulima O, N'Guérékata GM: Existence results for some fractional differential equations with nonlocal conditions. Nonlinear Studies 2010,17(1):15-22.
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
Hale JK, Kato J: Phase space for retarded equations with infinite delay. Funkcialaj Ekvacioj 1978,21(1):11-41.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos, Solitons and Fractals 2002,14(3):433-440. 10.1016/S0960-0779(01)00208-9
El-Borai MM: On some stochastic fractional integro-differential equations. Advances in Dynamical Systems and Applications 2006,1(1):49-57.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mophou, G.M., N'Guérékata, G.M. A Note on a Semilinear Fractional Differential Equation of Neutral Type with Infinite Delay. Adv Differ Equ 2010, 674630 (2010). https://doi.org/10.1155/2010/674630
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/674630
 is in
is in 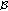 ,
,
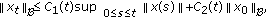
 such that for all
such that for all  ,
, 
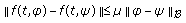
 , with
, with  such that the function
such that the function 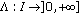 defined by:
defined by: