- Research Article
- Open access
- Published:
A Note on 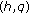 -Genocchi Polynomials and Numbers of Higher Order
-Genocchi Polynomials and Numbers of Higher Order
Advances in Difference Equations volume 2010, Article number: 309480 (2010)
Abstract
We investigate several arithmetic properties of  -Genocchi polynomials and numbers of higher order.
-Genocchi polynomials and numbers of higher order.
1. Introduction and Preliminaries
Recently, Kim [1] studied  -Genocchi and Euler numbers using Fermionic
-Genocchi and Euler numbers using Fermionic  -integral and introduced related applications. Kim [2] also gives the
-integral and introduced related applications. Kim [2] also gives the  -extensions of the Euler numbers which can be viewed as interpolating of
-extensions of the Euler numbers which can be viewed as interpolating of  -analogue of Euler zeta function at negative integers and gives Bernoulli numbers at negative integers by interpolating Riemann zeta function. These numbers are very useful for number theory and mathematical physics. Kim [3, 4] studied
-analogue of Euler zeta function at negative integers and gives Bernoulli numbers at negative integers by interpolating Riemann zeta function. These numbers are very useful for number theory and mathematical physics. Kim [3, 4] studied  -Bernoulli numbers and polynomials related to Gaussian binomial coefficient and studied also some identities of
-Bernoulli numbers and polynomials related to Gaussian binomial coefficient and studied also some identities of  -Euler polynomials and
-Euler polynomials and  -stirling numbers. Kim [5] made Dedekind DC sum in the meaning of extension of Dedekind sum or Hardy sum and introduced lots of interesting results. The purpose of this paper is to investigate several arithmetic properties of
-stirling numbers. Kim [5] made Dedekind DC sum in the meaning of extension of Dedekind sum or Hardy sum and introduced lots of interesting results. The purpose of this paper is to investigate several arithmetic properties of  -Genocchi polynomials and numbers of higher order.
-Genocchi polynomials and numbers of higher order.
Let  be a fixed odd prime. Throughout this paper
be a fixed odd prime. Throughout this paper  ,
,  ,
,  , and
, and  will, respectively, denote the ring of rational integers, the ring of
will, respectively, denote the ring of rational integers, the ring of  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, and the completion of algebraic closure of
-adic rational numbers, and the completion of algebraic closure of  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  When one talks of
When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex number
is variously considered as an indeterminate, a complex number  or a
or a  -adic number
-adic number  . If
. If  one normally assumes
one normally assumes  If
If  then we assume
then we assume  so that
so that  for
for  . We also use the notations
. We also use the notations

for all  (see [5–12]). Hence,
(see [5–12]). Hence,  .
.
Let  be a fixed positive integer with
be a fixed positive integer with  . We now set
. We now set

where  lies in
lies in  . For any
. For any  , we set
, we set

and this can be extended to a distribution on  .
.
We say that  is a uniformly differentiable function at a point
is a uniformly differentiable function at a point  and write
and write  , if the difference quotients
, if the difference quotients  have a limit
have a limit  as
as  (cf. [13–23]).
(cf. [13–23]).
For  , the
, the  -adic invariant integral on
-adic invariant integral on  is defined as
is defined as

(see [14, 23]). Let  and
and  . From (1.4), we have
. From (1.4), we have

The  -adic integral has been used in many areas such as mathematics, physics, probability theory, dynamical systems, and biological models. Especially, Khrennikov [24–26] applied to many areas using ingenious technique. The Genocchi numbers
-adic integral has been used in many areas such as mathematics, physics, probability theory, dynamical systems, and biological models. Especially, Khrennikov [24–26] applied to many areas using ingenious technique. The Genocchi numbers  and polynomials
and polynomials  are defined by the generating functions as follows:
are defined by the generating functions as follows:

(see [5, 7, 15]). The  -extension of Genocchi numbers are defined by
-extension of Genocchi numbers are defined by

(see [1, 2]), and the  -extension of Genocchi polynomials is also given by
-extension of Genocchi polynomials is also given by

In Section 2, we investigate several arithmetic properties of  -Genocchi polynomials and numbers of higher order.
-Genocchi polynomials and numbers of higher order.
2. 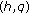 -Genocchi Numbers of Higher Order
-Genocchi Numbers of Higher Order
Let  and
and  with
with  . The
. The  -Genocchi polynomials
-Genocchi polynomials  of order
of order  are defined as
are defined as

where  . It is easily to see that
. It is easily to see that  for each
for each  and
and  . From (2.1), we can obtain the following theorem.
. From (2.1), we can obtain the following theorem.
Theorem 2.1.
Let  and
and  . Then for all
. Then for all  ,
,

From Theorem 2.1, if we take  , then
, then

Now, we define  -Genocchi number of higher order as follows:
-Genocchi number of higher order as follows:

From (2.4), we can derive the following theorem.
Theorem 2.2.
Let  and
and  . Then one has
. Then one has

where  .
.
Note that  , where
, where  are the ordinary Genocchi numbers of order
are the ordinary Genocchi numbers of order  defined as
defined as

By (2.4) and (2.5), we can obtain the following theorem.
Theorem 2.3.
Let  . Then one has
. Then one has

It is easily to check that

where  with
with  . Thus we have the following theorem.
. Thus we have the following theorem.
Theorem 2.4.
Let  with
with  . Then for all
. Then for all  ,
,

We note that if we take  , then we have
, then we have

where  . By (2.10), we easily see that
. By (2.10), we easily see that

Note that  , where
, where  are the
are the  th Genocchi numbers defined as
th Genocchi numbers defined as

From (2.11), we can see that

Let  be the generating function of
be the generating function of  as follows:
as follows:

By (2.7) and (2.14), we see that

By (2.14) and (2.15), we can obtain the following theorem.
Theorem 2.5.
Let  . Then for all
. Then for all  ,
,

References
Kim T:On the multiple
 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055Kim T:Note on the Euler
 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007Kim T:
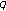 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.Kim T:Some identities on the
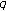 -Euler polynomials of higher order and
-Euler polynomials of higher order and 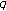 -Stirling numbers by the fermionic
-Stirling numbers by the fermionic 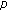 -adic integral on
-adic integral on 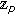 . Russian Journal of Mathematical Physics 2009, 16: 501-508.
. Russian Journal of Mathematical Physics 2009, 16: 501-508.Kim T: Note on Dedekind type DC sums. Advanced Studies in Contemporary Mathematics 2009,18(2):249-260.
Kim T:A note on some formulae for the
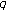 -Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2006,9(2):227-232.
-Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2006,9(2):227-232.Kim T:A note on the generalized
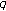 -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):45-50.
-Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):45-50.Kim T:Note on the
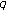 -Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.
-Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.Kim Y-H, Kim W, Ryoo CS:On the twisted
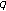 -Euler zeta function associated with twisted
-Euler zeta function associated with twisted 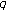 -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):93-100.
-Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):93-100.Ozden H, Simsek Y, Rim S-H, Cangul IN:A note on
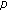 -adic
-adic 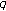 -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.
-Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.Simsek Y: Generating functions of the twisted Bernoulli numbers and polynomials associated with their interpolation functions. Advanced Studies in Contemporary Mathematics 2008,16(2):251-278.
Simsek Y, Kurt V, Kim D:New approach to the complete sum of products of the twisted
 -Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44-56. 10.2991/jnmp.2007.14.1.5
-Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44-56. 10.2991/jnmp.2007.14.1.5Cenkci M, Simsek Y, Kurt V:Further remarks on multiple
 -adic
-adic  -
- -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.Kim T:
 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.Kim T: On Euler-Barnes multiple zeta functions. Russian Journal of Mathematical Physics 2003,10(3):261-267.
Kim T:Analytic continuation of multiple
 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.Kim T:Power series and asymptotic series associated with the
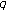 -analog of the two-variable
-analog of the two-variable  -adic
-adic 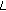 -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.Kim T:Multiple
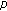 -adic
-adic 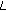 -function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038Kim T:A note on
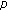 -adic
-adic  -integral on
-integral on 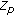 associated with
associated with 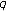 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.Kim T:On
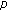 -adic interpolating function for
-adic interpolating function for 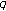 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027Kim T:On the analogs of Euler numbers and polynomials associated with
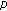 -adic
-adic  -integral on
-integral on 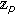 at
at  . Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027Kim T:A note on
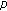 -adic
-adic  -integral on
-integral on 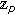 associated with
associated with  -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.Kim T:
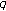 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3Khrennikov AYu: p-adic Valued Distributions and Their Applications to the Mathematical Physics. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1994.
Khrennikov AYu: Non-Archimedean Analysis: Quantum Paradoxes, Dynamical Systems and Biological Models, Mathematics and Its Applications. Volume 427. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:xviii+371.
Khrennikov AYu: Interpretations of Probability. VSP, Utrecht, The Netherlands; 1999:ii+228.
Acknowledgment
This paper was supported by KOSEF (2009-0073396, 2009-A419-0065).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jang, LC., Hwang, KW. & Kim, YH. A Note on 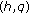 -Genocchi Polynomials and Numbers of Higher Order.
Adv Differ Equ 2010, 309480 (2010). https://doi.org/10.1155/2010/309480
-Genocchi Polynomials and Numbers of Higher Order.
Adv Differ Equ 2010, 309480 (2010). https://doi.org/10.1155/2010/309480
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/309480
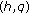 -Genocchi Numbers of Higher Order
-Genocchi Numbers of Higher Order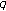 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481-486. 10.1134/S1061920808040055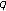 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007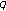 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.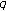 -Euler polynomials of higher order and
-Euler polynomials of higher order and 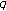 -Stirling numbers by the fermionic
-Stirling numbers by the fermionic 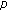 -adic integral on
-adic integral on 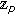 . Russian Journal of Mathematical Physics 2009, 16: 501-508.
. Russian Journal of Mathematical Physics 2009, 16: 501-508.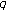 -Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2006,9(2):227-232.
-Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2006,9(2):227-232.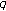 -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):45-50.
-Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):45-50.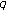 -Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.
-Euler numbers of higher order. Advanced Studies in Contemporary Mathematics 2009,19(1):25-29.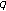 -Euler zeta function associated with twisted
-Euler zeta function associated with twisted 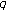 -Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):93-100.
-Euler numbers. Proceedings of the Jangjeon Mathematical Society 2009,12(1):93-100.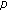 -adic
-adic 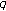 -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.
-Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14: 233-239.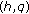 -Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44-56. 10.2991/jnmp.2007.14.1.5
-Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44-56. 10.2991/jnmp.2007.14.1.5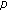 -adic
-adic  -
- -function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.
-function of two variables. Advanced Studies in Contemporary Mathematics 2007,14(1):49-68.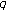 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.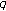 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.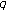 -analog of the two-variable
-analog of the two-variable  -adic
-adic 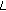 -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.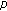 -adic
-adic 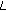 -function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038
-function. Russian Journal of Mathematical Physics 2006,13(2):151-157. 10.1134/S1061920806020038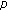 -adic
-adic  -integral on
-integral on 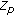 associated with
associated with 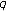 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007, 15: 133-138.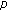 -adic interpolating function for
-adic interpolating function for 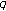 -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027
-Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008,339(1):598-608. 10.1016/j.jmaa.2007.07.027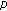 -adic
-adic  -integral on
-integral on 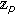 at
at  . Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027
. Journal of Mathematical Analysis and Applications 2007,331(2):779-792. 10.1016/j.jmaa.2006.09.027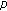 -adic
-adic  -integral on
-integral on 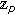 associated with
associated with  -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133-137.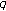 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15-27. 10.2991/jnmp.2007.14.1.3