- Research Article
- Open access
- Published:
Uniform Attractor for the Partly Dissipative Nonautonomous Lattice Systems
Advances in Difference Equations volume 2009, Article number: 916316 (2009)
Abstract
The existence of uniform attractor in  is proved for the partly dissipative nonautonomous lattice systems with a new class of external terms belonging to
is proved for the partly dissipative nonautonomous lattice systems with a new class of external terms belonging to  , which are locally asymptotic smallness and translation bounded but not translation compact in
, which are locally asymptotic smallness and translation bounded but not translation compact in  . It is also showed that the family of processes corresponding to nonautonomous lattice systems with external terms belonging to weak topological space possesses uniform attractor, which is identified with the original one. The upper semicontinuity of uniform attractor is also studied.
. It is also showed that the family of processes corresponding to nonautonomous lattice systems with external terms belonging to weak topological space possesses uniform attractor, which is identified with the original one. The upper semicontinuity of uniform attractor is also studied.
1. Introduction
This paper is concerned with the long-time behavior of the following non-autonomous lattice systems:


with initial conditions

where  is the integer lattice;
is the integer lattice;  is a nonlinear function satisfying
is a nonlinear function satisfying  ;
;  is a positive self-adjoint linear operator;
is a positive self-adjoint linear operator;  belong to certain metric space, which will be given in the following.
belong to certain metric space, which will be given in the following.
Lattice dynamical systems occur in a wide variety of applications, where the spatial structure has a discrete character, for example, chemical reaction theory, electrical engineering, material science, laser, cellular neural networks with applications to image processing and pattern recognition; see [1–4]. Thus, a great interest in the study of infinite lattice systems has been raising. Lattice differential equations can be considered as a spatial or temporal discrete analogue of corresponding partial differential equations on unbounded domains. It is well known that the long-time behavior of solutions of partial differential equations on unbounded domains raises some difficulty, such as well-posedness and lack of compactness of Sobolev embeddings for obtaining existence of global attractors. Authors in [5–7] consider the autonomous partial equations on unbounded domain in weighted spaces, using the decaying of weights at infinity to get the compactness of solution semigroup. In [8–10], asymptotic compactness of the solutions is used to obtain existence of global compact attractors for autonomous system on unbounded domain. Authors in [11] consider them in locally uniform space. For non-autonomous partial differential equations on bounded domain, many studies on the existence of uniform attractor have been done, for example [12–14].
For lattice dynamical systems, standard theory of ordinary differential equations can be applied to get the well-posedness of it. "Tail ends" estimate method is usually used to get asymptotic compactness of autonomous infinite-dimensional lattice, and by this the existence of global compact attractor is obtained; see [15–17]. Authors in [18, 19] also prove that the uniform smallness of solutions of autonomous infinite lattice systems for large space and time variables is sufficient and necessary conditions for asymptotic compactness of it. Recently, "tail ends" method is extended to non-autonomous infinite lattice systems; see [20–22]. The traveling wave solutions of lattice differential equations are studied in [23–25]. In [18, 26, 27], the existence of global attractors of autonomous infinite lattice systems is obtained in weighted spaces, which do not exclude traveling wave.
In this paper, we investigate the existence of uniform attractor for non-autonomous lattice systems (1.1)–(1.3). The external term in [20] is supposed to belong to  and to be almost periodic function. By Bochner-Amerio criterion, the set of this external term's translation is precompact in
and to be almost periodic function. By Bochner-Amerio criterion, the set of this external term's translation is precompact in  . Based on ideas of [28], authors in [14] introduce uniformly
. Based on ideas of [28], authors in [14] introduce uniformly  -limit compactness, and prove that the family of weakly continuous processes with respect to (w.r.t.) certain symbol space possesses compact uniform attractors if the process has a bounded uniform absorbing set and is uniformly
-limit compactness, and prove that the family of weakly continuous processes with respect to (w.r.t.) certain symbol space possesses compact uniform attractors if the process has a bounded uniform absorbing set and is uniformly  -limit compact. Motivated by this, we will prove that the process corresponding to problem (1.1)–(1.3) with external terms being locally asymptotic smallness (see Definition 4.5) possesses a compact uniform attractor in
-limit compact. Motivated by this, we will prove that the process corresponding to problem (1.1)–(1.3) with external terms being locally asymptotic smallness (see Definition 4.5) possesses a compact uniform attractor in  , which coincides with uniform attractor of the family of processes with external terms belonging to weak closure of translation set of locally asymptotic smallness function in
, which coincides with uniform attractor of the family of processes with external terms belonging to weak closure of translation set of locally asymptotic smallness function in  . We also show that locally asymptotic functions are translation bounded in
. We also show that locally asymptotic functions are translation bounded in  , but not translation compact (tr.c.) in
, but not translation compact (tr.c.) in  . Since the locally asymptotic smallness functions are not necessary to be translation compact in
. Since the locally asymptotic smallness functions are not necessary to be translation compact in  , compared with [20], the conditions on external terms of (1.1)–(1.3) can be relaxed in this paper.
, compared with [20], the conditions on external terms of (1.1)–(1.3) can be relaxed in this paper.
This paper is organized as follows. In Section 2, we give some preliminaries and present our main result. In Section 3, the existence of a family of processes for (1.1)–(1.3) is obtained. We also show that the family of processes possesses a uniformly (w.r.t  ) absorbing set. In Section 4, we prove the existence of uniform attractor. In Section 5, the upper semicontinuity of uniform attractor will be studied.
) absorbing set. In Section 4, we prove the existence of uniform attractor. In Section 5, the upper semicontinuity of uniform attractor will be studied.
2. Main Result
In this section, we describe our main result. Denote by  the Hilbert space defined by
the Hilbert space defined by

with the inner product  and norm
and norm  given by
given by

For  , we endow with the inner and norm as. For
, we endow with the inner and norm as. For 

Denote by  the space of function
the space of function  with values in
with values in  that locally 2-power integrable in the Bochner sense, that is,
that locally 2-power integrable in the Bochner sense, that is,

It is equipped with the local 2-power mean convergence topology. Then,  is a metrizable space. Let
is a metrizable space. Let  be a space of functions
be a space of functions  from
from  such that
such that

Denote by  the space
the space  endow with the local weak convergence topology.
endow with the local weak convergence topology.
For each sequence  define linear operators on
define linear operators on  by
by

Then

For convenience, initial value problem (1.1)–(1.3) can be written as


with initial conditions

where  ,
,  .
.
In the following, we give some assumption on nonlinear function  , and
, and  :
:

There exists a positive-value continuous function  such that
such that

There exist positive constants  such that
such that

Let the external term  belong to
belong to  , it follows from the standard theory of ordinary differential equations that there exists a unique local solution
, it follows from the standard theory of ordinary differential equations that there exists a unique local solution  for problem (2.8)–(2.10) if (H
1
)–(H
3
) hold. For a fixed external term
for problem (2.8)–(2.10) if (H
1
)–(H
3
) hold. For a fixed external term  , take the symbol space
, take the symbol space  , the set contains all translations of
, the set contains all translations of  in
in  . Take the
. Take the  the closure of
the closure of  in
in  . Denote by
. Denote by  the translation semigroup,
the translation semigroup,  for all
for all  or
or  ,
,  ,
,  . It is evident that
. It is evident that  is continuous on
is continuous on  in the topology of
in the topology of  and on
and on  in the topology of
in the topology of  , respectively,
, respectively,

In Section 3, we will show that for every  and
and  ,
,  , problem (2.8)–(2.10) has a unique global solution
, problem (2.8)–(2.10) has a unique global solution  Thus, there exists a family of processes
Thus, there exists a family of processes  from
from  to
to  . In order to obtain the uniform attractor of the family of processes, we suppose the external term is locally asymptotic smallness (see Definition 4.5). Let
. In order to obtain the uniform attractor of the family of processes, we suppose the external term is locally asymptotic smallness (see Definition 4.5). Let  be a Banach space which the processes acting in, for a given symbol space
be a Banach space which the processes acting in, for a given symbol space  , the uniform (w.r.t.
, the uniform (w.r.t.  )
)  -limit set
-limit set  of
of  is defined by
is defined by

The first result of this paper is stated in the following, which will be proved in Section 4.
Theorem 2 A.
Assume that  be locally asymptotic smallness and
be locally asymptotic smallness and  hold. Then the process
hold. Then the process  corresponding to problems (2.8)–(2.10) with external term
corresponding to problems (2.8)–(2.10) with external term  possesses compact uniform
possesses compact uniform  attractor
attractor  in
in  which coincides with uniform (w.r.t.
which coincides with uniform (w.r.t.  attractor
attractor  for the family of processes
for the family of processes  ,
,  , that is,
, that is,

where  is the uniform
is the uniform  absorbing set in
absorbing set in  , and
, and  is kernel of the process
is kernel of the process  . The uniform attractor uniformly
. The uniform attractor uniformly  attracts the bounded set in
attracts the bounded set in  .
.
We also consider finite-dimensional approximation to the infinite-dimensional systems (1.2)-(1.3) on finite lattices. For every positive integer  , let
, let  , consider the following ordinary equations with initial data in
, consider the following ordinary equations with initial data in  :
:

In Section 5, we will show that the finite-dimensional approximation systems possess a uniform attractor  in
in  , and these uniform attractors are upper semicontinuous when
, and these uniform attractors are upper semicontinuous when  . More precisely, we have the following theorem.
. More precisely, we have the following theorem.
Theorem 2 B.
Assume that  and
and  hold. Then for every positive integer
hold. Then for every positive integer  , systems (2.17) possess compact uniform attractor
, systems (2.17) possess compact uniform attractor  . Further,
. Further,  is upper semicontinuous to
is upper semicontinuous to  as
as  , that is,
, that is,

where

3. Processes and Uniform Absorbing Set
In this section, we show that the process can be defined and there exists a bounded uniform absorbing set for the family of processes.
Lemma 3.1.
Assume that  and
and  hold. Let
hold. Let  , and
, and  . Then the solution of (2.8)–(2.10) satisfies
. Then the solution of (2.8)–(2.10) satisfies

where  ,
,  .
.
Proof.
Taking the inner product of (2.8) with  in
in  , by
, by  we get
we get

Similarly, taking the inner product of (2.9) with  in
in  , we get
, we get

Note that

Summing up (3.2) and (3.3), from (3.4), we get

Thus, by  ,
,

Since  , from [12, Proposition V.4.2.], we have
, from [12, Proposition V.4.2.], we have

From (3.6)-(3.7), applying Gronwall's inequality of generalization (see [12, Lemma II.1.3]), we get (3.1). The proof is completed.
It follows from Lemma 3.1 that the solution  of problem (2.8)–(2.10) is defined for all
of problem (2.8)–(2.10) is defined for all  . Therefore, there exists a family processes acting in the space
. Therefore, there exists a family processes acting in the space  ,
,  ,
,  ,
,  , where
, where  is the solution of (2.8)–(2.10), and the time symbol
is the solution of (2.8)–(2.10), and the time symbol  belongs to
belongs to  and
and  , respectively. The family of processes
, respectively. The family of processes  satisfies multiplicative properties:
satisfies multiplicative properties:

Furthermore, the following translation identity holds:

The kernel  of the processes
of the processes  consists of all bounded complete trajectories of the process
consists of all bounded complete trajectories of the process  , that is,
, that is,

 denotes the kernel section at a times moment
denotes the kernel section at a times moment  :
:

Lemma 3.1 also shows that the family of processes possesses a uniform absorbing set in  .
.
Lemma 3.2.
Assume that  and
and  hold. Let
hold. Let  . Then, there exists a bounded uniform absorbing set
. Then, there exists a bounded uniform absorbing set  in
in  for the family of processes
for the family of processes  , that is, for any bounded set
, that is, for any bounded set  , there exists
, there exists  ,
,

Proof.
Let  , from (3.1) we have
, from (3.1) we have

where

Let  . The proof is completed.
. The proof is completed.
4. Uniform Attractor
In this section, we establish the existence of uniform attractor for the non-autonomous lattice systems (2.8)–(2.10). Let  be a Banach space, and let
be a Banach space, and let  be a subset of some Banach space.
be a subset of some Banach space.
Definition 4.1.
 is said to be
is said to be  weakly continuous, if for any
weakly continuous, if for any  , the mapping
, the mapping  is weakly continuous from
is weakly continuous from  to
to  .
.
A family of processes  ,
,  is said to be uniformly
is said to be uniformly -limit compact if for any
-limit compact if for any  and bounded set
and bounded set  , the set
, the set  is bounded for every
is bounded for every  and
and  is precompact set as
is precompact set as  . We need the following result in [14].
. We need the following result in [14].
Theorem 4.2.
Let  be the weak closure of
be the weak closure of  . Assume that
. Assume that  ,
,  is
is  weakly continuous, and
weakly continuous, and
-
(i)
has a bounded uniformly (w.r.t.
 ) absorbing set
) absorbing set 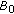 ,
, -
(ii)
is uniformly (w.r.t.
 )
)  -limit compact.
-limit compact.
Then the families of processes  ,
,  ,
,  possess, respectively, compact uniform (w.r.t.
possess, respectively, compact uniform (w.r.t.  ,
,  , resp.) attractors
, resp.) attractors  and
and  satisfying
satisfying

Furthermore,  is nonempty for all
is nonempty for all  .
.
Let  be a Banach space and
be a Banach space and  , denote the space
, denote the space  of functions
of functions  ,
,  with values in
with values in  that are locally
that are locally  -power integral in the Bochner sense, it is equipped with the local
-power integral in the Bochner sense, it is equipped with the local  -power mean convergence topology. Recall the Propositions in [12].
-power mean convergence topology. Recall the Propositions in [12].
Proposition 4.3.
A set  is precompact in
is precompact in  if and only if the set
if and only if the set  is precompact in
is precompact in  for every segment
for every segment  . Here,
. Here,  denotes the restriction of the set
denotes the restriction of the set  to the segment
to the segment  .
.
Proposition 4.4.
A function  is tr.c. in
is tr.c. in  if and only if
if and only if
-
(i)
for any
 the set
the set 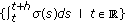 is precompact in
is precompact in  ;
; -
(ii)
there exists a function
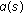 ,
, 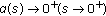 such that
such that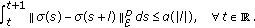 (42)
(42)
Now, one introduces a class of function.
Definition 4.5.
A function  is said to be locally asymptotic smallness if for any
is said to be locally asymptotic smallness if for any  , there exists positive integer
, there exists positive integer  such that
such that

Denote by  the set of all locally asymptotic smallness functions in
the set of all locally asymptotic smallness functions in  . It is easy to see that
. It is easy to see that  . The next examples show that there exist functions in
. The next examples show that there exist functions in  but not in
but not in  , and a function belongs to
, and a function belongs to  is not necessary a tr.c. function in
is not necessary a tr.c. function in  .
.
Example 4.6.
Let  ,
,

For every  ,
,  ,
,

Thus,

and  . However, for every positive integer
. However, for every positive integer  , and for any positive
, and for any positive  ,
,

Therefore,  .
.
Example 4.7.
 ,
,

for  ,
,

Here,  denote the positive integer set.
denote the positive integer set.
For every positive integer  ,
,  , and for
, and for  ,
,

which implies that

Therefore,  . Note that for any
. Note that for any  ,
,

From Proposition 4.4,  is not translation compact in
is not translation compact in  .
.
Remark 4.8.
Example 4.7 shows that a locally asymptotic function is not necessary translation compact in  .
.
In the following, we give some properties of locally asymptotic smallness function.
Lemma 4.9.
 is a closed subspace of
is a closed subspace of  .
.
Proof.
Let  such that
such that

Then, for any  , there exists positive integer
, there exists positive integer  such that for every
such that for every  ,
,

Since  , there exist
, there exist  such that for all
such that for all  ,
,

Let  , we get that
, we get that

Therefore,  . This completes the proof.
. This completes the proof.
Lemma 4.10.
Every translation compact function  in
in  is locally asymptotic smallness.
is locally asymptotic smallness.
Proof.
Since  is tr.c. in
is tr.c. in  , we get that
, we get that  is precompact in
is precompact in  . By Proposition 4.3, we get that
. By Proposition 4.3, we get that  is precompact in
is precompact in  . Thus, for any
. Thus, for any  , there exists finite number
, there exists finite number  such that for every
such that for every  , there exist some
, there exist some  ,
,  , such that
, such that

For the  given above,
given above,  implies that there exists positive integer
implies that there exists positive integer  such that
such that

Therefore,

which implies  is locally asymptotic smallness. This completes the proof.
is locally asymptotic smallness. This completes the proof.
We now establish the uniform estimates on the tails of solutions of (2.8)–(2.10) as  .
.
Lemma 4.11.
Assume that  hold and
hold and  is locally asymptotic smallness. Then for any
is locally asymptotic smallness. Then for any  , there exist positive integer
, there exist positive integer  and
and  such that if
such that if  ,
,  ,
,  satisfies
satisfies

Proof.
Choose a smooth function  such that
such that  for
for  , and
, and

and there exists a constant  such that
such that  for
for  . Let
. Let  be a suitable large positive integer,
be a suitable large positive integer,  . Taking the inner product of (2.8) with
. Taking the inner product of (2.8) with  and (2.9) with
and (2.9) with  in
in  , we have
, we have

From  , we have
, we have

where  is same as in Lemma 3.1
is same as in Lemma 3.1

 as in (3.10)
as in (3.10)

Summing up (4.22), from (4.23)–(4.25) we get

Thus,

We now estimate the integral term on the right-hand side of (4.27).

Similarly,

Since  is locally asymptotic smallness, from (4.27)–(4.29) we get that for any
is locally asymptotic smallness, from (4.27)–(4.29) we get that for any  , if
, if  , there exist
, there exist  and sufficient large positive integer
and sufficient large positive integer  such that
such that

The proof is completed.
Lemma 4.12.
Assume that  hold, let
hold, let  ,
,  . If
. If  in
in  and
and  weakly in
weakly in  , then for any
, then for any  ,
,

Proof.
Let  ,
,  . Since
. Since  is bounded in
is bounded in  , by Lemma 3.2, we get that
, by Lemma 3.2, we get that

Therefore, for all  ,
,  ,
,

Note that  is the solution of (2.8) and (2.9) with time symbol
is the solution of (2.8) and (2.9) with time symbol  , it follow from (4.32) that
, it follow from (4.32) that

In the following, we show that  . By the fact that
. By the fact that  is the solution of (2.8) and (2.9), for any
is the solution of (2.8) and (2.9), for any  , we get that
, we get that

Note that  weakly in
weakly in  . Let
. Let  in (4.35), by (4.34) we get that
in (4.35), by (4.34) we get that  is the solution of (2.8) and (2.9) with the initial data
is the solution of (2.8) and (2.9) with the initial data  . By the unique solvability of problem (2.8)–(2.10), we get that
. By the unique solvability of problem (2.8)–(2.10), we get that  . This completes the proof.
. This completes the proof.
Proof of Theorem A.
From Lemmas 3.2, 4.11 and 4.12, and Theorem 4.2, we get the results.
5. Upper Semicontinuity of Attractors
In this section, we present the approximation to the uniform attractor  obtained in Theory A by the uniform attractor of following finite-dimensional lattice systems in
obtained in Theory A by the uniform attractor of following finite-dimensional lattice systems in  :
:

with the initial data

and the periodic boundary conditions

Similar to systems (2.8)–(2.10), under the assumption  , the approximation systems (5.1)–(5.2) with
, the approximation systems (5.1)–(5.2) with  possess a unique solution
possess a unique solution  , which continuously depends on initial data. Therefore, we can associate a family of processes
, which continuously depends on initial data. Therefore, we can associate a family of processes  which satisfy similar properties (3.8)–(3.9). Similar to Lemma 3.2, we have the following result.
which satisfy similar properties (3.8)–(3.9). Similar to Lemma 3.2, we have the following result.
Lemma 5.1.
Assume that  , and
, and  hold. Let
hold. Let  . Then, there exists a bounded uniform absorbing set
. Then, there exists a bounded uniform absorbing set  for the family of processes
for the family of processes  , that is, for any bounded set
, that is, for any bounded set  , there exists
, there exists  , for
, for  ,
,

In particular,  is independent of
is independent of  and
and  .
.
Since (5.1) is finite-dimensional systems, it is easy to know that under the assumption of Lemma 5.1, the family of processes  ,
,  is uniformly (w.r.t.
is uniformly (w.r.t.  )
)  -limit compact. Similar to Lemma 4.12, if
-limit compact. Similar to Lemma 4.12, if  in
in  ,
,  weakly in
weakly in  , then for any
, then for any  ,
,  ,
,

Lemma 5.2.
Assume that  and
and  hold. Then the process
hold. Then the process  corresponding to problems (5.1)-(5.2) with external term
corresponding to problems (5.1)-(5.2) with external term  possesses compact uniform (w.r.t.
possesses compact uniform (w.r.t.  ) attractor
) attractor  in
in  which coincides with uniform (w.r.t.
which coincides with uniform (w.r.t.  attractor
attractor  for the family of processes
for the family of processes  ,
,  , that is,
, that is,

where  is the uniform
is the uniform  absorbing set in
absorbing set in  , and
, and  is kernel of the process
is kernel of the process  . The uniform attractor uniformly
. The uniform attractor uniformly  attracts the bounded set in
attracts the bounded set in  .
.
Proof of Theorem B.
If  , it follows from Lemma 5.2 that there exist
, it follows from Lemma 5.2 that there exist  and a bounded complete solution
and a bounded complete solution  such that
such that

Since  , there exist
, there exist  and a subsequence of
and a subsequence of  , which is still denote by
, which is still denote by  , such that
, such that

From Lemma 5.1, we get that

which imply that

Thus,

Let  be a sequence of compact intervals of
be a sequence of compact intervals of  such that
such that  and
and  . From (5.9) and (5.11), using Ascoli's theorem, we get that for each
. From (5.9) and (5.11), using Ascoli's theorem, we get that for each  , there exists a subsequence of
, there exists a subsequence of  (still denoted by
(still denoted by  ) and
) and  such that
such that

Proceeding as in the proof of Lemma 4.11, we get that the weak convergence is actually strong convergence, and therefore  is precompact in
is precompact in  for each
for each  . Then we infer that there exists a subsequence
. Then we infer that there exists a subsequence  of
of  and
and  such that
such that  converges to
converges to  . Using Ascoli's theorem again, we get, by induction, that there is a subsequence
. Using Ascoli's theorem again, we get, by induction, that there is a subsequence  of
of  such that
such that  converges to
converges to  in
in  , where
, where  is an extension of
is an extension of  to
to  . Finally, taking a diagonal subsequence in the usual way, we find that there exist a subsequence
. Finally, taking a diagonal subsequence in the usual way, we find that there exist a subsequence  of
of  and
and  such that for any compact interval
such that for any compact interval 

From (5.9) we get that

Next, we show that  is the solution of (2.8)–(2.10). It follows from (5.10) that
is the solution of (2.8)–(2.10). It follows from (5.10) that

For fixed  , let
, let  . Since
. Since  is the solution of (5.1)–(5.2) with
is the solution of (5.1)–(5.2) with  , we have
, we have

Thus, for each  , we have
, we have

Letting  , by (5.8), (5.13), (5.15) and (5.17) we find that
, by (5.8), (5.13), (5.15) and (5.17) we find that  satisfies
satisfies

Since  is arbitrary, we note that (5.18) are valid for all
is arbitrary, we note that (5.18) are valid for all  . From (5.14) we find that
. From (5.14) we find that  is a bounded complete solution of (2.8)–(2.10). Therefore,
is a bounded complete solution of (2.8)–(2.10). Therefore,  . By (5.13) we get that
. By (5.13) we get that

The proof is complete.
Remark 5.3.
All the result of this paper is valid for the systems in [20, 21].
References
Arima T, Fukuyo K, Idemitsu K, Inagaki Y: Molecular dynamic simulations of yttri-astabilized zirconia between 300 and 200 K. Journal of Molecular Liquids 2004, 113: 67-73. 10.1016/j.molliq.2004.02.038
Callan JP, Kim AM-T, Huang L, Mazur E: Ultrafast electron and lattice dynamics in semiconductors at high excited carrier densities. Chemical Physics 2000, 251: 167-179. 10.1016/S0301-0104(99)00301-8
Chow S-N, Mallet-Paret J, Van Vleck ES: Pattern formation and spatial chaos in spatially discrete evolution equations. Random & Computational Dynamics 1996,4(2-3):109-178.
Chua LO, Yang L: Cellular neural networks: theory. IEEE Transactions on Circuits and Systems 1988,35(10):1257-1272. 10.1109/31.7600
Babin AV, Vishik MI: Attractors of partial differential evolution equations in an unbounded domain. Proceedings of the Royal Society of Edinburgh. Section A 1990,116(3-4):221-243. 10.1017/S0308210500031498
Efendiev MA, Zelik SV: The attractor for a nonlinear reaction-diffusion system in an unbounded domain. Communications on Pure and Applied Mathematics 2001,54(6):625-688. 10.1002/cpa.1011
Zelik SV: Attractors of reaction-diffusion systems in unbounded domains and their spatial complexity. Communications on Pure and Applied Mathematics 2003,56(5):584-637. 10.1002/cpa.10068
Rodriguez-Bernal A, Wang B:Attractors for partly dissipative reaction diffusion systems in
 . Journal of Mathematical Analysis and Applications 2000,252(2):790-803. 10.1006/jmaa.2000.7122
. Journal of Mathematical Analysis and Applications 2000,252(2):790-803. 10.1006/jmaa.2000.7122Temam R: Infinite-Dimensional Dynamical Systems in Mechanics and Physics, Applied Mathematical Sciences. Volume 68. Springer, New York, NY, USA; 1988:xvi+500.
Wang B: Attractors for reaction-diffusion equations in unbounded domains. Physica D 1999,128(1):41-52. 10.1016/S0167-2789(98)00304-2
Carvalho AN, Dlotko T: Partially dissipative systems in locally uniform space. Cadernos De Matematica 2001, 02: 291-307.
Chepyzhov VV, Vishik MI: Attractors for Equations of Mathematical Physics, American Mathematical Society Colloquium Publications. Volume 49. American Mathematical Society, Providence, RI, USA; 2002:xii+363.
Chepyzhov VV, Vishik MI: Attractors of non-autonomous dynamical systems and their dimension. Journal de Mathématiques Pures et Appliquées 1994, 73: 279-333.
Lu S, Wu H, Zhong C: Attractors for nonautonomous 2D Navier-Stokes equations with normal external forces. Discrete and Continuous Dynamical Systems. Series A 2005,13(3):701-719.
Bates PW, Lu K, Wang B: Attractors for lattice dynamical systems. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering 2001,11(1):143-153. 10.1142/S0218127401002031
Li X-J, Zhong C:Attractors for partly dissipative lattice dynamic systems in
 . Journal of Computational and Applied Mathematics 2005,177(1):159-174. 10.1016/j.cam.2004.09.014
. Journal of Computational and Applied Mathematics 2005,177(1):159-174. 10.1016/j.cam.2004.09.014Zhou S: Attractors for second order lattice dynamical systems. Journal of Differential Equations 2002,179(2):605-624. 10.1006/jdeq.2001.4032
Wang B: Dynamics of systems on infinite lattices. Journal of Differential Equations 2006,221(1):224-245. 10.1016/j.jde.2005.01.003
Zhou S, Shi W: Attractors and dimension of dissipative lattice systems. Journal of Differential Equations 2006,224(1):172-204. 10.1016/j.jde.2005.06.024
Wang B: Asymptotic behavior of non-autonomous lattice systems. Journal of Mathematical Analysis and Applications 2007,331(1):121-136. 10.1016/j.jmaa.2006.08.070
Zhao C, Zhou S: Compact kernel sections of long-wave–short-wave resonance equations on infinite lattices. Nonlinear Analysis: Theory, Methods & Applications 2008,68(3):652-670. 10.1016/j.na.2006.11.027
Zhou S, Zhao C, Liao X: Compact uniform attractors for dissipative non-autonomous lattice dynamical systems. Communications on Pure and Applied Analysis 2007,6(4):1087-1111.
Bates PW, Chen X, Chmaj AJJ: Traveling waves of bistable dynamics on a lattice. SIAM Journal on Mathematical Analysis 2003,35(2):520-546. 10.1137/S0036141000374002
Chow S-N, Mallet-Paret J, Shen W: Traveling waves in lattice dynamical systems. Journal of Differential Equations 1998,149(2):248-291. 10.1006/jdeq.1998.3478
Zinner B: Existence of traveling wavefront solutions for the discrete Nagumo equation. Journal of Differential Equations 1992,96(1):1-27. 10.1016/0022-0396(92)90142-A
Beyn W-J, Pilyugin SY: Attractors of reaction diffusion systems on infinite lattices. Journal of Dynamics and Differential Equations 2003,15(2-3):485-515.
Li X-J, Wang D: Attractors for partly dissipative lattice dynamic systems in weighted spaces. Journal of Mathematical Analysis and Applications 2007,325(1):141-156. 10.1016/j.jmaa.2006.01.054
Ma Q, Wang S, Zhong C: Necessary and sufficient conditions for the existence of global attractors for semigroups and applications. Indiana University Mathematics Journal 2002,51(6):1541-1559. 10.1512/iumj.2002.51.2255
Acknowledgments
The authors are extremely grateful to the anonymous reviewers for their suggestion, and with their help, the version has been improved. This research was supported by the NNSF of China Grant no. 10871059
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, X., Lv, H. Uniform Attractor for the Partly Dissipative Nonautonomous Lattice Systems. Adv Differ Equ 2009, 916316 (2009). https://doi.org/10.1155/2009/916316
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/916316
 ) absorbing set
) absorbing set 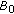 ,
, )
)  -limit compact.
-limit compact. the set
the set 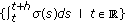 is precompact in
is precompact in  ;
;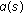 ,
, 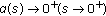 such that
such that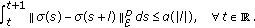
 . Journal of Mathematical Analysis and Applications 2000,252(2):790-803. 10.1006/jmaa.2000.7122
. Journal of Mathematical Analysis and Applications 2000,252(2):790-803. 10.1006/jmaa.2000.7122 . Journal of Computational and Applied Mathematics 2005,177(1):159-174. 10.1016/j.cam.2004.09.014
. Journal of Computational and Applied Mathematics 2005,177(1):159-174. 10.1016/j.cam.2004.09.014