- Research
- Open access
- Published:
Fixed point theory in the setting of \((\alpha,\beta,\psi,\phi)\)-interpolative contractions
Advances in Difference Equations volume 2021, Article number: 339 (2021)
Abstract
In this manuscript we introduce the notion of \((\alpha,\beta,\psi,\phi)\)-interpolative contraction that unifies and generalizes significant concepts: Proinov type contractions, interpolative contractions, and ample spectrum contraction. We investigate the necessary and sufficient conditions to guarantee existence and uniqueness of the fixed point of such mappings.
1 Introduction
For many years researchers in the field of fixed point theory have known and employed contractivity conditions of the type:

where  is a metric space,
is a metric space,  is a self-mapping, and \(\psi ,\phi : [ 0,+ \infty ) \rightarrow [ 0,+ \infty ) \) are two auxiliary functions satisfying certain general conditions whose main aim is to help in the task of proving existence and, in most of cases, uniqueness of fixed points of the mapping
is a self-mapping, and \(\psi ,\phi : [ 0,+ \infty ) \rightarrow [ 0,+ \infty ) \) are two auxiliary functions satisfying certain general conditions whose main aim is to help in the task of proving existence and, in most of cases, uniqueness of fixed points of the mapping  (Boyd and Wong [1], Geraghty [2], Amini-Harandi and Petruşel [3], Jleli and Samet [4], Wardowski [5], etc.) This is only a simple, but interesting, way to generalize the original Banach’s contractivity condition that firstly appeared in [6]. After that, many other ways to generate the Banach contractive mapping principle have appeared [6], based mainly on three distinct directions: on the abstract metric structure of the underlying space, on the formulation of novel increasingly general contractive conditions, and also on the introduction of algebraic (no necessarily metric) structures (binary relations, partial orders [7], fuzzy metrics [8, 9], etc.)
(Boyd and Wong [1], Geraghty [2], Amini-Harandi and Petruşel [3], Jleli and Samet [4], Wardowski [5], etc.) This is only a simple, but interesting, way to generalize the original Banach’s contractivity condition that firstly appeared in [6]. After that, many other ways to generate the Banach contractive mapping principle have appeared [6], based mainly on three distinct directions: on the abstract metric structure of the underlying space, on the formulation of novel increasingly general contractive conditions, and also on the introduction of algebraic (no necessarily metric) structures (binary relations, partial orders [7], fuzzy metrics [8, 9], etc.)
In the line of research regarding the generalization of contractive conditions, it is worth highlighting the evolution of two distinct models. On the one hand, there are models that are only based on the usage of two main terms: the distance between any two points in space and the distance between their respective images. Along this line, it is worth highlighting the efforts due to Boyd and Wong [1], etc. More recently, Khojasteh et al. [10] introduced the notion of simulation function, which was later subtly modified by Roldán López de Hierro et al. in [11]. After a series of successive research papers deepening this area (see [12–14]), this last author and Shahzad presented the notion of ample spectrum contraction in [15] with a double aim: to analyze the essential properties, from an abstract point of view, that any contraction that may arise in the future must satisfy and generalize as many results as possible in the field of fixed point theory.
On the other hand, the efforts made in the line of research making new terms intervene in the contractive condition (for example, the distance between any point and its image) are also noteworthy. In this line we can highlight the results given by Ćirić, Kannan [16, 17], Hardy-Rogers [18], etc. Inspired by Kannan contractions and the notion of interpolation triple of type γ described in [19], Karapınar introduced in [20] the interpolative Kannan type contractions. Such advance was later extended in [21] with the help of simulation functions (see [10, 11]). Very recently, Aydi et al. [22] have presented the ω-interpolative Ćirić–Reich–Rus-type contractions by including in the contractivity condition some new terms and algebraic structures. This last class of contractive applications inspires some of the content that we will present in this paper.
Returning to the first commented line of research (employing only two terms in the contractive condition), last year Proinov [23] published a manuscript in which new results about existence and uniqueness of fixed points were demonstrated. This paper attracted much attention among researchers in this area, essentially due to the weak hypotheses that were used to develop the main results. For example, it was demonstrated that the involved Picard sequence was a Cauchy sequence without the need to establish monotonic conditions on the functions ψ and ϕ that appeared in the contractive condition. Furthermore, it was shown that a large number of contractions introduced by other authors (Amini-Harandi and Petrusel, Moradi, Geragthy, Jleli and Samet, Wardowski) could be seen as Proinov contractions.
In this paper, drawing inspiration from the above-mentioned works, we introduce a new class of contractions that generalize the Proinov contractions. Namely, we use a Ćirić–Reich–Rus type contractive condition in which new terms appear (distinct to the two used in the first discussed line of research). For this class of operators, we introduce new results about existence and uniqueness of fixed points. Furthermore, before that, we point out that this class properly extends the family of Proinov contractions since, specifically, we proved that all Proinov contractions are particular cases of the Roldán López de Hierro and Shahzad ample spectrum contractions.
2 Preliminaries
In this section we introduce the notation we are going to use, and we present the three classes of contractions in which this paper is inspired.
2.1 Algebraic background
The framework in which we will introduce our main results from now on is a metric space  endowed with a self-mapping
endowed with a self-mapping  . An element
. An element  such that
such that  is a fixed point of
is a fixed point of  . The set of all fixed points of
. The set of all fixed points of  is denoted by
is denoted by  .
.
Henceforth, let \(\mathbb{N}= \{ 1,2,3,\ldots \} \) stand for the set of all positive integer numbers. Following [24], a sequence  in
in  satisfying that
satisfying that  for all \(k,p\in \mathbb{N}\), \(k\neq p\), is called an infinite sequence. If
for all \(k,p\in \mathbb{N}\), \(k\neq p\), is called an infinite sequence. If  is given by
is given by  for all \(k\in \mathbb{N}\), then that sequence is known as a Picard sequence of
for all \(k\in \mathbb{N}\), then that sequence is known as a Picard sequence of  .
.
Proposition 1
([18], Proposition 2)
Let  be a Picard sequence in a metric space
be a Picard sequence in a metric space  such that
such that  . If there are \(k_{1},k_{2}\in \mathbb{N}\) such that \(k_{1}< k_{2}\) and
. If there are \(k_{1},k_{2}\in \mathbb{N}\) such that \(k_{1}< k_{2}\) and  , then there are \(k_{0}\in \mathbb{N}\) and
, then there are \(k_{0}\in \mathbb{N}\) and  such that
such that  for all \(k\geq k_{0}\) (that is,
for all \(k\geq k_{0}\) (that is,  is constant from a term onwards). In such a case,
is constant from a term onwards). In such a case,  is a fixed point of the self-mapping for which
is a fixed point of the self-mapping for which  is a Picard sequence.
is a Picard sequence.
Lemma 1
Let  be a sequence in a metric space
be a sequence in a metric space  such that
such that  as \(k\rightarrow +\infty \). If the sequence
as \(k\rightarrow +\infty \). If the sequence  is not
is not  -Cauchy, then there exist
-Cauchy, then there exist  and two partial subsequences
and two partial subsequences  and
and  of
of  such that
such that

2.2 Roldán–Shahzad ample spectrum contractions
In [15], Roldán López de Hierro and Shahzad introduced a great class of contractions that generalized many previous kinds of contractions with a particular property: they only used the terms  and
and  on their contractivity conditions. In the following definitions, \(\mathcal{S}\) represents a binary relation on
on their contractivity conditions. In the following definitions, \(\mathcal{S}\) represents a binary relation on  and \(\mathcal{S}^{\ast }\) is given by
and \(\mathcal{S}^{\ast }\) is given by  when
when  and
and  .
.
Definition 1
Let \(\{a_{k}\}\) and \(\{b_{k}\}\) be two sequences of real numbers. We say that \(\{ ( a_{k},b_{k} ) \}\) is a  -sequence if there exist two sequences
-sequence if there exist two sequences  such that
such that

Definition 2
([15], Definition 4)
We will say that  is an ample spectrum contraction if there exists a function
is an ample spectrum contraction if there exists a function  such that
such that  and ϱ satisfy the following four conditions:
and ϱ satisfy the following four conditions:
- \(( \mathcal{B}_{1} ) \):
-
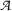 is nonempty and
is nonempty and 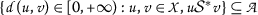 .
. - \(( \mathcal{B}_{2} ) \):
-
If
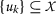 is a Picard \(\mathcal{S}\)-nondecreasing sequence of
is a Picard \(\mathcal{S}\)-nondecreasing sequence of 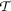 such that
such that 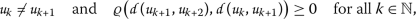
then
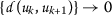 .
. - \(( \mathcal{B}_{3} ) \):
-
If
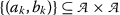 is a \((T,\mathcal{S}^{\ast })\)-sequence such that \(\{a_{k}\}\) and \(\{b_{k}\}\) converge to the same limit
is a \((T,\mathcal{S}^{\ast })\)-sequence such that \(\{a_{k}\}\) and \(\{b_{k}\}\) converge to the same limit  and verifying that
and verifying that 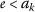 and \(\varrho (a_{k},b_{k})\geq 0\) for all \(k\in \mathbb{N}\), then
and \(\varrho (a_{k},b_{k})\geq 0\) for all \(k\in \mathbb{N}\), then 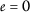 .
. - \(( \mathcal{B}_{4} ) \):
-
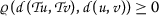 for all
for all 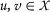 such that
such that 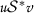 and
and 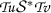 .
.
In such a case, we will say that  is an ample spectrum contraction with respect to \(\mathcal{S}\) and ϱ.
is an ample spectrum contraction with respect to \(\mathcal{S}\) and ϱ.
Some additional properties were taken into account in order to introduce very general results in the field of fixed point theory.
- \(( \mathcal{B}_{2}^{\prime } ) \):
-
If
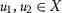 are two points such that
are two points such that 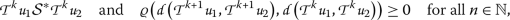
then
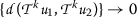 .
. - \(( \mathcal{B}_{5} ) \):
-
If \(\{ ( a_{k},b_{k} ) \}\) is a \((T,\mathcal{S}^{\ast })\)-sequence such that \(\{b_{k}\}\rightarrow 0\) and \(\varrho (a_{k},b_{k})\geq 0\) for all \(k\in \mathbb{N}\), then \(\{a_{k}\}\rightarrow 0\).
Although it was not explicitly enunciated in [15], we state here the following result which is a simple consequence of the main theorems given in [15]. The trivial binary relation \(\mathcal{S}_{X}\) on X is given by \(x\mathcal{S}_{X}y\) for all \(x,y\in X\).
Theorem 1
([15])
Each ample spectrum contraction w.r.t. \(\mathcal{S}_{X}\) from a complete metric space into itself satisfying \(( \mathcal{B}_{2}^{\prime } ) \) and \(( \mathcal{B}_{5} ) \) has a unique fixed point. In fact, each Picard sequence converges to such a fixed point.
Proof
The existence of fixed points follows from Theorem 2 in [15] using item \((b)\) and the uniqueness follows from Theorem 3 in [15] because we assume condition \(( \mathcal{B}_{2}^{\prime } ) \). □
2.3 ω-Interpolative Ćirić–Reich–Rus-type contractions
The notion of ω-interpolative Ćirić–Reich–Rus-type contraction was firstly inspired by the celebrated Kannan type contractions. A self-mapping  is a Kannan contraction if there is
is a Kannan contraction if there is  such that
such that

where  is a metric space. The reason why Kannan contractions were considered as an outstanding generalization of the Banach contractions lies in the fact that Kannan contractions are not necessarily continuous. Having in mind such kind of contractions and the concept of interpolation triple of type γ described in [19], Karapınar introduced in [20] the notion of interpolative Kannan type contraction, which corresponds to mappings
is a metric space. The reason why Kannan contractions were considered as an outstanding generalization of the Banach contractions lies in the fact that Kannan contractions are not necessarily continuous. Having in mind such kind of contractions and the concept of interpolation triple of type γ described in [19], Karapınar introduced in [20] the notion of interpolative Kannan type contraction, which corresponds to mappings  , from a metric space
, from a metric space  into itself, such that the following condition is fulfilled:
into itself, such that the following condition is fulfilled:

where α is a constant belonging to the interval \(( 0,1 ) \). This author was able to prove that each interpolative Kannan type contraction defined on a complete metric space has a unique fixed point.
Other significant advance in this line of study was the so-called α-admissible interpolative Rus–Reich–Ćirić type \(\mathcal{Z}\)-contractions which involve a contractivity condition as follows:

where

\(\zeta \in \mathcal{Z}\) is a simulation function (see [10, 11]), ψ and α are appropriate functions, and β and γ are positive constants such that \(\gamma +\beta <1\) (see [21] for more details).
Finally, it is worth mentioning the class of contractions that inspire this work. Following Definition 2 in [22], given a metric space  , a function
, a function  , two positive real \(\beta ,\gamma >0\) such that \(\beta +\gamma <1\), a function \(\psi \in \Psi \), we say that a mapping
, two positive real \(\beta ,\gamma >0\) such that \(\beta +\gamma <1\), a function \(\psi \in \Psi \), we say that a mapping  is an ω-interpolative Ćirić–Reich–Rus-type contraction if it verifies
is an ω-interpolative Ćirić–Reich–Rus-type contraction if it verifies

for all  . For the sake of completeness, we clarify that here Ψ represents the family of all nondecreasing functions \(\psi : [ 0, + \infty ) \rightarrow [ 0, + \infty ) \) satisfying the following condition:
. For the sake of completeness, we clarify that here Ψ represents the family of all nondecreasing functions \(\psi : [ 0, + \infty ) \rightarrow [ 0, + \infty ) \) satisfying the following condition:
Theorem 2
([22, Theorem 3])
Suppose that a continuous self-mapping  is ω-orbital admissible also an ω-interpolative Ćirić–Reich–Rus-type contraction on a complete metric space
is ω-orbital admissible also an ω-interpolative Ćirić–Reich–Rus-type contraction on a complete metric space  . If there is a point
. If there is a point  such that
such that  , then
, then  has a fixed point in
has a fixed point in  .
.
The notion of ω-orbital admissible mapping can be found in [22, 27].
2.4 Proinov contractions
Very recently, Proinov announced some results which unify many known results.
Theorem 3
(Proinov [23], Theorem 3.6)
Let  be a complete metric space and
be a complete metric space and  be a mapping such that
be a mapping such that

where the functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\) satisfy the following conditions:
- (\(a_{1}\)):
-
ψ is nondecreasing;
- (\(a_{2}\)):
-
\(\phi (s)<\psi (s)\) for any \(s>0\);
- (\(a_{3}\)):
-
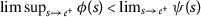 for any
for any 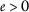 .
.
Then  has a unique fixed point
has a unique fixed point  and the iterative sequence
and the iterative sequence  converges to
converges to  for every
for every  .
.
3 \((\alpha ,\beta ,\psi ,\phi )\)-Interpolative contractions
As we have commented in the introduction, Theorem 3 has attracted the attention of many researchers in the field of fixed point theory due to the very weak hypotheses that are assumed in the statement in order to guarantee the existence and uniqueness of fixed points of the involved operator  . Furthermore, this author also showed in [23] that many fixed point results introduced along the last years in nonlinear analysis can be easily deduced from Theorem 3. Due to its great impact, we will say that a mapping
. Furthermore, this author also showed in [23] that many fixed point results introduced along the last years in nonlinear analysis can be easily deduced from Theorem 3. Due to its great impact, we will say that a mapping  from a metric space
from a metric space  into itself is a Proinov contraction if there are two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying the conditions (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), such that contractivity condition (2.1) holds. Theorem 3 guarantees that each Proinov contraction from a complete metric space into itself has a unique fixed point.Footnote 1 Inspired by this class of contractions and also by ω-interpolative Ćirić–Reich–Rus-type contractions [22], in this paper we are going to study the existence and uniqueness of fixed points of self-mapping satisfying a more general contractivity condition.
into itself is a Proinov contraction if there are two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying the conditions (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), such that contractivity condition (2.1) holds. Theorem 3 guarantees that each Proinov contraction from a complete metric space into itself has a unique fixed point.Footnote 1 Inspired by this class of contractions and also by ω-interpolative Ćirić–Reich–Rus-type contractions [22], in this paper we are going to study the existence and uniqueness of fixed points of self-mapping satisfying a more general contractivity condition.
Definition 3
Let  be a metric space. A mapping
be a metric space. A mapping  is said to be an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction if there exist \(\alpha ,\beta \in [ 0,1 ) \) such that \(\alpha +\beta <1\) and a pair of functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\) such that:
is said to be an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction if there exist \(\alpha ,\beta \in [ 0,1 ) \) such that \(\alpha +\beta <1\) and a pair of functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\) such that:

Although at a first sight contractivity condition (3.1) seems to be similar to (2.1), we would like to highlight that they are definitively distinct in nature. The main difference lies in the fact that contractive condition (2.1) only uses the terms  and
and  , while in condition (3.1) the terms
, while in condition (3.1) the terms  and
and  also appear. This fact forces us to assume that the initial points
also appear. This fact forces us to assume that the initial points  and
and  that are used in contractivity condition (3.1) are not fixed points of the mapping
that are used in contractivity condition (3.1) are not fixed points of the mapping  , since the function ϕ is not defined for \(t=0\). Furthermore, in such a case, if \(\alpha =0\) and
, since the function ϕ is not defined for \(t=0\). Furthermore, in such a case, if \(\alpha =0\) and  is a fixed point of
is a fixed point of  , the argument of ϕ in the right-hand side of (3.1) could contain an algebraic indetermination of type 00. To show that this difference is very important, we start our main results by showing that each Proinov contraction is an ample spectrum contraction.
, the argument of ϕ in the right-hand side of (3.1) could contain an algebraic indetermination of type 00. To show that this difference is very important, we start our main results by showing that each Proinov contraction is an ample spectrum contraction.
Theorem 4
Let  be a Proinov contraction from a metric space
be a Proinov contraction from a metric space  into itself associated with the functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\). Let us define:
into itself associated with the functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\). Let us define:
-
the binary relation \(\mathcal{S}_{X}\) on X given by
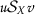 for all
for all 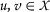 ,
, -
\(A=(0, + \infty )\),
-
\(\varrho _{\psi ,\phi }:(0, + \infty )\times (0, + \infty )\rightarrow \mathbb{R}\),
$$\begin{aligned}& \varrho _{\psi ,\phi }(t,s)=\phi ( s ) - \psi ( t ) \quad \textit{for all }t,s\in (0, + \infty ). \end{aligned}$$
Then  is an ample spectrum contraction with respect to \(\mathcal{S}\) and \(\varrho _{\psi ,\phi }\) satisfying additional properties \(( \mathcal{B}_{2}^{\prime } ) \) and \(( \mathcal{B}_{5} ) \).
is an ample spectrum contraction with respect to \(\mathcal{S}\) and \(\varrho _{\psi ,\phi }\) satisfying additional properties \(( \mathcal{B}_{2}^{\prime } ) \) and \(( \mathcal{B}_{5} ) \).
Proof
We check all the assumptions given in Definition 2.
- \(( \mathcal{B}_{1} ) \):
-
It is trivial because \(A=(0, + \infty )\).
- \(( \mathcal{B}_{2} ) \):
-
Let
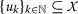 be a Picard \(\mathcal{S}\)-nondecreasing sequence of
be a Picard \(\mathcal{S}\)-nondecreasing sequence of 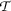 such that
such that 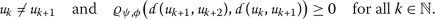
Then Lemma 2 implies that
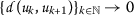 .
. - \(( \mathcal{B}_{2}^{\prime } ) \):
-
Let
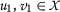 be two initial points such that the Picard sequences
be two initial points such that the Picard sequences 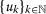 and
and 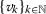 , defined by
, defined by 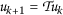 and
and 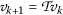 for all \(k\in \mathbb{N}\), satisfy
for all \(k\in \mathbb{N}\), satisfy 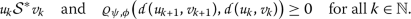
Therefore, for all \(k\in \mathbb{N}\),
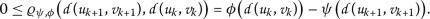
Taking into account condition \((a_{2})\) and the fact that
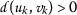 , the previous inequality means that
, the previous inequality means that 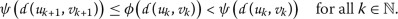 (3.2)
(3.2)Since the function ψ is nondecreasing, then
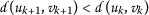 for all \(k\in \mathbb{N}\). Let
for all \(k\in \mathbb{N}\). Let 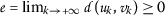 . Notice that
. Notice that 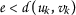 for all \(k\in \mathbb{N}\). To prove that
for all \(k\in \mathbb{N}\). To prove that 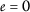 , assume that
, assume that 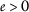 . In this case the following limits are equal:
. In this case the following limits are equal: 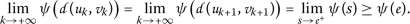
Then (3.2) leads to
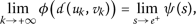
which contradicts (\(a_{3}\)) because
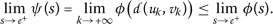
As a consequence,
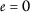 , that is,
, that is,  .
. - \(( \mathcal{B}_{2} ) \):
-
It directly follows from \(( \mathcal{B}_{2}^{\prime } ) \) by choosing an arbitrary point
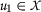 and using
and using 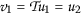 in \(( \mathcal{B}_{2}^{\prime } ) \).
in \(( \mathcal{B}_{2}^{\prime } ) \). - \(( \mathcal{B}_{3} ) \):
-
Let \(\{ ( a_{k},b_{k} ) \}\subseteq A\times A\) be a
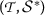 -sequence such that \(\{a_{k}\}\) and \(\{b_{k}\}\) converge to the same limit
-sequence such that \(\{a_{k}\}\) and \(\{b_{k}\}\) converge to the same limit 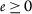 and verifying that
and verifying that 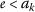 and \(\varrho _{\psi ,\phi }(a_{k},b_{k})\geq 0\) for all \(k\in \mathbb{N}\). Therefore, for all \(k\in \mathbb{N}\), \(0\leq \varrho _{\psi ,\phi }(a_{k},b_{k})=\phi ( b_{k} ) - \psi ( a_{k} ) \), so \(\psi ( a_{k} ) \leq \phi ( b_{k} ) \). Since \(a_{k}>0\) and \(b_{k}>0\), then (\(a_{2}\)) implies that $$ \psi ( a_{k} ) \leq \phi ( b_{k} ) < \psi ( b_{k} ) \quad \text{for all }k\in \mathbb{N}. $$(3.3)
and \(\varrho _{\psi ,\phi }(a_{k},b_{k})\geq 0\) for all \(k\in \mathbb{N}\). Therefore, for all \(k\in \mathbb{N}\), \(0\leq \varrho _{\psi ,\phi }(a_{k},b_{k})=\phi ( b_{k} ) - \psi ( a_{k} ) \), so \(\psi ( a_{k} ) \leq \phi ( b_{k} ) \). Since \(a_{k}>0\) and \(b_{k}>0\), then (\(a_{2}\)) implies that $$ \psi ( a_{k} ) \leq \phi ( b_{k} ) < \psi ( b_{k} ) \quad \text{for all }k\in \mathbb{N}. $$(3.3)As ψ is nondecreasing, \(a_{k}< b_{k}\), so
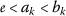 for all \(k\in \mathbb{N}\). Taking into account that
for all \(k\in \mathbb{N}\). Taking into account that 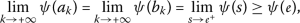
property (3.3) leads to
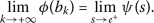
However, if
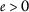 , we deduce a contradiction with (\(a_{3}\)) because
, we deduce a contradiction with (\(a_{3}\)) because 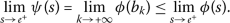
Therefore,
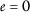 .
. - \(( \mathcal{B}_{4} ) \):
-
Let
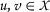 be such that
be such that 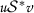 and
and 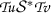 , that is,
, that is, 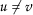 and
and 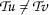 . Therefore contractivity condition (2.1) implies that
. Therefore contractivity condition (2.1) implies that 
- \(( \mathcal{B}_{5} ) \):
-
Let \(\{ ( a_{k},b_{k} ) \}\) be a \((T,\mathcal{S}^{\ast })\)-sequence such that \(\{b_{k}\}\rightarrow 0\) and \(\varrho _{\psi ,\phi }(a_{k},b_{k})\geq 0\) for all \(k\in \mathbb{N}\). We can repeat the argument of (3.3), so we deduce that \(a_{k}< b_{k}\) for all \(k\in \mathbb{N}\). Hence \(\{a_{k}\}\rightarrow 0\). □
Corollary 1
Each Proinov contraction is an ample spectrum contraction.
Corollary 2
Theorem 3directly follows from Theorem 1.
Theorem 4 implies that \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contractions belong to a category of contractions that are very distinct in nature to the class of Proinov contractions: each Proinov contraction is a particular case of an ample spectrum contraction; however, for the moment, it is an open problem to study the possible relationship between \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contractions and ample spectrum contractions.
4 Fixed point theorems for \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contractions
In this section we introduce some fixed point results for \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contractions. The following lemma is important in order to show later that a Picard sequence is Cauchy.
Lemma 2
Let  be an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction from a metric space
be an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction from a metric space  into itself, and suppose that the functions ϕ and ψ satisfy, at least, one of the following conditions:
into itself, and suppose that the functions ϕ and ψ satisfy, at least, one of the following conditions:
- (\(\mathbb{A}\)):
-
It holds, at the same time,
- (\(a_{1}\)):
-
ψ is nondecreasing,
- (\(a_{2}\)):
-
\(\phi (s)<\psi (s)\) for all \(s>0\),
- (\(a_{3}\)):
-
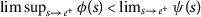 for all
for all 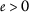 .
.
- (\(\mathbb{B}\)):
-
If \(\{s_{n}\}\subset ( 0, + \infty ) \) is a sequence such that \(\psi ( s_{k+1} ) \leq \phi (s_{k}^{1-\beta }s_{k+1}^{ \beta })\) for all \(k\in \mathbb{N}\), then \(\{s_{k}\}\rightarrow 0\).
Then  is an asymptotically regular mapping.
is an asymptotically regular mapping.
Proof
Let  be arbitrary, and let us define
be arbitrary, and let us define  and
and  for all \(k\in \mathbb{N}\). If there is \(k_{0}\in \mathbb{N}\) such that
for all \(k\in \mathbb{N}\). If there is \(k_{0}\in \mathbb{N}\) such that  , then
, then  is a fixed point of
is a fixed point of  . In such a case,
. In such a case,  . On the contrary, suppose that
. On the contrary, suppose that  for all \(k\in \mathbb{N}\). Then each
for all \(k\in \mathbb{N}\). Then each  is not a fixed point of
is not a fixed point of  and also
and also

Applying contractivity condition (3.1), we deduce that, for all \(k\in \mathbb{N}\),

If we define  for all \(k\in \mathbb{N}\), the previous inequality means that the sequence \(\{s_{k}\}\) satisfies \(\psi ( s_{k+1} ) \leq \phi (s_{k}^{1-\beta }s_{k+1}^{ \beta })\) for all \(k\in \mathbb{N}\). Under condition (\(\mathbb{B}\)), we deduce that
for all \(k\in \mathbb{N}\), the previous inequality means that the sequence \(\{s_{k}\}\) satisfies \(\psi ( s_{k+1} ) \leq \phi (s_{k}^{1-\beta }s_{k+1}^{ \beta })\) for all \(k\in \mathbb{N}\). Under condition (\(\mathbb{B}\)), we deduce that  , and this completes the proof.
, and this completes the proof.
Next, suppose that (\(\mathbb{A}\)) holds. Since  and
and  , property (\(a_{2}\)) guarantees that, for all \(k\in \mathbb{N}\),
, property (\(a_{2}\)) guarantees that, for all \(k\in \mathbb{N}\),

Taking into account that the function ψ is nondecreasing, it follows that

which immediately leads to

As the sequence of positive real numbers  is strictly decreasing, it is convergent. Then there is
is strictly decreasing, it is convergent. Then there is  such that
such that

To prove that  , we assume, by contradiction, that
, we assume, by contradiction, that  . In this case, both sequences,
. In this case, both sequences,

are strictly decreasing and converging to  (notice that if \(\beta =0\), then
(notice that if \(\beta =0\), then  for all \(k\in \mathbb{N}\)). As ψ is nondecreasing, the following limits exist and they are equal:
for all \(k\in \mathbb{N}\)). As ψ is nondecreasing, the following limits exist and they are equal:

As a consequence, letting \(k\rightarrow + \infty \) in (4.1), the following limit exists and it is finite:

However, this fact contradicts the property (\(a_{3}\)) because

As a consequence,  and
and  is an asymptotically regular mapping. □
is an asymptotically regular mapping. □
Remark 1
-
1
Notice that the previous result shows that condition (ii) is not necessary in [23, Lemma 3.2] when we suppose that (iii) holds.
-
2
We include assumption (\(\mathbb{B}\)) in the previous result because it can be easy to check in practical examples. For instance, if there is \(\lambda \in [ 0,1 ) \) such that \(\psi (s)=s\) and \(\phi (s)=\lambda s\) for all \(s\in ( 0, + \infty ) \), then (\(\mathbb{B}\)) trivially holds and we do not need to check the properties given in (\(\mathbb{A}\)).
Our first main theorem in this paper is the following result.
Theorem 5
Let  be an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction from a complete metric space
be an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction from a complete metric space  into itself, and suppose that the functions ϕ and ψ satisfy the following properties:
into itself, and suppose that the functions ϕ and ψ satisfy the following properties:
- (\(a_{1}\)):
-
ψ is nondecreasing,
- (\(a_{2}\)):
-
\(\phi (s)<\psi (s)\) for all \(s>0\),
- (\(a_{3}\)):
-
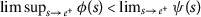 for all
for all 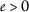 .
.
Then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
First of all, let us prove that  is not fixed-points free. Let
is not fixed-points free. Let  be an arbitrary initial point, and let us consider the Picard sequence
be an arbitrary initial point, and let us consider the Picard sequence  of
of  starting from
starting from  , that is, define
, that is, define  and
and  for all \(k\in \mathbb{N}\). If there is \(k_{0}\in \mathbb{N}\) such that
for all \(k\in \mathbb{N}\). If there is \(k_{0}\in \mathbb{N}\) such that  , then
, then  is a fixed point of
is a fixed point of  . In this case, the first part of the proof is finished. Next suppose that
. In this case, the first part of the proof is finished. Next suppose that  for all \(k\in \mathbb{N}\). Hence Lemma 2 implies that
for all \(k\in \mathbb{N}\). Hence Lemma 2 implies that

Furthermore, Proposition 1 guarantees that each two terms of the Picard sequence  are distinct, that is,
are distinct, that is,  for any \(k_{1},k_{2}\in \mathbb{N}\) such that \(k_{1}\neq k_{2}\).
for any \(k_{1},k_{2}\in \mathbb{N}\) such that \(k_{1}\neq k_{2}\).
In order to prove that  is a
is a  -Cauchy sequence, we reason by contradiction. Suppose that
-Cauchy sequence, we reason by contradiction. Suppose that  is not
is not  -Cauchy. In such a case, Lemma 1 states that there exist
-Cauchy. In such a case, Lemma 1 states that there exist  and two partial subsequences
and two partial subsequences  and
and  of
of  such that
such that


Applying contractivity condition (3.1) and property (\(a_{2}\)), we deduce that, for all \(k\in \mathbb{N}\),

Since ψ is nondecreasing, then, for all \(k\in \mathbb{N}\),

which, in particular, means that, for all \(k\in \mathbb{N}\),

Taking into account (4.2)–(4.4), notice that

If \(\alpha >0\) or \(\beta >0\), then, letting \(k\rightarrow + \infty \) in (4.5), we observe that

which contradicts the fact that  . To avoid this contradiction, assume that \(\alpha =\beta =0\). In such a case, contractivity condition (3.1) is given by
. To avoid this contradiction, assume that \(\alpha =\beta =0\). In such a case, contractivity condition (3.1) is given by

Although this condition is more general than condition (3.1) given in [23], the same arguments of the proof of Lemma 3.3 in that paper show that  is a Cauchy sequence in
is a Cauchy sequence in  . Hence, we have proved that, in any case, the sequence
. Hence, we have proved that, in any case, the sequence  is
is  -Cauchy in the complete metric space
-Cauchy in the complete metric space  . As a consequence, there is
. As a consequence, there is  such that
such that  , that is,
, that is,

We claim that  . To prove it, assume by contradiction that
. To prove it, assume by contradiction that  , that is,
, that is,  . As the sequence
. As the sequence  is infinite, then there is \(k_{0}\in \mathbb{N}\) such that
is infinite, then there is \(k_{0}\in \mathbb{N}\) such that  and
and  for all \(k\geq k_{0}\). Using contractivity condition (3.1) and property (\(a_{2}\)), we deduce that, for all \(k\geq k_{0}\),
for all \(k\geq k_{0}\). Using contractivity condition (3.1) and property (\(a_{2}\)), we deduce that, for all \(k\geq k_{0}\),

Since ψ is nondecreasing, we deduce that

Since \(1-\alpha -\beta >0\), then  , so
, so  . Hence the uniqueness of the limit of the sequence
. Hence the uniqueness of the limit of the sequence  in the metric space
in the metric space  guarantees that
guarantees that  , which is a contradiction because we have assumed that
, which is a contradiction because we have assumed that  is not a fixed point of
is not a fixed point of  .
.
This contradiction finally proves that  is a fixed point of
is a fixed point of  and, also, that the Picard sequence
and, also, that the Picard sequence  converges to such a fixed point whatever the initial point
converges to such a fixed point whatever the initial point  . □
. □
In general, the uniqueness of the fixed point is not guaranteed. In fact, contractivity condition (3.1) that an \((\alpha ,\beta ,\psi ,\phi )\)-interpolative mapping satisfies cannot be employed to establish a relationship between any two distinct fixed points. The problem of condition

is that the functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\) are not necessarily defined for \(t=0\). Therefore, if  (or
(or  ) is a fixed point of
) is a fixed point of  , then the right-hand side of the previous inequality is not well defined. On the one hand, when ψ is nondecreasing, the limit
, then the right-hand side of the previous inequality is not well defined. On the one hand, when ψ is nondecreasing, the limit
exists but it could take the value −∞ when the function ψ is not bounded from below. Avoiding this last case, it seems reasonable to assume that ψ is well defined on \(t=0\). On the other hand, there is not a clear constraint about the possible value of \(\phi ( 0 ) \) because the condition \(\phi <\psi \) does not lead to an additional condition unless we assume that both functions ϕ and ψ would be continuous at \(t=0\). In the following result we illustrate a simple way to deduce the uniqueness of the fixed point by assuming an additional condition.
Theorem 6
Given a mapping  from a complete metric space
from a complete metric space  into itself, suppose that there are two real numbers \(\alpha ,\beta \in [ 0,1 ) \) such that \(\alpha +\beta <1\) and a pair of functions \(\psi ,\phi : [ 0, + \infty ) \rightarrow \mathbb{R}\) satisfying
into itself, suppose that there are two real numbers \(\alpha ,\beta \in [ 0,1 ) \) such that \(\alpha +\beta <1\) and a pair of functions \(\psi ,\phi : [ 0, + \infty ) \rightarrow \mathbb{R}\) satisfying

for any  with
with  (we agree here that
(we agree here that  if \(\alpha =0\) and
if \(\alpha =0\) and  is a fixed point of
is a fixed point of  , and similarly with
, and similarly with  ). Additionally, assume that the following conditions are fulfilled:
). Additionally, assume that the following conditions are fulfilled:
- (\(a_{1}\)):
-
ψ is nondecreasing on \(( 0, + \infty ) \);
- (\(a_{2}\)):
-
\(\phi (s)<\psi (s)\) for all \(s>0\);
- (\(a_{3}\)):
-
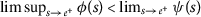 for all
for all 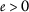 ;
; - (\(a_{4}\)):
-
if \(s_{0}\in [ 0, + \infty ) \) verifies that \(\psi ( s_{0} ) \leq \phi ( 0 ) \), then \(s_{0}=0\).
Then  has a unique fixed point and the Picard sequence
has a unique fixed point and the Picard sequence  converges to such a fixed point of
converges to such a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
Let us consider the restricted functions \(\psi ^{\prime }=\psi| _{ ( 0, + \infty ) }\), \(\phi ^{\prime }=\phi| _{ ( 0, + \infty ) }: ( 0, + \infty ) \rightarrow \mathbb{R}\). Then  is an \((\alpha ,\beta ,\psi ^{\prime },\phi ^{\prime })\)-interpolative mapping. Since \(\psi ^{\prime }\) and \(\phi ^{\prime }\) satisfy the auxiliary conditions (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), Theorem 5 guarantees that the mapping
is an \((\alpha ,\beta ,\psi ^{\prime },\phi ^{\prime })\)-interpolative mapping. Since \(\psi ^{\prime }\) and \(\phi ^{\prime }\) satisfy the auxiliary conditions (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), Theorem 5 guarantees that the mapping  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  . To prove the uniqueness of the fixed point, suppose that there exist two distinct fixed points
. To prove the uniqueness of the fixed point, suppose that there exist two distinct fixed points  of
of  . Then
. Then  . In this case, the contractivity condition implies that
. In this case, the contractivity condition implies that

We can reason as follows to obtain a contradiction.
-
If \(\alpha >0\), then
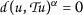 , and if \(\beta >0\), then
, and if \(\beta >0\), then 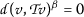 . In both cases,
. In both cases,  . However, assumption (\(a_{4}\)) would imply that
. However, assumption (\(a_{4}\)) would imply that  , which contradicts the fact that
, which contradicts the fact that 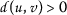 .
. -
If \(\alpha =\beta =0\), then (4.7) means that
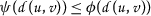 , which contradicts (\(a_{2}\)) because
, which contradicts (\(a_{2}\)) because  .
.
In any case, the obtained contradiction leads to the uniqueness of the fixed point of  . □
. □
Next we show some consequences of the previous main results.
Corollary 3
Let  be a complete metric space, and let
be a complete metric space, and let  be a mapping. Suppose that there exist a constant \(\alpha \in ( 0,1 ) \) and two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying (\(a_{1} \)), (\(a_{2}\)), and (\(a_{3}\)), such that
be a mapping. Suppose that there exist a constant \(\alpha \in ( 0,1 ) \) and two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying (\(a_{1} \)), (\(a_{2}\)), and (\(a_{3}\)), such that

Then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
It follows from Theorem 5 applied to the case \(\beta =0\). □
We can easily deduce the Proinov theorem even if we assume that  .
.
Corollary 4
Let  be a complete metric space, and let
be a complete metric space, and let  be a mapping. Suppose that there exist two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), such that
be a mapping. Suppose that there exist two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), such that

Then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
It follows from Theorem 5 applied to the case \(\alpha =\beta =0\). □
Corollary 5
Let  be a complete metric space, and let
be a complete metric space, and let  be a mapping. Suppose that there exist a constant \(\alpha \in ( 0,0.5 ) \) and two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), such that
be a mapping. Suppose that there exist a constant \(\alpha \in ( 0,0.5 ) \) and two functions \(\psi ,\phi :(0, + \infty )\rightarrow \mathbb{R}\), satisfying (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)), such that

Then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
It corresponds to the case \(\alpha =\beta \) in Theorem 5. □
Corollary 6
Let  be a complete metric space, let
be a complete metric space, let  be a mapping, and let \(\phi :(0, + \infty )\rightarrow \mathbb{R}\) be a function satisfying the following conditions:
be a mapping, and let \(\phi :(0, + \infty )\rightarrow \mathbb{R}\) be a function satisfying the following conditions:
- (\(a_{2}\)):
-
\(\phi (s)< s\) for all \(s>0\);
- (\(a_{3}\)):
-
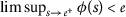 for all
for all 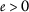 .
.
If we assume that there exist two constants \(\alpha ,\beta \in ( 0,1 ) \) such that \(\alpha +\beta <1\) and

then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
It is only necessary to apply Theorem 5 when \(\psi (s)=s \) for all \(s\in (0, + \infty )\). □
Corollary 7
Let  be a complete metric space, let
be a complete metric space, let  be a mapping, and let \(\psi :(0, + \infty )\rightarrow \mathbb{R}\) be a function satisfying the following conditions:
be a mapping, and let \(\psi :(0, + \infty )\rightarrow \mathbb{R}\) be a function satisfying the following conditions:
- (\(a_{1}\)):
-
ψ is nondecreasing on \(( 0, + \infty ) \);
- (\(a_{2}\)):
-
\(s<\psi (s)\) for all \(s>0\).
If we assume that there exist two constants \(\alpha ,\beta \in ( 0,1 ) \) such that \(\alpha +\beta <1\) and

then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
We use the function \(\phi :(0, + \infty )\rightarrow \mathbb{R}\) defined by \(\phi (s)=s\) for all \(s\in (0, + \infty )\). Notice that, in this case, for all  ,
,

so assumption (\(a_{3}\)) can be deduced from (\(a_{1}\)) and (\(a_{2}\)). Therefore, it is only necessary to apply Theorem 5 when \(\phi (s)=s\) for all \(s\in (0, + \infty )\). □
Corollary 8
Let  be a complete metric space, and let
be a complete metric space, and let  be a mapping. Assume that there exist three constants
be a mapping. Assume that there exist three constants  such that \(\alpha +\beta <1\) and
such that \(\alpha +\beta <1\) and

then  has a fixed point and the Picard sequence
has a fixed point and the Picard sequence  converges to a fixed point of
converges to a fixed point of  whatever the initial point
whatever the initial point  .
.
Proof
This result follows from Theorem 5 by using \(\psi (s)=s\) and  for all \(s\in (0, + \infty )\). Such functions clearly satisfy conditions (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)). □
for all \(s\in (0, + \infty )\). Such functions clearly satisfy conditions (\(a_{1}\)), (\(a_{2}\)), and (\(a_{3}\)). □
5 Conclusions and prospect work
Inspired by two well-known families of contractions, namely, Proinov contractions and ω-interpolative Ćirić–Reich–Rus-type contractions, in this paper we have introduced the notion of \((\alpha ,\beta ,\psi ,\phi )\)-interpolative contraction as a way to take advantage of the best properties of both classes of contractive mappings. Furthermore, we have shown that this new kind of contractions is distinct in nature to the previous definitions, which provides substantial added value to our proposal compared to the above-mentioned families.
In prospect work we will study the possible relationships between this novel class of contractions and other families of contractive mappings, mainly in order to search for new applications, and we will also try to generalize them by employing more general conditions, auxiliary functions, and algebraic structures.
Availability of data and materials
The data and material used to support the findings of this study are included within the article.
Notes
Notice that this author forgot to include the completeness of the metric space in his main results in [23].
References
Boyd, D.W., Wong, J.S.W.: On nonlinear contractions. Proc. Am. Math. Soc. 20, 458–464 (1969)
Geraghty, M.: On contractive mappings. Proc. Am. Math. Soc. 40, 604–608 (1973)
Amini-Harandi, A., Petruşel, A.: A fixed point theorem by altering distance technique in complete metric spaces. Miskolc Math. Notes 14, 11–17 (2013)
Jleli, M., Samet, B.: A new generalization of the Banach contraction principle. J. Inequal. Appl. 2014, 38 (2014)
Wardowski, D.: Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, Article ID 94 (2012)
Banach, S.: Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 3(1), 133–181 (1922)
Al-Mezel, S.A., Alsulami, H.H., Karapınar, E., Roldán López de Hierro, A.F.: Discussion on “multidimensional coincidence points” via recent publications. Abstr. Appl. Anal. 2014, Article ID 287492 (2014)
Roldán López de Hierro, A.F., Karapınar, E., Manro, S.: Some new fixed point theorems in fuzzy metric spaces. J. Intell. Fuzzy Syst. 27(5), 2257–2264 (2014)
Roldán, A., Martínez-Moreno, J., Roldán, C.: On interrelationships between fuzzy metric structures. Iran. J. Fuzzy Syst. 10(2), 133–150 (2013)
Khojasteh, F., Shukla, S., Radenović, S.: A new approach to the study of fixed point theorems via simulation functions. Filomat 29(6), 1189–1194 (2015)
Roldán López de Hierro, A.F., Karapınar, E., Roldán López de Hierro, C., Martínez-Moreno, J.: Coincidence point theorems on metric spaces via simulation functions. J. Comput. Appl. Math. 275, 345–355 (2015)
Roldán López de Hierro, A.F., Shahzad, N.: New fixed point theorem under R-contractions. Fixed Point Theory Appl. 2015, Article ID 345 (2015)
Roldán López de Hierro, A.F., Shahzad, N.: Common fixed point theorems under \((\mathcal{R},\mathcal{S})\)-contractivity conditions. Fixed Point Theory Appl. 2016, Article ID 55 (2016)
Shahzad, N., Roldán López de Hierro, A.F., Khojasteh, F.: Some new fixed point theorems under \((\mathcal{A},\mathcal{S})\)-contractivity conditions. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 111(2), 307–324 (2017)
Roldán López de Hierro, A.F., Shahzad, N.: Ample spectrum contractions and related fixed point theorems. Mathematics 7, 1033 (2019)
Kannan, R.: Some results on fixed points. Bull. Calcutta Math. Soc. 60, 71–76 (1968)
Kannan, R.: Some results on fixed points II. Am. Math. Mon. 76, 405–408 (1969)
Roldán López de Hierro, A.F., Karapınar, E., Fulga, A.: Multiparametric contractions and related Hardy–Roger type fixed point theorems. Mathematics 8(6), Article ID 957 (2020)
Krein, S.G., Petunin, J.I., Semenov, E.M.: Interpolation of Linear Operators. Am. Math. Soc., Providence (1978)
Karapınar, E.: Revisiting the Kannan type contractions via interpolation. Adv. Theory Nonlinear Anal. Appl. 2(2), 85–87 (2018)
Agarwal, R.P., Karapınar, E.: Interpolative Rus–Reich–Ćirić type contractions via simulation functions. An. Ştiinţ. Univ. ‘Ovidius’ Constanţa 27(3), 137–152 (2019)
Aydi, H., Karapınar, E., Roldán López de Hierro, A.F.: ω-Interpolative Ćirić–Reich–Rus-type contractions. Mathematics 7(1), Article ID 57 (2019)
Proinov, P.D.: Fixed point theorems for generalized contractive mappings in metric spaces. J. Fixed Point Theory Appl. 22, 21 (2020)
Roldán López de Hierro, A.F., Shahzad, N.: Fixed point theorems by combining Jleli and Samet’s, and Branciari’s inequalities. J. Nonlinear Sci. Appl. 9, 3822–3849 (2016)
Agarwal, R.P., Karapınar, E., O’Regan, D., Roldán López de Hierro, A.F.: Fixed Point Theory in Metric Type Spaces. Springer, Berlin (2015)
Karapınar, E., Roldán, A., Martínez-Moreno, J., Roldán, C.: Meir–Keeler type multidimensional fixed point theorems in partially ordered metric spaces. Abstr. Appl. Anal. 2013, Article ID 406026 (2013)
Popescu, O.: Some new fixed point theorems for α-Geraghty contraction type maps in metric spaces. Fixed Point Theory Appl. 2014, Article ID 190 (2014)
Acknowledgements
The authors thank their universities. A.F. Roldán López de Hierro is grateful to Junta de Andalucía by project FQM-365 of the Andalusian CICYE and to Ministerio de Ciencia e Innovación by project PID2020-119478GB-I00.
Funding
We declare that funding is not applicable for our paper.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karapınar, E., Fulga, A. & Roldán López de Hierro, A.F. Fixed point theory in the setting of \((\alpha,\beta,\psi,\phi)\)-interpolative contractions. Adv Differ Equ 2021, 339 (2021). https://doi.org/10.1186/s13662-021-03491-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03491-w
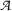 is nonempty and
is nonempty and 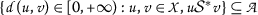 .
.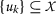 is a Picard
is a Picard 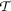 such that
such that 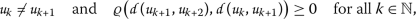
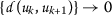 .
.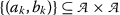 is a
is a  and verifying that
and verifying that 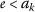 and
and 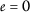 .
.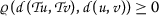 for all
for all 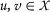 such that
such that 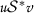 and
and 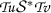 .
.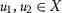 are two points such that
are two points such that 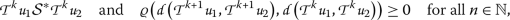
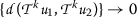 .
.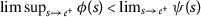 for any
for any 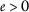 .
.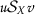 for all
for all 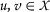 ,
,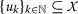 be a Picard
be a Picard 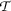 such that
such that 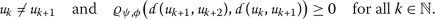
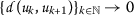 .
.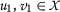 be two initial points such that the Picard sequences
be two initial points such that the Picard sequences 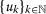 and
and 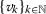 , defined by
, defined by 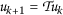 and
and 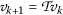 for all
for all 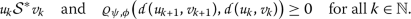
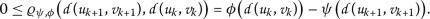
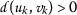 , the previous inequality means that
, the previous inequality means that 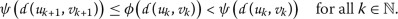
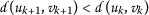 for all
for all 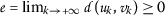 . Notice that
. Notice that 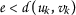 for all
for all 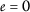 , assume that
, assume that 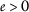 . In this case the following limits are equal:
. In this case the following limits are equal: 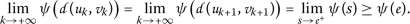
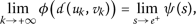
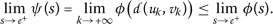
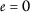 , that is,
, that is,  .
.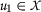 and using
and using 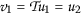 in
in 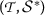 -sequence such that
-sequence such that 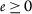 and verifying that
and verifying that 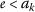 and
and 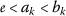 for all
for all 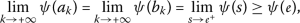
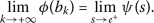
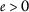 , we deduce a contradiction with (
, we deduce a contradiction with (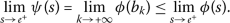
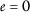 .
.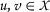 be such that
be such that 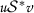 and
and 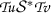 , that is,
, that is, 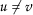 and
and 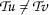 . Therefore contractivity condition (
. Therefore contractivity condition (
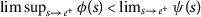 for all
for all 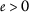 .
.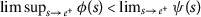 for all
for all 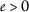 .
.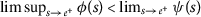 for all
for all 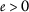 ;
;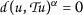 , and if
, and if 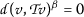 . In both cases,
. In both cases,  . However, assumption (
. However, assumption ( , which contradicts the fact that
, which contradicts the fact that 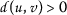 .
.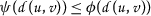 , which contradicts (
, which contradicts ( .
.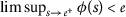 for all
for all 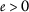 .
.