- Research
- Open access
- Published:
On fractional neutral integro-differential systems with state-dependent delay and non-instantaneous impulses
Advances in Difference Equations volume 2015, Article number: 372 (2015)
Abstract
In this manuscript, we work to actualize the Darbo (Banas and Goebel in Measure of Noncompactness in Banach Space. Lecture Notes in Pure and Applied Mathematics, 1980) fixed point theorem (FPT) coupled with the Hausdorff measure of non-compactness to analyze the existence results for an impulsive fractional neutral integro-differential equation (IFNIDE) with state-dependent delay (SDD) and non-instantaneous impulses (NII) in Banach spaces. Finally, examples are offered to demonstrate the concept.
1 Introduction
Throughout this manuscript, we set up the existence of mild solutions for IFNIDE with SDD and NII in Banach spaces through the utilization of the FPT thanks to Darbo [1]. We discuss the impulsive neutral integro-differential equations of fractional-order of the model
where \({}^{\mathrm{C}}D_{t}^{\alpha}\) is the Caputo fractional derivative of order \(\alpha \in(0,1)\), and \(\mathscr{I}=[0,T]\) is an operational interval. The operator \(-\mathscr{A}\) denotes the infinitesimal generator of an analytic semigroup \(\{\mathbb{T}(t)\}_{t\ge0}\) in a Banach space \(\mathbb{X}\) having norm \(\|\cdot\|\), this suggests that we can find \(\mathcal{M}\ge1\) to ensure that \(\| \mathbb{T}(t)\|\le \mathcal{M}\), \(\mathscr{F}:\mathscr{I}\times{\mathscr{B}}_{h}\times \mathbb{X}\rightarrow\mathbb{X}\), \(e:\mathscr {D}\times{\mathscr{B}}_{h}\rightarrow\mathbb{X}\), \(\mathscr {G}:\mathscr{I}\times{\mathscr {B}}_{h}\rightarrow\mathbb{X}\), \(\varrho:\mathscr{I}\times{\mathscr {B}}_{h}\rightarrow (-\infty,T]\) are apposite functions, and \({\mathscr{B}}_{h}\) is a phase space characterized in preliminaries. Here \(\mathscr{D}=\{ (t,s)\in \mathscr{I}\times\mathscr{I}: 0\le s\le t\le T\}\). Here \(0=t_{0}=s_{0}< t_{1}\le s_{1}< t_{2}\le s_{2}<\cdots<t_{N}\le s_{N}<t_{N+1}=T\), are prefixed numbers, and \(g_{i}\in C((t_{i},s_{i}]\times{\mathscr{B}}_{h},\mathbb{X})\), for all \(i=1,2,\ldots,N\), stand for impulsive conditions.
For almost any continuous function x characterized on \((-\infty,T]\) and for almost any \(t\ge0\), we designate by \(x_{t}\) the part of \({\mathscr{B}}_{h}\) characterized by \(x_{t}(\theta)=x(t+\theta)\) for \(\theta\le0\). Now \(x_{t}(\cdot)\) refers to the historical backdrop of the state from every \(\theta\in(-\infty,0]\) like the current time t.
Fractional differential equations (FDE) are broadly successfully utilized in science and engineering. For fundamental results as regards the fractional systems, the reader should check [2, 3] and [4–19], as well as the references cited therein. Fractional equations with delay features appear in several areas, such as the medical and physical fields with state-dependent delay or non-constant delay. Recently, the existence results of mild solutions for such problems became very attractive and several researchers are working on it; see for instance [20–25]. As a result some papers were released on the fractional/integer order problems having SDD and NII [26–29].
The investigation of impulsive functional differential or integro-differential frameworks is interesting for their application in strengthening techniques and phenomena conditional on short-time perturbations in the course of their progress. The perturbations are conducted separately and their term is insignificant in correlation with the aggregate length of time of the procedures. For more details as regards this concept and its uses, see for example the treatise by Lakshmikantham et al. [30], Stamova [31], Graef et al. [32], Bainov and Covachev [33], Benchohra et al. [34] and [35–44], and the references cited therein.
We recall that numerous impulsive frameworks emerging from sensible models can be depicted as partial differential equations with NII. As pointed out in [36, 37], there are various ways to investigate this sort of models. Also, Kumar et al. [45] analyzed the existence of solutions for FDE with NII in Banach spaces through the utilization of the appropriate FPT. Gautam and Dabas [26, 27] acknowledged the existence of mild solutions for FIDE with SDD and NII through the employment of the suitable FPT. Later Das et al. [28, 29] researched the existence of mild solution of a class of second order partial neutral differential equations with SDD and NII in Banach spaces. The results are obtained through the utilization of the Hausdorff measures of non-compactness and Darbo FPT. However, the existence results for IFIDE with SDD and NII in \(\mathscr {B}_{h}\) phase space contexts have not yet been completely examined. This motivated us to investigate the existence results of the system (1.1) with NII in Banach spaces. To the best of our knowledge the existence results for the considered model (1.1)-(1.3) in the present manuscript are new.
In contrast to the current outcomes, this manuscript has some positive aspects, namely: We include the integral term in the non-linear term \(\mathscr{F}\) and present an appropriate notion of a mild solution of the model (1.1)-(1.3). Then we analyze the existence of mild solutions for IFIDE with SDD and NII of the design (1.1)-(1.3) under the Darbo [1] fixed point theorem, and the results in [27] might be regarded as special circumstances. After that, we implement \({\mathscr {B}}_{h}\) phase space contexts to examine the model (1.1)-(1.3).
This manuscript is composed as follows. We demonstrate a couple of preliminaries, definitions, and lemmas which are to be employed in this fashion to exhibit our essential outcomes in Section 2. After that, the existence of mild solutions for the model (1.1)-(1.3) is analyzed under the Darbo [1] FPT in Section 3. Section 4 shows examples of the theoretical results.
2 Preliminaries
Below, we give some fundamental definitions, lemmas, and preparatory facts from functional analysis, fractional calculus theory, and measures of non-compactness which will be employed in the course of this manuscript.
Let \(\mathscr{L}(\mathbb{X})\) symbolize the Banach space of all bounded linear operators from \(\mathbb{X}\) into \(\mathbb{X}\), having norm \(\|\cdot \|_{\mathscr{L}(\mathbb{X})}\).
Let \(C(\mathscr{I},\mathbb{X})\) symbolize the space of all continuous functions from \(\mathscr{I}\) into \(\mathbb{X}\), having norm \(\|\cdot\|_{C(\mathscr {I},\mathbb{X})}\). Moreover, \(B_{r}(x,\mathbb{X})\) symbolizes the closed ball in \(\mathbb{X}\) with the middle at x and the distance r.
We recall that a measurable function \(x:\mathscr{I}\rightarrow \mathbb{X}\) is Bochner integrable iff \(\|x\|\) is Lebesgue integrable. (To get extra insights as regards the Bochner integral, refer to the treatise of Yosida [46].)
Permit \(L^{1}(\mathscr{I},\mathbb{X})\) signifies the Banach space of all measurable functions \(x:\mathscr{I}\rightarrow\mathbb{X}\) which are Bochner integrable and have the norm
Definition 2.1
([47], Definition 4)
Let \(\mathscr{A}: D\subseteq\mathbb{X}\rightarrow\mathbb{X}\) be a closed linear operator. The operator \(\mathscr{A}\) is considered to be sectorial if we can find \(0<\theta<\frac{\pi}{2}\), \(\mathcal{M}>0\), and \(\mu\in\mathbb{R}\) in such a way that the \(\rho(\mathscr{A})\) exists exterior of the segment
For short, we say that \(\mathscr{A}\) is sectorial of type \((\mathcal {M},\theta,\mu)\).
Let \(-\mathscr{A}\) signify the infinitesimal generator of an analytic semigroup in a Banach space and \(0\in\rho(\mathscr{A})\), where \(\rho(\mathscr {A})\) is the resolvent set of \(\mathscr{A}\). We characterize the fractional power \(\mathscr{A} ^{-q}\) by
We observe that \(\mathscr{A}^{q}=(\mathscr{A}^{-q})^{-1}\) is a closed linear operator with domain \(D(\mathscr{A}^{q})\supset D(\mathscr{A})\) is dense in \(\mathbb{X}\) for \(0< q\le1\). For an analytic semigroup \(\{\mathbb{T}(t)\}_{t\ge0}\), we have the accompanying theorem.
Theorem 2.1
([48], Theorem 6.13)
Let \(-\mathscr{A}\) be the infinitesimal generator of an analytic semigroup \(\{\mathbb{T}(t)\}_{t\ge0}\). If \(0\in\rho(\mathscr{A})\), at that point the accompanying features hold:
-
(a)
\(\mathbb{T}(t):\mathbb{X}\rightarrow D(\mathscr{A}^{q})\) for each \(t>0\) and \(q\ge0\).
-
(b)
For each \(x\in D(\mathscr{A}^{q})\), we keep \(\mathbb {T}(t)\mathscr{A}^{q}x=\mathscr{A}^{q}\mathbb{T}(t)x\).
-
(c)
For each \(t>0\), the operator \(\mathscr{A}^{q}\mathbb{T}(t)\) is bounded and \(\|\mathscr{A}^{q}\mathbb{T}(t)\|\le\mathcal{M}_{q}t^{-q}e^{-\delta t}\).
-
(d)
For \(0< a\le1\) and \(x\in D(\mathscr{A}^{q})\), we obtain \(\| \mathbb{T} (t)x-x\|\le C_{q}t^{q}\|\mathscr{A}^{q}x\|\).
To properly characterize our system, we claim that a function \(x:[\sigma,\tau]\rightarrow\mathbb{X}\) is a normalized piecewise continuous function on \([\sigma,\tau]\) if x is piecewise continuous and left continuous on \((\sigma,\tau]\). By the symbol \(\mathcal {PC}([\sigma,\tau]; \mathbb{X})\), we mean the space of normalized piecewise continuous functions from \([\sigma,\tau]\) into \(\mathbb{X}\). Specifically, we signify the space \(\mathcal{PC}\) established by all functions \(x:[0,T]\rightarrow\mathbb{X}\) in such a way that x is continuous at \(t\neq t_{i}\), \(x(t_{i}^{-})=x(t_{i})\) and \(x(t_{i}^{+})\) exists, for all \(i=1,2,\ldots,N\). It is not difficult to see that \(\mathcal{PC}\) is a Banach space having the norm \(\|x\|_{\mathcal{PC}}=\sup_{s\in [0,T]}\|x(s)\|\).
It needs to be outlined that, once the delay is infinite, then we should talk about the theoretical phase space \({\mathscr{B}}_{h}\) in a beneficial way. In this manuscript, we address phase spaces \({\mathscr {B}}_{h}\) which are the same as described in [49]. So, we bypass the details.
We expect that the phase space \(({\mathscr{B}}_{h},\|\cdot\|_{{\mathscr {B}}_{h}})\) is a semi-normed linear space of functions mapping \((-\infty ,0]\) into \(\mathbb{X}\), and fulfilling the subsequent elementary contexts as a result of Hale and Kato (see the case in point in [50, 51]).
If \(x:(-\infty,T]\rightarrow\mathbb{X}\), \(T>0\), is continuous on \(\mathscr{I}\) and \(x_{0}\in{\mathscr{B}}_{h}\), then for every \(t\in\mathscr{I}\) the accompanying conditions hold:
- (P1):
-
\(x_{t}\) is in \({\mathscr{B}}_{h}\).
- (P2):
-
\(\|x(t)\|_{\mathbb{X}}\le H\|x_{t}\|_{{\mathscr{B}}_{h}}\).
- (P3):
-
\(\|x_{t}\|_{{\mathscr{B}}_{h}}\le\mathscr{D}_{1}(t)\sup\{ \|x(s)\| _{\mathbb{X}}:0\le s\le t\}+\mathscr{D}_{2}(t)\|x_{0}\|_{{\mathscr {B}}_{h}}\), where \(H>0\) is a constant and \(\mathscr{D}_{1}(\cdot):[0,+\infty)\rightarrow [0,+\infty )\) is continuous, \(\mathscr{D}_{2}(\cdot):[0,+\infty)\rightarrow [0,+\infty )\) is locally bounded, and \(\mathscr{D}_{1}\), \(\mathscr{D}_{2}\) are independent of \(x(\cdot)\).
- (P4):
-
([27], p.430) The function \(t\rightarrow \varsigma_{t}\) is well described and continuous from the set
$$ \mathcal{R}\bigl(\varrho^{-}\bigr)=\bigl\{ \varrho(s,\psi):(s,\psi)\in[0,T]\times { \mathscr{B}}_{h}\bigr\} , $$into \({\mathscr{B}}_{h}\) and there is a continuous and bounded function \(J^{\varsigma}:\mathcal{R}(\varrho^{-})\rightarrow(0,\infty)\) to ensure that \(\| \varsigma_{t}\|_{{\mathscr{B}}_{h}}\le J^{\varsigma}(t)\|\varsigma\| _{{\mathscr{B}}_{h}}\) for every \(t\in\mathcal{R}(\varrho^{-})\).
Define the space
For the function \(\|\cdot\|_{\mathscr{B}_{T}}\) to be a seminorm in \(\mathscr{B}_{T}\), it is described by
Lemma 2.1
([52], Lemma 2.1)
Let \(x:(-\infty,T]\rightarrow\mathbb{X}\) be a function in such a way that \(x_{0}=\varsigma\), \(x|_{\mathscr{I}}\in\mathcal{PC}\) and if (P4) holds, then
where \(J^{\varsigma}=\sup_{t\in\mathcal{R}(\varrho^{-})}J^{\varsigma}(t)\), \(\mathscr{D}_{1}^{*}=\sup_{s\in[0,T]}\mathscr{D}_{1}(s)\), \(\mathscr{D}_{2}^{*}= \sup_{s\in[0,T]}\mathscr{D}_{2}(s)\).
Presently, we provide some fundamental definitions and outcomes of the fractional calculus theory that happen to be utilized additionally within this manuscript.
Definition 2.2
[3]
The fractional integral of order γ with the lower limit zero for a function f is determined as
where the right part is point-wise described on \([0,+\infty)\), where \(\Gamma(\cdot)\) is the gamma function.
Definition 2.3
[3]
The Riemann-Liouville derivative of order γ with the lower limit zero for a function \(f\in L^{1}(\mathscr {I},\mathbb{X})\) is characterized as
Definition 2.4
The Caputo derivative of order γ for a function \(f\in L^{1}(\mathscr{I},\mathbb{X})\) could be written
Definition 2.5
([53], Definition 4.59)
The generalized Mittag-Leffler special function \(E_{\alpha, \beta}\) is defined by
where \(\Upsilon_{0}\) is a contour which starts and ends at −∞ and encircles the disc \(|\lambda|\le|z|^{\frac{1}{\alpha}}\) counter-clockwise and C̃ denotes the complex plane. For short, set \(E_{\alpha}(z) = E_{\alpha,1}(z)\).
Definition 2.6
[53]
The Wright-type function is defined by
Therefore we have the following property [53], Property 4.60:
Presently, we are in a position to characterize the mild solution for the system (1.1)-(1.3). For this, first we consider the subsequent system
where \({}^{\mathrm{C}} D^{\alpha}_{t}\) and \(-\mathscr{A}\) are just like described in (1.1)-(1.3).
Now, we first consider the classical solutions to the problem (2.1)-(2.2). Then, based on the expression of such solutions, we define the mild solutions of the problem (2.1)-(2.2). Finally, the relations between the analytic semigroup \(\{\mathbb{T}(t)\}_{t\geq0}\) and some solution operators are obtained.
Lemma 2.2
([47], Lemma 6)
Using \(-\mathscr{A}\) to denote the infinitesimal generator of an analytic semigroup \(\{\mathbb{T}(t)\}_{t\geq0}\), then if \(\mathscr{F}\) satisfies a uniform Hölder condition with exponent \(\beta\in(0, 1]\), the solutions of the Cauchy system (2.1)-(2.2) are fixed points of the subsequent operator equation:
where
Here C is a suitable path satisfying \(\lambda^{\alpha}\notin\mu+ S_{\theta}\) for some \(\lambda\in C\).
Proof
According to the definitions of (2.2) and (2.3), we modify the Cauchy system (2.1)-(2.2) in the equivalent integral equation
Let \(\lambda>0\). Making use of the Laplace transform,
of (2.4), we obtain
Using \(\lambda^{\alpha}(\lambda^{\alpha} +\mathscr{A})^{-1} = I-\mathscr{A}(\lambda^{\alpha} +\mathscr{A})^{-1}\), the above equation is then inverse Laplace transformed to obtain
It is noted that \(\mathscr{F}\) satisfies a uniform Hölder condition with exponent \(\beta\in(0, 1)\). Hence, the classical solutions of Cauchy system (2.1)-(2.2) are fixed points of the operator equation
□
In view of Lemma 2.2, we determine the mild solutions of the system (2.1)-(2.2).
Definition 2.7
A function \(x:\mathscr{I}\rightarrow\mathbb{X}\) is considered to be a mild solution of problem (2.1)-(2.2) if \(x\in C(\mathscr{I}, \mathbb{X})\) fulfills the accompanying integral equation:
Remark 2.1
It is straightforward to confirm that the classical solution of the system (2.1)-(2.2) is a mild solution of the same system. Thus, Definition 2.7 is well defined (see [48, 54]).
Lemma 2.3
([47], Lemma 9)
Assuming \(-\mathscr{A}\) is the infinitesimal generator of an analytic semigroup, given by \(\{\mathbb{T}(t)\}_{t \geq0}\) and \(0 \in\rho (A)\), then we now have
Here \(\phi_{\alpha}(r)\) is the probability density function characterized on \((0, \infty)\) in such a way that its Laplace transform has the form
which fulfills
Proof
For all \(x \in D(\mathscr{A})\subset\mathbb{X}\), we have
Let
where \(\alpha\in(0, 1)\), \(\psi_{\alpha}(r) = \frac{1}{\pi}\sum_{1\leq n < \infty}(-1)^{n}r^{-\alpha n -1}\frac{\Gamma(n \alpha+ 1)}{n!}\sin(n\pi\alpha)\), and \(r \in(0, \infty)\) (see [55]). Thus, we obtain
where \(\phi_{\alpha}(r)= (\frac{1}{\alpha} )r^{-1-\frac {1}{\alpha}}\psi_{\alpha}(r^{\frac{-1}{\alpha}})\) is the probability density function outlined on \((0,\infty)\) in such a way that
It shows from (2.5) that
Then again, for all \(x\in D(\mathscr{A})\subset\mathbb{X}\), we notice that
Thus,
□
Before we characterize the mild solution for the system (1.1)-(1.3), finally, we treat the following system:
where \({}^{\mathrm{C}}D_{t}^{\alpha}\), \(g_{i}(t,x(t))\) and \(-\mathscr{A}\) are the same as defined in (1.1)-(1.3) and \(x_{0}\in\mathbb{X}\), \(\mathscr{F}\), \(\mathscr{G}\) are appropriate functions.
We notice that the impulses in problem (2.6)-(2.8) start abruptly at the points \(t_{i}\) and their action continues on the interval \([t_{i},s_{i}]\). More specifically, the function x takes an abrupt impulse at \(t_{i}\) and follows different rules in the two subintervals \((t_{i},s_{i}]\) and \((s_{i}, t_{i+1}]\) of the interval \((t_{i}, t_{i+1}]\). At the point \(s_{i}\), the function x is continuous.
By the results obtained in [24, 47, 56–59], we realize that the definition of mild solutions for fractional evolutions is more involved than integer order evolution equations. Furthermore, to construct the solutions for impulsive fractional differential equations, we need to effectively manage the fractional derivative and impulsive conditions due to the memory property of fractional calculus [53, 60, 61].
From the property of the Caputo derivative, the general solution of the system (2.6)-(2.8) can be composed as
where \(d_{i}\), \(i=1,2,\ldots,N\), are elements of \(\mathbb{X}\). From equation (2.9) and the function x being continuous at the points \(s_{i}\), we have, for \(i=1,2,\ldots, N\),
where \(d_{0}=x_{0}+\mathscr{G}(0,x_{0})\) and \(\chi_{[s_{i},t_{i+1})}\) is the characteristic function of \([s_{i}, t_{i+1})\). That is,
Presently, partly using [8, 56] and applying the Laplace transformation for (2.10) we get
where
At that point by the same calculations in [56] and the properties of the Laplace transform, we obtain
Here \(\mathbb{T}_{\alpha}\) and \(\mathbb{S}_{\alpha}\) are given by Lemma 2.3. Hence, we have
Presently the time has come to decide the estimations of \(d_{i}\), \(i=1,2,\ldots,N\). Utilizing the fact that x is continuous at the points \(s_{i}\), we get
Therefore, we obtain
Therefore, a mild solution of the model (2.6)-(2.8) is given by
where
Next, we show that this mild solution satisfy the system (2.6)-(2.8). To prove this, first we prove the following crucial lemma.
Lemma 2.4
Assuming \(-\mathscr{A}\) is the infinitesimal generator of an analytic semigroup, given by \(\{\mathbb{T}(t)\}_{t \geq0}\) and if \(0<\alpha <1\), then
and
where \(\mathbb{T}_{\alpha}(t)\) and \(\mathbb{S}_{\alpha}(t)\) are the same as defined in Lemma 2.2.
Proof
In perspective of \(\mathbb{T}_{\alpha}(t)\), we have
Therefore, we obtain
In view of (2.11) and (2.12), we have
In the same way, we have
and
Thus, it follows from (2.13) and (2.14) that
□
Now it is time to show that the mild solution satisfies the system (2.6)-(2.8). From the above discussion, we have
That is,
Taking the Caputo derivative on both sides and with regard of Lemma 2.4, we have
That is,
In a similar manner, we have
where
That is,
Taking the Caputo derivative on both sides and in view of Lemma 2.4, we obtain
That is,
From the above discussion, we observe that our definition of a mild solution satisfies the given system (2.6)-(2.8).
In accordance with the above discussion, now we present the mild solution for the system (1.1)-(1.3).
Definition 2.8
A function \(x : (-\infty,T]\rightarrow\mathbb{X}\) is called a mild solution of the model (1.1)-(1.3) if \(x_{0} = \varsigma\in{\mathscr{B}}_{h}\), \(x(\cdot)|_{\mathscr{I}}\in\mathcal{PC}\) and for each \(s \in[0, t)\) the function \(\mathscr{A}\mathbb{S}_{\alpha }(t - s)\mathscr{G}(s, x_{\varrho(s,x_{s})}) \) is integrable and
where
Before we complete this segment, finally, we demonstrate some long-recognizable results from the Hausdorff measure of non-compactness.
Now, we specify the Hausdorff measure of non-compactness \(\chi_{Y}\) being \(\chi_{Y}(B)= \inf\{\varepsilon> 0; B \text{ can be secured by a finite number of balls of radii smaller than } \varepsilon \text{ in } Y\}\), for a bounded set B in any Banach space Y.
In this manuscript, we designate by \(\chi_{C}\) the Hausdorff measure of non-compactness of \(C([0, T],\mathbb{X})\) and by \(\chi_{\mathcal {PC}}\) the Hausdorff measure of non-compactness of \(\mathcal{PC}\).
Now, we turn to the statement of the Darbo fixed point theorem.
Lemma 2.5
[1]
If \(\mathcal{W} \subseteq Y\) is closed and convex and \(0 \in\mathcal{W}\), the continuous map \(\Upsilon: \mathcal {W} \rightarrow\mathcal{W}\) is a \(\chi_{Y}\)-contraction, and if the set \(\{x\in\mathcal{W}: x=\lambda\Upsilon x\}\) is bounded for \(0 < \lambda < 1\), then the map ϒ has at least one fixed point in \(\mathcal{W}\).
Remark 2.2
For more details on this topic we suggest the reader to read [62], Definition 2.5, Lemmas 2.4, 2.8, and 2.9.
3 Existence results
In this segment, we show and demonstrate the existence of solutions for the model (1.1)-(1.3) under the Darbo [1] fixed point theorem together with Hausdorff measures of non-compactness.
Presently, we itemizing the subsequent suppositions:
-
(H1)
The function \(\mathscr{G}:\mathscr{I}\times{\mathscr {B}}_{h}\rightarrow \mathbb{X}\) is continuous and we can find constants \(\beta\in(0, 1)\), \(C_{1}>0\), and \(C_{2}>0\) in such a way that \(\mathscr{G}\) is \(\mathbb{X}_{\beta}\) -valued and fulfills the subsequent assumptions:
$$\begin{aligned}& \bigl\Vert (\mathscr{A})^{\beta}\mathscr{G}(t,\psi_{1})- ( \mathscr{A})^{\beta}\mathscr{G}(t,\psi_{2})\bigr\Vert _{\mathbb {X}}\leq C_{1}\Vert \psi_{1}- \psi_{2}\Vert _{{\mathscr{B}}_{h}}, \quad t\in\mathscr {I}, \psi_{1},\psi_{2}\in{\mathscr{B}}_{h}, \\& \bigl\Vert (\mathscr{A})^{\beta}\mathscr{G}(t,\psi )\bigr\Vert _{\mathbb{X} }\leq C_{1}\Vert \psi \Vert _{{\mathscr{B}}_{h}}+C_{2}, \quad t\in \mathscr{I} , \psi\in{\mathscr{B}}_{h}. \end{aligned}$$ -
(H2)
The function \(e:\mathscr{D}\times{\mathscr {B}}_{h}\rightarrow\mathbb{X}\) fulfills:
-
(i)
For every \((t,s)\in\mathscr{D}\), the function \(e(t,s,\cdot):{\mathscr{B}}_{h}\rightarrow\mathbb{X}\) is continuous and for each \(\psi\in{\mathscr{B}}_{h}\), the function \(e(\cdot,\cdot,\psi ):\mathscr{D}\rightarrow\mathbb{X}\) is strongly measurable.
-
(ii)
There exist a function \(m\in L^{1}(\mathscr{I},\mathbb {R}^{+})\) and a continuous non-decreasing function \(\Omega:\mathbb{R}^{+}\rightarrow (0,\infty)\) to ensure that
$$\bigl\Vert e(t,s,\psi)\bigr\Vert _{\mathbb{X}}\le m(s)\Omega\bigl(\Vert \psi \Vert _{{\mathscr {B}}_{h}}\bigr)\quad \text{for a.e. } t,s\in\mathscr{I}, \psi \in{\mathscr{B}}_{h}. $$ -
(iii)
There exists \(\mu\in L^{1}(\mathscr{I}\times\mathscr {I},\mathbb{R}^{+})\) to ensure that
$$\chi\bigl(e(t,s,H)\bigr)\le\mu(t,s) \Bigl[{\sup_{-\infty< \theta\le 0}}\chi \bigl( H(\theta)\bigr) \Bigr]\quad \text{for a.e. } t,s\in\mathscr{I}, \psi\in { \mathscr{B}}_{h}, $$where \(H(\theta)=\{v(\theta):v\in H\}\) and χ is the Hausdorff measures of non-compactness.
-
(i)
-
(H3)
The function \(\mathscr{F}:\mathscr{I}\times{\mathscr {B}}_{h}\times\mathbb{X} \rightarrow\mathbb{X}\) complies with the subsequent condition:
-
(i)
For a.e. \(t\in\mathscr{I}\), \((\psi,u)\rightarrow\mathscr {F}(t,\psi, u)\) is continuous and for all \((\psi,u)\in{\mathscr{B}}_{h}\times\mathbb {X}\), \(t\rightarrow\mathscr{F}(t,\psi, u)\) is strongly measurable.
-
(ii)
There exist a function \(\vartheta\in L^{1}(\mathscr {I},\mathbb{R}^{+})\) and a continuous non-decreasing function
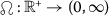 to ensure that
to ensure that
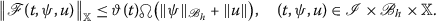
-
(iii)
For every bounded sets \(D\subset{\mathscr{B}}_{h}\), \(F\subset\mathbb{X}\), there exists a positive function \(\eta\in L^{1}(\mathscr{I},\mathbb{R} ^{+})\) in such a way that
$$\chi\bigl(\mathscr{F}(t,D,F)\bigr)\le\eta(t) \Bigl[{\sup_{-\infty< \theta\le 0} \chi\bigl(D(\theta)\bigr)+\chi(F)} \Bigr]\quad \text{for a.e. } t\in\mathscr{I}, $$where \(D(\theta)=\{w(\theta):w\in D\}\).
-
(i)
-
(H4)
The functions \(g_{i}: (t_{i}, s_{i}]\times{\mathscr {B}}_{h}\rightarrow\mathbb{X}\), \(i = 1,2,\ldots,N\), are continuous, and fulfill the subsequent conditions:
-
(i)
There exist constants \(c_{i}, \tilde{c}_{i}>0\), \(i = 1,2,\ldots,N\), in such a way that
$$ \bigl\Vert g_{i}(t,\psi)\bigr\Vert _{\mathbb{X}} \leq c_{i}\|\psi\|_{{\mathscr{B}}_{h}}+ \tilde {c}_{i}, \quad t \in(t_{i}, s_{i}],\psi\in {\mathscr{B}}_{h}. $$ -
(ii)
There exist constants \(\tilde{\mu}_{i}>0\) such that, for each bounded \(D\subset{\mathscr{B}}_{h}\),
$$ \chi\bigl( g_{i}(t,D)\bigr)\leq \tilde{\mu}_{i}\sup _{-\infty< \theta\leq0}\chi \bigl(D(\theta)\bigr) $$for a.e. \(t \in(t_{i}, s_{i}]\), \(i = 1, 2, \ldots,N\), where \(D(\theta)=\{u(\theta):u\in D\}\).
-
(i)
-
(H5)
For every bounded set \(\Lambda\subset{\mathscr{B}}_{h}\), the set \(\{t \rightarrow g_{i}(t, x_{\varrho(t,x_{t})}) : x_{\varrho(t,x_{t})} \in\Lambda\}\), \(i = 1,2,\ldots,N\), are equicontinuous in \({\mathscr{B}}_{h}\).
-
(H6)
The following inequalities hold:
$$\overline{\ell}=(\mathcal{M}+1) \biggl[ \biggl(\mathcal{M}_{0}+ \frac {\mathcal{M}_{1-\beta}\Gamma (\beta+ 1)}{\Gamma(\alpha\beta+ 1)}\frac{T^{\alpha\beta}}{\beta} \biggr)C_{1}\mathscr{D}_{1}^{*} \biggr]< 1 $$and
$$\Lambda_{0}=\max_{1\le i\le N}(\mathcal{M}+1) \biggl\{ \tilde{\mu }_{i}+\frac{\mathcal{M} (1+\mu^{*})T^{\alpha}}{\Gamma(\alpha+1)} \int_{0}^{T}\eta(s)\,ds \biggr\} < 1. $$
Remark 3.1
We represent \(\tilde{\mu}^{*}=\int_{0}^{s}\mu(s,\tau)\,d\tau<\infty\).
Theorem 3.1
Assume that (H1)-(H6) hold, and we expect that
\(\mu^{*}=1-\ell>0\), then the model (1.1)-(1.3) has at least one mild solution on
\(\mathscr{I}\), due to the fact
 and
and
Proof
We will transform the model (1.1)-(1.3) into a fixed-point problem. Let the operator \(\Upsilon:\mathscr{B}_{T}\rightarrow\mathscr{B}_{T}\) be specified by
with \(d_{i}\), \(i=1,2,3,\ldots,N\), defined by (2.16).
It is evident that the fixed points of the operator ϒ are mild solutions of the model (1.1)-(1.3). We express the function \(y(\cdot ):(-\infty,T]\rightarrow\mathbb{X}\) by
then \(y_{0}=\varsigma\). For every function \(z\in C(\mathscr{I},\mathbb {R})\) with \(z(0)=0\), we take z̅ characterized by
If \(x(\cdot)\) fulfills (2.15), we are able to split it as \(x(t)=y(t)+{z}(t)\), \(t\in\mathscr{I}\), which suggests \(x_{t}=y_{t}+{z}_{t}\), for each \(t\in\mathscr{I}\) and also the function \(z(\cdot)\) fulfills
where
Let \(\mathscr{B}_{T}^{0}=\{ z\in\mathscr{B}_{T}^{0}: z_{0}=0\in {\mathscr{B}}_{h}\}\). Let \(\|\cdot \|_{\mathscr{B}_{T}^{0}}\) be the seminorm in \(\mathscr{B}_{T}^{0}\) described by
as a result \((\mathscr{B}_{T}^{0}, \|\cdot\|_{\mathscr{B}_{T}^{0}})\) is a Banach space. We delimit the operator \(\overline{\Upsilon}:\mathscr{B}_{T}^{0}\rightarrow \mathscr{B}_{T}^{0}\) by
with \(\tilde{d}_{i}\), \(i=1,2,\ldots,N\), defined by (3.2).
Thus, the operator ϒ has a fixed point if and only if ϒ̅ has a fixed point.
Remark 3.2
From the above discussion, we have the subsequent estimates:
(i) For \(\lambda\in(0,1)\), then
where \(\|z^{\lambda}\|_{t}=\sup_{0\le s\le t}\|z^{\lambda}(s)\|_{\mathbb{X} }\) and \(c_{n}=(\mathscr{D}_{2}^{*}+J^{\varsigma}+\mathscr {D}_{1}^{*}\mathcal{M}H)\|\varsigma\| _{{\mathscr{B}}_{h}}\).
(ii) In the perspective of Theorem 2.1 and for any \(x\in \mathbb{X}\) and \(\beta\in(0,1)\), we have
On the other hand, from \(\int_{0}^{\infty}r^{-q}\psi_{\alpha}(r)\,dr=\frac{\Gamma(1+\frac{q}{\alpha})}{\Gamma(1+q)}\), for all \(q\in [0,1]\) (see [56], Lemma 3.2), we have
Then, by (3.3) and (3.4), it is easy to see that
It is obvious that the function \(\theta\rightarrow\mathscr {A}\mathbb{T}_{\alpha}(t-\theta)\mathscr{G}(\theta,x_{\varrho(\theta,x_{\theta})})\) is integrable on \([0,t)\) for every \(t>0\).
(iii) In view of [56], Lemma 3.2, (3.5), and (H1), we have
where \(\mathcal{M}_{0}=\|(\mathscr{A})^{-\beta}\|\), and
(iv) From the assumption (H4) with the above discussion, we get
(v) In perspective of the suppositions (H2)-(H3) and (3.4), we obtain

(vi)
(vii)
(viii) Now, we define \((\overline{\Upsilon}_{1} z)(t)\) as
Presently, we obtain
Since
we have
and
Now, we enter the main proof of this theorem. Presently, let us demonstrate that ϒ̅ has a fixed point. For greater comprehensibility, we divide the treatment into a few steps.
Step 1: To use Lemma 2.2, we set up a priori estimates for the solutions of the integral equation \(z=\lambda\overline {\Upsilon}z\), \(\lambda \in(0,1)\). Let \(z^{\lambda}\) be a solution of \(z=\lambda\overline {\Upsilon}z\), \(\lambda\in(0,1)\), \(z\in\mathcal{PC}\). From the assumptions (H1)-(H4) together with the Remark 3.2, we obtain, for \(t\in[0,t_{1}]\),

For any \(t\in(t_{i},s_{i}]\), \(i=1,2,\ldots,N\), we have
In the same way, for any \(t\in(s_{i},t_{i+1}]\), \(i=1,2,\ldots,N\), we obtain

Then, for all \(t\in\mathscr{I}\), we find that

where
Thus

From (3.1), we realize that
Hence

We conceive the function β characterized by
Because of the aforementioned inequality, we maintain, for \(t\in \mathscr{I}\),

Let us refer to the right-hand part of the overhead inequality as \(v^{\lambda}(t)\). Then we keep \(\beta^{\lambda}(t)\le v^{\lambda}(t)\) for all \(t\in\mathscr{I}\). Then we obtain
This leads us to the accompanying inequality for \(t\in\mathscr{I}\),

where

Next, we weight the function
Then we produce \(\eta^{\lambda}(0)=v^{\lambda}(0)\) and \(v^{\lambda}(t)\le\eta^{\lambda}(t)\) for all \(t\in\mathscr{I}\). Applying the non-decreasing character of  , we obtain
, we obtain

We characterize the function \(\tilde{m}(t)=\max \{\frac {\mathscr{D} _{1}^{*}\mathcal{M}(\mathcal{M}+1){T^{\alpha}}}{\mu^{*}\Gamma(\alpha +1)}\vartheta(t), m(t) \}\), \(t\in\mathscr{I}\), which suggests that

and hence

which indicates that the set of functions \(\{\eta^{\lambda}(\cdot ):\lambda\in(0,1)\}\) is bounded on \(\mathscr{I}\). This reveals that the set \(\{z^{\lambda}(\cdot): \lambda\in(0,1)\}\) is bounded on \(\mathscr{I}\).
Step 2: Now, we demonstrate that \(\overline{\Upsilon }:\mathscr{B}_{T}^{0} \rightarrow\mathscr{B}_{T}^{0}\) is continuous.
Let \(\{z^{(n)}\}_{n=0}^{\infty}\subseteq\mathscr{B}_{T}^{0}\) with \(z^{(n)}\rightarrow z\) in \(\mathscr{B}_{T}^{0}\). Then we can find a number \(q > 0\) in such a way that \(\| z^{(n)}(t)\|\leq q\) for all n and a.e. \(t \in\mathscr{I}\), so \(z^{(n)} \in B_{q}=\{z\in\mathscr{B}_{T}^{0}: \|z\|_{\mathscr {B}_{T}^{0}}\le q\}\subseteq\mathscr{B}_{T}^{0}\) and \(z \in B_{q}\). From Remark 3.2, we have \(\|z_{\varrho (t,z^{n}_{t}+y_{t})}^{(n)}+y_{\varrho(t,z^{n}_{t}+y_{t})}\|_{{\mathscr{B}}_{h}}\le q^{\prime}\), \(t\in\mathscr{I}\). By (H2), we obtain
for every \(t\in\mathscr{I}\), and considering the fact that

By (H2), (H3), Remark 3.2(vi)-(vii), and the dominated convergence theorem, we obtain, for \(t\in[0,t_{1}]\),
For any \(t \in(t_{i}, s_{i} ]\), \(i = 1,2,\ldots,N\), we obtain
In the same way, for any \(t\in(s_{i}, t_{i+1}]\), \(i=1,2,\ldots,N\), we have
It is simple to see that
Thus, ϒ̅ is continuous.
Step 3: ϒ̅ is χ-contraction.
To demonstrate this, we split ϒ̅ as \(\overline {\Upsilon}_{1}+\overline{\Upsilon}_{2}\) for \(t\in\mathscr{I} \), where \((\overline{\Upsilon}_{1} z)(t)\) is defined in Remark 3.2(viii) and
First, we show that \(\overline{\Upsilon}_{1}\) is Lipschitz continuous on \(\mathscr{B}_{T}^{0}\). In fact \(z,\overline{z}\in\mathscr{B}_{T}^{0}\), then from Remark 3.2(viii), we have, for all \(t\in[0,t_{1}]\),
In the same way, for any \(t\in(s_{i}, t_{i+1}]\), \(i=1,2,\ldots,N\), we obtain
Then, for all \(t\in\mathscr{I}\), we get
From the assumption (H6), we observe that \(\overline{\ell}<1\). Hence, \(\overline{\Upsilon} _{1}\) is Lipschitz continuous.
Next, we prove that \(\overline{\Upsilon}_{2}\) maps bounded sets into equicontinuous sets of \(\mathscr{B}_{T}^{0}\).
Let \(0 < \eta_{1} < \eta_{2} \leq t_{1}\). For each \(z\in B_{q}\), we have

For any \(\eta_{1}, \eta_{2} \in(t_{i}, s_{i} ]\), \(\eta_{1} < \eta_{2}\), \(i = 1,2,\ldots,N\), we have
In the same way, for any \(\eta_{1}, \eta_{2} \in(s_{i}, t_{i+1}]\), \(\eta_{1} < \eta_{2}\), \(i = 1, 2,\ldots,N\), we get

At the point when \(\eta_{2}\rightarrow\eta_{1}\), the right-hand side of the overhead inequality has a tendency to zero, subsequently by (H4)-(H5), \(\mathbb{T}_{\alpha}(t)\), \(\mathbb{S}_{\alpha}(t)\) are uniformly continuous, this demonstrates the equicontinuity.
We finish this step by proving that \(\overline{\Upsilon}_{2}\) is a χ-contraction.
For any \(\mathcal{W}\subset\mathscr{B}_{T}^{0}\), \(\mathcal{W}\) is piecewise equicontinuous since \(\mathbb{S}_{\alpha}(t)\) is equicontinuous. Hence, from the fact that \(\varrho(s,z_{s}+y_{s})\le s\), \(s\in\mathscr{I}\) and [62], Lemmas 2.8 and 2.9 and \(\chi_{\mathcal{PC}}=\sup\{\chi(\mathcal{W}(t)), t\in[s_{i}, t_{i+1}]\}\), \(i=0,1,2,\ldots,N\). Then, for each bounded set \(\mathcal{W}\in\mathcal{PC}\), from the assumptions (H2)-(H4), we have, for \(t\in[0,t_{1}]\),
For any \(t\in(t_{i},s_{i}]\), \(i=1,2,\ldots,N\), we have
In the same way, for any \(t\in(s_{i}, t_{i+1}]\), \(i=1,2,\ldots,N\), we have
Along these lines, for all \(t \in\mathscr{I}\), we get
and
where \(\Lambda_{0}=\max_{1\le i\le N}(\mathcal{M}+1) (\tilde{\mu}_{i}+ \frac{\mathcal{M}(1+\tilde{\mu}^{*}_{i})T^{\alpha}}{\Gamma (\alpha+1)}\int _{0}^{T}\eta(s)\,ds )<1\). Therefore ϒ̅ is χ-contraction. In the perspective of Lemma 2.5, we realize that ϒ̅ has at least one fixed point \(z^{*}\in\mathcal{W}\subset\mathscr{B}_{T}^{0}\). Let \(x(t)=z^{*}(t)+y(t)\) on \((-\infty,T]\). Along these lines, x is a fixed point of the operator ϒ which is the mild solution of the system (1.1)-(1.3). Thus, the confirmation is finished. □
4 Applications
Below, we illustrate by two examples our theoretical results.
Example 1
First, we treat the IFNIDE with SDD and NII of the model
where \({}^{\mathrm{C}}D_{t}^{q}\) is Caputo’s fractional derivative of order \(0< q<1\), \(0=t_{0}=s_{0}< t_{1}< t_{2}<\cdots<t_{N-1}\le S_{N}\le t_{N}\le t_{N+1}=T\) are pre-fixed real numbers and \(\varsigma\in{{\mathscr{B}}_{h}}\). We consider \(\mathbb{X}=L^{2}[0,\pi]\) having the norm \(\|\cdot\|_{L^{2}}\) and determine the operator \(\mathscr{A}:D(\mathscr{A})\subset\mathbb{X}\rightarrow \mathbb{X}\) by \(\mathscr{A}w=w^{\prime\prime}\) having the domain
Then
where \(w_{n}(s)=\sqrt{\frac{2}{\pi}}\sin(ns)\), \(n=1,2,\ldots\) , denotes the orthogonal set of eigenvectors of \(\mathscr{A}\). It has long been well known that \(\mathscr{A}\) is the infinitesimal generator of an analytic semigroup \(\{\mathbb{T}(t)\}_{t\ge0}\) in \(\mathbb{X}\) and is provided by
We can find a constant \(\mathcal{M}> 0\) in such a way that \(\|\mathbb{T}(t)\|\leq\mathcal {M}\). If we fix \(\beta= \frac{3}{4}\), then the operator \((-\mathscr{A})^{\frac{3}{4}}\) is given by
in which \((D(-A)^{\frac{3}{4}}) = \{ \omega(\cdot) \in\mathbb{X}: \sum_{n=1 }^{\infty} n^{\frac{8}{3}}\langle\omega,w_{n}\rangle w_{n}\in \mathbb{X} \}\). Then
For the phase space, we choose \(h=e^{2s}\), \(s<0\), then \(l=\int _{-\infty}^{0}h(s)\,ds=\frac{1}{2}<\infty\), for \(t \le0\), and we determine
Hence, for \((t,\varsigma)\in[0,b]\times{\mathscr{B}}_{h}\), where \(\varsigma (\theta)(x)=\varsigma(\theta,x)\), \((\theta,x)\in(-\infty,0]\times [0,\pi]\). Set
we have
where
Here, we believe that:
-
(i)
the functions \(\varrho_{i}:[0,\infty)\rightarrow[0,\infty )\), \(i=1,2\) are continuous;
-
(ii)
the functions \(\mu_{i}(t,x,\theta)\) are continuous in \([0,T]\times[0,\pi]\times(-\infty,0]\), \(i=1,2\);
-
(iii)
the function \(k(t-s)\) is continuous in \([0,T]\) and \(k(t-s)\ge0\);
-
(iv)
the functions \(\tilde{\mu}_{i}\in C([0,\infty ),\mathbb{R})\), \(i=1,2,\ldots,N\), are continuous and bounded. Moreover, \(\mathscr {G}(t,\cdot)\), \(g_{i}\), \(i=1,2,\ldots,N\) are bounded linear operators.
Correspondingly, the aforementioned model (4.1)-(4.4) can be written in the theoretical form as model (1.1)-(1.3). Additionally, we can force some acceptable circumstances on the above characterized functions to check the presumptions of Theorem 3.1. As a result, from Theorem 3.1, the model (4.1)-(4.4) has a mild solution on \([0,T]\).
Example 2
Now, we consider the IFNIDE with SDD and NII of the model
where \({}^{\mathrm{C}}D_{t}^{q}\) is the same as defined in Example 1. In the perspective of this example, we set
where
then, with these settings, equations (4.5)-(4.8) can be written in the theoretical form of model (1.1)-(1.3).
To treat this system we assume that \(\varrho_{i}:[0,\infty)\rightarrow [0,\infty)\), \(i=1,2\), are continuous. Now, we can see that, for \(t\in [0,\pi]\), \(\varsigma, \overline{\varsigma}\in{\mathscr{B}}_{h}\), we have
where \(C_{\varsigma}=\frac{\sqrt{\pi}}{49}\) and
Similarly, we conclude
where \(L_{\mathscr{F}}=\frac{34\sqrt{\pi}}{225}\) and
we can see that each bounded set \(D\subset{\mathscr{B}}_{h}\), \(F\subset \mathbb{X}\),
Moreover, we have for any \(t\in(t_{i},s_{i}]\), \(i=1,2,\ldots,N\),
where \(c_{g_{i}}=\frac{\sqrt{\pi}}{36}\), and also, we can see that, for each bounded set \(D\subset{\mathscr{B}}_{h}\),
where \(\tilde{c}_{g_{i}}=\max\{c_{g_{i}}\}\), \(i=1,2,\ldots,N\).
Therefore, (H1), (H3), (H4) are all satisfied and  , \(\int_{1}^{+\infty}\frac{ds}{s}=+\infty\). Then, by using Theorem 3.1, we deduce the following result.
, \(\int_{1}^{+\infty}\frac{ds}{s}=+\infty\). Then, by using Theorem 3.1, we deduce the following result.
Proposition 4.1
Under the above assumptions, if \(\Lambda_{0}=\max_{1\le i\le N}(\mathcal{M}+1) \{\tilde{c}_{g_{i}}+\frac{\mathcal {M}(1+\mu^{*})}{\Gamma(\alpha +1)} L_{\mathscr{F}} \}<1\), \(\overline{\ell }=(\mathcal{M}+1) [\mathcal{M}_{0}+\frac {M_{\frac{1}{4}}\Gamma(\frac{3}{4}+1)}{\frac{3}{4}\Gamma(\frac {3}{4}+1)}C_{\varsigma}\mathscr{D}_{1}^{*} ]<1\), with \(\mu^{*}=1\), \(\mathcal{M}_{0}=\|(\mathscr{A} )^{-\frac{3}{4}}\|\), and
then the system (4.5)-(4.8) admits a mild solution on \([0,1]\).
References
Banas, J, Goebel, K: Measure of Noncompactness in Banach Space. Lecture Notes in Pure and Applied Mathematics. Dekker, New York (1980)
Baleanu, D, Machado, JAT, Luo, ACJ: Fractional Dynamics and Control. Springer, New York (2012)
Kilbas, A, Srivastava, H, Trujillo, JJ: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Agarwal, RP, Ahmad, B, Alsaedi, A, Shahzad, N: Dimension of the solution set for fractional differential inclusions. J. Nonlinear Convex Anal. 14(2), 319-329 (2013)
Agarwal, RP, Ahmad, B, Alsaedi, A, Shahzad, N: Existence and dimension of the set of mild solutions to semilinear fractional differential inclusions. Adv. Differ. Equ. 2012, 74 (2012)
Agarwal, RP, Ahmad, B: Existence of solutions for impulsive anti-periodic boundary value problems of fractional semilinear evolution equations. Dyn. Contin. Discrete Impuls. Syst., Ser. A Math. Anal. 18, 457-470 (2011)
Li, H-L, Jiang, Y-L, Wang, Z, Zhang, L, Teng, Z: Global Mittag-Leffler stability of coupled system of fractional-order differential equations on network. Appl. Math. Comput. 270(1), 269-277 (2015)
Shu, XB, Xu, F, Shi, Y: S-Asymptotically ω-positive periodic solutions for a class of neutral fractional differential equations. Appl. Math. Comput. 270(1), 768-776 (2015)
Yi, M, Wang, L, Jun, H: Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel. Appl. Math. Model. (2015). doi:10.1016/j.apm.2015.10.009
Ren, J, Sun, Z, Dai, W: New approximations for solving the Caputo-type fractional partial differential equations. Appl. Math. Model. (2015). doi:10.1016/j.apm.2015.10.011
Wang, JR, Zhang, Y: Nonlocal initial value problems for differential equations with Hilfer fractional derivative. Appl. Math. Comput. 266(1), 850-859 (2015)
Zhao, K: Impulsive boundary value problems for two classes of fractional differential equation with two different Caputo fractional derivatives. Mediterr. J. Math. (2015). doi:10.1007/s00009-015-0536-0
Abbas, MI: Ulam stability of fractional impulsive differential equations with Riemann-Liouville integral boundary conditions. J. Contemp. Math. Anal. 50(5), 209-219 (2015)
Bonanno, G, Rodriguez-Lopez, R, Tersian, S: Existence of solutions to boundary value problem for impulsive fractional differential equations. Fract. Calc. Appl. Anal. 17(3), 717-744 (2014)
Rodriguez-Lopez, R, Tersian, S: Multiple solutions to boundary value problem for impulsive fractional differential equations. Fract. Calc. Appl. Anal. 17(4), 1016-1038 (2014)
Lv, Z, Chen, B: Existence and uniqueness of positive solutions for a fractional switched system. Abstr. Appl. Anal. 2014, Article ID 828721 (2014)
Podlubny, I: Fractional Differential Equations. Academic Press, New York (1999)
Guendouzi, T, Benzatout, O: Existence of mild solutions for impulsive fractional stochastic differential inclusions with state-dependent delay. Chin. J. Math. 2014, Article ID 981714 (2014)
Qin, H, Zuo, X, Liu, J: Existence and controllability results for fractional impulsive integrodifferential systems in Banach spaces. Abstr. Appl. Anal. 2013, Article ID 295837 (2013)
Chang, Y-K, Nieto, JJ, Zhao, Z-H: Existence results for a nondensely-defined impulsive neutral differential equation with state-dependent delay. Nonlinear Anal. Hybrid Syst. 4(3), 593-599 (2010)
Agarwal, RP, Andrade, BD, Siracusa, G: On fractional integro-differential equations with state-dependent delay. Comput. Math. Appl. 62(3), 1143-1149 (2011)
Benchohra, M, Berhoun, F: Impulsive fractional differential equations with state-dependent delay. Commun. Appl. Anal. 14(2), 213-224 (2010)
Aissani, K, Benchohra, M: Fractional integro-differential equations with state-dependent delay. Adv. Dyn. Syst. Appl. 9(1), 17-30 (2014)
Carvalho dos Santos, JP, Mallika Arjunan, M, Cuevas, C: Existence results for fractional neutral integrodifferential equations with state-dependent delay. Comput. Math. Appl. 62(3), 1275-1283 (2011)
Dabas, J, Gautam, GR: Impulsive neutral fractional integro-differential equation with state-dependent delay and integral boundary condition. Electron. J. Differ. Equ. 2013, 273 (2013)
Gautam, GR, Dabas, J: Existence result of fractional functional integrodifferential equation with not instantaneous impulse. Int. J. Adv. Appl. Math. Mech. 1(3), 11-21 (2014)
Gautam, GR, Dabas, J: Mild solution for fractional functional integro-differential equation with not instantaneous impulse. Malaya J. Mat. 2(3), 428-437 (2014)
Pandey, DN, Das, S, Sukavanam, N: Existence of solution for a second-order neutral differential equation with state dependent delay and non-instantaneous impulses. Int. J. Nonlinear Sci. 18(2), 145-155 (2014)
Das, S, Pandey, DN, Sukavanam, N: Existence of solution and approximate controllability for neutral differential equation with state dependent delay. Int. J. Partial Differ. Equ. 2014, Article ID 787092 (2014)
Lakshmikantham, V, Bainov, DD, Simeonov, PS: Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Stamova, IM: Stability Analysis of Impulsive Functional Differential Equations. de Gruyter, Berlin (2009)
Graef, JR, Henderson, J, Ouahab, A: Impulsive Differential Inclusions: A Fixed Point Approach. de Gruyter, Berlin (2013)
Bainov, D, Covachev, V: Impulsive Differential Equations with a Small Parameter. World Scientific, Singapore (1995)
Benchohra, M, Henderson, J, Ntouyas, SK: Impulsive Differential Equations and Inclusions. Contemporary Mathematics and Its Applications, vol. 2. Hindawi Publishing Corporation, New York (2006)
Hernandez, E, Anguraj, A, Mallika Arjunan, M: Existence results for an impulsive second order differential equation with state-dependent delay. Dyn. Contin. Discrete Impuls. Syst., Ser. A Math. Anal. 17, 287-301 (2010)
Hernandez, E, O’Regan, D: On a new class of abstract impulsive differential equations. Proc. Am. Math. Soc. 141(5), 1641-1649 (2013)
Pierri, M, O’Regan, D, Rolnik, V: Existence of solutions for semi-linear abstract differential equations with not instantaneous impulses. Appl. Math. Comput. 219(12), 6743-6749 (2013)
Suganya, S, Mallika Arjunan, M, Trujillo, JJ: Existence results for an impulsive fractional integro-differential equation with state-dependent delay. Appl. Math. Comput. 266(1), 54-69 (2015)
Arthi, G, Park, JH, Jung, HY: Existence and exponential stability for neutral stochastic integrodifferential equations with impulses driven by a fractional Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 32, 145-157 (2016)
Yukunthorn, W, Ahmad, B, Ntouyas, SK, Tariboon, J: On Caputo-Hadamard type fractional impulsive hybrid systems with nonlinear fractional integral conditions. Nonlinear Anal. Hybrid Syst. 19, 77-92 (2016)
Zhang, L, Liang, Y: Monotone iterative technique for impulsive fractional evolution equations with noncompact semigroup. Adv. Differ. Equ. 2015, 324 (2015)
Zhang, Y, Wang, JR: Nonlocal Cauchy problems for a class of implicit impulsive fractional relaxation differential systems. J. Appl. Math. Comput. (2015). doi:10.1007/s12190-015-0943-1
Diop, MA, Rathinasamy, S, Ndiaye, AA: Neutral stochastic integrodifferential equations driven by a fractional Brownian motion with impulsive effects and time-varying delays. Mediterr. J. Math. (2015). doi:10.1007/s00009-015-0632-1
Rajivganthi, C, Thiagu, K, Muthukumar, P, Balasubramaniam, P: Existence of solutions and approximate controllability of impulsive fractional stochastic differential systems with infinite delay and Poisson jumps. Appl. Math. 60(4), 395-419 (2015)
Kumar, P, Pandey, DN, Bahuguna, D: On a new class of abstract impulsive functional differential equations of fractional order. J. Nonlinear Sci. Appl. 7, 102-114 (2014)
Yosida, K: Functional Analysis, 6th edn. Springer, Berlin (1980)
Shu, XB, Xu, F: The existence of solutions for impulsive fractional partial neutral differential equations. J. Math. 2013, Article ID 147193 (2013)
Pazy, A: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, New York (1983)
Dabas, J, Chauhan, A: Existence and uniqueness of mild solution for an impulsive fractional integro-differential equation with infinite delay. Math. Comput. Model. 57(3-4), 754-763 (2013)
Hale, J, Kato, J: Phase space for retarded equations with infinite delay. Funkc. Ekvacioj 21, 11-41 (1978)
Hino, Y, Murakami, S, Naito, T: Functional Differential Equations with Unbounded Delay. Springer, Berlin (1991)
Fu, X, Huang, R: Existence of solutions for neutral integro-differential equations with state-dependent delay. Appl. Math. Comput. 224, 743-759 (2013)
Zhou, Y: Basic Theory of Fractional Differential Equations. World Scientific, Singapore (2014)
Lunardi, A: Analytic Semigroups and Optimal Regularity in Parabolic Problems. Birkhäuser, Basel (1995)
Mainardi, F, Paradisi, P, Gorenflo, R: Probability distributions generated by fractional diffusion equations. In: Kertesz, J, Kondor, I (eds.) Econophysics: An Emerging Science. Kluwer Academic, Dordrecht (2000)
Zhou, Y, Jiao, F: Existence of mild solutions for fractional neutral evolution equations. Comput. Math. Appl. 59(3), 1063-1077 (2010)
Shu, XB, Lai, Y, Chen, Y: The existence of mild solutions for impulsive fractional partial differential equations. Nonlinear Anal., Theory Methods Appl. 74(5), 2003-2011 (2011)
Shu, XB, Wang, Q: The existence and uniqueness of mild solutions for fractional differential equations with nonlocal conditions of order \(1<\alpha<2\). Comput. Math. Appl. 64, 2100-2110 (2012)
Wang, X, Shu, XB: The existence of positive mild solutions for fractional differential evolution equations with nonlocal conditions of order \(1<\alpha<2\). Adv. Differ. Equ. 2015, 159 (2015)
Fu, X, Liu, X, Lu, B: On a new class of impulsive fractional evolution equations. Adv. Differ. Equ. 2015, 227 (2015)
Shu, XB, Shi, Y: A study on the mild solution of impulsive fractional evolution equations. Appl. Math. Comput. 273, 465-476 (2016)
Ye, R: Existence of solutions for impulsive partial neutral functional differential equation with infinite delay. Nonlinear Anal. 73(1), 155-162 (2010)
Acknowledgements
The authors are grateful to the anonymous referees for their constructive comments and helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors have made equal contributions. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Suganya, S., Baleanu, D., Kalamani, P. et al. On fractional neutral integro-differential systems with state-dependent delay and non-instantaneous impulses. Adv Differ Equ 2015, 372 (2015). https://doi.org/10.1186/s13662-015-0709-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0709-y
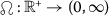 to ensure that
to ensure that