- Research Article
- Open access
- Published:
A study of nonlocal problems of impulsive integrodifferential equations with measure of noncompactness
Advances in Difference Equations volume 2013, Article number: 205 (2013)
Abstract
In this paper, we show the existence of mild solutions to a nonlocal problem of impulsive integrodifferential equations via a measure of noncompactness in a Banach space. Our work is based on a new fixed point theorem and it generalizes some existing results on the topic in the sense that we do not require the semigroup and nonlinearity involved in the problem to be compact.
1 Introduction
In this paper, we discuss the existence of solutions for the following nonlocal problem of integrodifferential equations:
where A generates a -semigroup , , in a Banach space X, , , , , with , , , and with , representing the right and left limit of u at , respectively. Here = { is continuous at , left continuous at , and the right-hand limit exists for }. Notice that the set equipped with the norm is a Banach space.
Integrodifferential equations arise in the mathematical modeling of several natural phenomena and various investigations led to the exploration of their different aspects. The theory of semigroups of bounded linear operators is closely related to the solution of differential and integrodifferential equations in Banach spaces. In recent years, this theory has been applied to a large class of nonlinear differential equations in Banach spaces. Based on the method of semigroups, the existence and uniqueness of mild, strong and classical solutions of semilinear evolution equations were discussed by Pazy [1]. For further details, see [2–5] and the references cited therein.
The theory of impulsive differential equations is an important branch of differential equations and has an extensive physical background. Impulsive differential equations help modeling many physical systems whose states are subject to abrupt changes at certain moments. Examples include population biology, the diffusion of chemicals, the spread of heat, the radiation of electromagnetic waves, etc. [6–9]. Dynamical systems with impulsive effects have been an object of intensive investigations [10–12]. The study of semilinear nonlocal initial problem was initiated by Byszewski [13, 14] and the importance of the problem lies in the fact that it is more general and yields better effect than the classical initial conditions. Therefore, it has been extensively studied under various conditions on the operator A and the nonlinearity f by several authors [15–17].
Byszewski and Lakshmikantham [18] showed the existence and uniqueness of mild solutions and classical solutions when f and g in (1.1) satisfy Lipschitz type conditions. Ntouyas and Tsamotas [19, 20] studied the case of compact-valued f and T. Zhu et al. [21] discussed the existence of mild solutions for abstract semilinear evolution equations in Banach spaces. In [11], the author discussed the existence and uniqueness of mild and classical solutions for the impulsive semilinear differential evolution equation. In [22], Agarwal et al. studied the existence and dimension of the set of mild solutions to semilinear fractional differential inclusions. Lizama and Pozo [23] investigated the existence of mild solutions for semilinear integrodifferential equation with nonlocal initial conditions by using Hausdorff measure of noncompactness via a fixed-point. In a recent paper [24], the authors studied the existence of mild solutions to an impulsive differential equation with nonlocal conditions by applying Darbo-Sadovskii’s fixed point theorem. For some more recent results and details, see [25–37].
Motivated by [23], in this paper we aim to establish some existence results for mild solutions of (1.1) without demanding the compactness condition on T and f. In this scenario, our work extends and improves some results obtained in [38, 39]. In Section 2, we recall some definitions and facts about semigroup T and the measure of noncompactness, while Section 3 deals with the existence of mild solutions for (1.1).
2 Preliminary result
Let denote the space of X-valued Bochner functions on with the norm defined by . A -semigroup is said to be compact if is compact for any . If the semigroup is compact, then are equicontinuous at all with respect to u in all bounded subset of X, that is, the semigroup is equicontinuous.
In this paper, α denotes the Hausdorff measure of noncompactness on both X and . The following lemma describes some properties of the Hausdorff measure of noncompactness.
Lemma 2.1 [40]
Let and denote Hausdorff measures of noncompactness on the real Banach spaces 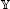 and ℤ, respectively, and be bounded. Then
and ℤ, respectively, and be bounded. Then
-
1.
B is pre-compact if and only if ;
-
2.
, where and convB mean the closure and convex hull of B, respectively;
-
3.
, where ;
-
4.
, where ;
-
5.
;
-
6.
for any ;
-
7.
If the map is Lipschitz continuous with constant k, then for any bounded subset ;
-
8.
, where means the nonsymmetric (or symmetric) Hausdorff distance between B and C in
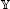 ;
; -
9.
If is a decreasing sequence of bounded closed nonempty subsets of
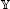 and , then is nonempty and compact in
and , then is nonempty and compact in 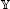 .
.
The map is said to be a -contraction if there exists a constant such that for any bounded closed subset , where 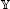 is a Banach space.
is a Banach space.
In the sequel, we need the following known results.
Lemma 2.2 [40]
If is bounded, then for all , where . Furthermore, if W is equicontinuous on , then is continuous on , and .
Lemma 2.3 [41]
If is uniformly integrable, then is measurable and
Lemma 2.4 [39]
If the semigroup is equicontinuous and there exists , then the set
is equicontinuous on .
Lemma 2.5 [42]
If W is bounded, then for each , there is a sequence such that .
Lemma 2.6 [43]
Suppose that , and let
Then (), where is an arbitrary real number and are binomial coefficients [44].
Lemma 2.7 ([45] Fixed point theorem)
Let Q be a closed and convex subset of a real Banach space X, let be a continuous operator and be bounded. For each bounded subset , set
If there exist a constant and a positive integer such that for each bounded subset , , then A has a fixed point in Q.
Definition 2.8 A function is called a mild solution of system (1.1) if and satisfies the following equation:
3 Existence result
In this section, we show the existence of solutions for problem (1.1) by applying Lemma 2.7.
For some real constants r and w, we define
For the forthcoming analysis, we need the following assumptions:
() The semigroup generated by A is equicontinuous and ;
() is such that there exist positive constants c and d such that , for all ;
() is of Caratheódory type, that is, is measurable for all , and is continuous for a.e. ;
() there exist a function and a nondecreasing continuous function such that for all a.e. ;
() there exist such that for any bounded sets ,
for a.e. ;
() The functions , , are completely continuous and uniformly bounded, and ;
() there exists a positive constant γ such that
where N, c, d, Ω, Λ are given by assumptions (), (), (), ().
In passing, we remark that
-
(i)
If A is the generator of an analytic semigroup or a differentiable semigroup , then is an equicontinuous -semigroup [1].
-
(ii)
If , , , then for any bounded sets and a.e. .
Theorem 3.1 Assume that conditions ()-() hold. Then there exists at least one mild solution for problem (1.1).
Proof Let us define an operator by
for all and show that the operator Q satisfies the hypothesis of Lemma 2.7. The proof consists of several steps.
-
(i)
Q is continuous. Let be a sequence in such that in . Then, in view of (), it follows that as . Now, for small and , we have
(3.3)
for . By assumption () together with (3.3)-(3.4), we obtain
Thus, is bounded and convex (W is defined by (3.1)).
For any , , we have
Similarly, for any and , we get
Using (3.5)-(3.6) and ()-(), we obtain
which implies that is a bounded operator.
-
(ii)
is equicontinuous, where W is defined by (3.1). For all and for each , we have by Lemma 2.4 that
(3.7)
Similarly, for all , with , , we get
Thus, from inequalities (3.7) and (3.8), we obtain
So, is equicontinuous.
Let . For any and , we know from Lemma 2.5 that there is a sequence such that
where we have used Lemma 2.3. Similarly, we have
Using the fact that there is a continuous function with satisfying the relation for any (), the above inequality takes the form
where , and . Again, by Lemma 2.5, for any , there is a sequence such that
Similarly, for , , we can obtain
Hence, by mathematical induction, for any positive integer n and , we obtain
By Lemma 2.2, we have
From Lemma 2.6, there exists a positive integer such that
Then
Thus, it follows by Lemma 2.7 that Q has at least one fixed point in , that is, the nonlocal integrodifferential equation (1.1) has at least one mild solution in . This completes the proof. □
Remark 3.2 In [38], the author discussed the nonlocal initial value problem by taking f to be compact in (1.1). From the above theorem, we notice that the key condition in [38] is no more required. So, Theorem 3.1 generalizes the related results in [38]. Furthermore, we extend the problem addressed in [23] to the impulse case with the nonlinearity of a more general form .
Theorem 3.3 If assumptions ()-() are satisfied, then there is at least one mild solution for (1.1) provided that
Proof We do not provide the proof of this theorem as it is similar to that of Theorem 3.1. □
For our final result, we introduce the following condition:
() Let be continuous and compact. Then there exists a positive constant such that for every .
Theorem 3.4 Suppose that conditions ()-() and ()-() hold. Then there exists at least one mild solution for (1.1) if there exists a constant r such that
Proof We omit the proof as it is similar to that of Theorem 3.1. This completes the proof. □
Example Consider a nonlocal problem of integrodifferential equations given by
with , . Let us take and define the operator A by with the domain = {: y, are absolutely continuous, , , }. The assumptions of Theorem 3.1 clearly hold for a large positive constant γ. Hence the conclusion of Theorem 3.1 applies to problem (3.9).
References
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, New York; 1983.
Dong Q, Li G: Existence of solutions for semilinear differential equations with nonlocal conditions in Banach spaces. Electron. J. Qual. Theory Differ. Equ. 2009., 2009: Article ID 47
Kato T: Quasilinear equations of evolution with applications to partial differential equations. Lect. Notes Math. 1975, 448: 25-70. 10.1007/BFb0067080
Kato T: Abstract evolution equation linear and quasilinear, revisited. Lect. Notes Math. 1993, 1540: 103-125. 10.1007/BFb0085477
Ntouyas SK, Tsamotas PC: Global existence for semilinear integrodifferential equations with delay and nonlocal conditions. Appl. Anal. 1997, 64: 99-105. 10.1080/00036819708840525
Anguraj A, Karthikeyan K: Existence of solutions for impulsive neutral functional differential equations with nonlocal conditions. Nonlinear Anal. 2009, 70: 2717-2721. 10.1016/j.na.2008.03.059
Guo DJ, Lakshmikantham V, Liu XZ: Nonlinear Integral Equations in Abstract Spaces. Kluwer Academic, Dordrecht; 1996.
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. World Scientific, Singapore; 1989.
Samoilenko AM, Perestyuk NA: Impulsive Differential Equations. World Scientific, Singapore; 1995.
Fan Z, Li G: Existence results for semilinear differential equations with nonlocal and impulsive conditions. J. Funct. Anal. 2010, 258: 1709-1727. 10.1016/j.jfa.2009.10.023
Liu JH: Nonlinear impulsive evolution equations. Dyn. Contin. Discrete Impuls. Syst. 1999, 6: 77-85.
Migorski S, Ochal A: Nonlinear impulsive evolution inclusions of second order. Dyn. Syst. Appl. 1997, 16: 679-687.
Byszewski L: Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal Cauchy problem. J. Math. Anal. Appl. 1991, 162: 494-505. 10.1016/0022-247X(91)90164-U
Byszewski L, Akca H: Existence of solutions of a semilinear functional differential evolution nonlocal problem. Nonlinear Anal. 1998, 34: 65-72. 10.1016/S0362-546X(97)00693-7
Aizicovici S, Mckibben M: Existence results for a class of abstract nonlocal Cauchy problems. Nonlinear Anal. 2000, 39: 649-668. 10.1016/S0362-546X(98)00227-2
Ji SC, Wen S: Nonlocal Cauchy problem for impulsive differential equations in Banach spaces. Int. J. Nonlinear Sci. 2010, 10(1):88-95.
Liang J, Liu JH, Xiao TJ: Nonlocal Cauchy problem governed by compact operator families. Nonlinear Anal. 2004, 57: 183-189. 10.1016/j.na.2004.02.007
Byszewski L, Lakshmikantham V: Theorems about the existence and uniqueness of solutions of nonlocal Cauchy problem in a Banach space. Appl. Anal. 1990, 40: 11-19.
Ntouyas S, Tsamotas P: Global existence for semilinear evolution equations with nonlocal conditions. J. Math. Anal. Appl. 1997, 210: 679-687. 10.1006/jmaa.1997.5425
Ntouyas SK, Tsamatos PC: Global existence for second order semilinear ordinary and delay integrodifferential equations with nonlocal conditions. Appl. Anal. 1997, 67(3-4):245-257. 10.1080/00036819708840609
Zhu T, Song C, Li G: Existence of mild solutions for abstract semilinear evolution equations in Banach spaces. Nonlinear Anal. 2012, 75: 177-181. 10.1016/j.na.2011.08.019
Agarwal RP, Ahmad B, Alsaedi A, Shahzad N: Existence and dimension of the set of mild solutions to semilinear fractional differential inclusions. Adv. Differ. Equ. 2012., 2012: Article ID 74
Lizama C, Pozo JC: Existence of mild solutions for a semilinear integrodifferential equation with nonlocal initial conditions. Abstr. Appl. Anal. 2012., 2012: Article ID 647103
Shaochun J, Gang L: A unified approach to nonlocal impulsive differential equations with the measure of noncompactness. Adv. Differ. Equ. 2012., 2012: Article ID 182
Xue X: Nonlocal nonlinear differential equations with a measure of noncompactness in Banach spaces. Nonlinear Anal. 2009, 70: 2593-2601. 10.1016/j.na.2008.03.046
Agarwal RP, Benchohra M, Seba D: On the application of measure of noncompactness to the existence of solutions for fractional differential equations. Results Math. 2009, 55: 221-230. 10.1007/s00025-009-0434-5
Dong Q, Li G: Existence of solutions for semilinear differential equations with nonlocal conditions in Banach spaces. Electron. J. Qual. Theory Differ. Equ. 2009., 2009: Article ID 47
Diagana T, Mophou GM, N’Guérékata GM: On the existence of mild solutions to some semilinear fractional integro-differential equations. Electron. J. Qual. Theory Differ. Equ. 2010., 2010: Article ID 58
Diagana T: Existence of pseudo-almost automorphic mild solutions to some nonautonomous partial evolution equations. Adv. Differ. Equ. 2011., 2011: Article ID 895079
Ji S, Li G: Existence results for impulsive differential inclusions with nonlocal conditions. Comput. Math. Appl. 2011, 62: 1908-1915. 10.1016/j.camwa.2011.06.034
Herzallah MAE, Baleanu D: Existence of a periodic mild solution for a nonlinear fractional differential equation. Comput. Math. Appl. 2012, 64(10):3059-3064. 10.1016/j.camwa.2011.12.060
Liang J, Liu JH, Xiao TJ: Nonlocal impulsive problems for nonlinear differential equations in Banach spaces. Math. Comput. Model. 2009, 49: 798-804. 10.1016/j.mcm.2008.05.046
Zhu L, Dong Q, Li G: Impulsive differential equations with nonlocal conditions in general Banach spaces. Adv. Differ. Equ. 2012., 2012: Article ID 10
Baleanu D, Mustafa OG, Agarwal RP: Asymptotically linear solutions for some linear fractional differential equations. Abstr. Appl. Anal. 2010., 2010: Article ID 865139
Baleanu D, Mustafa OG, Agarwal RP:Asymptotic integration of -order fractional differential equations. Comput. Math. Appl. 2011, 62: 1492-1500. 10.1016/j.camwa.2011.03.021
Debbouche A, Baleanu D, Agarwal RP: Nonlocal nonlinear integrodifferential equations of fractional orders. Bound. Value Probl. 2012., 2012: Article ID 78
Baleanu D, Diethelm DK, Scalas E, Trujillo JJ Series on Complexity, Nonlinearity and Chaos. In Fractional Calculus Models and Numerical Methods. World Scientific, Singapore; 2012.
Fan Z, Dong Q, Li G: Semilinear differential equations with nonlocal conditions in Banach spaces. Int. J. Nonlinear Sci. 2006, 2: 131-139.
Xue X: Semilinear nonlocal differential equations with measure of noncompactness in Banach spaces. J. Nanjing Univ. Math. Big. 2007, 24: 264-276.
Banas J, Goebel K Lecture Notes in Pure and Applied Mathematics 60. In Measure of Noncompactness in Banach Space. Marcel Dekker, New York; 1980.
Mönch H: Boundary value problems for nonlinear ordinary differential equations of second order in Banach spaces. Nonlinear Anal. 1980, 4: 985-999. 10.1016/0362-546X(80)90010-3
Bothe D: Multivalued perturbation of m -accretive differential inclusions. Isr. J. Math. 1998, 108: 109-138. 10.1007/BF02783044
Zhang X, Liu LS, Wu CX: Global solutions of nonlinear second order impulsive integrodifferential equations of mixed type in Banach spaces. Nonlinear Anal. 2007, 67: 2335-2349. 10.1016/j.na.2006.08.033
Lou B: Fixed points for operators in a space of continuous functions and applications. Proc. Am. Math. Soc. 1999, 127: 2259-2264. 10.1090/S0002-9939-99-05211-9
Liu LS, Guo F, Wu CX, Wu YH: Existence theorems of global solutions for nonlinear Volterra type integral equations in Banach spaces. J. Math. Anal. Appl. 2005, 309: 638-649. 10.1016/j.jmaa.2004.10.069
Acknowledgements
The authors thank the reviewers for their useful comments that led to the improvement of the original manuscript. The research of B. Ahmad was partially supported by Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
Each of the authors, BA, KM and KK, contributed to each part of this study equally and read and approved the final version of the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahmad, B., Malar, K. & Karthikeyan, K. A study of nonlocal problems of impulsive integrodifferential equations with measure of noncompactness. Adv Differ Equ 2013, 205 (2013). https://doi.org/10.1186/1687-1847-2013-205
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-205