A semigroup-like Property for Discrete Mittag-Leffler Functions

Abstract

Discrete Mittag-Leffler function $E_{\bar{\alpha }}\left(\lambda ,z\right)$ of order 0 < α ≤ 1, $E_{\bar{1}}\left(\lambda ,z\right)={\left(1-\lambda \right)}^{-z}$, λ ≠ 1, satisfies the nabla Caputo fractional linear difference equation

$$C^{}{\nabla }_0^{\alpha }x\left(t\right)=\lambda x\left(t\right),x\left(0\right)=1,t\in {\mathbb{N}}_1=\left\{1,2,3,\dots \right\}.$$

Computations can show that the semigroup identity

$$E_{\bar{\alpha }}\left(\lambda ,z_1\right)E_{\bar{\alpha }}\left(\lambda ,z_2\right)=E_{\bar{\alpha }}\left(\lambda ,z_1+z_2\right)$$

does not hold unless λ = 0 or α = 1. In this article we develop a semigroup property for the discrete Mittag-Leffler function $E_{\bar{\alpha }}\left(\lambda ,z\right)$ in the case α ↑ 1 is just the above identity. The obtained semigroup identity will be useful to develop an operator theory for the discrete fractional Cauchy problem with order α ∈ (0, 1).

1 Introduction and Preliminaries

The fractional calculus started to be investigated deeply in both theorical and applied view points. One of the main reasons of the fast development of this type of calculus is that it incorporates, as a particular case, the classical calculus. Starting from this interesting point it is natural to ask if there is an extension of the fractional calculus and even more precisely if this generalization could find us new dimensions of some problems within the complex systems which up to now were not solved properly as in Biology, nanotechnology and medicine [1–6]. Mittag-Leffler functions play a very important role in the theory of fractional differential equations [1–4].

Recently there is a huge effort on the line of discretizing the fractional calculus operators and its applications in the control theory and the corresponding variational principles [9–17]. In our opinion the discrete fractional operators can play a crucial role both from the theoretical and applied point of view. However the combinations of the techniques from both fields are not always straithforward namely because the fractional operators are non-local. However, we expect that this new unification will provide new tools in understanding the hyper-complex dynamical systems.

In this article, the main aim is to establish a semi-group property for discrete Mittag-Leffler functions.

This article is organized as follows: The rest of this section contains definitions and preliminary concepts regarding the rising factorial function, the discrete Mittaf-Leffler functions, Caputo fractional difference and the discrete convolution. In Section 2, we find the nabla discrete transforms of certain discrete Mittag-Leffler functions by making use of the discrete convolution theorem, which will be helpful to proceed in obtaining our main results. Finally, Section 3 deals with a semigroup property for discrete Mittag-Leffler functions and some examples are given to illustrate our results.

For the sake of the nabla fractional calculus we have the following definition

Definition 1. (i) For a natural number m, the m rising (ascending) factorial of t is defined by

$$t^{\bar{m}}=\prod _{k=0}^{m-1}\left(t+k\right),t^{\bar{0}}=1.$$

(1)

(ii) For any real number the α rising function is defined by

$$t^{\bar{\alpha }}=\frac{\mathrm{\Gamma }\left(t+\alpha \right)}{\mathrm{\Gamma }\left(t\right)},t\in ℝ\backslash \left\{\dots ,-2,-1,0\right\},0^{\bar{\alpha }}=0$$

(2)

Regarding the rising factorial function we observe the following:

(i)

$$\nabla \left(t^{\bar{\alpha }}\right)=\alpha t^{\overline{\alpha -1}}$$

(3)

(ii)

$${\nabla }_t{\left(s-t\right)}^{\bar{\alpha }}=\alpha {\left(s-\rho \left(t\right)\right)}^{\overline{\alpha -1}},$$

(4)

where ρ(t) = t - 1.

Definition 2. The nabla discrete Laplace transform for a function f defined on ${\mathbb{N}}_0$ is defined by

$$\mathcal{N}f\left(z\right)=\sum _{t=1}^{\infty }{\left(1-z\right)}^{t-1}f\left(t\right)$$

(5)

If f(t, s) is a function of two variables, we state explicitly to specify to which parameter we apply the transform.

Lemma 1. [11] For any $\alpha \in ℝ\backslash \left\{\dots ,-2,-1,0\right\}$,

• (i)$\mathcal{N}\left(t^{\overline{\alpha -1}}\right)\left(z\right)=\frac{\mathrm{\Gamma }\left(\alpha \right)}{s^{\alpha }}$, |1 - z| < 1,

• (ii)$\mathcal{N}\left(t^{\overline{\alpha -1}}{b}^{-t}\right)\left(z\right)=\frac{b^{\alpha -1}\mathrm{\Gamma }\left(\alpha \right)}{{\left(s+b-1\right)}^{\alpha }}$, |1 - z| < b.

Definition 3. (Nabla Discrete Mittag-Leffler) For $\lambda \in ℝ$ and α, β, $z\in ℂ$ with Re(α) > 0, the nabla discrete Mittag-Leffler functions are defined by

$$E_{\overline{\alpha ,\beta }}\left(\lambda ,z\right)=\sum _{k=0}^{\infty }{\lambda }^k\frac{z^{\overline{k\alpha +\beta -1}}}{\mathrm{\Gamma }\left(\alpha k+\beta \right)}.$$

(6)

For β = 1, it is written that

$$E_{\bar{\alpha }}\left(\lambda ,z\right)\triangleq E_{\overline{\alpha ,1}}\left(\lambda ,z\right)=\sum _{k=0}^{\infty }{\lambda }^k\frac{z^{\overline{k\alpha }}}{\mathrm{\Gamma }\left(\alpha k+1\right)}.$$

(7)

Definition 4. For 0 < α ≤ 1 the α-order Caputo fractional derivative of a function f, which is defined on ${\mathbb{N}}_0$, is defined by

$$\begin{array}{ll}\hfill C^{}{\nabla }_0^{\alpha }f\left(t\right)& ={\nabla }_0^{-\left(1-\alpha \right)}\nabla f\left(t\right)\\ =\frac{1}{\mathrm{\Gamma }\left(1-\alpha \right)}\sum _{s=1}^t{\left(t-\rho \left(s\right)\right)}^{\overline{-\alpha }}\nabla f\left(s\right),\end{array}$$

where ρ(s) = s - 1 and ${\nabla }_0^{-\alpha }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\sum }_{s=1}^t{\left(t-\rho \left(s\right)\right)}^{\overline{\alpha -1}}f\left(s\right)$ is the nabla left fractional sum of order α.

Note that if f is defined on ${\mathbb{N}}_0$, then $C^{}{\nabla }_0^{\alpha }f\left(t\right)$ is defined on ${\mathbb{N}}_1=\left\{1,2,3,\dots \right\}$.

Example 1. Let 0 < α ≤ 1, $a\in ℝ$ and consider the nabla left Caputo nonhomogeneous fractional difference equation

$$C^{}{\nabla }_0^{\alpha }y\left(t\right)=\lambda y\left(t\right)+f\left(t\right),y\left(0\right)=a_0,t\in {\mathbb{N}}_0.$$

(8)

The solution of (8) has the form

$$y\left(t\right)=a_0{E}_{\bar{\alpha }}\left(\lambda ,t\right)+\sum _{s=1}^t{E}_{\overline{\alpha ,\alpha }}\left(\lambda ,t-\rho \left(s\right)\right)f\left(s\right).$$

(9)

Remark 1. If we solve the nabla discrete fractional system (8) with α = 1 and a₀ = 1 we obtain the following solution

$$y\left(t\right)=\sum _{k=0}^{\infty }{\lambda }^k\frac{t^{\bar{k}}}{k!}+\sum _{s=1}^t\sum _{k=0}^{\infty }{\lambda }^k\frac{{\left(t-\rho \left(s\right)\right)}^{\bar{k}}}{k!}f\left(s\right).$$

The first part of the solution is the nabla discrete exponential function ${\stackrel{⌢}{e}}_{\lambda }\left(t,0\right)={\left(1-\lambda \right)}^{-t}$. For the sake of more comparisons see reference ([18], p. 118).

Definition 5. Let $s\in ℝ$, 0 < α < 1 and $f:{\mathbb{N}}_0\to ℝ$ be a function. The nabla discrete convolution of $g_s^{\alpha }\left(t\right)={\left(t+s\right)}^{\bar{\alpha }}$ with f is defined by

$$\left(g_s^{\alpha }*f\right)\left(t\right)=\sum _{\tau =1}^t{\left(t+s-\rho \left(\tau \right)\right)}^{\bar{\alpha }}f\left(\tau \right).$$

(10)

2 Discrete Laplace of Mittag-Leffler Type and Convolution Type Functions

Proposition 1. For any $\alpha \in ℝ\backslash \left\{\dots ,-2,-1,0\right\}$, $s\in ℝ$ and f defined on ${\mathbb{N}}_0$ we have

$$\left(\mathcal{N}\left(g_s^{\alpha }*f\right)\right)\left(z\right)=\left(\mathcal{N}{g}_s^{\alpha }\right)\left(z\right)\left(\mathcal{N}f\right)\left(z\right).$$

(11)

Proof.

$$\begin{array}{ll}\hfill \left(\mathcal{N}\left(g_s^{\alpha }*f\right)\right)\left(z\right)& =\sum _{t=1}^{\infty }{\left(1-z\right)}^{t-1}\sum _{\tau =1}^t{\left(t+s-\rho \left(\tau \right)\right)}^{\bar{\alpha }}f\left(\tau \right)\\ =\sum _{\tau =1}^{\infty }\sum _{t=\tau }^{\infty }{\left(1-z\right)}^{t-1}{\left(t+s-\rho \left(\tau \right)\right)}^{\bar{\alpha }}f\left(\tau \right)\\ =\sum _{\tau =1}^{\infty }\sum _{r=s+1}^{\infty }{\left(1-z\right)}^{r+\tau -s-2}{r}^{\bar{\alpha }}f\left(\tau \right)\\ =\sum _{\tau =1}^{\infty }{\left(1-z\right)}^{\tau -1}f\left(\tau \right)\sum _{r=s+1}^{\infty }{\left(1-z\right)}^{r-1-s}{r}^{\bar{\alpha }}\\ =\left(\mathcal{N}{g}_s^{\alpha }\right)\left(z\right)\left(\mathcal{N}f\right)\left(z\right).\end{array}$$

(12)

   □

Lemma 2. Let f be defined on ${\mathbb{N}}_0$. Then

$$(\mathcal{N}\nabla \left(f\left(t\right)\right)\left(z\right)=z\left(\mathcal{N}f\right)\left(z\right)-f\left(0\right).$$

(13)

Proof.

$$\begin{array}{ll}\hfill (\mathcal{N}\nabla \left(f\left(t\right)\right)\left(z\right)& =\sum _{t=1}^{\infty }{\left(1-z\right)}^{t-1}f\left(t\right)-\sum _{t=1}^{\infty }{\left(1-z\right)}^{t-1}f\left(t-1\right)\\ =\sum _{t=1}^{\infty }{\left(1-z\right)}^{t-1}f\left(t\right)-\sum _{t=0}^{\infty }{\left(1-z\right)}^{t}f\left(t\right)\\ =\left(\mathcal{N}f\right)\left(z\right)-f\left(0\right)-\left(1-z\right)\sum _{t=1}^{\infty }{\left(1-z\right)}^{t-1}f\left(t\right)\\ =\left(\mathcal{N}f\right)\left(z\right)-f\left(0\right)-\left(1-z\right)\left(\mathcal{N}f\right)\left(z\right)\\ =z\left(\mathcal{N}f\right)\left(z\right)-f\left(0\right).\end{array}$$

(14)

   □

Lemma 3. Let f be defined on ${\mathbb{N}}_0$ and 0 < α ≤ 1. Then

$$\left({\mathcal{N}}^C{\nabla }_0^{\alpha }f\right)\left(z\right)=z^{\alpha }\left(\mathcal{N}f\right)\left(z\right)-z^{\alpha -1}f\left(0\right).$$

(15)

Proof. By the help of Lemma 1, Proposition 1 and Lemma 2 we have

$$\begin{array}{ll}\hfill \left({\mathcal{N}}^C{\nabla }_0^{\alpha }f\right)\left(z\right)& =\left(\mathcal{N}\frac{1}{\mathrm{\Gamma }\left(1-\alpha \right)}{g}_0^{-\alpha }*\nabla f\right)\left(z\right)\\ =z^{\alpha -1}\left(\mathcal{N}\nabla f\right)\left(z\right)\\ =z^{\alpha -1}\left[z\left(\mathcal{N}f\right)\left(z\right)-f\left(0\right)\right]\\ =z^{\alpha }\left(\mathcal{N}f\right)\left(z\right)-z^{\alpha -1}f\left(0\right).\end{array}$$

(16)

   □

Lemma 4. Let 0 < α ≤ 1 and f be defined on ${\mathbb{N}}_0$. Then,

(i) $\left(\mathcal{N}{E}_{\bar{\alpha }}\left(\lambda ,t\right)\right)\left(z\right)=\frac{z^{\alpha -1}}{z^{\alpha }-\lambda }$.

(ii) $\left(\mathcal{N}{E}_{\overline{\alpha ,\alpha }}\left(\lambda ,t\right)\right)\left(z\right)=\frac{{\lambda }^2}{z^{\alpha }-\lambda }$

Proof. (i) From Example 1 we know that

$$C^{}{\nabla }_0^{\alpha }{E}_{\bar{\alpha }}\left(\lambda ,t\right)=\lambda E_{\bar{\alpha }}\left(\lambda ,t\right).$$

Apply the nabla discrete Laplace transform to both sides, then Lemma 3 yields that

$$z^{\alpha }\left(\mathcal{N}{E}_{\bar{\alpha }}\left(\lambda ,t\right)\right)\left(z\right)-z^{\alpha -1}=\lambda \left(\mathcal{N}{E}_{\bar{\alpha }}\left(\lambda ,t\right)\right)\left(z\right).$$

Hence, it follows.

• (ii) First it is easy to see that $\nabla E_{\bar{\alpha }}\left(\lambda ,t\right)=-{\lambda }^{-1}{E}_{\overline{\alpha ,\alpha }}\left(\lambda ,t\right)$. If we apply 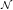and make use of (i) and Lemma 2, then we have that

  $$\begin{array}{ll}\hfill \mathcal{N}{E}_{\overline{\alpha ,\alpha }}(\lambda ,t))\left(z\right)& =\lambda \left[z\left(\mathcal{N}{E}_{\bar{\alpha }}\left(\lambda ,t\right)\right)\left(z\right)-E_{\bar{\alpha }}\left(\lambda ,0\right)\right]\\ =\lambda \left[\frac{z^{\alpha }}{z^{\alpha }-\lambda }-1\right]\\ =\frac{{\lambda }^2}{z^{\alpha }-\lambda }.\end{array}$$

   □

3 A discrete Mittag-Leffler Semigroup Property

By direct calculations it can be showed that the following semigroup property for discrete Mittag-Leffler functions

$$E_{\bar{\alpha }}\left(\lambda ,z_1\right)E_{\bar{\alpha }}\left(\lambda ,z_2\right)=E_{\bar{\alpha }}\left(\lambda ,z_1+z_2\right)$$

does not hold unless λ = 0 or α = 1. For more consistency, we next show how certain discrete Mittag-Leffler functions do not satisfy the above mentioned semigroup property.

Example 2. For 0 < α ≤ 1 and λ ≠ 1 we have

$$E_{\bar{\alpha }}\left(\lambda ,1\right)=\sum _{k=0}^{\infty }\frac{{\lambda }^k{1}^{\overline{\alpha k}}}{\mathrm{\Gamma }\left(\alpha k+1\right)}=\sum _{k=0}^{\infty }{\lambda }^k=\frac{1}{1-\lambda }$$

and

$$E_{\bar{\alpha }}\left(\lambda ,2\right)=\sum _{k=0}^{\infty }{\lambda }^k\left(\alpha k+1\right)=\frac{1+\lambda \left(\alpha -1\right)}{{\left(1-\lambda \right)}^2}.$$

Then, clearly

$$E_{\bar{\alpha }}\left(\lambda ,1\right)E_{\bar{\alpha }}\left(\lambda ,1\right)\ne E_{\bar{\alpha }}\left(\lambda ,1+1\right)$$

Theorem 1. For every real λ and 0 < α < 1 the following holds

$$\begin{array}{c}\alpha \sum _{\tau =1}^s\sum _{r=1}^t{\left(t+s-\rho \left(\tau \right)-\rho \left(r\right)\right)}^{\overline{-\alpha -1}}{E}_{\bar{\alpha }}\left(\lambda ,\tau \right)E_{\bar{\alpha }}\left(\lambda ,r\right)=\\ \sum _{\tau =1}^{t+s}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}{E}_{\bar{\alpha }}\left(\lambda ,\tau \right)-\sum _{\tau =1}^{s+1}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}{E}_{\bar{\alpha }}\left(\lambda ,\tau \right)-\sum _{\tau =1}^t{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}{E}_{\bar{\alpha }}\left(\lambda ,\tau \right),\end{array}$$

(17)

for all t, $s\in {\mathbb{N}}_1$.

Proof. For the sake of simplicity we set $f\left(t\right)=E_{\bar{\alpha }}\left(\lambda ,t\right)$. By Definition 4 we have that for all t, $s\in {\mathbb{N}}_1$,

$$\begin{array}{ll}\hfill t_C^{}{\nabla }_0^{\alpha }f\left(t+s\right)& =\frac{1}{\mathrm{\Gamma }\left(\alpha -1\right)}\sum _{\tau =1}^t{\left(t-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}{\nabla }_{\tau }f\left(\tau +s\right)\\ =\frac{1}{\mathrm{\Gamma }\left(\alpha -1\right)}\sum _{\tau =s+1}^{t+s}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{\alpha -1}}{\nabla }_{\tau }f\left(\tau \right)\\ =r_C^{}{\nabla }_0^{\alpha }f\left(r\right){|}_{r=t+s}-\frac{1}{\mathrm{\Gamma }\left(\alpha -1\right)}\sum _{\tau =1}^s{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}{\nabla }_{\tau }f\left(\tau \right)\\ =\lambda f\left(t+s\right)-\frac{1}{\mathrm{\Gamma }\left(\alpha -1\right)}\sum _{\tau =1}^s{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}{\nabla }_{\tau }f\left(\tau \right).\end{array}$$

(18)

In the last equality the fact that $E_{\bar{\alpha }}\left(\lambda ,t\right)$ solves Eq.(8) is used. Applying the nabla discrete transform 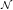with respect to t to both sides of (18), we get by Lemma 3 that

$$z^{\alpha }\left(\mathcal{N}{f}_s\right)\left(z\right)-z^{\alpha -1}f\left(s\right)=\lambda \left(\mathcal{N}{f}_s\right)\left(z\right)-\frac{1}{\mathrm{\Gamma }\left(-\alpha \right)}\sum _{\tau =1}^s\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}\right)\left(z\right){\nabla }_{\tau }f\left(\tau \right),$$

(19)

where $\left(\mathcal{N}{f}_s\right)\left(z\right)$ and $\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}\right)\left(z\right)$ are the nabla discrete transforms of f(t + s) and ${\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}$ with respect to t, respectively. By applying the nabla summation by parts and making use of (4) we have that

$$\begin{array}{c}\sum _{\tau =1}^s\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}\right)\left(z\right){\nabla }_{\tau }f\left(\tau \right)=\\ f\left(\tau \right)\left(\mathcal{N}{\left(t+s-\tau \right)}^{\overline{-\alpha }}\right)\left(z\right){|}_{\tau =0}^s-\alpha \sum _{\tau =1}^s\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha -1}}\right)\left(z\right).\end{array}$$

(20)

By Lemma 1 (i), we arrive at

$$\begin{array}{ll}\hfill \sum _{\tau =1}^s\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}\right)\left(z\right){\nabla }_{\tau }f\left(\tau \right)& =\frac{f\left(s\right)\mathrm{\Gamma }\left(1-\alpha \right)}{z^{1-\alpha }}-\left(\mathcal{N}{\left(t+s\right)}^{\overline{-\alpha }}\right)\left(z\right)\\ -\alpha \sum _{\tau =1}^s\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha -1}}\right)\left(z\right),\end{array}$$

(21)

which combining with the equality (19) leads to that

$$\begin{array}{c}\mathrm{\Gamma }\left(1-\alpha \right)z^{\alpha -1}\left(\mathcal{N}{f}_s\right)\left(z\right)=\\ \frac{z^{\alpha -1}}{z^{\alpha }-\lambda }\left(\mathcal{N}{\left(t+s\right)}^{\overline{-\alpha }}\right)\left(z\right)-\alpha \sum _{\tau =1}^s\left(\mathcal{N}{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha -1}}\right)\left(z\right)\frac{z^{\alpha -1}}{z^{\alpha }-\lambda }f\left(\tau \right).\end{array}$$

(22)

Then applying the inverse nabla discrete Laplace transform to both sides of (22), we get that

$$\begin{array}{c}\sum _{\tau =1}^t{\left(t-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}f\left(\tau +s\right)=\\ \sum _{\tau =1}^t{\left(t+s-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}f\left(\tau \right)+\alpha \sum _{\tau =1}^s\sum _{r=1}^{t}f\left(r\right){\left(t+s-\rho \left(\tau \right)-\rho \left(r\right)\right)}^{\overline{-\alpha -1}}f\left(\tau \right).\end{array}$$

(23)

Arranging the limit of the sum in the left hand sum of (23) and making use of Proposition 1 it follows that

$$\begin{array}{c}\sum _{\tau =s+1}^{s+t}{\left(t-\rho \left(\tau \right)\right)}^{\overline{-\alpha }}f\left(\tau \right)=\\ \sum _{\tau =1}^t{(t+s-\rho (\tau \left)\right)}^{\overline{-\alpha }}f\left(\tau \right)+\alpha \sum _{\tau =1}^s\sum _{r=1}^{t}f\left(r\right){\left(t+s-\rho \left(\tau \right)-\rho \left(r\right)\right)}^{\overline{-\alpha -1}}f\left(\tau \right).\end{array}$$

(24)

Splitting the sum in the left hand side of (24) yields directly equality (17).

   □

Remark 2. We note that for α = 1, the summations in (17) are divergent. However, it can be shown that the semigroup property for$E_{\bar{1}}\left(\lambda ,t\right)={ê}_{\lambda }\left(t,0\right)={\left(1-\lambda \right)}^{-t}$ is just the limit case state of equality (17) as α↑ 1. Indeed, if we multiply both sides of (17) with (1 - α) and use summation by parts, then, letting α ↑ 1 we get that the limit state of the left is $E_{\bar{1}}\left(\lambda ,t\right)E_{\bar{1}}\left(\lambda ,s\right)$ and of the right is $E_{\bar{1}}\left(\lambda ,t+s\right)$.