- Research
- Open access
- Published:
Existence and stability of almost periodic solutions for impulsive differential equations
Advances in Difference Equations volume 2012, Article number: 34 (2012)
Abstract
In this article, by using Schauder's fixed point theorem, we study the existence of almost periodic solutions for abstract impulsive differential equations. In addition, sufficient conditions for their asymptotic stability are obtained by means of generalized Gronwall-Bellman inequality.
1 Introduction
When a dynamical system processes aftereffect and state changing by jumps, this system is called an impulsive differential system. Because of the needs of modern technology, such as simulation in physics, biology, populations dynamics, control theory, industrial robotics, etc., the study of impulsive differential equations attracts more and more researchers' interest, see [1–8]. There are many articles [9–16] about existence of solutions, periodic solutions and stability for impulsive differential equations. But, only a few articles [17, 18] have studied the existence of almost periodic solutions to abstract impulsive differential equations in Banach space.
By means of fractional powers of operators and Contraction mapping principle, Stamov and Alzabut in [17] studied the existence and uniqueness of exponentially stable almost periodic solutions for the abstract impulsive differential equation as follows:
where G k (⋅) are continuous impulsive operators.
In [18], by using Contraction mapping principle, Henriquez et al. studied the existence of almost periodic solutions to the following impulsive differential equation:
To the best of authors' knowledge, most of the previous research on existence of almost periodic solutions for impulsive differential equations was based on Contraction mapping principle. Lipschitz condition is necessary. Motivated by the studies in [8, 12, 13, 19–21], in this article we use Schauder's fixed point theorem and generalized Gronwall-Bellman inequality to investigate the existence and asymptotic stability of almost periodic solutions to the following impulsive differential equation:
where A(t) : X → X are closed linear operators on a Banach space (X, || ⋅ ||), f, I i , and t i satisfy suitable conditions that will be established later and the symbol Δξ (t) represents the jump of the function ξ at t, which is defined by Δξ (t) = ξ (t+) − ξ(t−).
2 Preliminaries
In this section, we give some notations, definitions, and preliminary facts about impulsive differential equations. Throughout this article, we denote by (X, || ⋅ ||) a Banach space and by R the set of real numbers. The symbol L(X) stands for the Banach space formed by all bounded linear operators form X into X endowed with the uniform operator topology. For a linear operator A, ρ(A) is its resolvent set and for λ ∈ ρ(A), R(λ,A) = (λI − A)−1 denotes its resolvent operator. Let  be the set consisting of all real sequences {t
i
}i∈Zsuch that α = inf i∈Z(ti+ 1- t
i
)> 0 and limi→−∞t
i
= −∞, limi→−∞t
i
= ∞.
be the set consisting of all real sequences {t
i
}i∈Zsuch that α = inf i∈Z(ti+ 1- t
i
)> 0 and limi→−∞t
i
= −∞, limi→−∞t
i
= ∞.
For , let PC(R, X) be the space formed by all piecewise continuous functions ϕ : R → X such that ϕ(⋅) is continuous at t for any t ∉ {t i }i∈Zand for all i ∈ Z; let PC(R × X, X) be the space formed by all piecewise continuous functions ϕ : R × X → X such that for any x∈ X, ϕ(⋅, x) is continuous at t for any t ∉ {t i }i∈Zand for all i ∈ Z and for any t ∈ R, ϕ(t, ⋅) is continuous at x ∈ X.
For a function f ∈ PC (R, X) (respectively PC(R × X, X)) and τ ∈ R, the translation of f by τ is the function R τ f(t) = f(t + τ) (respectively, R τ f(t, x) = f(t + τ, x)).
A number τ ∈ R is called an ε-translation number of the function f ∈ PC(R, X) (PC( R × X, X )) if
for all t ∈ R which satisfies |t - t i | > ε. Denote by the set of all ε-translation numbers of f.
Definition 2.1 (D1) A function ϕ ∈ PC(R, X)(PC(R × X, X)) is said to be piecewise almost periodic if the following conditions are fulfilled:
-
(1)
, j ∈ Z, are equipotentially almost periodic.
-
(2)
For any ε > 0 (every compact subset K of X), there exists a positive number δ = δ (ε)(δ = δ(ε, K)) such that if the points t′ and t″ belong to a same continuity and |t′ - t″| < δ, then ||ϕ (t′) - ϕ(t″)|| < ε (||ϕ(t′, x) - ϕ(t″, x)|| < ε, for any x ∈ K).
-
(3)
For every ε > 0 (every compact subset K of X), is a relatively dense set in R.
We denote by AP T (R, X)(AP T (R × X, X)) the space of all piecewise almost periodic functions. Obviously, the space AP T (R, X)(AP T (R × X, X)) endowed with the norm of the uniform convergence || ⋅ || is a Banach space.
(D2) A set B ⊆ AP T (R, X) is called a uniformly piecewise almost periodic family if it is uniformly bounded and if given ε > 0, then is relatively dense in R.
Obviously, if f ∈ AP T (R × X, X) and for each compact set K ⊆ X, f(t, x) : R × X → X is uniformly continuous in x ∈ K uniformly in t ∈ R, then {f(⋅, x) : x ∈ K} is a uniformly piecewise almost periodic family
Lemma 2.2[18] Let ϕ ∈ AP T (R, X), then the range of ϕ, R(ϕ), is a relatively compact subset of X.
Lemma 2.3 If a set B ⊆ AP T (R, X) is relatively compact, then ∪f∈BR ( f ) is a relatively compact set in X.
Proof Since B is a relatively compact set, for any ε > 0, there exists a finite number of functions f1, f2, ..., f N ∈ B such that for any f ∈ B, there exists a number i ∈ {1, 2, ..., N}, then
By Lemma 2.2, R(f1), R(f2), ..., R(f N ) are relatively compact sets in X, so is ∪1≤ i≤ NR ( f i ), that is, ∪1≤ i≤ NR ( f i ) can be embedded in a finite number of balls of radius . Let us denote by x1, x2, ..., x n the centers of the balls of radius which cover the set ∪1≤ i≤ NR (f i ). For any t ∈ R, f ∈ B, let x i be the center of the ball of radius which contains f i (t), we have
This show that Uf∈BR(f) is covered for any ε > 0 by a finite number of balls of radius ε. This proof is complete.
For the operators {A(t) : t ∈ R}, we make the following assumption (H) :
(H1) {A(t) : t ∈ R} are linear operators on a Banach space X and there are constants K ≥ 0, r ∈ R and such that
for λ ∈ ρ(A(t)) ∩ ∑(ϕ, r) and t ∈ R, where ∑(ϕ, r) = {r} ∪ {λ : | arg(λ - r)| ≤ ϕ}.
(H2) There are constants L ≥ 0 and µ, ν ∈ (0, 1] with µ + ν > 1 such that
for A r (t) = A(t) -r, t, s ∈ R and | arg λ| < ϕ.
(H3) R (λ, A(⋅)) ∈ AP (L(X)).
(H4) The evolution family {T(t, s) : t, s ∈ R, t ≥ s} generated by {A(t) : t ∈ R} is exponentially stable, i.e., there exists numbers M > 0, w > 0, such that ||T(t, s)|| ≤ Me-w(t - s), t ≥ s, t, s ∈ R.
(H5) For fixed t, s ∈ R, t ≥ s, the operator T(t, s) : X → X is compact, that is, T(t, s) is continuous and maps a bounded set into a relatively compact set.
(H6) For each x ∈ X, T(t+h, t)x → x as h → 0+ uniformly for t ∈ R, i.e., {T(t, s) : t ≥ s} is uniformly continuous.
Operators {A(t) : t ∈ R} fulfilling (H1) and (H2) are called sectorial, see [22–25].
Lemma 2.4[25] Assume that the conditions (H1)-(H4) hold. Then for each ε > 0 and δ > 0, there is a relatively dense set Ωε,δsuch that
This property can be abbreviated by writing T ∈ AP(L(X)).
Lemma 2.5[18] Assume that f ∈ AP T (R, X), T ∈ AP(L(X)), the sequence {x i : i ∈ Z} is almost periodic, and , j ∈ Z, are equipotentially almost periodic. Then for each ε > 0 there exist relatively dense sets of R and of Z satisfying:
-
(i)
||f(t + τ) - f(t)|| < ε for all t ∈ R, |t - t i | > ε, and i ∈ Z.
-
(ii)
for all t, s ∈ R, |t - s| > 0, |t - t i | > ε, |s - t i | > ε, and i ∈ Z; w > 0 is the same as in (H4).
-
(iii)
||x i + q- x i || < ε for all and i ∈ Z.
-
(iv)
for all and i ∈ Z.
Definition 2.6 A bounded function u(t) : R → X is called a mild solution of (1.3) if for any t ∈ R, σ < t i < t < ti+ 1,
Under the assumption (H), ||T(t, σ)|| ≤ Me-w(t - σ)for all t > σ. Let σ → - ∞, then ||T(t, σ) || → 0 and so, the above formula can be replaced by
In fact, for t > σ,
so that,
The following lemma is a criterion of relative compactness for subsets in AP T (R, X), its proof is similar to the case in AP(R, X) (e.g., see [26]).
Lemma 2.7 Let . Then 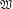 is relatively compact in AP
T
(R, X) if and only if the following properties hold true:
is relatively compact in AP
T
(R, X) if and only if the following properties hold true:
-
(i)
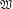 is equicontinuous, which means that for any ε > 0, there exists δ(ε) > 0 such that for any one has || f (t) - f(s) || < ε if |t - s| < δ(ε) and t and s in a same continuity.
is equicontinuous, which means that for any ε > 0, there exists δ(ε) > 0 such that for any one has || f (t) - f(s) || < ε if |t - s| < δ(ε) and t and s in a same continuity. -
(ii)
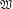 is equi-almost-periodic, which means that for each ε > 0 there exists l(ε) > 0 such that any interval (a, a + l) ⊂ R contains a number τ that is an ε- almost period for all .
is equi-almost-periodic, which means that for each ε > 0 there exists l(ε) > 0 such that any interval (a, a + l) ⊂ R contains a number τ that is an ε- almost period for all . -
(iii)
For fixed t ∈ R, the set is relatively compact in the space X.
Definition 2.8[27] The solution x(t, σ, ϕ) of (1.3) is said to be stable, if for any σ ∈ R, ε > 0, there is a number δ = δ(σ, ε) > 0, such that for any other solution y(t, σ, ψ) of (1.3) satisfying ||φ - ψ|| < δ then ||x(t, σ, φ)-y(t, σ, ψ)|| < ε.
x(t, σ, φ) is said to be asymptotically stable if it is stable and if there is a constant b > 0 such that ||φ - ψ|| < b, then limt → ∞||x(t, σ, φ) - y(t, σ, ψ)|| = 0.
Lemma 2.9 ([1], generalized Gronwall-Bellman inequality) Let a nonnegative function u(t) ∈ PC(R, X) satisfy for t ≥ t0 the inequality
where C ≥ 0, β i ≥ 0, v(τ) > 0, and are discontinuity points of first type of the function u(t). Then the following estimate holds for the function u(t),
3 Main results
In order to get the almost periodic solutions of (1.3), in addition to the previous assumptions, we require the following additional assumptions:
(A1) ∀L > 0, C L = supt∈R, ||x|| ≤ L|| f(t, x)|| < ∞, C = supi∈Z|| I i || < ∞. Moreover, there exists a number L0 > 0, such that and .
(A2) For each compact set K ⊆ X, f(t, x) ∈ AP T (R × X, X) is uniformly continuous in x ∈ K uniformly in t ∈ R; I i (x) is almost periodic in i ∈ Z uniformly in x ∈ K and is a uniformly continuous function defined on the set K ⊆ X for all i ∈ Z.
(A3) Let {x n } ⊆ AP T (R, X) be uniformly bounded in R and uniformly convergent in each compact set of R, then {f(⋅, x n (⋅))} is relatively compact in PC(R, X).
(A4) There exists a compact set K0 ⊆ X, for any r > 0,
such that R(x) ⊆ K0 for all x ∈ B r , where the choice of is similar to that of Lemma 2.5.
Theorem 3.1 Suppose the conditions (H), (A1)-(A4) hold, then (1.3) has a mild piecewise almost periodic solution.
Proof Define the operator Γ on AP T (R, X) by
Now we use Schauder's fixed point theorem to prove that Γ has a fixed point in AP T (R, X).
For any n ∈ N, let
and
By (A4), for any . Note that , so {u(t): u ∈ B, t ∈ R} ⊆ K0. By (A2), {f(⋅, x) : x ∈ K0} and {I i (x) : x ∈ K0} are uniformly piecewise almost periodic families. Then by Lemma 2.5, there exists a relatively dense set of R. As the proof of [[28], Theorem 2.6] for the case of AP(R, X), one shows that for each n ∈ N, the set is relatively compact and so is B. Obviously, B is a nonempty closed convex set. For any u ∈ B,
In order to estimate the second term on the right-hand side of the above formula, we assume t j ≤ t < tj+ 1, j ∈ Z, so
and,
Thus
By (A2), for any n ∈ N, there exists a number , if ||x - y|| ≤ δ then and for all i ∈ Z.
For any (∀n ∈ N) and ,
So, for ,
Similarly, for q ∈ Z with , we have
Then,
By Lemmas 2.4, 2.5, Equations (3.1) and (3.2), we have
and
Therefore, for any n ∈ N, there exists a relatively dense set of R, for ,
That is, . Since n is arbitrary, , that is ΓB ⊆ B.
We will show Γ is compact. To this end, first we show Γ is continuous. In fact, By (A2), for the above , δ > 0 for each compact set K ⊆ X, x1, x2 ∈ K and ||x1- x2|| ≤ δ, we have
for all t ∈ R, i ∈ N. Let x, y ∈ B, ||x - y|| ≤ δ. Since R(x) ⊆ K0 and R(y) ⊆ K0,
So
Next, we show the following three statements:
(S1) {Γu(t) : u ∈ B} is a relatively compact subset of X for each t ∈ R.
(S2) {Γu : u ∈ B} is equicontinuous.
(S3) {Γu : u ∈ B} is equi-almost-periodic.
(S3) is obvious because B is.
For any ε > 0, let
Since {Γu(t - ε) : u ∈ B} is uniformly bounded in X and T(t, t - ε) is compact, so {Γ ε u(t) : u∈B} is relatively compact in X. Moreover,
So, {Γu(t) : u ∈ B} is a relatively compact subset of X for each t ∈ R. This show (S1).
It remains to prove (S2). Let t″ < t′, t″, t′ ∈ R, u ∈ B,
Moreover,
By (H6), for the given ε > 0, there exists such that if t′, t″ belongs to a same continuity and 0 < t′ - t″ < δ, then
So,
and,
Similarly,
and,
Thus, for u ∈ B, when t′, t″ ∈ R belongs to a same continuity and 0 < t′- t″ < δ,
That is, {Γu: u ∈ B} is equicontinuous and (S2) holds.
Now the conditions of Lemma 2.7 are met, so Γ is compact. By Schauder's point fixed theorem, Γ has a fixed point u ∈ B. That is, (1.3) has a mild piecewise almost periodic solution u(t).
The proof is complete.
Remark 3.2 As we pointed out in Introduction, to get the almost periodic solutions of impulsive differential equations, most people use the Contraction theorem. To be different, we use Schauder's fixed point theorem. This makes proofs difficult. In this case, we impose a stronger condition (A4). To investigate this problem without (A4) and give a easy example will be our next study.
Remark 3.3 Note that the uniform continuity is weaker than the Lipschitz continuity So if the conditions of uniformly continuity of f and I i in (A2) is replaced by
for all x, y ∈ X, η ∈ (0,1), we can also get the mild piecewise almost periodic solution to (1.3) by Theorem 3.1.
In the end, we will use generalized Gronwall-Bellman inequality (Lemma 2.9) to show the asymptotic stability of piecewise almost periodic solutions to (1.3) under the Lipschitz condition.
Theorem 3.4 Assume the conditions of Theorem 3.1 are fulfilled except that (A2) is replaced by (3.3). Assume further that Mη - w < 0, then (1.3) has an asymptotically stable almost periodic solution.
Proof By Remark 3.3, (1.3) has a mild piecewise almost periodic solution x(t),
Let u(t) = u(t, σ, φ) and v(t) = v(t, σ, ψ) be two solutions of Equation (1.3), then
So
Then,
Let ϒ(t) = ewt||u(t) - v(t)||, then
By Lemma 2.9, we have
that is,
This completes the proof.
4 Conclusion
The aim of this article was to give sufficient conditions for existence and asymptotic stability of almost periodic solutions for abstract impulsive differential equations. By taking into consideration the relative compactness for subsets in AP T (R, X), we get almost periodic solutions to impulsive differential equation. In addition, we use generalized Gronwall-Bellman inequality to show the above solution is asymptotically stable.
References
Samoilenko AM, Perestyuk NA: Impulsive differential equations. World Scientific, Singapore; 1995.
Cuevas C, Hernandez E, Rabelo M: The existence of solutions for impulsive neutral functional differential equations. Comput Math Appl 2009, 58(4):744–757.
Cuevas C, N'Guerekata GM, Rabelo M: Mild solutions for impulsive neutral functional differential equations with state-dependent delay. Semigroup Forum 2010, 80: 375–390.
dos Santos JPC, Arjunan M, Cuevas C: Existence results for fractional neutral integro-differential equations with state-dependent delay. Comput Math Appl 2011, 62: 1275–1283.
dos Santos JPC, Cuevas C, de Andrade B: Existence results for a fractional equation with state-dependent delay. Adv Diff Equ 2007. doi:10.1155/2011/642013
Stamov GT, Alzabut JO, Atanasov P, Stamov AG: Almost periodic solutions for an impulsive delay model of price fluctuations in commodity markets. Nonlinear Anal RWA 2011, 12: 3170–3176.
Wang J, Xiang X, Wei W: Linear impulsive periodic system with time-varying generating operators on Banach space. Adv Differ Equ 2007. doi:10.1155/2007/26196
Alzabut JO, Stamov GT, Sermutlu E: On almost periodic solutions for an impulsive delay logarithmic population model. Math Comput Model 2010, 51: 625–631.
Hernandez EM, Tanaka Aki SM, Henriquez H: Global solutions for impulsive abstract partial differential equations. Comput Math Appl 2008, 56: 1206–1215.
Akhmetov MU, Zafer A: Stability of the zero solution of impulsive differential equations by the Lyapunov second method. J Math Anal Appl 2000, 248: 69–82.
Ignatyev AO: On the stability of invariant sets of systems with impulse effect. Nonlinear Anal TMA 2008, 69: 53–72.
Wang J, Xiang X, Peng Y: Periodic solutions of semilinear impulsive periodic system on Banach space. Nonlinear Anal TMA 2009, 71: e1344-e1353.
Liang J, Liu J, Xiao T: Periodic solutions of delay impulsive differential equations. Nonlinear Anal TMA 2011, 74: 6835–6842.
Stamov GT: Asymptotic stability of almost periodic systems of impulsive differential-difference equations. Asymptotic Anal 2001, 27: 1–8.
Yang Z, Xu D: Existence and exponential stability of periodic solution for impulsive delay differential equations and applications. Nonlinear Anal TMA 2006, 64: 130–145.
Sivasankaran S, Arjunan M, Vijayakumar V: Existence of global solutions for second order impulsive abstract partial differential equations. Nonlinear Anal TMA 2011, 74: 6747–6757.
Stamov GT, Alzabut JO: Almost periodic solutions for abstract impulsive differential equations. Nonlinear Anal TMA 2010, 72: 2457–2464.
Henriquez HR, de Andrade B, Rabelo M: Existence of almost periodic solutions for a class of abstract impulsive differential equations. ISRN Math 2011. doi:10.5402/2011/632687
Chang Y, Zhao Z, N'Guerekata GM: A new composition theorem for square-mean almost automorphic functions and applications to stochastic differential equations. Nonlinear Anal TMA 2011, 74: 2210–2219.
Li H, Huang F, Li J: Composition of pseudo almost-periodic functions and semilinear differential equations. J Math Anal Appl 2001, 255: 436–446.
Agarwal RP, de Andrade B, Cuevas C: Weighted pseudo-almost periodic solutions of a class of semilinear fractional differential equations. Nonlinear Anal RWA 2010, 11: 3532–3554.
Agarwal RP, Cuevas C, dos Santos JPC: Analytic resolvent operator and existence results for fractional integro-differential equations. J Abst Diff Equa Appl 2012, 2(2):26–47.
Agarwal RP, de Andrade B, Cuevas C, Henriquez E: Asymptotic periodicity for some classes of integro-differential equations and applications. Adv Math Sci Appl 2011, 21(1):1–31.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, New York; 1983.
Schnaubelt R, Iannelli M, Nagel R, Piazzera S: Asymptotic Behaviour of Parabolic Nonautonomous Evolution Equation. In Lecture Notes in Math. Volume 1855. Springer-Verlag, Berlin; 2004:401–472. Functional Analytic Methods for Evolution Equations
Corduneanu C: Almost Periodic Oscillations and Waves. Springer, New York; 2009.
Wiggins S: Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York; 1990.
Fink AM: Almost Periodic Differential Equations. In Lecture Notes in Mathematics. Volume 377. Springer-Verlag, New York; 1974.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (No. 11071048). The authors would like to thank the referees for carefully reading the manuscript, giving valuable comments and suggestions on the topic of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
JL carried out the main part of this manuscript. CZ participated discussion and corrected the main theorem. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, J., Zhang, C. Existence and stability of almost periodic solutions for impulsive differential equations. Adv Differ Equ 2012, 34 (2012). https://doi.org/10.1186/1687-1847-2012-34
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-34