Attracting and quasi-invariant sets for a class of impulsive stochastic difference equations

Abstract

The aim of this article is to study the attracting and quasi-invariant sets for a class of impulsive stochastic difference equations. By establishing a difference inequality, we obtain the attracting and quasi-invariant sets of systems under consideration. An example is given to illustrate the theory.

Introduction

Difference equations usually appear in the investigation of systems with discrete time or in the numerical solution of systems with continuous time [1]. A lot of difference systems have variable structures subject to stochastic abrupt changes, which may result from abrupt phenomena such as stochastic failures and repairs of the components, changes in the interconnections of subsystems, sudden environment changes, etc. In recent years, the stability investigation of stochastic difference equations has been interesting to many investigators, and various advanced results on this problem have been reported [2–5].

However, besides the stochastic effect, an impulsive effect likewise exists in a wide variety of evolutionary processes in which states are changed abruptly at certain moments of time, involving such fields as medicine and biology, economics, mechanics, electronics and telecommunications. Recently, the asymptotic behaviors of impulsive difference equations have attracted considerable attention. Many interesting results on impulsive effect have been obtained [6–8]. In [9], some stability conditions on impulsive stochastic difference equations are given. As is well known, stability is one of the major problems encountered in applications, and has attracted considerable attention due to its important role in applications. However, under impulsive perturbation, an equilibrium point sometimes does not exist in many physical systems, especially, in non-linear and nonautonomous dynamical systems. Therefore, an interesting subject is to discuss the invariant sets and the attracting sets of impulsive systems. Some significant progress has been made in the techniques and methods of determining the invariant sets and attracting sets for delay difference equations, delay differential equations, and impulsive functional differential equations [10–12]. Unfortunately, the corresponding problems for impulsive stochastic difference equations have not been considered.

Motivated by the above discussion, we here make a first attempt to arrive at results on the invariant sets and attracting sets of impulsive stochastic difference equations.

Model description and preliminaries

Let R ⁿ be the space of n-dimensional real column vectors and R ₊ = [0, +∞). N[a, b] {a, a + 1,..., b}, where a < b and a, b are integral numbers. C denotes the set of all functions ϕ : N[-h, 0] → R ⁿ , h is a nonnegative integer. For any φ ∈ C, we define . Z denotes the integer set. Let {Ω, P, Σ} be a basic probability space, Σ _i-1⊂ Σ _i ⊂ Σ, i ∈ Z be a sequence of Σ-algebras E be the mathematical expectation, ξ₀, ξ₁,... be a sequence of mutually independent random variables, ξ _i ∈ R, ξ _i be Σ _i -adapted and independent on. Σ _i-1, Eξ _i = 0, , i ∈ Z. Let C _Ω denote the family of C-valued random variables on {Ω, P, Σ}.

In this article, we mainly consider the following impulsive stochastic difference equations

(1)

with initial condition

where F, G : Z × R ^{h+ 1}→ R, H _i : R → R. φ (i) ∈ C _Ω. The fixed moments of time i _k ∈ Z, and satisfy . x _i is an element of C _Ω defined by x _i = x (i + s), s ∈ N [-h, 0].

Throughout this article, we assume that for any φ (i) ∈ C _Ω, there exists at least one solution of (1), which is denoted by x(i, 0, φ) or x _i (0, φ) (simply x(i) and x _i if no confusion should occur).

Definition 2.1. The set S ⊂ C _Ω is called a quasi-invariant set of (1), if there exists a constant k such that for any initial value φ ∈ S, the solution kx _i (0, φ) ∈ S, i ∈ Z. Especially, if k = 1, S is called a invariant set.

Dedinition 2.2. The set S ⊂ C _Ω is called a global attracting set of (1), if for any initial value φ ∈ C _Ω, the solution x _i (0, φ) satisfies

where

where ρ(·,·) is any distance in C _Ω.

Definition 2.3. The zero solution of Equation (1) is called mean square exponential stable if there are positive constants λ and M such that for any initial condition φ ∈ C _Ω,

Here λ is called the exponential convergence rate. Of course, conditions are needed to ensure that the zero function is a solution of (1).

Based on discrete Halanay inequality [13] and its extension [9], we develop the following difference in-equality with the impulsive initial condition.

Lemma 2.1. Suppose c _j (i) ∈ R ₊, i ∈ Z, j ∈ N[0,h], and b > 0. Let u(i) be a sequence of real numbers satisfying the following difference inequality:

(2)

• (a) Then

  

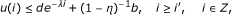  (3)

provided that the initial condition satisfies

(4)

where i' ∈ Z, d ∈ R ₊ and λ satisfies

(5)

• (b) Then

  

  (6)

provided the initial condition

(7)

where i' ∈ Z and γ ≥ 1.

Proof. (a) Since η < 1, there exists a constant λ satisfying the inequality (5). Then,

(8)

If (3) is not true, then there must be a positive integral number i* ≥ i' such that

(9)

By (2), (8), and (9), we have

which contradicts the first inequality of (9). So (3) holds. The proof of part (a) is complete. (b) If (6) is not true, then there must be a positive integral number i* ≥ i' such that

(10)

By (2), (10), we have

which contradicts the first inequality of (10). So (6) holds. The proof of part (b) is complete.

Main results

To establish the main results of system (1), we will employ the following assumptions. (A₁) For any i ∈ Z, there exist positive constants a _j (i), b _j (i), J ₁ and J ₂ such that

(A₂) , where and .

(A₃) There exist constants d _k ≥ 1 such that

(A₄) There exists constant α ≥ 0 such that

where i ₀ = 0 and λ* satisfies

and

(A₅) There exist nonnegative constants d _k ≤ 1 such that

(A₆) For any i ∈ Z, there exist positive constants a _j (i) and b _j (i) such that

(A₇) , where and .

Theorem 3.1. If (A₁)- (A₄) hold, then S = {ϕ ∈ C _Ω|E||ϕ||² ≤e ^σ(1-μ)^-1 J} is a global attracting set of (1), where .

Proof. From (1), Condition (A₁), (a + b)² ≤ 2 (a ² + b ²) and the Hölder inequality, we have

(11)

From condition (A₂), we obtain

(12)

For the initial conditions x(s) = φ(s), s ∈ N[-h, 0], where φ ∈C _Ω, we have a positive constant K such that

(13)

Then, all the conditions of the part (a) of Lemma 2.1 are satisfied by (11)-(13). So, we can obtain

Suppose for all q = 1, 2,..., k, the inequalities

(14)

hold, where d ₀ = 1 and i ₀ = 0. Then from condition (A₃) and (14), we have

This, together with (14) and d _k ≥ 1, k = 1, 2,..., leads to

(15)

It follows from (11), (12), (15), and the part (a) of Lemma 2.1 that

yielding, together with (14) that

By mathematical induction, we can conclude that

(16)

Noticing that and by condition (A₄), we can use (16) to conclude that

This implies that the conclusion holds and the proof is complete.

Theorem 3.2. If (A₁)-(A₄) hold, then S = {ϕ ∈ C _Ω |E||ϕ||² ≤ γ (1-μ)^-1 J, γ ≥ 1}is a quasi-invariant set of (1).

Proof. For the initial conditions x(s) = φ(s), s ∈ N [-h, 0], where φ ∈ S we have

(17)

By (17) and the part (b) of Lemma 2.1, we have

Suppose for all q = 1, 2,..., k, the inequalities

(18)

hold, where d ₀ = 1 and i ₀ = 0. Then from condition (A₃) and (18), we have

This, together with (18) and d _k ≥ 1, k = 1, 2,..., leads to

(19)

It follows from (19) and the part (b) of Lemma 2.1 that

yielding, together with (18), that

By mathematical induction, we can conclude that

(20)

Noticing that by condition (A₄), we can use (20) to conclude that

This implies that the conclusion holds and the proof is complete.

Theorem 3.3. If (A₁)-(A₂) and (A₅) hold, then S = {ϕ ∈ C _Ω |E||ϕ||² ≤ γ (1-μ)^-1 J} is a invariant set and also a global attracting set of (1).

Proof. Since d _k ≤ 1, a direct calculation shows that α* = 0 and σ = 0 in Theorems 3.1 and 3.2. It follows from Theorem 3.1 the set S is a global attracting set of (1). It follows from Theorem 3.2 the set S is a invariant set of (1).

If , k = 1,2,..., the system (1) reduce to the following system without impulses

(21)

with initial condition

By Theorem 3.3, we can obtain the following result.

Corollary 3.1. If (A₁) and (A2) hold, then S = {ϕ ∈ C _Ω|E||ϕ||² ≤ (1-μ)^-1 J} is a invariant set and also a global attracting set of (21).

We easily observe x(i) = 0 is a solution of (1) from (A₃) and (A₆). In the following, we give the attractivity of the zero solution and the proof is similar to that of Theorem 3.1.

Theorem 3.4. If (A₃), (A₄), (A₆), and (A₇) hold, then the zero solution of Equation (1) is mean square exponential stable and the exponential convergence rate is equal to λ* - α*.

Example

In this section, we shall discuss an example in order to illustrate the effectiveness of our results. Example 4.1. Consider the following impulsive stochastic difference equation:

(22)

where i _k = i _k-1+ 5k. Thus,

yielding

So, the parameters of conditions (A₁), (A₂), and (A₃) are as follows:

Since , we can get α* = 0.016 and . Moreover, . Then the condition (A₄) is satisfied. So, by Theorem 3.1, we can get that

is a global attracting set of (22). By Theorem 3.2, we can get that S is a quasi-invariant set of (22).

Conclusion

The aim of this article is to study the attracting and quasi-invariant sets for a class of impulsive stochastic difference equations. By establishing a difference inequality, we obtain the attracting and quasi-invariant sets of systems under consideration. As pointed out by the reviewer, when F and G do not depend on i, the solutions of (1) are time-homogeneous Markovian in character except that there is an impulse at predetermined times i ₁, i ₂, i ₃.... For time-homogeneous Markov chains there is a well-established stability theory most eloquently summarized by Meyn and Tweedie [14]. We will explore the relationship between our work and the established theory of stochastic stability for Markov chains in the next article.