- Research
- Open access
- Published:
Superstability of generalized cauchy functional equations
Advances in Difference Equations volume 2011, Article number: 23 (2011)
Abstract
In this paper, we consider the stability of generalized Cauchy functional equations such as

Especially interesting is that such equations have the Hyers-Ulam stability or superstability whether g is identically one or not.
2000 Mathematics Subject Classification: 39B52, 39B82.
1. Introduction
The most famous functional equations are the following Cauchy functional equations:




Usually, the solutions of (1.1)-(1.4) are called additive, exponential, logarithmic and multiplicative, respectively. Many authors have been interested in the general solutions and the stability problems of (1.1)-(1.4) (see [1–5]).
The stability problems of functional equations go back to 1940 when Ulam [6] proposed the following question:
Let f be a mapping from a group G 1 to a metric group G 2 with metric d(·,·) such that

Then does there exist a group homomorphism L : G 1 → G 2 and δ ε > 0 such that

for all × ∈ G 1 ?
The case of (1.1) was solved by Hyers [7]. He proved that if f is a function between Banach spaces satisfying ||f(x+y) - f(x) - f(y)|| ≤ ε for some fixed ε > 0, then there exists a unique additive mapping A such that ||f(x) - A(x)|| ≤ ε. From these historical backgrounds, the functional equation

is said to have the Hyers-Ulam stability if for an approximate solution φ s such that

for some fixed constant ε > 0 there exists a solution φ of (1.5) such that

for some positive constant ≤ δ ε .
During the last decades, Hyers-Ulam stability of various functional equations has been extensively studied by a number of authors (see [3–5, 8–10]). Especially, Forti [11] proved the Hyers-Ulam stability of (1.3). The stability of (1.2) was proved by Baker, Lawrence and Zorzitto [12]. They proved that if f is a function satisfying |f(x + y) - f(x)f(y)| ≤ ε for some fixed ε > 0 then f is either bounded or else f(x+y) = f(x)f(y). In order to distinguish this phenomenon from the Hyers-Ulam stability, we call this phenomenon superstability. Generalizing results as in [12], Baker [13] proved that the superstability for (1.4) does also hold.
In this paper, we consider the stability of generalized Cauchy functional equations such as


We say that (1.6) and (1.7) are generalized Cauchy functional equations because these are reduced the Cauchy functional equations if g is identically one. It is easily checked that the general solutions of (1.6) are additive or exponential whether g is identically one or not. From this point of view, we can expect that (1.6) has the Hyers-Ulam stability or superstability due to the conditions of g. Actually, if g is identically one in (1.6), then Hyers-Ulam stability holds [7]. On the other hand, if g is not identically one in (1.6), then we shall see in Section 2 that superstability holds in this case. That is, f and g are either bounded or else f(x + y) = f(x)g(y) + f(y).
Analogously, it is easy to see that the general solutions of (1.7) are logarithmic or multiplicative whether g is identically one or not. If g is identically one in (1.7), then this case is exactly the same as in [11]. And hence Hyers-Ulam stability holds in this case. We shall prove that if g is not identically one in (1.7), then f and g are either bounded or else f(xy) = f(x)g(y)+f(y).
2. Stability of (1.6) and (1.7)
We first consider the stability of (1.6). The general solutions of (1.6) are given by

where A is an additive mapping, E is an exponential mapping and a is an arbitrary nonzero constant. For the proof we refer to [[14], Lemma 1]. Although (1.6) is slightly different from (1.1), the general solutions of (1.6) are related to (1.2) rather than (1.1) if g is not identically one. The stability result in the case of g ≡ 1 in (1.6) is well known as follows.
Theorem 2.1. [4, 7] Let E 1 be a normed vector space and E 2 a Banach space. Suppose that f : E 1 → E 2 satisfies the inequality

for all x, y in E 1, where ε > 0 is a constant. Then the limit

exists for all × in E 1 and A : E 1 → E 2 is a unique additive mapping satisfying

for all × in E 1.
According to the above result, we know that Hyers-Ulam stability holds if g is identically one. Thus, it suffices to show the case g ≢ 1. Especially interesting is that superstability holds if g is not identically one as follows.
Theorem 2.2. Let V be a vector space and let f, g : V →≤ be complex valued functions with g ≢ 1. Suppose that f and g satisfy the inequality

Then, one of the following conditions holds:
-
(i)
If f ≡ 0, then g is arbitrary;
-
(ii)
If f(≢ 0) is bounded or f(0) ≠ 0 , then g is also bounded;
-
(iii)
If f is unbounded, then f(0) = 0, g is also unbounded and f(x+y) = f(x)g(y) + f(y) for all x, y ∈ V.
Proof. (i) If f ≡ 0, then we easily see that g is arbitrary.
-
(ii)
Suppose that f is bounded and f ≢ 0. Then, there exists a constant M > 0 such that |f(x)| ≤ M for all x ∈ V. From (2.1), it follows that
 (2.2)
(2.2)
for all x, y ∈ V. Since f ≢ ≡ 0, there exists a point x 0 such that f(x 0) ≠ 0. Putting x = x 0 in (2.2) and dividing the result by |f(x 0)| we have

for all y ∈ V. This shows that g is bounded.
Now assume that f(0) ≠ 0. Putting x = 0 in (2.1) yields

for all y ∈ V. We see that g is bounded, since f(0) ≠ 0.
-
(iii)
Finally, we are going to prove the case that f is unbounded. Since f is unbounded, we can take a sequence {x n } such that |f(x n )| → ∞. Putting x = x n in (2.1) and dividing both sides by |f(x n )| we have
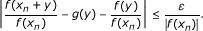
Letting n → ∞ we obtain

Substituting x = x + x n in (2.1) gives

Dividing both sides by |f(x n )| and then letting n → ∞ we have

for all x, y ∈ V. We observe that g is also unbounded. If g ≡ 0, then from (2.1) we have

for all x, y ∈ V. This shows that f is bounded and hence this reduces a contradiction. Since g satisfies (2.3) with g ≢ 0 and g ≢ 1, we conclude that g is unbounded. Choose a sequence {y n } such that |g(y n )| → ∞. Putting y = y n in (2.1) and dividing both sides by |g(y n )| we have

Letting n → ∞ yields

We note that f(0) = 0. Substituting y = y + y n in (2.1) and using (2.3) we obtain

Dividing both sides in the above inequality by |g(y n )| and then letting n → ∞ we have

This completes the proof. □
Analogously, we are going to consider the stability of (1.7). The general solutions of (1.7) are given by

where L is a logarithmic mapping, M is a multiplicative mapping and b is an arbitrary nonzero constant. In case of g ≡ 1, the stability result is well known as follows:
Theorem 2.3. [5, 11] Let S be a semigroup and Y a Banach space. Further, let f : S → Y be a mapping satisfying

for all x, y in S. Then the limit

exists for all × in S and L : S → Y is a unique mapping satisfying

and

for all × in S. If S is commutative, then L is logarithmic.
For that reason, we only consider the case g ≢ 1.
Theorem 2.4. Let V be a vector space and let f, g : V → ≤ be complex valued functions with g ≢ 1. Suppose that f and g satisfy the inequality

Then, one of the following conditions holds:
-
(i)
If f ≡ 0, then g is arbitrary;
-
(ii)
If f(≢ 0) is bounded or f(1) ≠ 0 , then g is also bounded;
-
(iii)
If f is unbounded, then f(1) = 0, g is also unbounded and f(xy) = f(x)g(y) + f(y) for all x, y ∈ V.
Proof. (i) If f ≡ 0, then from (2.4) we see that g is arbitrary.
-
(ii)
Suppose that f is bounded and f ≢ 0. Then, there exists a constant N > 0 such that |f(x)| ≤ N for all x ∈ V. It follows from (2.4) that we calculate
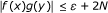
for all x, y ∈ V. Since f ≢0, we see that g is bounded.
Assume that f(1) ≠ 0. Putting x = 1 in (2.4) we have g is bounded.
-
(iii)
Now we prove the case that f is unbounded. Since f is unbounded, we can take a sequence {x n } such that |f(x n )| → ∞. Putting x = x n in (2.4) and dividing both sides by |f(x n )| we have

Letting n → ∞ we obtain

Replacing x by xx n in (2.4) yields

Dividing both sides by |f(x n )| and then letting n → ∞ we have

for all x, y ∈ V. If g ≡ 0, then from (2.4) we have

for all x, y ∈ V. Putting y = 1 in (2.6) we see that f is bounded. This reduces a contradiction. Since g satisfies (2.5) with g ≢ 0 and g ≢ 1, we can choose a sequence {y n } such that |g(y n )| → ∞. Putting y = y n in (2.4) and dividing the result by |g(y n )| we have

Letting n → ∞ gives

Putting x = 1 yields f(1) = 0. Replacing y by yy n in (2.4) and using (2.5) we have

Dividing both sides by |g(y n )| and letting n → ∞ we obtain

This completes the proof. □
References
Aczél J: Lectures on Functional Equations and Their Applications. Academic Press, New York; 1966.
Aczél J, Dhombres J: Functional Equations in Several Variables. Cambridge University Press, Cambridge; 1989.
Czerwik S: Functional Equations and Inequalities in Several Variables. World Scientific Publishing Co., Inc., River Edge, NJ; 2002.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables. Birkhäuser, Basel; 1998.
Kannappan Pl: Functional Equations and Inequalities with Applications. Springer; 2009.
Ulam SM: Problems in Mordern Mathematics. Wiley, New York; 1964.
Hyers DH: On the stability of the linear functional equation. Proc Natl Acad Sci USA 1941, 27: 222–224. 10.1073/pnas.27.4.222
Chung J: Stability of a Jensen type logarithmic functional equation on restricted domains and its asymptotic behaviors. Adv Diff Equ 2010, 2010: 13. Art. ID 432796
Moghimi MB, Najati A, Park C: A fixed point approach to the stability of a quadratic functional equation in C *-algebras. Adv Diff Equ 2009, 2009: 10. Art. ID 256165
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proc Am Math Soc 1978, 72: 297–300. 10.1090/S0002-9939-1978-0507327-1
Forti GL: The stability of homomorphisms and amenability, with applications to functional equations. Abh Math Sem Univ Hamburg 1987, 57: 215–226. 10.1007/BF02941612
Baker J, Lawrence J, Zorzitto F: The stability of the equation f ( x + y ) = f ( x ) f ( y ). Proc Am Math Soc 1979, 74: 242–246.
Baker JA: The stability of the cosine equation. Proc Am Math Soc 1980, 80: 411–416. 10.1090/S0002-9939-1980-0580995-3
Kannappan Pl, Sahoo PK: On generalizations of the Pompeiu functional equation. Int J Math Math Sci 1998, 21: 117–124. 10.1155/S0161171298000155
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No.2011-0000092).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
YL carried out the main part of this manuscript. SC participated discussion and corrected the main theorem. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lee, YS., Chung, SY. Superstability of generalized cauchy functional equations. Adv Differ Equ 2011, 23 (2011). https://doi.org/10.1186/1687-1847-2011-23
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2011-23