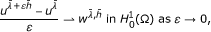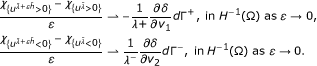- Research
- Open access
- Published:
Perturbation formula for the two-phase membrane problem
Advances in Difference Equations volume 2011, Article number: 19 (2011)
Abstract
A perturbation formula for the two-phase membrane problem is considered. We perturb the data in the right-hand side of the two-phase equation. The stability of the solution and the free boundary with respect to perturbation in the coefficients and boundary value is shown. Furthermore, continuity and differentiability of the solution with respect to the coefficients are proved.
Introduction
Let λ
± :Ω → ℝ be non-negative Lipschitz continuous functions, where Ω is a bounded open subset of ℝ n with smooth boundary. Assume further that g ∈ W
1,2(Ω)∩ L
∞(Ω) and g changes sign on ∂Ω. Let  . Consider the functional
. Consider the functional

which is convex, weakly lower semi-continuous and hence attains its infimum at some point u ∈ K. The Euler-Lagrange equation corresponding to the minimizer u is given by Weiss [1] and is called the two-phase membrane problem:

where χ A denotes the characteristic function of the set A, and

is called the free boundary. The free boundary consists of two parts:

and

By Ω+(u) and Ω - (u) we denote the sets {x ∈ Ω: u(x) > 0} and {x ∈ Ω: u(x) < 0}, respectively. Also, Λ(u) denotes the set {x ∈ Ω: u(x) = 0}.
The regularity of the solution, the Hausdorff dimension and the regularity of the free boundary are discussed in [2–5]. In [5], on the basis of the monotonicity formula due to Alt, Caffarelli, and Friedman, the boundedness of the second-order derivatives D 2 u of solutions to the two-phase membrane problem is proved. Moreover, in [3], a complete characterization of the global two-phase solution satisfying a quadratic growth at a two-phase free boundary point and at infinity is given. In [4] it has been shown that if λ + and λ - are Lipschitz, then, in two dimensions, the free boundary in a neighborhood of each branch point is the union of two C 1-graphs. Also, in higher dimensions, the free boundary has finite (n - 1)-dimensional Hausdorff measure. Numerical approximation for the two-phase problem is discussed in [6].
In this article, by perturbation we mean the perturbation of the coefficients λ + and λ - and the perturbation of the boundary values g. The case of the one phase obstacle problem has been studied in [7].
For given (λ
+,λ
- ) ∈ C
0,1(Ω) × C
0,1(Ω), Equation 1.2 has a unique solution  for
for
-
1
< p < ∞ (see [8]). Define the map
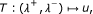 (1.3)
(1.3)
where u is the solution of (1.2) corresponding to the coefficients λ + and λ - . The main results in this paper are the following:
-
1.
The stability of solution with respect to boundary value and coefficients is shown.
-
2.
Let
 . By
. By 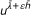 , we mean the solution of problem (1.2) with coefficients (λ + + εh 1) and (λ - + εh 2). If we Consider the map T : (λ +, λ
- ) ↦ u, for given parameters λ + and λ + and a fixed Dirichlet condition, then the Gateaux derivative of this map is characterized in
, we mean the solution of problem (1.2) with coefficients (λ + + εh 1) and (λ - + εh 2). If we Consider the map T : (λ +, λ
- ) ↦ u, for given parameters λ + and λ + and a fixed Dirichlet condition, then the Gateaux derivative of this map is characterized in 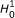 . More precisely, it is shown in Theorem 3.4 that
. More precisely, it is shown in Theorem 3.4 that 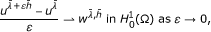
where

-
3.
(Theorem 3.5) Assuming that all free boundary points are one-phase points (points such that ∇u = 0), a stability result for the free boundary in the flavor of [7] is proved which says that
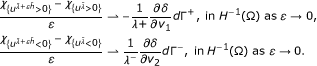
Were Γ± = ∂ {±u(x) > 0} ∩ Ω. The function δ is constructed as a solution of certain Dirichlet problem in  . The vector v
1 stands for the exterior unit normal vector to
. The vector v
1 stands for the exterior unit normal vector to  .
.
The structure of article is organized as follows. In the next section, stability of solution with respect to boundary value and coefficients is studied. In Section 3, we prove that the map T is Lipschitz continuous (Theorem 3.1) and differentiable (Theorem 3.4).
Preliminary analysis and stability results
In this section, we state some lemmas which have been proved in the case of one-phase obstacle problem (see [9]). The following proposition shows the stability in L ∞-norm. In what follows, we will denote by B r (x 0) the ball of radius r centered at x 0 and, for simplicity, we use the notation B r = B r (0).
Proposition 2.1. Let u i for i = 1, 2 be the solution of the following problem

If g 1 ≤ g 2 ≤ g 1 + ε, then u 1 ≤ u 2 ≤ u 1 + ε. In particular,

Proof. First, we show that u
1 ≤ u
2. Denote  ; then, for all
; then, for all  the following inequalities hold.
the following inequalities hold.

and

These inequalities imply that

which shows that

One can see that on the boundary of  , the following holds:
, the following holds:

Note that by assumptions on g
1 and g
2, the inequality u
1 - u
2 ≤ 0 will hold on the  . Thus, we have,
. Thus, we have,

By maximum principle, we obtain that

which is impossible. Therefore,  .
.
Let u 3 be the solution to the following problem:

An analysis similar to the one above shows that if v = u 1 + ε - u 3, then v ≥ 0, which implies

□
Lemma 2.2. Assume that
 . Let u be a solution to
. Let u be a solution to

and let u ε solve

with u = u ε = g on ∂ B 1. Then

Proof. Let ε > 0,; we will show that u ε ≤ u. Set D = {x ∈ B 1 : u ε (x) > u(x)}. If u ε ≤ 0, on D, then u < 0 on D and Δu = - λ - ≤ - (λ - - ε) ≤ Δu ε : On the other hand, if u ε > 0; then Δu ε = λ + + ε ≥ Δu. Therefore, Δu ε ≥ Δu and, by maximum principle, D = ∅.
Now we claim that also u + εv ≤ u ε in B 1, where v is the solution to Δv = 1 with zero Dirichlet boundary data in B 1. Assume that

Note that v(x) ≤ 0 in B 1, and so we have

Then, for all  , the following inequalities hold:
, the following inequalities hold:

and

In  , we have
, we have

Therefore, we have

This shows that u + εv ≤ u
ε in  , which is impossible. Since
, which is impossible. Since

this implies that u
ε ≥ -Cε + u. Note that in the case when ε < 0, with the assumption  one can prove that
one can prove that

□
Remark 1. An analysis similar to Lemma 2.2 shows that if the coefficients λ ± be perturbed by ±ε, then |u ε - u| ≤ Cε.
Remark 2. The proofs of Proposition 2.1 and Lemma 2.2 show that if u and v solve the following problems, respectively:

and

with  , then u ≥ v. In particular,
, then u ≥ v. In particular,

Theorem 2.3. Let u
k
be a sequence of minimizer to (1.1), respectively with data g
k
and
 , such that
, such that

and

Then,

where u is the minimizer of (1.1) with data g and potential λ ±.
Proof. First, one can see that g is an admissible boundary data, i.e., g changes sign on the boundary by the strong convergence of g
k
in  . We denote by u* the solution to minimization problem (1.1) with data g and λ
±. Consider the minimum levels c
k
= I
k
(u
k
) and c* = I(u*). Also the convergence of the boundary traces g
k
and of the
. We denote by u* the solution to minimization problem (1.1) with data g and λ
±. Consider the minimum levels c
k
= I
k
(u
k
) and c* = I(u*). Also the convergence of the boundary traces g
k
and of the  , ensures a bound on the sequence c
k
. Since the sequence of functionals {I
k
} is uniformly coercive, from the fact that I
k
(u
k
) ≤ C, we infer a bound on the sequence
, ensures a bound on the sequence c
k
. Since the sequence of functionals {I
k
} is uniformly coercive, from the fact that I
k
(u
k
) ≤ C, we infer a bound on the sequence  ; therefore, we can assume, up to a subsequence, that
; therefore, we can assume, up to a subsequence, that

Furthermore, by the weak continuity of the trace operator, we obtain

The weak lower semi-continuity of the norm implies

and we also have

Note that the level

is not necessarily a minimum, but, by the previous discussion it satisfies the inequalities

We shall prove that c 0 = c*. Suppose, by contradiction, that c* < c 0. Consider the harmonic extensions (denoted with the same notations) on Ω of g i 's and of g and introduce

Then, by construction

We define w k = u* + h k , and observe that w k |∂Ω = g k . Moreover, by (1.7),

Hence, it follows from the definition of c k that

On the other hand, (1.8) gives

which implies that c* ≥ c 0. Finally, from the equality of the minima c 0 = c = c*, we also deduce the strong convergence of u k in H 1(Ω). □
Perturbation formula for the free boundary
In this section, we prove the continuity and differentiability of the map T. The case of one-phase obstacle problem was studied by Stojanovic [7].
Theorem 3.1. Assume λ
+, λ
- ∈ L
p (Ω) for
 . The map (λ
+, λ
- ) ↦ u is Lipschitz continuous in the following sense. If u
i
for i = 1, 2 solves
. The map (λ
+, λ
- ) ↦ u is Lipschitz continuous in the following sense. If u
i
for i = 1, 2 solves

then

and for


We first prove the following lemma:
Lemma 3.2. If

then

where δ > 0,  solves
solves

Moreover, the same argument can be applied with

Proof. Let


Then, by the same proof as in the first part of Lemma 2.2, one gets

where u
3 and u
4 solve Equation 1.2 with coefficients  ,
,  , respectively. Relation (1.10) gives
, respectively. Relation (1.10) gives

Also, by the choice of  , we have
, we have

We will show that

First, note that

Therefore,

Rearranging the above terms gives

Multiplying by (u 4 -(u 3 + δ))+ and integrating by parts gives

Then,

It follows that

Note that

Then, we have

However,

In the last equation, we have used (1.16).
□
Thus we completed the proof of Theorem 3.1.
Proof of Theorem 3.1. By elliptic regularity and Lemma 3.2, we have

and, consequently, the Sobolev embedding  for
for  , implies
, implies

Therefore,

Now if we assume  , then it will follows that |u
2 - u
1| < δ. To complete the proof, assume that
, then it will follows that |u
2 - u
1| < δ. To complete the proof, assume that

Set  . Then, we have
. Then, we have

and

By Equation 1.11, we obtain

□
The proof of Theorem 3.4 uses the following theorem, proved by I. Blank in [9].
Theorem 3.3. (Linear Stability of the Free Boundary in the one phase case). Suppose that the free boundary is locally uniformly C 1, α regular in B 1. Let w, w ε be the solutions of the following one-phase problems, respectively,

and

Then, for ε small enough, we have

Remark 3. The analogue of Theorem 3.3 can be proved for the two-phase membrane problem in the following cases:
-
(1)
When all the points are regular one-phase points (cf. Theorem 3.3).
-
(2)
When all the points are two-phase points with |∇u| = 0 (branching points).
-
(3)
When |∇u| is uniformly bounded from below (cf. Estimate 1.19).
Although we could not prove this theorem for the two-phase case in general, there are grounds, however, to suggest that it holds true in this case as well.
The proof of part (3) is as follows. Suppose ε > 0, h
1
> 0, h
2
< 0 and  . Then Lemma 2.2 implies that
. Then Lemma 2.2 implies that

Also,  for x ∈ Ω+ ∩ B
r
where r is small enough, which gives
for x ∈ Ω+ ∩ B
r
where r is small enough, which gives

Thus,  is positive provided that
is positive provided that  , which shows
, which shows

Now we shall prove that the map  is differentiable in the following sense:
is differentiable in the following sense:
Theorem 3.4. The mapping

defined by u = T(λ
+, λ
-) is differentiable. Furthermore, if
 . Then, there exists
. Then, there exists
 , such that
, such that

where

In Equation
1.20,  denotes the (n - 1)-dimensional Hausdorff measure.
denotes the (n - 1)-dimensional Hausdorff measure.
Proof. We have

and

Therefor,

We multiply both sides of (1.21) by  and integrate by parts and we obtain
and integrate by parts and we obtain

Note that

and

Therefore,

The Hölder inequality implies

Moreover, by the Poincaré inequality, we have

From (1.22), the weak convergence to a limit, denoted by  , follows (for a subsequence). Here, we show that
, follows (for a subsequence). Here, we show that  satisfies (1.20). Multiply (1.21) by a test function ϕ, where ϕ has compact support in
satisfies (1.20). Multiply (1.21) by a test function ϕ, where ϕ has compact support in  , and then divide by ε,
, and then divide by ε,

Assume that d is the distance between supp(ϕ) and  . If
. If  , then, (since
, then, (since  ) for ε small enough, we have
) for ε small enough, we have

and so  . This means that, for each ϕ, one can chose ε small enough such that
. This means that, for each ϕ, one can chose ε small enough such that

In particular, passing to the limit in (1.23), we obtain that in the set  , equation
, equation

holds. Similarly, in the set  , one has
, one has

Now let x
0 be a one-phase regular point for  and
and  where x
ε
has minimal distance to x
0.
where x
ε
has minimal distance to x
0.
Assumption In what follows, we assume that the estimate (1.18) in Theorem 3.3 also holds for one-phase points in our case. A straightforward calculation gives

which shows that  at one-phase regular points.
at one-phase regular points.
To complete the proof, let us assume that  . Let ν denote the normal to the free boundary
. Let ν denote the normal to the free boundary  at x
0, that is
at x
0, that is  . Assume that B
r
(x
0) is a ball centered at x
0 where r is small enough. Since ∇u(x
0) ≠ 0, then
. Assume that B
r
(x
0) is a ball centered at x
0 where r is small enough. Since ∇u(x
0) ≠ 0, then  can be represented as (x', f(x')) where f is a C
1, αgraph. We have
can be represented as (x', f(x')) where f is a C
1, αgraph. We have

Let Ω
ε
be the region between  and
and  . From (1.21) we obtain
. From (1.21) we obtain

The term  converges weakly as ε → 0, to a measure μ with support on Γ"(u). For any ball B
r
(x
0) with x
0 ∈ Γ"(u), set
converges weakly as ε → 0, to a measure μ with support on Γ"(u). For any ball B
r
(x
0) with x
0 ∈ Γ"(u), set

Estimate (1.19) shows that μ is a finite measure, since

We want to prove that

Then, μ can be written as (see [10], Chapter I)

Let d be the distance of x
0 to  in direction of v, using Taylor expansion, we get
in direction of v, using Taylor expansion, we get

In order to show (1.25), we have

where  is the measure of
is the measure of  . In addition, we have
. In addition, we have

Therefore,

We deduce that,  satisfies (1.20).
satisfies (1.20).
□
Remark 4. If for all free boundary points ∇u = 0, which means that Γ(u) = Γ'(u), then

where  is the unique solution of the elliptic equation
is the unique solution of the elliptic equation

Remark 5. Consider the following two-phase problem in dimension one (n = 1), where λ 1, λ 2 are constants.

Straightforward calculations show that if  , then the set {x ∈ Ω: u(x) = 0} has a positive measure. In this setting, an interesting question is which conditions in higher dimensions will imply that the zero set has positive measure in B
1.
, then the set {x ∈ Ω: u(x) = 0} has a positive measure. In this setting, an interesting question is which conditions in higher dimensions will imply that the zero set has positive measure in B
1.
Example 1 Let  ,
,  . Consider the equation
. Consider the equation

One can obtain

Consequently, one computes

By Weiss [1], we know that the Hausdorff dimension of Γ = ∂{u > 0} ∪ ∂{u < 0} is less than or equal to n - 1 and by Edquist et al. [2] the regularity of the free boundary is C
1. Let d Γ denote the measure  ; the restriction of the (n - 1)-dimensional Hausdorff measure
; the restriction of the (n - 1)-dimensional Hausdorff measure  on the set Γ. Moreover, let v
1 be the unit normal exterior to ∂{u > 0} and v
2 be the unit normal to ∂{u < 0} exterior to {u < 0}.
on the set Γ. Moreover, let v
1 be the unit normal exterior to ∂{u > 0} and v
2 be the unit normal to ∂{u < 0} exterior to {u < 0}.
Theorem 3.5. Assume that the free boundary points are one-phase points, and let δ be the same as defined in Remark 4. Then, we have

weakly in H -1(Ω) as ε → 0. In addition

Proof. To begin with, observe that

Then, for a test function  one obtains
one obtains

The left-hand side of Equation 1.27 is

Let ε → 0, in (1.27); then, by the notations introduced in Remark 4, one has

Integrating by parts gives

In the view of Remark 4, we have

Finally, we conclude that

and

References
Weiss GS: An obstacle-problem-like equation with two phases: pointwise regularity of the solution and an estimate of the Hausdorff dimension of the free boundary. Interfaces Free Bound 2001, 3: 121–128.
Edquist A, Lindgren E, Shahgholian H: On the two-phase obstacle problem with coefficents below the lipschitz threshold. Annales de l'Institut Henri Poincare (C) Non Linear Anal 2009, 26: 2359–2372. 10.1016/j.anihpc.2009.03.006
Shahgholian H, Uraltseva N, Weiss GS: Global solutions of an obstacle-problem-like equation with two phases. Monatsh. Math 2004, 142: 27–34. 10.1007/s00605-004-0235-6
Shahgholian H, Weiss GS: The two-phase membrane problem--an intersection-comparison approach to the regularity at branch points. Adv Math 2006, 205: 487–503. 10.1016/j.aim.2005.07.015
Uraltseva N: Two-phase obstacle problem, function theory and phase transitions. J Math Sci 2001, 106: 3073–3077. 10.1023/A:1011327823592
Bozorgnia F: Numerical solution of two-phase membrane problem. Appl Numer Math 2011, 61: 92–107. 10.1016/j.apnum.2010.08.007
Stojanovic S: Perturbation formula for regular free boundaries in elliptic and parabolic obstacle problems. SIAM J Control Optim 1997, 35: 2086–2100. 10.1137/S0363012995282796
Gilbarg D, Trudinger N: Elliptic Partial Differential Equations of Second Order. Springer, New York; 1983.
Blank I: Sharp results for the regularity and stability of the free boundary in the obstacle problem. Indiana Univ Math J 2001,50(3):1077–1112.
Evans LC, Gariepy R: Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton; 1992.
Acknowledgements
The author thanks Henrik Shahgholian for initiating this work and for useful suggestions. Moreover, the author would like to express his great sense of gratitude to the referees for carefully reading the article and coming with many helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bozorgnia, F. Perturbation formula for the two-phase membrane problem. Adv Differ Equ 2011, 19 (2011). https://doi.org/10.1186/1687-1847-2011-19
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2011-19
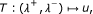
 . By
. By 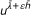 , we mean the solution of problem (1.2) with coefficients (λ + + εh 1) and (λ - + εh 2). If we Consider the map T : (λ +, λ
- )
, we mean the solution of problem (1.2) with coefficients (λ + + εh 1) and (λ - + εh 2). If we Consider the map T : (λ +, λ
- ) 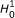 . More precisely, it is shown in Theorem 3.4 that
. More precisely, it is shown in Theorem 3.4 that