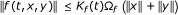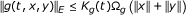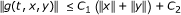- Research
- Open access
- Published:
Mild solutions for a problem involving fractional derivatives in the nonlinearity and in the non-local conditions
Advances in Difference Equations volume 2011, Article number: 18 (2011)
Abstract
A second-order abstract problem of neutral type with derivatives of non-integer order in the nonlinearity as well as in the nonlocal conditions is investigated. This model covers many of the existing models in the literature. It extends the integer order case to the fractional case in the sense of Caputo. A fixed point theorem is used to prove existence of mild solutions.
AMS Subject Classification
26A33, 34K40, 35L90, 35L70, 35L15, 35L07
1 Introduction
In this paper, we investigate the following neutral second-order abstract differential problem

with 0 ≤ α, β, γ ≤ 1. Here, the prime denotes time differentiation and C D κ, κ = α, β, γ denotes fractional time differentiation (in the sense of Caputo). The operator A is the infinitesimal generator of a strongly continuous cosine family C(t), t ≥ 0 of bounded linear operators in the Banach space X and f, g are nonlinear functions from R + × X × X to X, u 0 and u 1 are given initial data in X. The functions p : [C(I; X)]2 → X, q : [C(I; X)]2 → X are given continuous functions (see the example at the end of the paper).
This problem has been studied in case α, β, γ are 0 or 1 (see [1–8]). Well-posedness has been established using different fixed point theorems and the theory of strongly continuous cosine families in Banach spaces. We refer the reader to [7, 9, 10] for a good account on the theory of cosine families.
Fractional non-local conditions are the natural generalization of the integer order non-local conditions as studied by Hernandez [5] and others. They include the discrete case where the solution is prescribed at some finite number of times.
Time delay is a natural phenomena which occurs in many problems (see [11, 12]). It is caused for instance by the finite switching speed of amplifiers in electronic networks or finite speed for signal propagation in biological networks. We can trace problems with delays back to Volterra who introduced past states in population dynamics. It has been also introduced by Boltzmann in viscoelasticity in the form of a convolution. When there is a dependence on all past states we usually call such a delay a distributed delay. There are in fact several types of delays. The importance of delays has been pointed out by many researchers and we are now witnessing a growing interest in such problems. An important class of delayed differential equations (or functional differential equations) is the class of neutral differential equations. In this type of problems the delayed argument occurs in the derivative of the state variable. This is the case, for instance, when a growing population consumes more (or less) food than matured one or when this term appears in the constitutive relationship between the stress and the strain. In fact, neutral differential equations arise naturally in biology, ecology, electronics, economics, epidemiology, control theory and mechanics [11–18]. More precisely, they appear in the study of oscillatory systems, electrical networks containing lossless transmission line (high-speed computers, distributed non-lumped transmission line, lossless transmission line terminated by a tunnel diode and lumped parallel capacitor) [11, 13, 15, 18], vibrating masses attached to an elastic bar [11, 12], automatic control, neuro-mechanical systems and some variational problems (Euler equations) [14, 16, 17]. For the sake of simplicity and since the case where time delay exists in the function "g" has been already studied before (at least for some types of delays) we shall focus on the distributed delay present in the nonlinearity "f ".
We consider the case (g ≢ 0) and prove existence of mild solutions under different conditions on the different data. In particular, this work may be viewed as an extension of the work in [6] to the fractional order case. Indeed, the work in [6] is concerned with the first-order derivatives whereas here we treat the fractional order case where some difficulties arise because of the non-local nature of the fractional derivatives. In addition to that, to the best of the author's knowledge, fractional derivatives are introduced here for such problems for the first time.
The next section of this paper contains some notation and preliminary results needed in our proofs. Section 3 treats the existence of a mild solution in the space of continuously differentiable functions. An example is provided to illustrate our finding.
2 Preliminaries
In this section, we present some notation, assumptions and preliminary results needed in our proofs later.
Definition 1. The integral

is called the Riemann-Liouville fractional integral of h of order α > 0 when the right side exists.
Here, Γ is the usual Gamma function

Definition 2. The fractional derivative of h of order α > 0 in the sense of Caputo is given by

In particular

See [19–22] for more on fractional derivatives and fractional integrals.
We will assume that (H1) A is the infinitesimal generator of a strongly continuous cosine family C(t), t ∈ R, of bounded linear operators in the Banach space X.
The associated sine family S(t), t ∈ R is defined by

It is known (see [7, 8, 10]) that there exist constants M ≥ 1 and ω ≥ 0 such that

For simplicity, we will designate by  and
and  bounds for C(t) and S(t) on I = [0, T], respectively.
bounds for C(t) and S(t) on I = [0, T], respectively.
If we define

then we have
Assume that (H 1) is satisfied . Then
-
(i)
S(t)X ⊂ E, t ∈ R,
-
(ii)
S(t)E ⊂ D(A), t ∈ R,
-
(iii)
 ,
, -
(iv)

Suppose that (H1) holds, v : R → X a continuously differentiable function and  . Then, q(t) ∈ D(A),
. Then, q(t) ∈ D(A),  and
and 
Definition 3. A continuously differentiable function u satisfying the integro-differential equation

is called a mild solution of problem (1).
This definition follows directly from the definition of the cosine family and (1), see [6, 7].
3 Existence of mild solutions
In this section, we prove existence of a mild solution in the space C 1(I; X). Before we proceed with the assumptions on the different data we recall that E is a Banach space when endowed with the norm ||x|| E = ||x|| + sup0≤t≤1||AS(t)x||, x ∈ E (see [23]). It is also well-known that AS(t) : E → X is a bounded linear operator. By B r (x, X) we will denote the closed ball in X centered at x and of radius r.
The assumptions on f, g, p and q are (H2)
-
(i)
f(t,.,.) : X × X → X is continuous for a.e. t ∈ I.
-
(ii)
For every (x, y) ∈ X × X, the function f(.,x, y) : I → X is strongly measurable.
-
(iii)
There exist a nonnegative continuous function K f (t) and a continuous nondecreasing positive function Ω f such that
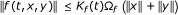
for (t, x, y) ∈ I × X × X.
-
(iv)
For each r > 0, the set f(I × B r (0, X 2)) is relatively compact in X.
(H3)
-
(i)
The function g takes its values in E and g : I × X × X → X is continuous.
-
(ii)
There exist a nonnegative continuous function K g (t), a continuous non-decreasing positive function Ω g and two positive constants C 1, C 2 such that
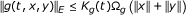
and
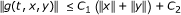
for (t, x, y) ∈ I × X × X.
-
(iii)
The family of functions {t → g(t, u, v); u, v ∈ B r (0, C(I; X))} is equicontinuous on I.
-
(iv)
For each r > 0, the set g(I × B r (0, X 2)) is relatively compact in E.
(H4) u 0+p : [C(I; X)]2 → E (takes its values in E) and q : [C(I; X)]2 → X are completely continuous.
The positive constants N p and N q will denote bounds for ||u 0 + p(u, v)|| E and ||q(u, v)||, respectively. To lighten the statement of our result we denote by

and

We are now ready to state and prove our result.
Theorem 1. Assume that (H1)-(H4) hold. If l > 0 and

then problem (1) admits a mild solution u ∈ C 1([0, T]).
Proof. Note that by our assumptions and for u, v ∈ C([0, T]); the maps

and

are well defined, and map [C([0, T])]2 into C([0, T]). These maps are nothing but the right hand side of (2) and its derivative. We would like to apply the Leray-Schauder alternative [which states that either the set of solutions of (6) (below) is unbounded or we have a fixed point in D (containing zero) a convex subset of X provided that the mappings Φ and Ψ are completely continuous]. To this end, we first prove that the set of solutions (u λ , v λ ) of

is bounded. Then, we prove that this map is completely continuous. Therefore, there remains the alternative which is the existence of a fixed point. We have from (4)

and from (5)

Then

and

where

and

Taking the sup in the relation (7) and max  sup in the relation (8) and adding the resulting expressions we end up with
sup in the relation (8) and adding the resulting expressions we end up with

where Λ(z) is equal to the expression

and

or simply

With

and

provided that

If we designate by φ λ (t) the right hand side of (9), then

Θλ (t) ≤ φ λ (t), t ∈ I and

We infer that

This (with (3)) shows that Θλ(t) and thereafter the set of solutions of (6) is bounded in [C(I; X)]2 :
It remains to show that the maps Φ and Ψ are completely continuous. From our hypotheses it is immediate that

is completely continuous. To apply Ascoli-Arzela theorem we need to check that

is equicontinuous on I. Let us observe that

for t ∈ I and h such that t + h ∈ I. In virtue of (H1) and (H3), for t ∈ I and ε > 0 given, there exists δ > 0 such that

for s ∈ [0, t] and  , when |h| < δ. This together with (H2), (H3) and the fact that S(t) is Lipschitzian imply that
, when |h| < δ. This together with (H2), (H3) and the fact that S(t) is Lipschitzian imply that

for some positive constant N l : The equicontinuity is therefore established.
On the other hand, for t ∈ I, as (s,ξ) → C(t - s)ξ is continuous from  to X and
to X and  is relatively compact,
is relatively compact,

is relatively compact as well in X. As for Φ3 := Φ - Φ1 + Φ2 we decompose it as follows

and select the partition  of [0, t] in such a manner that, for a given ε > 0
of [0, t] in such a manner that, for a given ε > 0

for  , when s, s' ∈ [s
i
, s
i+1] for some i = 1,..., k - 1: This is possible in as much as
, when s, s' ∈ [s
i
, s
i+1] for some i = 1,..., k - 1: This is possible in as much as

is bounded (by (H2)(iii)) and the operator S is uniformly Lipschitz on I. This leads to

where

and co(U(t, s
i
, r)) designates its convex hull. Therefore,  is relatively compact in X. By Ascoli-Arzela Theorem,
is relatively compact in X. By Ascoli-Arzela Theorem,  is relatively compact in C(I; X) and consequently Φ3 is completely continuous. Similarly, we may prove that Ψ is completely continuous.
is relatively compact in C(I; X) and consequently Φ3 is completely continuous. Similarly, we may prove that Ψ is completely continuous.
We conclude that (Φ, Ψ) admits a fixed point in [C([0, T])]2 .
Remark 1. In the same way we may treat the more general case

where 0 ≤ α i , β j , γ k ≤ 1, i = 1,..., n, j = 1,..., m, k = 1,...,r.
Remark 2. If g does not depend on u'(t), that is for g(t, u(t)), we may avoid the condition that g must be an E-valued function. We require instead that g be continuously differentiable and apply Lemma 2 to

to obtain

instead of

in (5).
Example As an example we may consider the following problem

in the space X = L 2([0, π]). This problem can be reformulated in the abstract setting (1). To this end, we define the operator Ay = y" with domain

The operator A has a discrete spectrum with -n
2, n = 1, 2,... as eigenvalues and  , n = 1, 2,... as their corresponding normalized eigenvectors. So we may write
, n = 1, 2,... as their corresponding normalized eigenvectors. So we may write

Since -A is positive and self-adjoint in L 2([0, π]), the operator A is the infinitesimal generator of a strongly continuous cosine family C(t), t ∈ R which has the form

The associated sine family is found to be

One can also consider more general non-local conditions by allowing the Lebesgue measure ds to be of the form dμ(s) and dη(s) (Lebesgue-Stieltjes measures) for non-decreasing functions μ and η (or even more general: μ and η of bounded variation), that is

These (continuous) non-local conditions cover, of course, the discrete cases

which have been extensively studied by several authors in the integer order case.
For u, v ∈ C([0, T]; X) and x ∈ [0, π], defining the operators

allows us to write (10) abstractly as

Under appropriate conditions on F, G, P and Q which make (H2)-(H4) hold for the corresponding f, g, p and q, Theorem 1 ensures the existence of a mild solution to problem (10).
Some special cases of this problem may be found in [24–28]. They model some phenomena with hereditary properties. See also [29–33] for some problems with fractional boundary conditions.
References
Benchohra M, Ntouyas SK: Existence of mild solutions of second order initial value problems for delay integrodifferential inclusions with nonlocal conditions. Math Bohemica 2002,4(127):613-622.
Benchohra M, Ntouyas SK: Existence results for the semiinfinite interval for first and second-order integrodifferential equations in Banach spaces with nonlocal conditions. Acta Univ Palacki Olomuc Fac Rer Nat Math 2002, 41: 13-19.
Benchohra M, Ntouyas SK: Existence results for multivalued semilinear functional differential equations. Extr Math 2003,18(1):1-12.
Byszewski L, Laksmikantham V: Theorems about the existence and uniqueness of a solution of a nonlocal abstract Cauchy problem in a Banach space. Appl Anal 1991,40(1):11-19. 10.1080/00036819008839989
Hernandez ME: Existence results for a second order abstract Cauchy problem with nonlocal conditions. Electron J Differ Equ 2005,2005(73):1-17.
Hernandez EM, Henríquez HR, McKibben MA: Existence of solutions for second order partial neutral functional differential equations. Integr Equ Oper Theory 2008, 62: 191-217. 10.1007/s00020-008-1618-1
Travis CC, Webb GF: Cosine families and abstract nonlinear second order differential equations. Acta Math Acad Sci Hung 1978, 32: 76-96.
Travis CC, Webb GF: An abstract second order semilinear Volterra integrodifferential equation. SIAM J Math Anal 1979,10(2):412-424. 10.1137/0510038
Fattorini HO: Second Order Linear Differential Equations in Banach Spaces. North-Holland Mathematics Studies, North-Holland, Amsterdam 1985., 108:
Travis CC, Webb GF: Compactness, regularity and uniform continuity properties of strongly continuous cosine families. Houston J Math 1977,3(4):555-567.
El'sgol'tz LE: Introduction to the Theory of Differential Equations with Deviating Arguments. Holden-Day, San Francisco; 1966.
Hale JK: Theory of Functional Differential Equations. Springer-Verlag, New York; 1977.
El'sgol'tz LE: Qualitative Methods in Mathematical Analysis. Transaction on Mathematical Monographs, American Mathematical Society, Providence 1964., 12:
Hughes DK: Variational and optimal control problems with delayed arguments. J Optim Theory Appl 1968, 2: 1-14. 10.1007/BF00927159
Nagumo J, Shimura M: Self-oscillation in a transmission line with a tunnel diode. Proc IRE 1961, 49: 1281-1291.
Rubanik VP: Oscillations of Quasilinear Systems with Retardation. Nauk, Moscow; 1969.
Sabbagh LD: Variational problems with lags. J Optim Theory Appl 1969, 3: 34-51. 10.1007/BF00929540
Shimura M: Analysis of some nonlinear phenomena in a transmission line. IEEE Trans Circ Theory 1967, 14: 60-68.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York; 1993.
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York; 1974.
Podlubny I: Fractional Differential Equations. In Mathematics in Sciences and Engineering. Volume 198. Academic Press, San Diego; 1999.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Theory and Applications. Gordon and Breach, Yverdon 1993.
Kisyński J: On cosine operator functions and some parameter group of operators. Stud Math 1972, 49: 93-105.
Chen W, Holm S: Modified Szabo's wave equation models for lossy media obeying frequency power law. J Acoust Soc Am 2003,114(5):2570-2575. 10.1121/1.1621392
Fukunaga M, Shimizu N: Role of prehistories in the initial value problem of fractional viscoelastic equations. Nonlinear Dyn 2004, 38: 207-220. 10.1007/s11071-004-3756-6
Haddar H, Li J-R, Matignon D: Efficient solution of a wave equation with fractional-order dissipative terms. J Comput Appl Math 2010,234(6):2003-2010. 10.1016/j.cam.2009.08.051
Hedrich KS, Filipovski A: Longitudinal creep vibrations of a fractional derivative order rheological rod with variable cross section. Facta Univ Ser Mech Autom Control Robot 2002,3(12):327-349.
Orsingher E, Beghin L: Time-fractional telegraph equations and telegraph processes with Brownian time. Probab. Theory Relat Fields 2004, 128: 141-160. 10.1007/s00440-003-0309-8
Kirane M, Tatar N-e: Absence of local solutions to an elliptic system with time-fractional dynamical boundary conditions. Sib Math J 2007,48(3):477-488. 10.1007/s11202-007-0050-0
Labidi S, Tatar N-e: Blow up for the Euler-Bernoulli beam problem with a fractional boundary condition. Dyn Syst Appl 2008, 17: 109-120.
Labidi S, Tatar N-e: Unboundedness for the Euler-Bernoulli beam equation with fractional boundary dissipation. Appl Math Comp 2005,161(3):697-706. 10.1016/j.amc.2003.12.057
Labidi S, Tatar N-e: Breakdown for a Kirchhoff type beam with a fractional boundary feedback. J Dyn Control Syst 2008,14(1):71-94. 10.1007/s10883-007-9031-7
Mbodje B: Wave energy decay under fractional derivative controls. IMA J Math Control Inf 2006,23(2):237-257.
Acknowledgements
The author is very grateful for the financial support provided by King Fahd University of Petroleum and Minerals through the project No. IN 100007.
Author information
Authors and Affiliations
Corresponding author
Additional information
4 Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tatar, Ne. Mild solutions for a problem involving fractional derivatives in the nonlinearity and in the non-local conditions. Adv Differ Equ 2011, 18 (2011). https://doi.org/10.1186/1687-1847-2011-18
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2011-18
 ,
,