- Research Article
- Open access
- Published:
On the identity of two q-discrete Painlevé equations and their geometrical derivation
Advances in Difference Equations volume 2006, Article number: 036397 (2006)
Abstract
We show that two recently discovered q-discrete Painlevé equations are one and the same system. Moreover we provide a novel derivation of this q-discrete system based on transformations obtained with the help of affine Weyl groups.
References
Grammaticos B, Ramani A: On a novel q -discrete analogue of the Painlevé VI equation. Physics Letters. A 1999,257(5–6):288–292. 10.1016/S0375-9601(99)00296-0
Grammaticos B, Ramani A: Generating discrete Painlevé equations from affine Weyl groups. Regular & Chaotic Dynamics 2005,10(2):145–152. 10.1070/RD2005v010n02ABEH000308
Grammaticos B, Ramani A, Papageorgiou V: Do integrable mappings have the Painlevé property? Physical Review Letters 1991,67(14):1825–1828. 10.1103/PhysRevLett.67.1825
Hietarinta J, Viallet C: Singularity confinement and chaos in discrete systems. Physical Review Letters 1998,81(2):325–328. 10.1103/PhysRevLett.81.325
Jimbo M, Sakai H: A q -analog of the sixth Painlevé equation. Letters in Mathematical Physics 1996,38(2):145–154. 10.1007/BF00398316
Kajiwara K, Noumi M, Yamada Y: Discrete dynamical systems with
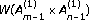 symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276
symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276Masuda T: On the rational solutions of q -Painlevé V equation. Nagoya Mathematical Journal 2003, 169: 119–143.
Okamoto K: Sur les feuilletages associés aux équations du second ordre à points critiques fixes de P. Painlevé. Japanese Journal of Mathematics. New Series 1979,5(1):1–79.
Quispel GRW, Roberts JAG, Thompson CJ: Integrable mappings and soliton equations. II. Physica D. Nonlinear Phenomena 1989,34(1–2):183–192. 10.1016/0167-2789(89)90233-9
Ramani A, Ohta Y, Satsuma J, Grammaticos B: Self-duality and Schlesinger chains for the asymmetric d - P II and q - P III equations. Communications in Mathematical Physics 1998,192(1):67–76. 10.1007/s002200050291
Ramani A, Willox R, Grammaticos B, Carstea AS, Satsuma J: Limits and degeneracies of discrete Painlevé equations: a sequel. Physica A: Statistical and Theoretical Physics 2005,347(1–4):1–16.
Sakai H: Rational surfaces associated with affine root systems and geometry of the Painlevé equations. Communications in Mathematical Physics 2001,220(1):165–229. 10.1007/s002200100446
Takenawa T: Weyl group symmetry of type
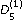 in the q -Painlevé V equation. Funkcialaj Ekvacioj. Serio Internacia 2003,46(1):173–186. 10.1619/fesi.46.173
in the q -Painlevé V equation. Funkcialaj Ekvacioj. Serio Internacia 2003,46(1):173–186. 10.1619/fesi.46.173
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Grammaticos, B., Ramani, A. & Takenawa, T. On the identity of two q-discrete Painlevé equations and their geometrical derivation. Adv Differ Equ 2006, 036397 (2006). https://doi.org/10.1155/ADE/2006/36397
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ADE/2006/36397
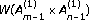 symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276
symmetry. Letters in Mathematical Physics 2002,60(3):211–219. 10.1023/A:1016298925276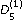 in the q -Painlevé V equation. Funkcialaj Ekvacioj. Serio Internacia 2003,46(1):173–186. 10.1619/fesi.46.173
in the q -Painlevé V equation. Funkcialaj Ekvacioj. Serio Internacia 2003,46(1):173–186. 10.1619/fesi.46.173