- Research Article
- Open access
- Published:
Solutions to a Three-Point Boundary Value Problem
Advances in Difference Equations volume 2011, Article number: 894135 (2011)
Abstract
By using the fixed-point index theory and Leggett-Williams fixed-point theorem, we study the existence of multiple solutions to the three-point boundary value problem  ,
,  ;
;  ;
;  , where
, where  ,
,  are constants,
are constants,  is a parameter, and
is a parameter, and  ,
,  are given functions. New existence theorems are obtained, which extend and complement some existing results. Examples are also given to illustrate our results.
are given functions. New existence theorems are obtained, which extend and complement some existing results. Examples are also given to illustrate our results.
1. Introduction
It is known that when differential equations are required to satisfy boundary conditions at more than one value of the independent variable, the resulting problem is called a multipoint boundary value problem, and a typical distinction between initial value problems and multipoint boundary value problems is that in the former case one is able to obtain the solutions depend only on the initial values, while in the latter case, the boundary conditions at the starting point do not determine a unique solution to start with, and some random choices among the solutions that satisfy these starting boundary conditions are normally not to satisfy the boundary conditions at the other specified point(s). As it is noticed elsewhere (see, e.g., Agarwal [1], Bisplinghoff and Ashley [2], and Henderson [3]), multi point boundary value problem has deep physical and engineering background as well as realistic mathematical model. For the development of the research of multi point boundary value problems for differential equations in last decade, we refer the readers to, for example, [1, 4–9] and references therein.
In this paper, we study the existence of multiple solutions to the following three-point boundary value problem for a class of third-order differential equations with inhomogeneous three-point boundary values,

where  ,
,  ,
,  , and
, and  ,
,  are given functions. To the authors' knowledge, few results on third-order differential equations with inhomogeneous three-point boundary values can be found in the literature. Our purpose is to establish new existence theorems for (1.1) which extend and complement some existing results.
are given functions. To the authors' knowledge, few results on third-order differential equations with inhomogeneous three-point boundary values can be found in the literature. Our purpose is to establish new existence theorems for (1.1) which extend and complement some existing results.
Let  be an Banach space, and let
be an Banach space, and let  be a cone in
be a cone in  . A mapping
. A mapping  is said to be a nonnegative continuous concave functional on
is said to be a nonnegative continuous concave functional on  if
if  is continuous and
is continuous and

Assume that
-
(H)
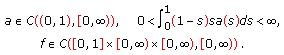 (1.3)
(1.3)
Define

This paper is organized in the following way. In Section 2, we present some lemmas, which will be used in Section 3. The main results and proofs are given in Section 3. Finally, in Section 4, we give some examples to illustrate our results.
2. Lemmas
Let  be a Banach Space with norm
be a Banach Space with norm

where

It is not hard to see Lemmas 2.1 and 2.2.
Lemma 2.1.
Let  be the unique solution of (1.1). Then
be the unique solution of (1.1). Then

where

Lemma 2.2.
One has the following.
-
(i)
 .
. -
(ii)
 .
. -
(iii)
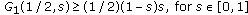 .
.
Lemma 2.3.
Let  be the unique solution of (1.1). Then
be the unique solution of (1.1). Then  is nonnegative and satisfies
is nonnegative and satisfies  .
.
Proof.
Let  be the unique solution of (1.1). Then it is obvious that
be the unique solution of (1.1). Then it is obvious that  is nonnegative. By Lemmas 2.1 and 2.2, we have the following.
is nonnegative. By Lemmas 2.1 and 2.2, we have the following.
-
(i)
For
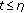 ,
,  (2.5)
(2.5)
that is,  .
.
-
(ii)
For
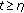 ,
,  (2.6)
(2.6)
On the other hand, for  , we have
, we have

Since  ,
,

So,  . Therefore,
. Therefore,  , which means
, which means

The proof is completed.
Lemma 2.4.
Let  be the unique solution of (1.1). Then
be the unique solution of (1.1). Then

Proof.
From (2.3), it follows that

Hence,

By Lemmas 2.2 and 2.3, we get, for any  ,
,

Thus,

Define a cone by

Set

Define an operator  by
by

Lemma 2.1 implies that (1.1) has a solution  if and only if
if and only if  is a fixed point of
is a fixed point of  .
.
From Lemmas 2.1 and 2.2 and the Ascoli-Arzela theorem, the following follow.
Lemma 2.5.
The operator defined in (2.17) is completely continuous and satisfies  .
.
Theorem 2.6 (see [10]).
Let  be a real Banach Space, let
be a real Banach Space, let  be a cone, and
be a cone, and  . Let operator
. Let operator  be completely continuous and satisfy
be completely continuous and satisfy  ,
,  . Then
. Then
(i)if  , for all
, for all  , then
, then  ,
,
(ii)if  , for all
, for all  , then
, then  .
.
Theorem 2.7 (see [8]).
Let  be a completely continuous operator and
be a completely continuous operator and  a nonnegative continuous concave functional on
a nonnegative continuous concave functional on  such that
such that  for all
for all  . Suppose that there exist
. Suppose that there exist  such that
such that
-
(a)
 and
and 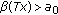 for
for  ,
, -
(b)
 for
for 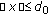 ,
, -
(c)
 for
for 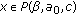 with
with  .
.
Then,  has at least three fixed points
has at least three fixed points  in
in  satisfying
satisfying

3. Main Results
In this section, we give new existence theorem about two positive solutions or three positive solutions for (1.1).
Write

Theorem 3.1.
Assume that
 ;
;
there exists a constant  such that
such that  , for
, for  ,
,  and
and  .
.
Then, the problem (1.1) has at least two positive solutions  and
and  such that
such that

for  small enough.
small enough.
Proof.
Since

there is  such that
such that

Let

Then, for any  , it follows from Lemmas 2.2 and 2.3 and (3.4) that
, it follows from Lemmas 2.2 and 2.3 and (3.4) that

Hence,

So

By Theorem 2.6, we have

On the other hand, since

there exist  ,
,  such that
such that

Let  . Then, by a argument similar to that above, we obtain
. Then, by a argument similar to that above, we obtain

By Theorem 2.6,

Finally, let  , and let
, and let  satisfy
satisfy  for any
for any  . Then,
. Then,  implies
implies

which means that  . Thus,
. Thus,  , for all
, for all  .
.
Using Theorem 2.6, we get

From (3.9)–(3.15) and  , it follows that
, it follows that

Therefore,  has fixed point
has fixed point  and fixed point
and fixed point  . Clearly,
. Clearly,  ,
,  are both positive solutions of the problem (1.1) and
are both positive solutions of the problem (1.1) and

The proof of Theorem 3.1 is completed.
Theorem 3.2.
Assume that
 ;
;
there exists a constant  such that
such that  , for
, for  and
and  .
.
Then, the problem (1.1) has at least two positive solutions  and
and  such that
such that

for  small enough.
small enough.
Proof.
By

we see that there exists  such that
such that

Put

and let  satisfy
satisfy

Then Lemmas 2.2 and 2.3 and (3.20) implies that for any  ,
,

So  . Hence,
. Hence,  ,
,  .
.
Applying Theorem 2.6, we have

Next, by

we know that there exists  such that
such that

Case 1.
 is unbounded.
is unbounded.
Define a function  by
by

Clearly,  is nondecreasing and
is nondecreasing and  , and
, and

Taking  , it follows from (3.26)–(3.28) that
, it follows from (3.26)–(3.28) that

By Lemmas 2.2 and 2.3 and (3.28), we have

So  , and then
, and then  .
.
Case 2.
 is bounded.
is bounded.
In this case, there exists an  such that
such that

Choosing  , we see by Lemmas 2.2 and 2.3 and (3.31) that
, we see by Lemmas 2.2 and 2.3 and (3.31) that

which implies  , and then
, and then  .
.
Therefore, in both cases, taking

we get

By Theorem 2.6, we have

Finally, put  . Then
. Then  implies that
implies that

that is,  , and then
, and then  , for all
, for all  . By virtue of Theorem 2.6, we have
. By virtue of Theorem 2.6, we have

From (3.24), (3.35), (3.37), and  , it follows that
, it follows that

Hence,  has fixed point
has fixed point  and fixed point
and fixed point  . Obviously,
. Obviously,  ,
,  are both positive solutions of the problem (1.1) and
are both positive solutions of the problem (1.1) and

The proof of Theorem 3.2 is completed.
Theorem 3.3.
Let there exist  ,
,  ,
,  , and
, and  with
with

such that



Then problem (1.1) has at least three positive solutions  ,
,  ,
,  satisfying
satisfying

for  .
.
Proof.
Let

Then,  is a nonnegative continuous concave functional on
is a nonnegative continuous concave functional on  and
and  for each
for each  . Let
. Let  be in
be in  . Equation (3.43) implies that
. Equation (3.43) implies that

Hence,  . This means that
. This means that  .
.
Take

Then,

By (3.42), we have, for any  ,
,

Therefore,  in Theorem 2.7 holds.
in Theorem 2.7 holds.
By (3.41), we see that for any 

So,  . This means that
. This means that  of Theorem 2.7 holds.
of Theorem 2.7 holds.
Moreover, for any  with
with  , we have
, we have

which implies

So,  in Theorem 2.7 holds. Thus, by Theorem 2.7, we know that the operator
in Theorem 2.7 holds. Thus, by Theorem 2.7, we know that the operator  has at least three positive fixed points
has at least three positive fixed points  satisfying
satisfying

4. Examples
In this section, we give three examples to illustrate our results.
Example 4.1.
Consider the problem

where  ,
,  . Set
. Set

Then,

So, the condition  is satisfied. Observe
is satisfied. Observe

Taking

we have

Thus, condition  is satisfied.
is satisfied.
Therefore, by Theorem 3.1, the problem (4.1) has at least two positive solutions  and
and  such that
such that

for

Example 4.2.
Consider the problem

where  ,
,  . Set
. Set

Then,

that is, the condition  is satisfied. Moreover,
is satisfied. Moreover,

Taking

we get

Thus, condition  is satisfied.
is satisfied.
Consequently, by Theorem 3.2, we see that for

the problem (4.9) has at least two positive solutions  and
and  such that
such that

Example 4.3.
For the problem (1.1), take  ,
,  , and
, and  . Then,
. Then,

Let

Then,

which implies

That is, the conditions of Theorem 3.3 are satisfied. Consequently, the problem (1.1) has at least three positive solutions  for
for

satisfying

References
Agarwal RP: Focal Boundary Value Problems for Differential and Difference Equations, Mathematics and Its Applications. Volume 436. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1998:x+289.
Bisplinghoff RL, Ashley H: Principles of Aeroelasticity. Dover Publications, Mineola, NY, USA; 2002.
Henderson J (Ed): Boundary Value Problems for Functional-Differential Equations. World Scientific, River Edge, NJ, USA; 1995:x+306.
Anderson DR: Green's function for a third-order generalized right focal problem. Journal of Mathematical Analysis and Applications 2003,288(1):1-14. 10.1016/S0022-247X(03)00132-X
Avery RI, Peterson AC: Three positive fixed points of nonlinear operators on ordered Banach spaces. Computers & Mathematics with Applications 2001,42(3–5):313-322.
Boucherif A, Al-Malki N: Nonlinear three-point third-order boundary value problems. Applied Mathematics and Computation 2007,190(2):1168-1177. 10.1016/j.amc.2007.02.039
Karakostas GL, Mavridis KG, Tsamatos PC: Triple solutions for a nonlocal functional boundary value problem by Leggett-Williams theorem. Applicable Analysis 2004,83(9):957-970. 10.1080/00036810410001724571
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana University Mathematics Journal 1979,28(4):673-688. 10.1512/iumj.1979.28.28046
Sun Y: Positive solutions for third-order three-point nonhomogeneous boundary value problems. Applied Mathematics Letters 2009,22(1):45-51. 10.1016/j.aml.2008.02.002
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgments
This paper was supported partially by the NSF of China (10771202) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (2007035805).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liang, J., Lv, ZW. Solutions to a Three-Point Boundary Value Problem. Adv Differ Equ 2011, 894135 (2011). https://doi.org/10.1155/2011/894135
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/894135
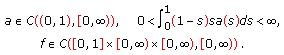
 .
. .
.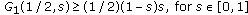 .
.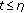 ,
, 
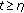 ,
, 
 and
and 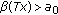 for
for  ,
, for
for 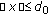 ,
, for
for 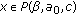 with
with  .
.