- Research Article
- Open access
- Published:
Solvability of Nonautonomous Fractional Integrodifferential Equations with Infinite Delay
Advances in Difference Equations volume 2011, Article number: 806729 (2011)
Abstract
We study the existence and uniqueness of mild solution of a class of nonlinear nonautonomous fractional integrodifferential equations with infinite delay in a Banach space  . The existence of mild solution is obtained by using the theory of the measure of noncompactness and Sadovskii's fixed point theorem. An application of the abstract results is also given.
. The existence of mild solution is obtained by using the theory of the measure of noncompactness and Sadovskii's fixed point theorem. An application of the abstract results is also given.
1. Introduction
The Cauchy problem for various delay equations in Banach spaces has been receiving more and more attention during the past decades (cf., e.g., [1–15]). This paper is concerned with existence results for nonautonomous fractional integrodifferential equations with infinite delay in a Banach space 

where  ,
,  ,
,  is a family of linear operators in
is a family of linear operators in  with
with  and
and

 ,
,  defined by
defined by  for
for  ,
,  belongs to the phase space
belongs to the phase space  , and
, and  . The fractional derivative is understood here in the Riemann-Liouville sense.
. The fractional derivative is understood here in the Riemann-Liouville sense.
In recent years, the fractional differential equations have been proved to be good tools in the investigation of many phenomena in engineering, physics, economy, chemistry, aerodynamics, electrodynamics of complex medium and they have been studied by many researchers (cf., e.g., [13, 14, 16, 17] and references therein). Moreover, many phenomena cannot be described through classical differential equations but the integral and integrodifferential equations in abstract spaces in fields like electronic, fluid dynamics, biological models, and chemical kinetics. So many significant works on this topic have been appeared (cf., e.g., [10, 15, 18–25] and references therein).
In this paper, we study the existence of mild solution of (1.1) and obtain the existence theorem based on the measures of noncompactness without the assumptions that the nonlinearity  satisfies a Lipschitz type condition and the semigroup
satisfies a Lipschitz type condition and the semigroup  generated by
generated by  is compact (see Theorem 3.1). An example is given to show an application of the abstract results.
is compact (see Theorem 3.1). An example is given to show an application of the abstract results.
2. Preliminaries
Throughout this paper, we set  , a compact interval in
, a compact interval in  . We denote by
. We denote by  a Banach space,
a Banach space,  the Banach space of all linear and bounded operators on
the Banach space of all linear and bounded operators on  , and
, and  the space of all
the space of all  -valued continuous functions on
-valued continuous functions on  . We set
. We set

Next, we recall the definition of the Riemann-Liouville integral.
Definition 2.1 (see [26]).
The fractional (arbitrary) order integral of the function  of order
of order  is defined by
is defined by

where  is the Gamma function. Moreover,
is the Gamma function. Moreover,  , for all
, for all  .
.
Remark 2.2.
-
(1)
 (see [26]),
(see [26]), -
(2)
obviously, for
 , it follows from Definition 2.1 that
, it follows from Definition 2.1 that 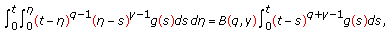 (2.3)
(2.3)
where  is a beta function.
is a beta function.
See the following definition about phase space according to Hale and Kato [27].
Definition 2.3.
A linear space  consisting of functions from
consisting of functions from  into
into  , with seminorm
, with seminorm  , is called an admissible phase space if
, is called an admissible phase space if  has the following properties.
has the following properties.
-
(1)
If
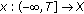 is continuous on
is continuous on 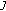 and
and 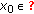 , then
, then 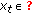 and
and  is continuous in
is continuous in  , and
, and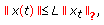 (2.4)
(2.4)where
 is a constant.
is a constant. -
(2)
There exist a continuous function
 and a locally bounded function
and a locally bounded function 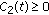 in
in 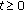 , such that
, such that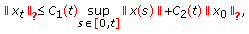 (2.5)
(2.5)for
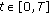 and
and  as in (1).
as in (1). -
(3)
The space
 is complete.
is complete.
Remark 2.4.
Equation (2.4) in (1) is equivalent to  , for all
, for all  .
.
Next, we consider the properties of Kuratowski's measure of noncompactness.
Definition 2.5.
Let  be a bounded subset of a seminormed linear space
be a bounded subset of a seminormed linear space  . The Kuratowski's measure of noncompactness(for brevity,
. The Kuratowski's measure of noncompactness(for brevity,  -measure) of
-measure) of  is defined as
is defined as

From the definition we can get some properties of  -measure immediately, see [28].
-measure immediately, see [28].
Lemma 2.6 (see [28]).
Let  and
and  be bounded subsets of
be bounded subsets of  , then
, then
-
(1)
 , if
, if  ;
; -
(2)
 , where
, where 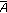 denotes the closure of
denotes the closure of  ;
; -
(3)
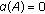 if and only if
if and only if  is precompact;
is precompact; -
(4)
 ,
, ;
; -
(5)
 ;
; -
(6)
 , where
, where  ;
; -
(7)
 , for any
, for any 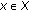 .
.
For  , we define
, we define

where  .
.
The following lemma will be needed.
Lemma 2.7.
If  is a bounded, equicontinuous set, then
is a bounded, equicontinuous set, then
(i) ,
,
(ii) , for
, for  .
.
For a proof refer to [28].
Lemma 2.8 (see [29]).
If  and there exists an
and there exists an  such that
such that  , a.e.
, a.e.  , then
, then  is integrable and
is integrable and

We need to use the following Sadovskii's fixed point theorem here, see [30].
Definition 2.9.
Let  be an operator in Banach space
be an operator in Banach space  . If
. If  is continuous and takes bounded sets into bounded sets, and
is continuous and takes bounded sets into bounded sets, and  for every bounded set
for every bounded set  of
of  with
with  , then
, then  is said to be a condensing operator on
is said to be a condensing operator on  .
.
Lemma 2.10 (Sadovskii's fixed point theorem [30]).
Let  be a condensing operator on Banach space
be a condensing operator on Banach space  . If
. If  for a convex, closed, and bounded set
for a convex, closed, and bounded set  of
of  , then
, then  has a fixed point in
has a fixed point in  .
.
In this paper, we denote that  is a positive constant, and assume that a family of closed linear operators
is a positive constant, and assume that a family of closed linear operators  satisfying the following.
satisfying the following.
(A1)The domain  of
of  is dense in the Banach space
is dense in the Banach space  and independent of
and independent of  .
.
(A2)The operator  exists in
exists in  for any
for any  with Re
with Re  and
and

(A3)There exist constants  and
and  such that
such that

Under condition (A2), each operator  ,
,  , generates an analytic semigroup
, generates an analytic semigroup  ,
,  , and there exists a constant
, and there exists a constant  such that
such that

where  ,
,  ,
,  (see [31]).
(see [31]).
Let  be set defined by
be set defined by

According to [16], a mild solution of (1.1) can be defined as follows.
Definition 2.11.
A function  satisfying the equation
satisfying the equation

is called a mild solution of (1.1), where

and  is a probability density function defined on
is a probability density function defined on  such that its Laplace transform is given by
such that its Laplace transform is given by

where

To our purpose the following conclusions will be needed. For the proofs refer to [16].
Lemma 2.12 (see [16]).
The operator-valued functions  and
and  are continuous in uniform topology in the variables
are continuous in uniform topology in the variables  ,
,  , where
, where  ,
,  , for any
, for any  . Clearly,
. Clearly,

Moreover, we have

3. Main Results
We need the hypotheses as follows:
(H1) satisfies
satisfies  is measurable for all
is measurable for all  and
and  is continuous for a.e.
is continuous for a.e.  , and there exist a positive function
, and there exist a positive function  and a continuous nondecreasing function
and a continuous nondecreasing function  , such that
, such that

and set  ,
,
(H2)for any bounded sets  ,
,  , and
, and  ,
,

where  ,
, and
and  ,
,
(H3)there exists  , with
, with  such that
such that

where  ,
,  and
and  .
.
Theorem 3.1.
Suppose that (H1)–(H3) are satisfied, and if  , then for (1.1) there exists a mild solution on
, then for (1.1) there exists a mild solution on  .
.
Proof.
Consider the operator  defined by
defined by

It is easy to see that  is well-defined.
is well-defined.
Let  be the function defined by
be the function defined by

Let  ,
,  .
.
It is easy to see that  satisfies
satisfies  and
and

if and only if  satisfies
satisfies

and  ,
,  .
.
Let  . For any
. For any  ,
,

Thus  is a Banach space.
is a Banach space.
We define the operator  by
by  ,
,  and
and

Obviously, the operator  has a fixed point if and only if
has a fixed point if and only if  has a fixed point. So it turns out to prove that
has a fixed point. So it turns out to prove that  has a fixed point.
has a fixed point.
Let  be a sequence such that
be a sequence such that  in
in  as
as  . Since
. Since  satisfies (H1), for almost every
satisfies (H1), for almost every  , we get
, we get

For  , we can prove that
, we can prove that  is continuous. In fact,
is continuous. In fact,

Let  , and noting (2.4), (2.5), we have
, and noting (2.4), (2.5), we have

Moreover,

Noting that  in
in  , we can see that there exists
, we can see that there exists  such that
such that  or
or  sufficiently large. Therefore, we have
sufficiently large. Therefore, we have

where

In view of (2.17) and the Lebesgue Dominated Convergence Theorem ensure that

Similarly,by (2.17) and (2.18), we have

Therefore, we deduce that

This means that  is continuous.
is continuous.
We show that  maps bounded sets of
maps bounded sets of  into bounded sets in
into bounded sets in  . For any
. For any  , we set
, we set  . Now, for
. Now, for  , by (3.12), (3.13), and (H1), we can see
, by (3.12), (3.13), and (H1), we can see

where  .
.
Then for any  , by (2.17), (2.18), (3.19), and Remark 2.2, we have
, by (2.17), (2.18), (3.19), and Remark 2.2, we have

where  .
.
Noting that the Hölder inequality, we have

Thus

This means  .
.
Next, we show that there exists  such that
such that  . Suppose contrary that for every
. Suppose contrary that for every  there exist
there exist  and
and  such that
such that  . However, on the other hand, similar to the deduction of (3.20) and noting
. However, on the other hand, similar to the deduction of (3.20) and noting

we have

where  .
.
Dividing both sides of (3.24) by  , and taking
, and taking  , we have
, we have

This contradicts (3.3). Hence for some positive number  ,
,  .
.
Let  and
and  , then
, then

where

It follows from Lemma 2.12, (H1) and (3.23) that  ,
,  , as
, as  .
.
For  , from (2.17), (3.23), and (H1), we have
, from (2.17), (3.23), and (H1), we have

Similarly, by (2.17), (2.18), (H1), and Remark 2.2, we have

So, the set  is equicontinuous.
is equicontinuous.
For every bounded set  and any
and any  , we can take a sequence
, we can take a sequence  such that
such that  (see [32]), thus from Lemmas 2.6–2.8, and 2.12 and (H2), we have
(see [32]), thus from Lemmas 2.6–2.8, and 2.12 and (H2), we have

since  is arbitrary, we can obtain
is arbitrary, we can obtain

In view of the Sadovskii's fixed point theorem, we conclude that  has at least one fixed point
has at least one fixed point  in
in  . Let
. Let  ,
,  , then
, then  is a fixed point of the operator
is a fixed point of the operator  which is a mild solution of (1.1).
which is a mild solution of (1.1).
Now we assume that
(H1') there exists a positive function  , such that
, such that

(H2') there exists a constant  , with
, with  , such that the function
, such that the function  defined by
defined by

Theorem 3.2.
Assume that (H1') and (H2') are satisfied, then (1.1) has a unique mild solution.
Proof.
Let  be defined as in Theorem 3.1. For any
be defined as in Theorem 3.1. For any  ,
,  , we have
, we have

Thus, from (2.17), (2.18), Definition 2.1 and Remark 2.2, we have

So, we get

and the result follows from the contraction mapping principle.
Example 3.3.
We consider the following model:

where  ,
,  ,
,  ,
,  is a continuous function and is uniformly Hölder continuous in
is a continuous function and is uniformly Hölder continuous in  , that is, there exist
, that is, there exist  and
and  such that
such that

 ,
,  are continuous functions, and
are continuous functions, and  .
.
Set  and define
and define  by
by

Then  generates an analytic semigroup
generates an analytic semigroup  satisfying assumptions (A1)–(A3) (see [33]).
satisfying assumptions (A1)–(A3) (see [33]).
Let the phase space  be
be  , the space of bounded uniformly continuous functions endowed with the following norm:
, the space of bounded uniformly continuous functions endowed with the following norm:

then we can see that  in (2.5).
in (2.5).
For  ,
,  and
and  , we set
, we set

where

now  .
.
Then the above equation (3.37) can be written in the abstract form as (1.1).
Moreover,

where  ,
,  satisfy (H1).
satisfy (H1).
For any  ,
,  ,
,

Therefore, for any bounded sets  ,
,  , we have
, we have

Moreover,

Similarly, we obtain

Suppose further that
-
(1)
there exists
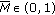 such that
such that  ,
, -
(2)
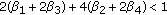 ,
,
then (3.37) has a mild solution by Theorem 3.1.
References
Fan Z: Existence and continuous dependence results for nonlinear differential inclusions with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2379-2392. 10.1016/j.na.2007.08.011
Favini A, Vlasenko L: Degenerate non-stationary differential equations with delay in Banach spaces. Journal of Differential Equations 2003,192(1):93-110. 10.1016/S0022-0396(03)00090-1
Guo Faming, Tang B, Huang F: Robustness with respect to small delays for exponential stability of abstract differential equations in Banach spaces. The ANZIAM Journal 2006,47(4):555-568. 10.1017/S1446181100010130
Liu JH: Periodic solutions of infinite delay evolution equations. Journal of Mathematical Analysis and Applications 2000,247(2):627-644. 10.1006/jmaa.2000.6896
Liu J, Naito T, Van Minh N: Bounded and periodic solutions of infinite delay evolution equations. Journal of Mathematical Analysis and Applications 2003,286(2):705-712. 10.1016/S0022-247X(03)00512-2
Liang J, Xiao TJ: Functional-differential equations with infinite delay in Fréchet space. Sichuan Daxue Xuebao 1989,26(4):382-390.
Liang J, Xiao TJ: Functional-differential equations with infinite delay in Banach spaces. International Journal of Mathematics and Mathematical Sciences 1991,14(3):497-508. 10.1155/S0161171291000686
Liang J, Xiao TJ: Solutions to abstract functional-differential equations with infinite delay. Acta Mathematica Sinica 1991,34(5):631-644.
Liang J, Xiao T-J: The Cauchy problem for nonlinear abstract functional differential equations with infinite delay. Computers & Mathematics with Applications 2000,40(6-7):693-703. 10.1016/S0898-1221(00)00188-7
Liang J, Xiao T-J, van Casteren J: A note on semilinear abstract functional differential and integrodifferential equations with infinite delay. Applied Mathematics Letters 2004,17(4):473-477. 10.1016/S0893-9659(04)90092-4
Liang J, Xiao T-J: Solvability of the Cauchy problem for infinite delay equations. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):271-297. 10.1016/j.na.2004.05.005
Liang J, Xiao T-J: Solutions to nonautonomous abstract functional equations with infinite delay. Taiwanese Journal of Mathematics 2006,10(1):163-172.
Mophou GM, N'Guérékata GM: A note on a semilinear fractional differential equation of neutral type with infinite delay. Advances in Difference Equations 2010, 2010:-8.
Mophou GM, N'Guérékata GM: Existence of mild solutions of some semilinear neutral fractional functional evolution equations with infinite delay. Applied Mathematics and Computation 2010,216(1):61-69. 10.1016/j.amc.2009.12.062
Xiao T-J, Liang J: Blow-up and global existence of solutions to integral equations with infinite delay in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):e1442-e1447. 10.1016/j.na.2009.01.204
El-Borai MM: The fundamental solutions for fractional evolution equations of parabolic type. Journal of Applied Mathematics and Stochastic Analysis 2004, (3):197-211.
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
Chen J-H, Xiao T-J, Liang J: Uniform exponential stability of solutions to abstract Volterra equations. Journal of Evolution Equations 2009,9(4):661-674. 10.1007/s00028-009-0028-4
Liang J, Xiao T-J: Semilinear integrodifferential equations with nonlocal initial conditions. Computers & Mathematics with Applications 2004,47(6-7):863-875. 10.1016/S0898-1221(04)90071-5
Liang J, Liu JH, Xiao T-J: Nonlocal problems for integrodifferential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(6):815-824.
Naito T, Van Minh N, Liu JH: On the bounded solutions of Volterra equations. Applicable Analysis 2004,83(5):433-446. 10.1080/00036810310001632781
Ngoc PHA, Murakami S, Naito T, Shin JS, Nagabuchi Y: On positive linear Volterra-Stieltjes differential systems. Integral Equations and Operator Theory 2009,64(3):325-335. 10.1007/s00020-009-1692-z
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: Approximations of Laplace transforms and integrated semigroups. Journal of Functional Analysis 2000,172(1):202-220. 10.1006/jfan.1999.3545
Xiao T-J, Liang J, van Casteren J: Time dependent Desch-Schappacher type perturbations of Volterra integral equations. Integral Equations and Operator Theory 2002,44(4):494-506. 10.1007/BF01193674
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon, Switzerland; 1993:xxxvi+976.
Hale JK, Kato J: Phase space for retarded equations with infinite delay. Funkcialaj Ekvacioj 1978,21(1):11-41.
Banaś J, Goebel K: Measures of Noncompactness in Banach Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 60. Marcel Dekker, New York, NY, USA; 1980:vi+97.
Heinz H-P: On the behaviour of measures of noncompactness with respect to differentiation and integration of vector-valued functions. Nonlinear Analysis: Theory, Methods & Applications 1983,7(12):1351-1371. 10.1016/0362-546X(83)90006-8
Sadovskii B: On a fixed point principle. Functional Analysis and Its Applications 1967,1(2):151-153.
Hille E, Phillips RS: Functional Analysis and Semi-Groups, American Mathematical Society Colloquium Publications. Volume 31. American Mathematical Society, Providence, RI, USA; 1957:xii+808.
Bothe D: Multivalued perturbations of
 -accretive differential inclusions. Israel Journal of Mathematics 1998, 108: 109-138. 10.1007/BF02783044
-accretive differential inclusions. Israel Journal of Mathematics 1998, 108: 109-138. 10.1007/BF02783044Friedman A: Partial Differential Equations. Holt, Rinehat and Winston, New York, NY, USA; 1969:vi+262.
Acknowledgments
The author is grateful to the referees for their valuable suggestions. This work is supported by the NSF of Yunnan Province (no. 2009ZC054M).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, F. Solvability of Nonautonomous Fractional Integrodifferential Equations with Infinite Delay. Adv Differ Equ 2011, 806729 (2011). https://doi.org/10.1155/2011/806729
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/806729
 (see [
(see [ , it follows from Definition 2.1 that
, it follows from Definition 2.1 that 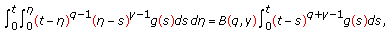
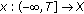 is continuous on
is continuous on 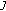 and
and 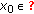 , then
, then 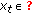 and
and  is continuous in
is continuous in  , and
, and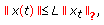
 is a constant.
is a constant. and a locally bounded function
and a locally bounded function 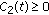 in
in 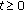 , such that
, such that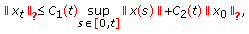
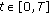 and
and  as in (1).
as in (1). is complete.
is complete. , if
, if  ;
; , where
, where 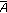 denotes the closure of
denotes the closure of  ;
;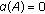 if and only if
if and only if  is precompact;
is precompact; ,
, ;
; ;
; , where
, where  ;
; , for any
, for any 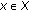 .
.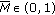 such that
such that  ,
,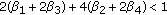 ,
, -accretive differential inclusions. Israel Journal of Mathematics 1998, 108: 109-138. 10.1007/BF02783044
-accretive differential inclusions. Israel Journal of Mathematics 1998, 108: 109-138. 10.1007/BF02783044