- Research Article
- Open access
- Published:
New Existence Results and Comparison Principles for Impulsive Integral Boundary Value Problem with Lower and Upper Solutions in Reversed Order
Advances in Difference Equations volume 2011, Article number: 783726 (2011)
Abstract
This paper investigates the existence of the extremal solutions to the integral boundary value problem for first-order impulsive functional integrodifferential equations with deviating arguments under the assumption of existing upper and lower solutions in the reversed order. The sufficient conditions for the existence of solutions were obtained by establishing several new comparison principles and using the monotone iterative technique. At last, a concrete example is presented and solved to illustrate the obtained results.
1. Introduction
Impulsive differential equations arise naturally from a wide variety of applications, such as control theory, physics, chemistry, population dynamics, biotechnology, industrial robotic, and optimal control ([1–4]). Therefore, it is very important to develop a general theory for differential equations with impulses including some basic aspects of this theory.
In this paper, we consider the following integral boundary value problem for first-order impulsive functional integrodifferential equations with deviating arguments:

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , where
, where  and
and  denote the right and the left limits of
denote the right and the left limits of  at
at  , respectively, and
, respectively, and

here  ,
,  ,
,  ,
,  ,
,  ,
,  . Let
. Let  :
:  is continuous at
is continuous at  , left continuous at
, left continuous at  and
and  exists,
exists,  and
and  is continuously differentiable at
is continuously differentiable at  ,
,  and
and  exist,
exist,  . Evidently,
. Evidently,  and
and  are Banach spaces with respective norms
are Banach spaces with respective norms

In recent years, attention has been given to integral type of boundary conditions. The interest in the study of integral boundary conditions lies in the fact that it has various applications in applied fields such as blood flow problems, chemical engineering, thermoelasticity, underground water flow, and population dynamics. For a detailed description of the integral boundary conditions, we refer the reader to some recent papers ([5–12]) and the references therein.
The method of upper and lower solutions coupled with its associated monotone iteration scheme is an interesting and powerful mechanism that offers the theoretical as well constructive existence results for nonlinear problem in a closed set, generated by the lower and upper solutions (see [9–26]). In the above-mentioned papers, main results are formulated and proved under the assumption of existing upper and lower solutions in the usual order.
However in many cases, the lower and upper solutions occur in the reversed order. This is a fundamentally different situation. In 2009, Wang et al. [27] successfully investigated boundary value problem for functional differential equations without impulses under the assumption of existing upper and lower solutions in the reversed order. In our recent work [28], the monotone iterative technique, combining with the upper and lower solutions in the reversed order, has been successfully applied to obtain the existence of the extremal solutions for a class of nonlinear first-order impulsive functional differential equations. About other existence results for the nonordered case, see ([29–33]).
Motivated by the above-mentioned works, in this paper, we study the integral boundary value problem (1.1). As far as I am concerned, no paper has considered first-order impulsive functional integrodifferential equations with integral boundary conditions and deviating arguments (i.e., problem (1.1)) under the assumption of existing upper and lower solutions in the reverse order. This paper fills this gap in the literature.
The rest of the paper is organized as follows. In Section 2, we establish several new comparison principles, which play an important role in the proof of main results. Further, to study the nonlinear problem (1.1), we consider the associated linear problem and obtain the uniqueness of the solutions to the associated linear problem. In Section 3, the main theorems are formulated and proved. In Section 4, we give an example about integral boundary value problem for impulsive functional integrodifferential equations of mixed type (1.1).
2. Several Comparison Principles and Linear Problem
Lemma 2.1 (comparison result).
Assume that  satisfies
satisfies

where  ,
,  ,
,  ,
,  satisfy
satisfy
 ,
,
 ;
;
here

Then  ,
,  .
.
Proof.
Supposing that contrary (i.e.,  for some
for some  ), we consider the following two possible cases:
), we consider the following two possible cases:
(1) for all
for all  ;
;
(2)there exist  such that
such that  and
and  .
.
Let  ; we have
; we have

Case 1.
Equation (2.3) implies that  for
for  and
and  , hence,
, hence,  is nondecreasing on
is nondecreasing on  . By (2.3), we can get
. By (2.3), we can get

Integrating the above inequality from 0 to  , we have
, we have

Thus,

Noting condition (i), we have  . Besides,
. Besides,  , that is,
, that is, . Since
. Since  is nondecreasing on
is nondecreasing on  , then we have
, then we have  , for all
, for all  . That is,
. That is,  , for all
, for all  .
.
Case 2.
Firstly, we consider (2.3). Let  , then
, then  , and for some
, and for some  , there exists a
, there exists a  , such that
, such that  or
or  . We only consider
. We only consider  , for the case
, for the case  , and the proof is similar.
, and the proof is similar.
By (2.3), we have

Let  in (2.7); we have
in (2.7); we have

So,

On the other hand,

Let  in (2.10), then
in (2.10), then

That is,

By (2.3), we have

Thus, by (2.9), (2.13), and  , we obtain
, we obtain

So,  , which contradicts condition (ii). Hence,
, which contradicts condition (ii). Hence,  on
on  .
.
The proof of Lemma 2.1 is complete.
Corollary 2.2.
Assume that  ,
,  ,
,  ,
,  , and condition (ii) in Lemma 2.1 hold. Let
, and condition (ii) in Lemma 2.1 hold. Let  satisfy (2.1). Then
satisfy (2.1). Then  ,
,  .
.
Proof.
The proof of Corollary 2.2 is easy, so we omit it.
Lemma 2.3 (comparison result).
Let  satisfy (2.1). Assume that
satisfy (2.1). Assume that  ,
,  ,
,  and condition (i) in Lemma 2.1 hold. In addition assume that
and condition (i) in Lemma 2.1 hold. In addition assume that
 .
.
Then  ,
,  .
.
Proof.
The proof is similar to the proof of Lemma 2.1 [28], so we omit it.
Corollary 2.4.
Assume that  ,
,  ,
,  ,
,  , and condition (iii) in Lemma 2.3 hold. Let
, and condition (iii) in Lemma 2.3 hold. Let  satisfy (2.1). Then
satisfy (2.1). Then  ,
,  .
.
Proof.
The proof of Corollary 2.4 is easy, so we omit it.
Remark 2.5.
Corollary 2.4 holds for  if we delete
if we delete  .
.
Remark 2.6.
In the special case where (2.1) does not contain the operators  and
and  , Lemmas 2.1 and 2.3 develop Lemma 2.1 [28], and Corollaries 2.2 and 2.4 develop Corollary 2.1 [28]. Moreover, the condition
, Lemmas 2.1 and 2.3 develop Lemma 2.1 [28], and Corollaries 2.2 and 2.4 develop Corollary 2.1 [28]. Moreover, the condition  in Lemma 2.1 and Corollary 2.2 is more extensive than the corresponding condition in [28], and if we let
in Lemma 2.1 and Corollary 2.2 is more extensive than the corresponding condition in [28], and if we let  in Lemma 2.3 and Corollary 2.4, we can obtain Lemma 2.1 and Corollary 2.1 in [28], respectively. Therefore, our comparison results in this paper develop and generalize the corresponding results in [28].
in Lemma 2.3 and Corollary 2.4, we can obtain Lemma 2.1 and Corollary 2.1 in [28], respectively. Therefore, our comparison results in this paper develop and generalize the corresponding results in [28].
To study the nonlinear problem (1.1), we first consider the associated linear problem

where  ,
,  .
.
Definition 2.7.
One says  is a solution of (2.15) if it satisfies (2.15).
is a solution of (2.15) if it satisfies (2.15).
Definition 2.8.
One says that  is called a lower solution of (2.15) if
is called a lower solution of (2.15) if

and it is an upper solution of (2.15) if the above inequalities are reversed.
Lemma 2.9.
Let all assumptions of Lemma 2.1 hold. In addition assume that  are lower and upper solutions of (2.15), respectively, and
are lower and upper solutions of (2.15), respectively, and  , for all
, for all  . Then the problem (2.15) has a unique solution
. Then the problem (2.15) has a unique solution  .
.
Proof.
The proof is similar to the proof of Lemma 2.2 [28], so we omit it.
Remark 2.10.
In Lemma 2.9, if we replace "Lemma 2.1" by any of "Corollary 2.2", "Lemma 2.3", or "Corollary 2.4", then the conclusion of Lemma 2.9 holds.
3. Nonlinear Problem
Definition 3.1.
One says  is a solution of (1.1) if it satisfies (1.1).
is a solution of (1.1) if it satisfies (1.1).
Definition 3.2.
One says that  is called a lower solution of (1.1) if
is called a lower solution of (1.1) if

and it is an upper solution of (1.1) if the above inequalities are reversed.
Theorem 3.3.
Let all assumptions of Lemma 2.1 hold. In addition assume that
 are lower and upper solutions of (1.1), respectively, and
are lower and upper solutions of (1.1), respectively, and  , for all
, for all  ;
;
the function  satisfies
satisfies

for  ,
,  ,
,  ,
,  , for all
, for all  ;
;
the function  satisfies
satisfies

for  ,
,  ;
;
there exists  such that
such that

if  .
.
Then there exist monotone iterative sequences  ,
,  , which converge uniformly on
, which converge uniformly on  to the extremal solutions of (1.1) in
to the extremal solutions of (1.1) in  :
:  .
.
Proof.
For any  , we consider the problem
, we consider the problem

where

Firstly, we verify that  ,
,  are lower and upper solutions in the reversed order of (3.5). By
are lower and upper solutions in the reversed order of (3.5). By  , we obtain, for
, we obtain, for  ,
,

and, analogously,

Besides, for  ,
,

In addition,

Therefore,  ,
,  are lower and upper solutions in the reversed order of (3.5). By Lemma 2.9, we know that (3.5) has a unique solution
are lower and upper solutions in the reversed order of (3.5). By Lemma 2.9, we know that (3.5) has a unique solution  .
.
Now, we prove that  . Let
. Let  ; we can get
; we can get

By Lemma 2.1, we have that  , for all
, for all  . That is,
. That is,  . Similarly, we can show that
. Similarly, we can show that  . Therefore, we have
. Therefore, we have  .
.
Next, we denote an operator  by
by  . We prove that
. We prove that  is nondecreasing. Let
is nondecreasing. Let  such that
such that  . Setting
. Setting  , by
, by  , we have
, we have

By Lemma 2.1, we know  on
on  , that is,
, that is,  is nondecreasing.
is nondecreasing.
Now, let  ,
,  ,
,  , then we have
, then we have

Obviously,  satisfy
satisfy

with  defined by
defined by

Therefore, there exist  ,
,  such that
such that

uniformly on  , and the limit functions
, and the limit functions  ,
,  satisfy (1.1). Moreover,
satisfy (1.1). Moreover,  .
.
Finally, we prove that  ,
,  are the extremal solutions of (1.1) in
are the extremal solutions of (1.1) in  . Let
. Let  be any solution of (1.1), then
be any solution of (1.1), then  . By
. By  and the properties of
and the properties of  , we have
, we have

Thus, taking limit in (3.17) as  , we have
, we have  . That is,
. That is,  ,
,  are the extremal solutions of (1.1) in
are the extremal solutions of (1.1) in  .
.
The proof of Theorem 3.3 is complete.
Theorem 3.4.
Let conditions  and all assumptions of any of Corollary 2.2, Lemma 2.3, or Corollary 2.4 satisfy, then the conclusion of Theorem 3.3 hold.
and all assumptions of any of Corollary 2.2, Lemma 2.3, or Corollary 2.4 satisfy, then the conclusion of Theorem 3.3 hold.
Proof.
The proof is similar to the proof of Theorem 3.3, so we omit it.
4. Example
Consider the integral boundary value problem

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , for all
, for all  .
.
Obviously,  ,
,  are lower and upper solutions of (4.1), respectively, and
are lower and upper solutions of (4.1), respectively, and  .
.
Note that  ,
,  , and
, and  .
.
We have

where  ,
,  ,
,  ,
,  , for all
, for all  .
.
For  ,
,  ,
,  ,
,  ,
,  ,
,  , it is easy to verify that all conditions of Theorem 3.3 hold. Therefore, by Theorem 3.3, there exist monotone iterative sequences
, it is easy to verify that all conditions of Theorem 3.3 hold. Therefore, by Theorem 3.3, there exist monotone iterative sequences  ,
,  , which converge uniformly on
, which converge uniformly on  to the extremal solutions of (4.1) in
to the extremal solutions of (4.1) in  .
.
Remark 4.1.
For appropriate and suitable choices of  ,
,  ,
,  , and
, and  , we see that problem (4.1) has a very general form. For example, we can take
, we see that problem (4.1) has a very general form. For example, we can take  ,
,  ,
, , and
, and  .
.
5. Conclusions
In this paper, we have discussed the integral boundary value problem for first-order impulsive functional integrodifferential equations with deviating arguments under the assumption of existing upper and lower solutions in the reversed order. The main results (Theorems 3.3 and 3.4) are new and the following results appear as its special cases.
(i)If we take  in (1.1), we obtain the first-order impulsive ordinary integrodifferential equations with integral boundary conditions.
in (1.1), we obtain the first-order impulsive ordinary integrodifferential equations with integral boundary conditions.
(ii)By taking  and
and  in (1.1), our result corresponds to periodic boundary value problem for first-order impulsive functional integrodifferential equations with deviating arguments.
in (1.1), our result corresponds to periodic boundary value problem for first-order impulsive functional integrodifferential equations with deviating arguments.
(iii)For  ,
,  , in (1.1), we get the integral boundary value problem for first-order mixed type integrodifferential equations with deviating arguments.
, in (1.1), we get the integral boundary value problem for first-order mixed type integrodifferential equations with deviating arguments.
References
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Guo D, Lakshmikantham V, Liu XZ: Nonlinear Integral Equations in Abstract Spaces, Mathematics and Its Applications. Volume 373. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:viii+341.
Bainov DD, Simeonov PS: Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical, Harlow, UK; 1993.
Benchohra M, Henderson J, Ntouyas S: Impulsive Differential Equations and Inclusions, Contemporary Mathematics and Its Applications. Volume 2. Hindawi Publishing Corporation, New York, NY, USA; 2006:xiv+366.
Ahmad B, Alsaedi A, Alghamdi BS: Analytic approximation of solutions of the forced Duffing equation with integral boundary conditions. Nonlinear Analysis: Real World Applications 2008,9(4):1727-1740. 10.1016/j.nonrwa.2007.05.005
Jiang J, Liu L, Wu Y: Second-order nonlinear singular Sturm-Liouville problems with integral boundary conditions. Applied Mathematics and Computation 2009,215(4):1573-1582. 10.1016/j.amc.2009.07.024
Zhang X, Feng M, Ge W: Existence result of second-order differential equations with integral boundary conditions at resonance. Journal of Mathematical Analysis and Applications 2009,353(1):311-319. 10.1016/j.jmaa.2008.11.082
Jankowski T: Positive solutions for fourth-order differential equations with deviating arguments and integral boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2010,73(5):1289-1299. 10.1016/j.na.2010.04.055
Wang G: Boundary value problems for systems of nonlinear integro-differential equations with deviating arguments. Journal of Computational and Applied Mathematics 2010,234(5):1356-1363. 10.1016/j.cam.2010.01.009
Wang G, Song G, Zhang Lihong: Integral boundary value problems for first order integro-differential equations with deviating arguments. Journal of Computational and Applied Mathematics 2009,225(2):602-611. 10.1016/j.cam.2008.08.030
Wang G, Zhang L, Song G: Mixed boundary value problems for second order differential equations with different deviated arguments. Journal of Applied Mathematics & Informatics 2011,29(1-2):191-200.
Wang G, Zhang L, Song G: Integral boundary value problem for impulsive integro-differential equations in Banach spaces. Journal of Applied Mathematics and Computing. In press
Wang G, Zhang L, Song G: Systems of first order impulsive functional differential equations with deviating arguments and nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2011,74(3):974-982. 10.1016/j.na.2010.09.054
Franco D, Nieto JJ: First-order impulsive ordinary differential equations with anti-periodic and nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2000,42(2):163-173. 10.1016/S0362-546X(98)00337-X
Nieto JJ, Rodríguez-López R: Boundary value problems for a class of impulsive functional equations. Computers & Mathematics with Applications 2008,55(12):2715-2731. 10.1016/j.camwa.2007.10.019
Ahmad B, Nieto JJ: Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3291-3298. 10.1016/j.na.2007.09.018
Liang R, Shen J: Periodic boundary value problem for the first order impulsive functional differential equations. Journal of Computational and Applied Mathematics 2007,202(2):498-510. 10.1016/j.cam.2006.03.017
Yang X, Shen J: Nonlinear boundary value problems for first order impulsive functional differential equations. Applied Mathematics and Computation 2007,189(2):1943-1952. 10.1016/j.amc.2006.12.085
Luo Z, Jing Z: Periodic boundary value problem for first-order impulsive functional differential equations. Computers & Mathematics with Applications 2008,55(9):2094-2107.
He Z, He X: Periodic boundary value problems for first order impulsive integro-differential equations of mixed type. Journal of Mathematical Analysis and Applications 2004,296(1):8-20. 10.1016/j.jmaa.2003.12.047
Jankowski T: Four-point boundary-value problems for differential-algebraic systems. Journal of Optimization Theory and Applications 2010,144(1):56-68. 10.1007/s10957-009-9587-3
Jankowski T: First-order impulsive ordinary differential equations with advanced arguments. Journal of Mathematical Analysis and Applications 2007,331(1):1-12. 10.1016/j.jmaa.2006.07.108
Dyki A, Jankowski T: Boundary value problems for ordinary differential equations with deviated arguments. Journal of Optimization Theory and Applications 2007,135(2):257-269. 10.1007/s10957-007-9248-3
Li J, Shen J: Periodic boundary value problems for delay differential equations with impulses. Journal of Computational and Applied Mathematics 2006,193(2):563-573. 10.1016/j.cam.2005.05.037
Ehme J, Eloe PW, Henderson J: Upper and lower solution methods for fully nonlinear boundary value problems. Journal of Differential Equations 2002,180(1):51-64. 10.1006/jdeq.2001.4056
Nieto JJ, Rodríguez-López R: Remarks on periodic boundary value problems for functional differential equations. Journal of Computational and Applied Mathematics 2003,158(2):339-353. 10.1016/S0377-0427(03)00452-7
Wang W, Yang X, Shen J: Boundary value problems involving upper and lower solutions in reverse order. Journal of Computational and Applied Mathematics 2009,230(1):1-7. 10.1016/j.cam.2008.10.040
Wang G, Zhang L, Song G: Extremal solutions for the first order impulsive functional differential equations with upper and lower solutions in reversed order. Journal of Computational and Applied Mathematics 2010,235(1):325-333. 10.1016/j.cam.2010.06.014
Cabada A, Habets P, Pouso RL:Optimal existence conditions for
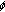 -Laplacian equations with upper and lower solutions in the reversed order. Journal of Differential Equations 2000,166(2):385-401. 10.1006/jdeq.2000.3803
-Laplacian equations with upper and lower solutions in the reversed order. Journal of Differential Equations 2000,166(2):385-401. 10.1006/jdeq.2000.3803Cabada A, Otero-Espinar V:Existence and comparison results for difference
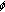 -Laplacian boundary value problems with lower and upper solutions in reverse order. Journal of Mathematical Analysis and Applications 2002,267(2):501-521. 10.1006/jmaa.2001.7783
-Laplacian boundary value problems with lower and upper solutions in reverse order. Journal of Mathematical Analysis and Applications 2002,267(2):501-521. 10.1006/jmaa.2001.7783Cabada A, Grossinho MR, Minhós F: Extremal solutions for third-order nonlinear problems with upper and lower solutions in reversed order. Nonlinear Analysis: Theory, Methods & Applications 2005,62(6):1109-1121. 10.1016/j.na.2005.04.023
Jiang D, Yang Y, Chu J, O'Regan D: The monotone method for Neumann functional differential equations with upper and lower solutions in the reverse order. Nonlinear Analysis: Theory, Methods & Applications 2007,67(10):2815-2828. 10.1016/j.na.2006.09.042
Li F, Jia M, Liu X, Li C, Li G: Existence and uniqueness of solutions of second-order three-point boundary value problems with upper and lower solutions in the reversed order. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2381-2388. 10.1016/j.na.2007.01.065
Acknowledgments
The aouthors would like to express their gratitude to the anonymous reviewers and editors for their valuable comments and suggestions which led to the improvement of the original paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, G., Zhang, L. & Song, G. New Existence Results and Comparison Principles for Impulsive Integral Boundary Value Problem with Lower and Upper Solutions in Reversed Order. Adv Differ Equ 2011, 783726 (2011). https://doi.org/10.1155/2011/783726
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/783726
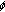 -Laplacian equations with upper and lower solutions in the reversed order. Journal of Differential Equations 2000,166(2):385-401. 10.1006/jdeq.2000.3803
-Laplacian equations with upper and lower solutions in the reversed order. Journal of Differential Equations 2000,166(2):385-401. 10.1006/jdeq.2000.3803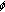 -Laplacian boundary value problems with lower and upper solutions in reverse order. Journal of Mathematical Analysis and Applications 2002,267(2):501-521. 10.1006/jmaa.2001.7783
-Laplacian boundary value problems with lower and upper solutions in reverse order. Journal of Mathematical Analysis and Applications 2002,267(2):501-521. 10.1006/jmaa.2001.7783