- Research Article
- Open access
- Published:
Weighted Inequalities for Potential Operators with Lipschitz and BMO Norms
Advances in Difference Equations volume 2011, Article number: 659597 (2011)
Abstract
Some Lipschitz norm and BMO norm inequalities for potential operator to the versions of differential forms are obtained, and some properties of a new kind of  weight are derived.
weight are derived.
1. Introduction
In many situations, the process to study solutions of PDEs involves estimating the various norms of the operators. Hence, we are motivated to establish some Lipschitz norm inequalities and BMO norm inequalities for potential operator to the versions of differential forms.
We keep using the traditional notation.
Let  be a connected open subset of
be a connected open subset of  , let
, let  be the standard unit basis of
be the standard unit basis of  , and let
, and let  be the linear space of
be the linear space of  -covectors, spanned by the exterior products
-covectors, spanned by the exterior products  , corresponding to all ordered
, corresponding to all ordered  -tuples
-tuples  ,
, ,
,  . We let
. We let  . The Grassman algebra
. The Grassman algebra  is a graded algebra with respect to the exterior products. For
is a graded algebra with respect to the exterior products. For  and
and  , the inner product in
, the inner product in  is given by
is given by  with summation over all
with summation over all  -tuples
-tuples  and all integers
and all integers  . We define the Hodge star operator
. We define the Hodge star operator  :
:  by the rule
by the rule  and
and  for all
for all  . The norm of
. The norm of  is given by the formula
is given by the formula  . The Hodge star is an isometric isomorphism on
. The Hodge star is an isometric isomorphism on  with
with  :
:  and
and  :
:  . Balls are denoted by
. Balls are denoted by  , and
, and  is the ball with the same center as
is the ball with the same center as  and with
and with  . We do not distinguish balls from cubes throughout this paper. The
. We do not distinguish balls from cubes throughout this paper. The  -dimensional Lebesgue measure of a set
-dimensional Lebesgue measure of a set  is denoted by
is denoted by  . We call
. We call  a weight if
a weight if  and that is,
and that is,  . For
. For  and a weight
and a weight  , we denote the weighted
, we denote the weighted  -norm of a measurable function
-norm of a measurable function  over
over  by
by

where  is a real number.
is a real number.
Differential forms are important generalizations of real functions and distributions; note that a 0-form is the usual function in  . A differential
. A differential  -form
-form  on
on  is a Schwartz distribution on
is a Schwartz distribution on  with values in
with values in  . We use
. We use  to denote the space of all differential
to denote the space of all differential  -forms
-forms  . We write
. We write  for the
for the  -forms with
-forms with  for all ordered
for all ordered  -tuples
-tuples  . Thus,
. Thus,  is a Banach space with norm
is a Banach space with norm

For  , the vector-valued differential form
, the vector-valued differential form  consists of differential forms
consists of differential forms  , where the partial differentiations are applied to the coefficients of
, where the partial differentiations are applied to the coefficients of  . As usual,
. As usual,  is used to denote the Sobolev space of
is used to denote the Sobolev space of  -forms, which equals
-forms, which equals 
 with norm
with norm

The notations  and
and  are self-explanatory. For
are self-explanatory. For  and a weight
and a weight  , the weighted norm of
, the weighted norm of  over
over  is denoted by
is denoted by

where  is a real number. We denote the exterior derivative by
is a real number. We denote the exterior derivative by  :
:  for
for  . Its formal adjoint operator
. Its formal adjoint operator  :
:  is given by
is given by  on
on  .
.
Let  . We write
. We write  if
if

for some  . Further, we write
. Further, we write  for those forms whose coefficients are in the usual Lipschitz space with exponent
for those forms whose coefficients are in the usual Lipschitz space with exponent  and write
and write  for this norm. Similarly, for
for this norm. Similarly, for  , we write
, we write  if
if

for some  . When
. When  is a 0-form, (1.6) reduces to the classical definition of
is a 0-form, (1.6) reduces to the classical definition of  .
.
Based on the above results, we discuss the weighted Lipschitz and BMO norms. For  , we write
, we write  if
if

for some  , where
, where  is a bounded domain, the Radon measure
is a bounded domain, the Radon measure  is defined by
is defined by  is a weight and
is a weight and  is a real number. For convenience, we will write the following simple notation
is a real number. For convenience, we will write the following simple notation  for
for  . Similarly, for
. Similarly, for  , we write
, we write  if
if

for some  , where the Radon measure
, where the Radon measure  is defined by
is defined by  is a weight, and
is a weight, and  is a real number. Again, we use
is a real number. Again, we use  to replace
to replace  whenever it is clear that the integral is weighted.
whenever it is clear that the integral is weighted.
From [1], if  is a differential form defined in a bounded, convex domain
is a differential form defined in a bounded, convex domain  , then there is a decomposition
, then there is a decomposition

where  is called a homotopy operator. Furthermore, we can define the
is called a homotopy operator. Furthermore, we can define the  -form
-form  by
by

for all  .
.
For any differential  -form
-form  , we define the potential operator
, we define the potential operator  by
by

where the kernel  is a nonnegative measurable function defined for
is a nonnegative measurable function defined for  , and the summation is over all ordered
, and the summation is over all ordered  -tuples
-tuples  . It is easy to find that the case
. It is easy to find that the case  reduces to the usual potential operator. That is,
reduces to the usual potential operator. That is,

where  is a function defined on
is a function defined on  . Associated with
. Associated with  , the functional
, the functional  is defined as
is defined as

where  is some sufficiently small constant and
is some sufficiently small constant and  is a ball with radius
is a ball with radius  . Throughout this paper, we always suppose that
. Throughout this paper, we always suppose that  satisfies the following conditions: there exists
satisfies the following conditions: there exists  such that
such that

and there exists  such that
such that

On the potential operator  and the functional
and the functional  , see [2] for details.
, see [2] for details.
The nonlinear elliptic partial differential equation  is called the homogeneous
is called the homogeneous  -harmonic equation or the
-harmonic equation or the  -harmonic equation, and the differential equation
-harmonic equation, and the differential equation

is called the nonhomogeneous  -harmonic equation for differential forms, where
-harmonic equation for differential forms, where  :
:  and
and  :
:  satisfy the conditions
satisfy the conditions

for almost every  and all
and all  . Here
. Here  are constants and
are constants and  is a fixed exponent associated with (1.16). A solution to (1.16) is an element of the Sobolev space
is a fixed exponent associated with (1.16). A solution to (1.16) is an element of the Sobolev space  such that
such that

for all  with compact support. When
with compact support. When  is a 0-form, that is,
is a 0-form, that is,  is a function, (1.16) is equivalent to
is a function, (1.16) is equivalent to

Lots of results have been obtained in recent years about different versions of the  -harmonic equation, see [3–5].
-harmonic equation, see [3–5].
2. The Estimate for Potential Operators with Lipschitz Norm and BMO Norm
In this section, we give the estimate for potential operators with Lipschitz norm and BMO norm applied to differential forms. The following strong type  inequality for potential operators appears in [6].
inequality for potential operators appears in [6].
Lemma 2.1 (see [6]).
Let  , be a differential form defined in a bounded, convex domain
, be a differential form defined in a bounded, convex domain  , and let
, and let  be coefficient of
be coefficient of  with
with  for all ordered
for all ordered  -tuples
-tuples  . Assume that
. Assume that  and
and  is the potential operator with
is the potential operator with  for any
for any  , then there exists a constant
, then there exists a constant  , independent of
, independent of  , such that
, such that

We will establish the following estimate for potential operators.
Theorem 2.2.
Let  , be a differential form defined in a bounded, convex domain
, be a differential form defined in a bounded, convex domain  , and let
, and let  be coefficient of
be coefficient of  with
with  for all ordered
for all ordered  -tuples
-tuples  . Assume that
. Assume that  and
and  is the potential operator with
is the potential operator with  for any
for any  , then there exists a constant
, then there exists a constant  , independent of
, independent of  , such that
, such that

Proof.
By the definition of the Lipschitz norm, (2.1), and hölder's inequality with  , we have
, we have

since  and
and  , where
, where  is a constant and
is a constant and  .
.
By the definition of the BMO norm, we have

We have completed the proof of Theorem 2.2.
3. The 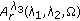 Weight
Weight
In this section, we introduce the  weight appeared in [7].
weight appeared in [7].
Definition 3.1.
Let  be two locally integrable nonnegative functions in
be two locally integrable nonnegative functions in  and assume that
and assume that  almost everywhere. We say that
almost everywhere. We say that  belongs to the
belongs to the  class,
class,  and
and  , or that
, or that  is an
is an  weight, write
weight, write  or
or  when it will not cause any confusion, if
when it will not cause any confusion, if

for all balls  .
.
The following results show that the  weights have the properties similar to those of the
weights have the properties similar to those of the  weights.
weights.
Theorem 3.2.
If  , then
, then  .
.
Proof.
Let  . Since
. Since  , by Hölder's inequality,
, by Hölder's inequality,

so that

Thus, we find that

for all balls  since
since  . Therefore,
. Therefore,  , and hence
, and hence  .
.
Theorem 3.3.
If  and the measures
and the measures  are defined by
are defined by  , then
, then

where  is a ball in
is a ball in  and
and  is a measurable subset of
is a measurable subset of  .
.
Proof.
By Hölder's inequality, we have

This implies

Note that  , by Hölder's inequality again, we have
, by Hölder's inequality again, we have

so that

Hence, we obtain

Since  , there exists a constant
, there exists a constant  such that
such that

Combining (3.7), (3.10), and (3.11), we deduce that

Hence,

The desired result is obtained.
If we choose  and
and  in Theorem 3.3, we will obtain
in Theorem 3.3, we will obtain

which is called the strong doubling property of  weights; see [8].
weights; see [8].
4. The Weighted Inequality for Potential Operators
In this section, we are devoted to develop some two-weight norm inequalities for potential operator  to the versions of differential forms. We need the following lemmas.
to the versions of differential forms. We need the following lemmas.
Lemma 4.1 (see [9]).
If  , then there exist constants
, then there exist constants  and
and  , independent of
, independent of  , such that
, such that

for all balls  .
.
Lemma 4.2.
Let  ,
,  , and
, and  . If
. If  and
and  are measurable functions on
are measurable functions on  , then
, then

for any  .
.
Lemma 4.3 (see [10]).
Let  be a solution of the nonhomogeneous A-harmonic equation in
be a solution of the nonhomogeneous A-harmonic equation in  and
and  , then there exists a constant
, then there exists a constant  , independent of
, independent of  , such that
, such that

for all  with
with  .
.
Theorem 4.4.
Let  , be a solution of the nonhomogeneous
, be a solution of the nonhomogeneous  -harmonic equation (1.16) in a bounded domain
-harmonic equation (1.16) in a bounded domain  and
and  is the potential operator with
is the potential operator with  for any
for any  , where the Radon measures
, where the Radon measures  and
and  are defined by
are defined by  . Assume that
. Assume that  and
and  for some
for some  with
with  for any
for any  , then there exists a constant
, then there exists a constant  , independent of
, independent of  , such that
, such that

where  is a constant with
is a constant with  .
.
Proof.
Since  , using Lemma 4.1, there exist constants
, using Lemma 4.1, there exist constants  and
and  , such that
, such that

for any ball  .
.
Since  , by Lemma 4.2, we have
, by Lemma 4.2, we have

Choose  where
where  ,
,  , then
, then  and
and  . Since
. Since  , by Lemma 4.2 and (4.5), we have
, by Lemma 4.2 and (4.5), we have

From Lemma 2.1, we have

Applying Lemma 4.3 (the weak reverse Hölder inequality for the solutions of the nonhomogeneous  -harmonic equation), we obtain
-harmonic equation), we obtain

where  is a constant and
is a constant and  . Choosing
. Choosing  , then
, then  . Using Hölder's inequality with
. Using Hölder's inequality with  , we have
, we have

Since  , then
, then

Since  , combining with (4.6)–(4.11), we have
, combining with (4.6)–(4.11), we have

From the definition of the BMO norm, we obtain

for all balls  with
with  and
and  . We have completed the proof of Theorem 4.4.
. We have completed the proof of Theorem 4.4.
References
Agarwal RP, Ding S, Nolder C: Inequalities for Differential Forms. Springer, New York, NY, USA; 2009:xvi+387.
Martell JM: Fractional integrals, potential operators and two-weight, weak type norm inequalities on spaces of homogeneous type. Journal of Mathematical Analysis and Applications 2004,294(1):223-236. 10.1016/j.jmaa.2004.02.012
Gao H:Weighted integral inequalities for conjugate
 -harmonic tensors. Journal of Mathematical Analysis and Applications 2003,281(1):253-263.
-harmonic tensors. Journal of Mathematical Analysis and Applications 2003,281(1):253-263.Gao H, Qiao J, Chu Y: Local regularity and local boundedness results for very weak solutions of obstacle problems. Journal of Inequalities and Applications 2010, 2010:-12.
Gao H, Qiao J, Wang Y, Chu Y: Local regularity results for minima of anisotropic functionals and solutions of anisotropic equations. Journal of Inequalities and Applications 2008, 2008:-11.
Bi H: Weighted inequalities for potential operators on differential forms. Journal of Inequalities and Applications 2010, 2010:-13.
Tong Y, Li J, Gu J:
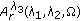 -weighted inequalities with Lipschitz and BMO norms. Journal of Inequalities and Applications 2010, 2010:-13.
-weighted inequalities with Lipschitz and BMO norms. Journal of Inequalities and Applications 2010, 2010:-13.Heinonen J, Kilpeläinen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. The Clarendon Press Oxford University Press, New York, NY, USA; 1993:vi+363.
Garnett JB: Bounded Analytic Functions, Pure and Applied Mathematics. Volume 96. Academic Press, New York, NY, USA; 1981:xvi+467.
Nolder CA:Hardy-Littlewood theorems for
 -harmonic tensors. Illinois Journal of Mathematics 1999,43(4):613-632.
-harmonic tensors. Illinois Journal of Mathematics 1999,43(4):613-632.
Acknowledgments
The authors are supported by NSF of Hebei Province (A2010000910) and Scientific Research Fund of Zhejiang Provincial Education Department (Y201016044).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tong, Y., Gu, J. Weighted Inequalities for Potential Operators with Lipschitz and BMO Norms. Adv Differ Equ 2011, 659597 (2011). https://doi.org/10.1155/2011/659597
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/659597
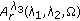 Weight
Weight -harmonic tensors. Journal of Mathematical Analysis and Applications 2003,281(1):253-263.
-harmonic tensors. Journal of Mathematical Analysis and Applications 2003,281(1):253-263.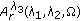 -weighted inequalities with Lipschitz and BMO norms. Journal of Inequalities and Applications 2010, 2010:-13.
-weighted inequalities with Lipschitz and BMO norms. Journal of Inequalities and Applications 2010, 2010:-13. -harmonic tensors. Illinois Journal of Mathematics 1999,43(4):613-632.
-harmonic tensors. Illinois Journal of Mathematics 1999,43(4):613-632.