- Research Article
- Open access
- Published:
Composition Theorems of Stepanov Almost Periodic Functions and Stepanov-Like Pseudo-Almost Periodic Functions
Advances in Difference Equations volume 2011, Article number: 654695 (2011)
Abstract
We establish a composition theorem of Stepanov almost periodic functions, and, with its help, a composition theorem of Stepanov-like pseudo almost periodic functions is obtained. In addition, we apply our composition theorem to study the existence and uniqueness of pseudo-almost periodic solutions to a class of abstract semilinear evolution equation in a Banach space. Our results complement a recent work due to Diagana (2008).
1. Introduction
Recently, in [1, 2], Diagana introduced the concept of Stepanov-like pseudo-almost periodicity, which is a generalization of the classical notion of pseudo-almost periodicity, and established some properties for Stepanov-like pseudo-almost periodic functions. Moreover, Diagana studied the existence of pseudo-almost periodic solutions to the abstract semilinear evolution equation  . The existence theorems obtained in [1, 2] are interesting since
. The existence theorems obtained in [1, 2] are interesting since  is only Stepanov-like pseudo-almost periodic, which is different from earlier works. In addition, Diagana et al. [3] introduced and studied Stepanov-like weighted pseudo-almost periodic functions and their applications to abstract evolution equations.
is only Stepanov-like pseudo-almost periodic, which is different from earlier works. In addition, Diagana et al. [3] introduced and studied Stepanov-like weighted pseudo-almost periodic functions and their applications to abstract evolution equations.
On the other hand, due to the work of [4] by N'Guérékata and Pankov, Stepanov-like almost automorphic problems have widely been investigated. We refer the reader to [5–11] for some recent developments on this topic.
Since Stepanov-like almost-periodic (almost automorphic) type functions are not necessarily continuous, the study of such functions will be more difficult considering complexity and more interesting in terms of applications.
Very recently, in [12], Li and Zhang obtained a new composition theorem of Stepanov-like pseudo-almost periodic functions; the authors in [13] established a composition theorem of vector-valued Stepanov almost-periodic functions. Motivated by [2, 12, 13], in this paper, we will make further study on the composition theorems of Stepanov almost-periodic functions and Stepanov-like pseudo-almost periodic functions. As one will see, our main results extend and complement some results in [2, 13].
Throughout this paper, let  be the set of real numbers, let
be the set of real numbers, let  be the Lebesgue measure for any subset
be the Lebesgue measure for any subset  , and
, and  be two arbitrary real Banach spaces. Moreover, we assume that
be two arbitrary real Banach spaces. Moreover, we assume that  if there is no special statement. First, let us recall some definitions and basic results of almost periodic functions, Stepanov almost periodic functions, pseudo-almost periodic functions, and Stepanov-like pseudo-almost periodic functions (for more details, see [2, 14, 15]).
if there is no special statement. First, let us recall some definitions and basic results of almost periodic functions, Stepanov almost periodic functions, pseudo-almost periodic functions, and Stepanov-like pseudo-almost periodic functions (for more details, see [2, 14, 15]).
Definition 1.1.
A set  is called relatively dense if there exists a number
is called relatively dense if there exists a number  such that
such that

Definition 1.2.
A continuous function  is called almost periodic if for each
is called almost periodic if for each  there exists a relatively dense set
there exists a relatively dense set  such that
such that

We denote the set of all such functions by  or
or  .
.
Definition 1.3.
A continuous function  is called almost periodic in
is called almost periodic in  uniformly for
uniformly for  if, for each
if, for each  and each compact subset
and each compact subset  , there exists a relatively dense set
, there exists a relatively dense set 

We denote by  the set of all such functions.
the set of all such functions.
Definition 1.4.
The Bochner transform  ,
,  ,
,  , of a function
, of a function  on
on  , with values in
, with values in  , is defined by
, is defined by

Definition 1.5.
The space  of all Stepanov bounded functions, with the exponent
of all Stepanov bounded functions, with the exponent  , consists of all measurable functions
, consists of all measurable functions  on
on  with values in
with values in  such that
such that

It is obvious that  and
and  whenever
whenever  .
.
Definition 1.6.
A function  is called Stepanov almost periodic if
is called Stepanov almost periodic if  ; that is, for all
; that is, for all  , there exists a relatively dense set
, there exists a relatively dense set  such that
such that

We denote the set of all such functions by  or
or  .
.
Remark 1.7.
It is clear that  for
for  .
.
Definition 1.8.
A function  with
with  , for each
, for each  , is called Stepanov almost periodic in
, is called Stepanov almost periodic in  uniformly for
uniformly for  if, for each
if, for each  and each compact set
and each compact set  , there exists a relatively dense set
, there exists a relatively dense set  such that
such that

for each  and each
and each  . We denote by
. We denote by  the set of all such functions.
the set of all such functions.
It is also easy to show that  for
for  .
.
Throughout the rest of this paper, let  (resp.,
(resp.,  ) be the space of bounded continuous (resp., jointly bounded continuous) functions with supremum norm, and
) be the space of bounded continuous (resp., jointly bounded continuous) functions with supremum norm, and

We also denote by  the space of all functions
the space of all functions  such that
such that

uniformly for  in any compact set
in any compact set  .
.
Definition 1.9.
A function  is called pseudo-almost periodic if
is called pseudo-almost periodic if

with  and
and  . We denote by
. We denote by  the set of all such functions.
the set of all such functions.
It is well-known that  is a closed subspace of
is a closed subspace of  , and thus
, and thus  is a Banach space under the supremum norm.
is a Banach space under the supremum norm.
Definition 1.10.
A function  is called Stepanov-like pseudo-almost periodic if it can be decomposed as
is called Stepanov-like pseudo-almost periodic if it can be decomposed as  with
with  and
and  . We denote the set of all such functions by
. We denote the set of all such functions by  or
or  .
.
It follows from [2] that  for all
for all  .
.
Definition 1.11.
A function  with
with  , for each
, for each  , is called Stepanov-like pseud-almost periodic in
, is called Stepanov-like pseud-almost periodic in  uniformly for
uniformly for  if it can be decomposed as
if it can be decomposed as  with
with  and
and  . We denote by
. We denote by  the set of all such functions.
the set of all such functions.
Next, let us recall some notations about evolution family and exponential dichotomy. For more details, we refer the reader to [16].
Definition 1.12.
A set  of bounded linear operator on
of bounded linear operator on  is called an evolution family if
is called an evolution family if
-
(a)
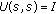 ,
, 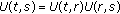 for
for 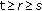 and
and  ,
, -
(b)
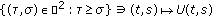 is strongly continuous.
is strongly continuous.
Definition 1.13.
An evolution family  is called hyperbolic (or has exponential dichotomy) if there are projections
is called hyperbolic (or has exponential dichotomy) if there are projections  ,
,  , being uniformly bounded and strongly continuous in
, being uniformly bounded and strongly continuous in  , and constants
, and constants  ,
,  such that
such that
-
(a)
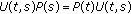 for all
for all  ,
, -
(b)
the restriction
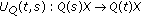 is invertible for all
is invertible for all 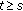
 ,
, -
(c)
 and
and  for all
for all 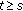 ,
,where
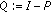 . We call that
. We call that (1.11)
(1.11)is the Green's function corresponding to
 and
and 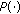 .
.
Remark 1.14.
Exponential dichotomy is a classical concept in the study of long-term behaviour of evolution equations; see, for example, [16]. It is easy to see that

2. Main Results
Throughout the rest of this paper, for  , we denote by
, we denote by  the set of all the functions
the set of all the functions  satisfying that there exists a function
satisfying that there exists a function  such that
such that

and, for any compact set  , we denote by
, we denote by  the set of all the functions
the set of all the functions  such that (1.7) is replaced by
such that (1.7) is replaced by

In addition, we denote by  the norm of
the norm of  and
and  .
.
Lemma 2.1.
Let  ,
,  be compact, and
be compact, and  . Then
. Then  .
.
Proof.
For all  , there exist
, there exist  such that
such that

Since  , for the above
, for the above  , there exists a relatively dense set
, there exists a relatively dense set  such that
such that

for all  ,
,  , and
, and  . On the other hand, since
. On the other hand, since  , there exists a function
, there exists a function  such that (2.1) holds.
such that (2.1) holds.
Fix  ,
,  . For each
. For each  , there exists
, there exists  such that
such that  . Thus, we have
. Thus, we have

for each  and
and  , which gives that
, which gives that

Now, by Minkowski's inequality and (2.4), we get

which means that  .
.
Theorem 2.2.
Assume that the following conditions hold:
-
(a)
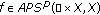 with
with  , and
, and  with
with  .
. -
(b)
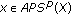 , and there exists a set
, and there exists a set 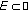 with
with  such that
such that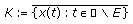 (2.8)
(2.8)is compact in
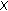 .
.
Then there exists  such that
such that  .
.
Proof.
Since  , there exists
, there exists  such that
such that  . Let
. Let

Then  and
and  . On the other hand, since
. On the other hand, since  , there is a function
, there is a function  such that (2.1) holds.
such that (2.1) holds.
It is easy to see that  is measurable. By using (2.1), for each
is measurable. By using (2.1), for each  , we have
, we have

Thus,  .
.
Next, let us show that  . By Lemma 2.1,
. By Lemma 2.1,  . In addition, we have
. In addition, we have  . Thus, for all
. Thus, for all  , there exists a relatively dense set
, there exists a relatively dense set  such that
such that

for all  and
and  . By using (2.11), we deduce that
. By using (2.11), we deduce that

for all  and
and  . Thus,
. Thus,  .
.
Lemma 2.3.
Let  be compact,
be compact,  , and
, and  . Then
. Then  , where
, where

Proof.
Noticing that  is a compact set, for all
is a compact set, for all  , there exist
, there exist  such that
such that

Combining this with  , for all
, for all  , there exists
, there exists  such that
such that

for all  and
and  . Thus, we get
. Thus, we get

which yields that

On the other hand, since  , for the above
, for the above  , there exists
, there exists  such that, for all
such that, for all  ,
,

This together with (2.17) implies that

Hence,  .
.
Theorem 2.4.
Assume that  and the following conditions hold:
and the following conditions hold:
-
(a)
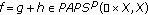 with
with 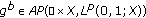 and
and  . Moreover,
. Moreover, 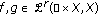 with
with 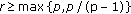 ;
; -
(b)
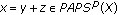 with
with 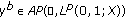 and
and 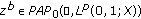 , and there exists a set
, and there exists a set  with
with  such that
such that (2.20)
(2.20)is compact in
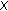 .
.
Then there exists  such that
such that  .
.
Proof.
Let  be as in the proof of Theorem 2.2. In addition, let
be as in the proof of Theorem 2.2. In addition, let  , where
, where

It follows from Theorem 2.2 that  , that is,
, that is,  .
.
Next, let us show that  . For
. For  , we have
, we have

where  was used. For
was used. For  , since
, since  , by Lemma 2.3, we know that
, by Lemma 2.3, we know that

which yields

that is,  . Now, we get
. Now, we get  .
.
Next, let us discuss the existence and uniqueness of pseudo-almost periodic solutions for the following abstract semilinear evolution equation in  :
:

Theorem 2.5.
Assume that  and the following conditions hold:
and the following conditions hold:
-
(a)
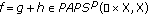 with
with 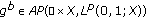 and
and  . Moreover,
. Moreover,  with
with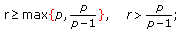 (2.26)
(2.26) -
(b)
the evolution family
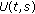 generated by
generated by 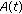 has an exponential dichotomy with constants
has an exponential dichotomy with constants 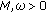 , dichotomy projections
, dichotomy projections 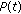 ,
, 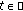 , and Green's function
, and Green's function  ;
; -
(c)
for all
 , for all
, for all  , and for all
, and for all 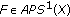 there exists a relatively dense set
there exists a relatively dense set 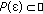 such that
such that 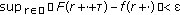 and
and 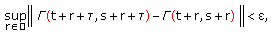 (2.27)
(2.27)
for all  and
and  with
with  .
.
Then (2.25) has a unique pseudo-almost periodic mild solution provided that

Proof.
Let  , where
, where  and
and  . Then
. Then  and
and  is compact in
is compact in  . By the proof of Theorem 2.4, there exists
. By the proof of Theorem 2.4, there exists  such that
such that  .
.
Let

where  and
and  . Denote
. Denote

where

By [13, Theorem 2.3] we have  . In addition, by a similar proof to that of [2, Theorem 3.2], one can obtain that
. In addition, by a similar proof to that of [2, Theorem 3.2], one can obtain that  . So
. So  maps
maps  into
into  . For
. For  , by using the Hölder's inequality, we obtain
, by using the Hölder's inequality, we obtain

for all  , which yields that
, which yields that  has a unique fixed point
has a unique fixed point  and
and

This completes the proof.
Remark 2.6.
For some general conditions which can ensure that the assumption (c) in Theorem 2.5 holds, we refer the reader to [17, Theorem 4.5]. In addition, in the case of  and
and  generating an exponential stable semigroup
generating an exponential stable semigroup  , the assumption (c) obviously holds.
, the assumption (c) obviously holds.
References
Diagana T: Stepanov-like pseudo almost periodic functions and their applications to differential equations. Communications in Mathematical Analysis 2007,3(1):9-18.
Diagana T: Stepanov-like pseudo-almost periodicity and its applications to some nonautonomous differential equations. Nonlinear Analysis. Theory, Methods & Applications 2008,69(12):4277-4285. 10.1016/j.na.2007.10.051
Diagana T, Mophou GM, N'Guérékata GM:Existence of weighted pseudo-almost periodic solutions to some classes of differential equations with
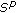 -weighted pseudo-almost periodic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2010,72(1):430-438. 10.1016/j.na.2009.06.077
-weighted pseudo-almost periodic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2010,72(1):430-438. 10.1016/j.na.2009.06.077N'Guérékata GM, Pankov A: Stepanov-like almost automorphic functions and monotone evolution equations. Nonlinear Analysis. Theory, Methods & Applications 2008,68(9):2658-2667. 10.1016/j.na.2007.02.012
Diagana T:Existence of pseudo-almost automorphic solutions to some abstract differential equations with
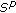 -pseudo-almost automorphic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034
-pseudo-almost automorphic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034Diagana T: Existence of almost automorphic solutions to some classes of nonautonomous higher-order differential equations. Electronic Journal of Qualitative Theory of Differential Equations 2010, 22: 1-26.
Ding H-S, Liang J, Xiao T-J: Almost automorphic solutions to nonautonomous semilinear evolution equations in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2010,73(5):1426-1438. 10.1016/j.na.2010.05.006
Ding H-S, Liang J, Xiao T-J: Some properties of Stepanov-like almost automorphic functions and applications to abstract evolution equations. Applicable Analysis 2009,88(7):1079-1091. 10.1080/00036810903156164
Fan ZB, Liang J, Xiao TJ: On Stepanov-like (pseudo) almost automorphic functions. Nonlinear Analysis: Theory, Methods and Applications 2011,74(8):2853-2861. 10.1016/j.na.2011.01.007
Fan ZB, Liang J, Xiao TJ: Composition of Stepanov-like pseudo almost automorphic functions and applications to nonautonomous evolution equations. preprint
Ding H-S, Liang J, Xiao T-J: Almost automorphic solutions to abstract fractional differential equations. Advances in Difference Equations 2010, 2010:-9.
Li H-X, Zhang L-L: Stepanov-like pseudo-almost periodicity and semilinear differential equations with uniform continuity. Results in Mathematics 2011,59(1-2):43-61. 10.1007/s00025-010-0050-4
Ding HS, Long W, N'Guérékata GM: Almost periodic solutions to abstract semilinear evolutionequations with Stepanov almost periodic coeffcient. Journal of Computational Analysis and Applications 2011, 13: 231-243.
Pankov AA: Bounded and Almost Periodic Solutions of Nonlinear Operator Differential Equations. Volume 55. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:x+221.
Levitan BM, Zhikov VV: Almost Periodic Functions and Differential Equations. Cambridge University Press, Cambridge, UK; 1982:xi+211.
Engel K-J, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000:xxii+586.
Maniar L, Schnaubelt R: Almost periodicity of inhomogeneous parabolic evolution equations. In Evolution Equations. Volume 234. Marcel Dekker, New York, NY, USA; 2003:299-318.
Acknowledgments
The work was supported by the NSF of China, the Key Project of Chinese Ministry of Education, the NSF of Jiangxi Province of China, the Youth Foundation of Jiangxi Provincial Education Department (GJJ09456), and the Youth Foundation of Jiangxi Normal University (2010-96).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Long, W., Ding, HS. Composition Theorems of Stepanov Almost Periodic Functions and Stepanov-Like Pseudo-Almost Periodic Functions. Adv Differ Equ 2011, 654695 (2011). https://doi.org/10.1155/2011/654695
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/654695
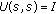 ,
, 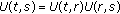 for
for 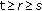 and
and  ,
,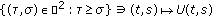 is strongly continuous.
is strongly continuous.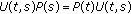 for all
for all  ,
,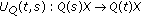 is invertible for all
is invertible for all 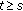
 ,
, and
and  for all
for all 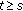 ,
,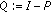 . We call that
. We call that
 and
and 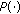 .
.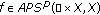 with
with  , and
, and  with
with  .
.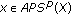 , and there exists a set
, and there exists a set 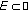 with
with  such that
such that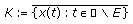
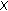 .
.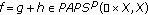 with
with 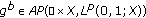 and
and  . Moreover,
. Moreover, 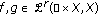 with
with 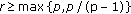 ;
;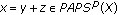 with
with 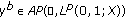 and
and 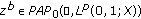 , and there exists a set
, and there exists a set  with
with  such that
such that
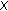 .
.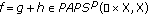 with
with 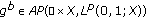 and
and  . Moreover,
. Moreover,  with
with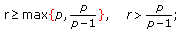
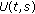 generated by
generated by 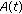 has an exponential dichotomy with constants
has an exponential dichotomy with constants 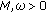 , dichotomy projections
, dichotomy projections 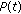 ,
, 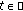 , and Green's function
, and Green's function  ;
; , for all
, for all  , and for all
, and for all 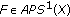 there exists a relatively dense set
there exists a relatively dense set 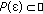 such that
such that 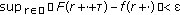 and
and 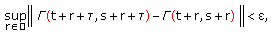
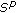 -weighted pseudo-almost periodic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2010,72(1):430-438. 10.1016/j.na.2009.06.077
-weighted pseudo-almost periodic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2010,72(1):430-438. 10.1016/j.na.2009.06.077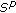 -pseudo-almost automorphic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034
-pseudo-almost automorphic coefficients. Nonlinear Analysis. Theory, Methods & Applications 2009,70(11):3781-3790. 10.1016/j.na.2008.07.034