- Research Article
- Open access
- Published:
Impulsive Integrodifferential Equations Involving Nonlocal Initial Conditions
Advances in Difference Equations volume 2011, Article number: 634701 (2011)
Abstract
We focus on a Cauchy problem for impulsive integrodifferential equations involving nonlocal initial conditions, where the linear part is a generator of a solution operator on a complex Banach space. A suitable mild solution for the Cauchy problem is introduced. The existence and uniqueness of mild solutions for the Cauchy problem, under various criterions, are proved. In the last part of the paper, we construct an example to illustrate the feasibility of our results.
1. Introduction
Let  denote a complex Banach space and denote
denote a complex Banach space and denote  by the space of all bounded linear operators from
by the space of all bounded linear operators from  into
into  with the usual operator norm
with the usual operator norm  . Let us recall the following definitions.
. Let us recall the following definitions.
Definition 1.1 (see [1]).
Let  be a continuous function and
be a continuous function and  . Then the expression
. Then the expression

is called the Riemann-Liouville integral of order  .
.
Definition 1.2 (see [2]).
Let  be a linear and closed operator with domain
be a linear and closed operator with domain  defined on
defined on  . By a solution operator associated with
. By a solution operator associated with  in
in  , we mean a family
, we mean a family  of strongly continuous operators satisfying
of strongly continuous operators satisfying
-
(1)
 and
and -
(2)
 (1.2)
(1.2)where
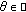 is a constant and
is a constant and 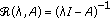 stands for the resolvent of
stands for the resolvent of 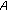 . In this case, we also say that
. In this case, we also say that  is a solution operator generated by
is a solution operator generated by  .
.
Remark 1.3.
It is to be noted that in the border case  , the family
, the family  corresponds to a classical strongly continuous semigroup, whereas in the case
corresponds to a classical strongly continuous semigroup, whereas in the case  a solution operator corresponds to the concept of a cosine family. Moreover, according to [3], one can find that solution operators are a particular case of
a solution operator corresponds to the concept of a cosine family. Moreover, according to [3], one can find that solution operators are a particular case of  -regularized families and a solution operator
-regularized families and a solution operator  corresponds to a
corresponds to a  -regularized family.
-regularized family.
Remark 1.4.
Note that solution operator  does not satisfy the semigroup property.
does not satisfy the semigroup property.
Remark 1.5.
Various solution operators are usually key tools in dealing with the abstract Cauchy problems and related issues. For more information, please see, for example, [4–11] and references therein.
Starting from some speculations of Leibniz and Euler, the fractional calculus (such as the Riemann-Liouville fractional integral) which allows us to consider integration and differentiation of any order, not necessarily integer, have been the object of extensive study for analyzing not only stochastic processes driven by fractional Brownian motion, but also nonrandom fractional phenomena in physics and optimal control (cf. e.g., [1, 12, 13]). One of the emerging branches of the study is the Cauchy problems of abstract differential equations involving fractional integration or fractional differentiation (see, e.g., [1, 14–17]). Let us point out that many phenomena in engineering, physics, economy, chemistry, aerodynamics, and electrodynamics of complex medium can be modeled by this class of equations.
In the present paper we study the existence and uniqueness of mild solutions for the Cauchy problem for impulsive integrodifferential equations involving nonlocal initial conditions in the form

where  ,
,  is a generator of a solution operator
is a generator of a solution operator  ,
,  ,
,  and
and  stand for the right and left limits of
stand for the right and left limits of  at
at  , respectively, and
, respectively, and  ,
,  are appropriate functions to be specified later. As can be seen, the convolution integral in (1.3) is the Riemann-Liouville fractional integral, and the function
are appropriate functions to be specified later. As can be seen, the convolution integral in (1.3) is the Riemann-Liouville fractional integral, and the function  constitutes a nonlocal condition.
constitutes a nonlocal condition.
As usual, the solution  with the points of discontinuity at the moments
with the points of discontinuity at the moments  follows that
follows that  , that is, at which it is continuous from the left.
, that is, at which it is continuous from the left.
We mention that in recent years, the theory of various integrodifferential equations in Banach spaces has been studied deeply due to their important values in sciences and technologies, and many significant results have been established (see, e.g., [2, 18–23] and references therein).
Interest in impulsive nonlocal Cauchy problems stems mainly from the observation that on one side, nonlocal initial conditions have better effects in treating physical problems than the usual ones (see [21, 22, 24–27] and the references therein for more detailed information about the importance of nonlocal initial conditions in applications); on the other side, the dynamics of many evolutionary processes from some research fields are subject to abrupt changes of states at certain moments of time between intervals of continuous evolution, such changes can be well approximated as being instantaneous changes as state, that is, in the form of "impulses" (cf. [20, 28] and the references therein). This class of equations has been the object of extensive study in recent years, see [29–31] and the references therein for more comments and citations. It is worth mentioning that in [31], Liang et al. considered the following impulsive nonlocal Cauchy problem

where  is the generator of a strongly continuous semigroup in a Banach space and the existence and uniqueness of mild and classical solutions for the Cauchy problem, under various criterions, are proved. Also, Wang et al. [32] proved the existence and uniqueness of mild and classical solutions for the nonlocal Cauchy problem in the form
is the generator of a strongly continuous semigroup in a Banach space and the existence and uniqueness of mild and classical solutions for the Cauchy problem, under various criterions, are proved. Also, Wang et al. [32] proved the existence and uniqueness of mild and classical solutions for the nonlocal Cauchy problem in the form

where  ,
,  is a
is a  -almost sectorial operator (not necessarily densely defined).
-almost sectorial operator (not necessarily densely defined).
In this work, motivated by the above contributions, we shall combine these earlier work and extend the study to the Cauchy problem (1.3). New existence and uniqueness results in the case when  is a generator of a solution operator, under various criterions, are proved. In the last part of paper, we construct an example to illustrate the feasibility of our results.
is a generator of a solution operator, under various criterions, are proved. In the last part of paper, we construct an example to illustrate the feasibility of our results.
2. Preliminaries
Throughout this paper, we take  to be the Banach space of all
to be the Banach space of all  -valued continuous functions from
-valued continuous functions from  into
into  endowed with the uniform norm topology
endowed with the uniform norm topology

Put

with  ,
,  , and let
, and let  be the restriction of a function
be the restriction of a function  to
to  .
.
Consider the set of functions

endowed with the norm

It is easy to see  is a Banach space.
is a Banach space.
Let  . It follows from [33] that if
. It follows from [33] that if  is sectorial of type
is sectorial of type  , that is,
, that is,  is a closed linear operator, and there exist constants
is a closed linear operator, and there exist constants  and
and  such that
such that  and
and

then  is a generator of a solution operator
is a generator of a solution operator  , which is given by
, which is given by

provided that  , where
, where  is a suitable path lying outside the sector
is a suitable path lying outside the sector  . And Cuesta [18, Theorem 1], has proved that if
. And Cuesta [18, Theorem 1], has proved that if  is a sectorial operator of type
is a sectorial operator of type  and there is a positive constant
and there is a positive constant  which depends on
which depends on  such that the estimate
such that the estimate

holds for all  .
.
We recall that the Laplace transform of a abstract function  is defined by
is defined by

We first treat the following problem:

Formally applying the Laplace transform in (2.9), we obtain

which establishes the following result:

This means that

Motivated by the above consideration, we give the following definition.
Definition 2.1.
Let  . A solution
. A solution  of the integral equation
of the integral equation

is called a mild solution of the following problem:

where  is the solution operator generated by
is the solution operator generated by  .
.
We list the following basic assumptions of this paper.
 is continuous in
is continuous in  on
on  and there exists a constant
and there exists a constant  such that
such that

for all  .
.
 is continuous and there exists a function
is continuous and there exists a function  such that
such that

for all  .
.
 is completely continuous and there exists a continuous nondecreasing function
is completely continuous and there exists a continuous nondecreasing function  such that for each
such that for each  ,
,

 is Lipschitz continuous with Lipschitz constant
is Lipschitz continuous with Lipschitz constant  .
.
For  ,
,  is Lipschitz continuous with Lipschitz constant
is Lipschitz continuous with Lipschitz constant  .
.
For  ,
,  is completely continuous and there exists a continuous nondecreasing function
is completely continuous and there exists a continuous nondecreasing function  such that for each
such that for each  ,
,

The following fixed-point theorem plays a key role in the proof of our main results.
Lemma 2.2 (see [34]).
Let  be a convex, bounded, and closed subset of a Banach space
be a convex, bounded, and closed subset of a Banach space  and let
and let  be a condensing map. Then,
be a condensing map. Then,  has a fixed point in
has a fixed point in  .
.
3. Main Results
To set the framework for our main existence results, we will make use of the following lemma.
Lemma 3.1.
Let  . Assume that
. Assume that  is a sectorial operator of type
is a sectorial operator of type  and
and  is a solution operator generated by
is a solution operator generated by  . Suppose in addition that
. Suppose in addition that  is a continuous function. If
is a continuous function. If  is a mild solution of the Cauchy problem (2.14) in the sense of Definition 2.1, then,
is a mild solution of the Cauchy problem (2.14) in the sense of Definition 2.1, then,  satisfying the following impulsive integral equation:
satisfying the following impulsive integral equation:

is a mild solution of problem (1.3), where


Proof.
Assume that  is a mild solution of (2.14) in the sense of Definition 2.1. Obviously, if
is a mild solution of (2.14) in the sense of Definition 2.1. Obviously, if  , then one sees from Definition 2.1, that the assertion of theorem remains true. Thus, the rest proof of the theorem is done under
, then one sees from Definition 2.1, that the assertion of theorem remains true. Thus, the rest proof of the theorem is done under  .
.
By Definition 2.1, note that

for all  . Taking
. Taking  , then we get
, then we get

Hence, it follows form  that
that

If  , then combining Definition 2.1 and the result above, we deduce that
, then combining Definition 2.1 and the result above, we deduce that

This proves, for the case  , that the conclusion of theorem holds.
, that the conclusion of theorem holds.
Now taking  in (3.7), one has
in (3.7), one has

which implies that

provided that  . Then, again making use of Definition 2.1, we get for all
. Then, again making use of Definition 2.1, we get for all  ,
,

here  and
and  are given by (3.2) and (3.3) with
are given by (3.2) and (3.3) with  , respectively. A continuation of the same process shows that for any
, respectively. A continuation of the same process shows that for any  , the assertion of theorem holds.
, the assertion of theorem holds.
In this work, we adopt the following concept of mild solution for the problem (1.3).
Definition 3.2.
Let  . Assume that
. Assume that  is a sectorial operator of type
is a sectorial operator of type  ,
,  is a solution operator generated by
is a solution operator generated by  , and
, and  and
and  are given by (3.2) and (3.3), respectively. A solution
are given by (3.2) and (3.3), respectively. A solution  of the integral equation
of the integral equation

here  , is called a mild solution of the Cauchy problem (1.3).
, is called a mild solution of the Cauchy problem (1.3).
Remark 3.3.
Note that if there is no discontinuity, that is, if  ,
,  , then Definition 2.1 is equivalent to Definition 3.2.
, then Definition 2.1 is equivalent to Definition 3.2.
Now we present and prove our main results.
Theorem 3.4.
Let  . Assume that
. Assume that  is a sectorial operator of type
is a sectorial operator of type  and
and  is a solution operator generated by
is a solution operator generated by  . Suppose in addition that assumptions
. Suppose in addition that assumptions  are fulfilled. Then the Cauchy problem (1.3) admits at least one mild solution, provided
are fulfilled. Then the Cauchy problem (1.3) admits at least one mild solution, provided

Proof.
Consider the mapping  , which is defined for each
, which is defined for each  by
by

Then it is clear that  is well defined.
is well defined.
To prove the theorem, it is sufficient to prove that  has a fixed point in
has a fixed point in  .
.
Put

for  as selected below.
as selected below.
We first show that there exists an integer  such that
such that  maps
maps  into
into  . For the case
. For the case  , by assumption
, by assumption  and the estimate (2.7), a straightforward calculation yields that
and the estimate (2.7), a straightforward calculation yields that

We claim that there exists an integer  such that
such that  provided that
provided that  . In fact, if this is not the case, then for each
. In fact, if this is not the case, then for each  , there would exist
, there would exist  and
and  such that
such that  . Thus, by (3.15) and assumption
. Thus, by (3.15) and assumption  we obtain
we obtain

Dividing on both sides by  and taking the lower limit as
and taking the lower limit as  , we get
, we get

which contradicts (3.12).
Since the interval  is divided into finite subintervals by
is divided into finite subintervals by  , we only need to prove that for a fixed
, we only need to prove that for a fixed  ,
,

maps  into
into  , here
, here  is a positive number yet to be determined, as the cases for other subintervals are the same.
is a positive number yet to be determined, as the cases for other subintervals are the same.
From the Hypotheses  , we infer for any
, we infer for any  ,
,

Now, an application of the same idea with above discussion yields that there exists a  such that
such that  . Indeed, if this is not the case, then we would deduce that
. Indeed, if this is not the case, then we would deduce that

This is a contradiction to (3.12). Thus, we prove that there exists an integer  such that
such that  .
.
For  , we decompose the mapping
, we decompose the mapping  as follows:
as follows:

Next, we show that for each  ,
,  is completely continuous, while
is completely continuous, while  is a contraction. In fact, it follows from assumption
is a contraction. In fact, it follows from assumption  and the estimate (2.7) that
and the estimate (2.7) that  ,
,  is completely continuous. Note also that
is completely continuous. Note also that

For the case  , it is clear that the conclusion holds in view of (3.12). For
, it is clear that the conclusion holds in view of (3.12). For  , by
, by  ,
,  and (2.7) we get
and (2.7) we get

provided that  . Hence, we deduce that
. Hence, we deduce that

which means that  is a contraction due to (3.12).
is a contraction due to (3.12).
Thus,  is a condensing map on
is a condensing map on  . Then, it follows from Lemma 2.2 that the Cauchy problem (1.3) admits at least one mild solution. This completes the proof.
. Then, it follows from Lemma 2.2 that the Cauchy problem (1.3) admits at least one mild solution. This completes the proof.
Theorem 3.5.
Let  . Assume that
. Assume that  is a sectorial operator of type
is a sectorial operator of type  ,
,  is a solution operator generated by
is a solution operator generated by  , and the Hypotheses
, and the Hypotheses  are satisfied. Then the Cauchy problem (1.3) admits at least one mild solution, provided
are satisfied. Then the Cauchy problem (1.3) admits at least one mild solution, provided

Proof.
Assume that the map  and the set
and the set  are defined the same as in Theorem 3.4. First we claim that there exists an positive number
are defined the same as in Theorem 3.4. First we claim that there exists an positive number  such that
such that  . For the case
. For the case  , the proof of the assertion follows from Theorem 3.4. For the case
, the proof of the assertion follows from Theorem 3.4. For the case  , if the conclusion is not true, then for each positive integer
, if the conclusion is not true, then for each positive integer  , there would exist
, there would exist  and
and  such that
such that  with
with  , where
, where  denotes
denotes  depending upon
depending upon  . Thus, by assumptions
. Thus, by assumptions  ,
,  ,
,  , we have
, we have

Dividing on both sides by  and taking the lower limit as
and taking the lower limit as  , we have
, we have

This is a contradiction to (3.25).
For  , decompose the mapping
, decompose the mapping  as follows:
as follows:

Next, we will verify that for each  ,
,  is a completely continuous operator, while,
is a completely continuous operator, while,  is a contraction. Obviously, by assumptions
is a contraction. Obviously, by assumptions  , it easily seen that
, it easily seen that  is a completely continuous operator. Moreover, by a similar proof with that in Theorem 3.4, we can prove that
is a completely continuous operator. Moreover, by a similar proof with that in Theorem 3.4, we can prove that  is a contraction.
is a contraction.
As a consequence of the above discussion and Lemma 2.2, we can conclude that the problem (1.3) admits at least one mild solution. The proof is completed.
Theorem 3.6.
Let  . Assume that
. Assume that  is a sectorial operator of type
is a sectorial operator of type  and
and  is a solution operator generated by
is a solution operator generated by  . Then, under assumptions
. Then, under assumptions  ,
,  ,
,  , the Cauchy problem (1.3) has a unique mild solution, provided
, the Cauchy problem (1.3) has a unique mild solution, provided

Proof.
Assume that the map  is defined the same as in Theorem 3.4. Now, we prove that
is defined the same as in Theorem 3.4. Now, we prove that  is a contraction. Take any
is a contraction. Take any  . For the case
. For the case  , the conclusion follows from assumptions
, the conclusion follows from assumptions  ,
,  , and (3.29). For
, and (3.29). For  , a direct calculation yields
, a direct calculation yields

in view of assumptions  ,
,  ,
,  . Hence, we deduce that
. Hence, we deduce that

which implies  is a contractive mapping on
is a contractive mapping on  due to (3.29). Thus
due to (3.29). Thus  has a unique fixed point
has a unique fixed point  , this means that
, this means that  is a mild solution of (1.3). This completes the proof of the theorem.
is a mild solution of (1.3). This completes the proof of the theorem.
4. Example
In this section, we present an example to illustrate the abstract results of this paper, which do not aim at generality but indicate how our theorems can be applied to concrete problems.
Consider the BVP of partial differential equation in the form

where  ,
,  is a constant in
is a constant in  ,
,  is a constant yet to be determined,
is a constant yet to be determined,  stands for the operator with respect to the spatial variable
stands for the operator with respect to the spatial variable  which is given by
which is given by

In what follows we consider the space with norm
with norm  and the operator
and the operator  with domain
with domain

Clearly  is densely defined in
is densely defined in  and is sectorial of type
and is sectorial of type . Hence
. Hence  is a generator of a solution operator satisfying the estimate (2.7) on
is a generator of a solution operator satisfying the estimate (2.7) on  . Here, without lost of generality, we take
. Here, without lost of generality, we take  .
.
Set

Then we have

Note that the problem (4.1) also can be reformulated as the abstract problem (1.3), and due to (4.5), it is not difficult to see that assumptions  ,
,  , and
, and  hold with
hold with

which implies that one can choose large enough  such that the first inequality of (3.29) is satisfied. Hence, according to Theorem 3.6, the Cauchy problem (4.1) has a unique mild solution.
such that the first inequality of (3.29) is satisfied. Hence, according to Theorem 3.6, the Cauchy problem (4.1) has a unique mild solution.
References
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Cuevas C, César de Souza J:Existence of
 -asymptotically
-asymptotically  -periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis. Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007
-periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis. Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007Lizama C: Regularized solutions for abstract Volterra equations. Journal of Mathematical Analysis and Applications 2000,243(2):278-292. 10.1006/jmaa.1999.6668
Batty CJK, Liang J, Xiao T-J: On the spectral and growth bound of semigroups associated with hyperbolic equations. Advances in Mathematics 2005,191(1):1-10. 10.1016/j.aim.2004.01.005
Engel K-J, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000:xxii+586.
Fattorini HO: Second Order Linear Differential Equations in Banach Spaces, North-Holland Mathematics Studies. Volume 108. North-Holland, Amsterdam, The Netherlands; 1985:xiii+314.
Liang J, Nagel R, Xiao T-J: Approximation theorems for the propagators of higher order abstract Cauchy problems. Transactions of the American Mathematical Society 2008,360(4):1723-1739.
Müller C: Solving abstract Cauchy problems with closable operators in reflexive spaces via resolvent-free approximation. Forum Mathematicum 2007,19(1):1-18. 10.1515/FORUM.2007.001
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: A solution to an open problem for wave equations with generalized Wentzell boundary conditions. Mathematische Annalen 2003,327(2):351-363. 10.1007/s00208-003-0457-2
Xiao T-J, Liang J: Complete second order differential equations in Banach spaces with dynamic boundary conditions. Journal of Differential Equations 2004,200(1):105-136. 10.1016/j.jde.2004.01.011
Anh VV, Leonenko NN: Spectral analysis of fractional kinetic equations with random data. Journal of Statistical Physics 2001,104(5-6):1349-1387.
Anh VV, Mcvinish R: Fractional differential equations driven by Lévy noise. Journal of Applied Mathematics and Stochastic Analysis 2003,16(2):97-119. 10.1155/S1048953303000078
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis. Theory, Methods & Applications 2008,60(10):3337-3343.
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis. Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Zhou Y, Jiao F: Existence of mild solutions for fractional neutral evolution equations. Computers & Mathematics with Applications 2010,59(3):1063-1077.
Zhou Y, Jiao F: Nonlocal Cauchy problem for fractional evolution equations. Nonlinear Analysis. Real World Applications 2010,11(5):4465-4475. 10.1016/j.nonrwa.2010.05.029
Cuesta E: Asymptotic behaviour of the solutions of fractional integro-differential equations and some time discretizations. Discrete and Continuous Dynamical Systems. Series A 2007, 277-285.
Ding H-S, Liang J, Xiao T-J: Positive almost automorphic solutions for a class of non-linear delay integral equations. Applicable Analysis 2009,88(2):231-242. 10.1080/00036810802713875
Guo DJ, Liu X: Extremal solutions of nonlinear impulsive integrodifferential equations in Banach spaces. Journal of Mathematical Analysis and Applications 1993,177(2):538-552. 10.1006/jmaa.1993.1276
Liang J, Liu JH, Xiao T-J: Nonlocal problems for integrodifferential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(6):815-824.
Liang J, Xiao T-J: Semilinear integrodifferential equations with nonlocal initial conditions. Computers & Mathematics with Applications 2004,47(6-7):863-875. 10.1016/S0898-1221(04)90071-5
Xiao T-J, Liang J, van Casteren J: Time dependent Desch-Schappacher type perturbations of Volterra integral equations. Integral Equations and Operator Theory 2002,44(4):494-506. 10.1007/BF01193674
Byszewski L: Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal Cauchy problem. Journal of Mathematical Analysis and Applications 1991,162(2):494-505. 10.1016/0022-247X(91)90164-U
Byszewski L, Lakshmikantham V: Theorem about the existence and uniqueness of a solution of a nonlocal abstract Cauchy problem in a Banach space. Applicable Analysis 1991,40(1):11-19. 10.1080/00036819008839989
Deng K: Exponential decay of solutions of semilinear parabolic equations with nonlocal initial conditions. Journal of Mathematical Analysis and Applications 1993,179(2):630-637. 10.1006/jmaa.1993.1373
Liang J, van Casteren J, Xiao T-J: Nonlocal Cauchy problems for semilinear evolution equations. Nonlinear Analysis. Theory, Methods & Applications 2002,50(2):173-189. 10.1016/S0362-546X(01)00743-X
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations. Volume 14. World Scientific Publishing, River Edge, NJ, USA; 1995:x+462.
Benchohra M, Gatsori EP, Henderson J, Ntouyas SK: Nondensely defined evolution impulsive differential inclusions with nonlocal conditions. Journal of Mathematical Analysis and Applications 2003,286(1):307-325. 10.1016/S0022-247X(03)00490-6
Fan ZB: Impulsive problems for semilinear differential equations with nonlocal conditions. Nonlinear Analysis. Theory, Methods & Applications 2010,72(2):1104-1109. 10.1016/j.na.2009.07.049
Liang J, Liu JH, Xiao T-J: Nonlocal impulsive problems for nonlinear differential equations in Banach spaces. Mathematical and Computer Modelling 2009,49(3-4):798-804. 10.1016/j.mcm.2008.05.046
Wang R-N, Li Z-Q, Ding X-H: Nonlocal Cauchy problems for semilinear evolution equations involving almost sectorial operators. Indian Journal of Pure and Applied Mathematics 2008,39(4):333-346.
Bajlekova EG: Fractional evolution equations in Banach spaces, Ph.D. thesis. Eindhoven University of Technology; 2001.
Sadovskiĭ BN: On a fixed point principle. Akademija Nauk SSSR 1967,1(2):74-76.
Acknowledgments
This research was supported in part by the NSF of JiangXi Province of China (2009GQS0018) and the Youth Foundation of JiangXi Provincial Education Department of China (GJJ10051).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, RN., Xia, J. Impulsive Integrodifferential Equations Involving Nonlocal Initial Conditions. Adv Differ Equ 2011, 634701 (2011). https://doi.org/10.1155/2011/634701
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/634701
 and
and
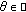 is a constant and
is a constant and 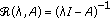 stands for the resolvent of
stands for the resolvent of 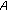 . In this case, we also say that
. In this case, we also say that  is a solution operator generated by
is a solution operator generated by  .
. -asymptotically
-asymptotically  -periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis. Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007
-periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis. Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007