- Research Article
- Open access
- Published:
Weighted 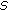 -Asymptotically
-Asymptotically  -Periodic Solutions of a Class of Fractional Differential Equations
-Periodic Solutions of a Class of Fractional Differential Equations
Advances in Difference Equations volume 2011, Article number: 584874 (2011)
Abstract
We study the existence of weighted  -asymptotically
-asymptotically  -periodic mild solutions for a class of abstract fractional differential equations of the form
-periodic mild solutions for a class of abstract fractional differential equations of the form  , where
, where  is a linear sectorial operator of negative type.
is a linear sectorial operator of negative type.
1. Introduction
 -asymptotically
-asymptotically  -periodic functions have applications to several problems, for example in the theory of functional differential equations, fractional differential equations, integral equations and partial differential equations. The concept of
-periodic functions have applications to several problems, for example in the theory of functional differential equations, fractional differential equations, integral equations and partial differential equations. The concept of  -asymptotic
-asymptotic  -periodicity was introduced in the literature by Henríquez et al. [1, 2]. Since then, it attracted the attention of many researchers (see [1–10]). In Pierri [10] a new
-periodicity was introduced in the literature by Henríquez et al. [1, 2]. Since then, it attracted the attention of many researchers (see [1–10]). In Pierri [10] a new  -asymptotically
-asymptotically  -periodic space was introduced. It is called the space of weighted
-periodic space was introduced. It is called the space of weighted  -asymptotically
-asymptotically  -periodic (or
-periodic (or  -asymptotically
-asymptotically  -periodic) functions. In particular, the author has established conditions under which a
-periodic) functions. In particular, the author has established conditions under which a  -asymptotically
-asymptotically  -periodic function is asymptotically
-periodic function is asymptotically  -periodic and also discusses the existence of
-periodic and also discusses the existence of  -asymptotically
-asymptotically  -periodic solutions for an integral abstract Cauchy problem. The author has applied the results to partial integrodifferential equations.
-periodic solutions for an integral abstract Cauchy problem. The author has applied the results to partial integrodifferential equations.
We study in this paper sufficient conditions for the existence and uniqueness of a weighted  -asymptotically
-asymptotically  -periodic (mild) solution to the following semi-linear integrodifferential equation of fractional order
-periodic (mild) solution to the following semi-linear integrodifferential equation of fractional order


where  ,
,  is a linear densely defined operator of sectorial type on a complex Banach space
is a linear densely defined operator of sectorial type on a complex Banach space  and
and  is an appropriate function. Note that the convolution integral in (1.1) is known as the Riemann-Liouville fractional integral [11]. We remark that there is much interest in developing theoretical analysis and numerical methods for fractional integrodifferential equations because they have recently proved to be valuable in various fields of sciences and engineering. For details, including some applications and recent results, see the monographs of Ahn and MacVinish [12], Gorenflo and Mainardi [13] and Trujillo et al. [14–16] and the papers of Agarwal et al. [17–23], Cuesta [11, 24], Cuevas et al. [5, 6], dos Santos and Cuevas [25], Eidelman and Kochubei [26], Lakshmikantham et al. [27–30], Mophou and N'Guérékata [31], Ahmed and Nieto [32], and N'Guérékata [33]. In particular equations of type (1.1) are attracting increasing interest (cf. [5, 11, 24, 34]).
is an appropriate function. Note that the convolution integral in (1.1) is known as the Riemann-Liouville fractional integral [11]. We remark that there is much interest in developing theoretical analysis and numerical methods for fractional integrodifferential equations because they have recently proved to be valuable in various fields of sciences and engineering. For details, including some applications and recent results, see the monographs of Ahn and MacVinish [12], Gorenflo and Mainardi [13] and Trujillo et al. [14–16] and the papers of Agarwal et al. [17–23], Cuesta [11, 24], Cuevas et al. [5, 6], dos Santos and Cuevas [25], Eidelman and Kochubei [26], Lakshmikantham et al. [27–30], Mophou and N'Guérékata [31], Ahmed and Nieto [32], and N'Guérékata [33]. In particular equations of type (1.1) are attracting increasing interest (cf. [5, 11, 24, 34]).
The existence of weighted  -asymptotically
-asymptotically  -periodic (mild) solutions for integrodifferential equation of fractional order of type (1.1) remains an untreated topic in the literature. Anticipating a wide interest in the subject, this paper contributes in filling this important gap. In particular, to illustrate our main results, we examine sufficient conditions for the existence and uniqueness of a weighted
-periodic (mild) solutions for integrodifferential equation of fractional order of type (1.1) remains an untreated topic in the literature. Anticipating a wide interest in the subject, this paper contributes in filling this important gap. In particular, to illustrate our main results, we examine sufficient conditions for the existence and uniqueness of a weighted  -asymptotically
-asymptotically  -periodic mild solution to a fractional oscillation equation.
-periodic mild solution to a fractional oscillation equation.
2. Preliminaries and Basic Results
In this section, we introduce notations, definitions and preliminary facts which are used throughout this paper. Let  and
and  be Banach spaces. The notation
be Banach spaces. The notation  stands for the space of bounded linear operators from
stands for the space of bounded linear operators from  into
into  endowed with the uniform operator topology denoted
endowed with the uniform operator topology denoted  , and we abbreviate to
, and we abbreviate to  and
and  whenever
whenever  . In this paper
. In this paper  denotes the Banach space consisting of all continuous and bounded functions from
denotes the Banach space consisting of all continuous and bounded functions from  into
into  with the norm of the uniform convergence. For a closed linear operator
with the norm of the uniform convergence. For a closed linear operator  we denote by
we denote by  the resolvent set and by
the resolvent set and by  the spectrum of
the spectrum of  (that is, the complement of
(that is, the complement of  in the complex plane). Set
in the complex plane). Set  the resolvent of
the resolvent of  for
for  .
.
2.1. Sectorial Linear Operators and the Solution Operator for Fractional Equations
A closed and linear operator  is said sectorial of type μ if there are
is said sectorial of type μ if there are  and
and  such that the spectrum of
such that the spectrum of  is contained in the sector
is contained in the sector  and
and  , for all
, for all  .
.
In order to give an operator theoretical approach for the study of the abstract system we recall the following definition.
Definition 2.1 (see [17]).
Let  be a closed linear operator with domain
be a closed linear operator with domain  in a Banach space
in a Banach space  . One calls
. One calls  the generator of a solution operator for (1.1)-(1.2) if there are
the generator of a solution operator for (1.1)-(1.2) if there are  and a strongly continuous function
and a strongly continuous function  such that
such that  and
and  , for all
, for all  . In this case,
. In this case,  is called the solution operator generated by
is called the solution operator generated by  . By [35, Proposition 2.6],
. By [35, Proposition 2.6],  . We observe that the power function
. We observe that the power function  is uniquely defined as
is uniquely defined as  , with
, with  .
.
We note that if  is a sectorial of type μ with
is a sectorial of type μ with  , then
, then  is the generator of a solution operator given by
is the generator of a solution operator given by  ,
,  , where
, where  is a suitable path lying outside the sector
is a suitable path lying outside the sector  (cf. [11]). Recently, Cuesta [11, Theorem 1] proved that if
(cf. [11]). Recently, Cuesta [11, Theorem 1] proved that if  is a sectorial operator of type
is a sectorial operator of type  for some
for some  and
and  , then there exists
, then there exists  such that
such that

Remark 2.2.
In the remainder of this paper, we always assume that  is a a sectorial of type
is a a sectorial of type  and
and  , are the constants introduced above.
, are the constants introduced above.
2.2. Weighted  -Asymptotically
-Asymptotically  -Periodic Functions
-Periodic Functions
We recall the following definitions.
Definition 2.3 (see [1]).
A function  is called
is called  -asymptotically
-asymptotically  -periodic if there exists
-periodic if there exists  such that
such that  . In this case, we say that
. In this case, we say that  is an asymptotic period of
is an asymptotic period of  .
.
Throughout this paper,  represents the space formed for all the
represents the space formed for all the  -valued
-valued  -asymptotically
-asymptotically  -periodic functions endowed with the uniform convergence norm denoted
-periodic functions endowed with the uniform convergence norm denoted  . It is clear that
. It is clear that  is a Banach space (see [1, Proposition 3.5]).
is a Banach space (see [1, Proposition 3.5]).
Definition 2.4 (see [10]).
Let  . A function
. A function  is called weighted
is called weighted  -asymptotically
-asymptotically  -periodic (or
-periodic (or  -asymptotically
-asymptotically  -periodic) if
-periodic) if  .
.
In this paper,  represents the space formed by all the
represents the space formed by all the  -asymptotically
-asymptotically  -periodic functions endowed with the norm
-periodic functions endowed with the norm

Proposition 2.5.
The space  is a Banach space.
is a Banach space.
Proof.
Let  be a Cauchy sequence in
be a Cauchy sequence in  . From the definition of
. From the definition of  , there exists
, there exists  such that
such that  in
in  . Next, we prove that
. Next, we prove that  in
in  .
.
By noting that  is a Cauchy sequence, for
is a Cauchy sequence, for  given there exists
given there exists  such that
such that  , for all
, for all  , which implies
, which implies

Under the above conditions, for  and
and  we see that
we see that

which implies that  for
for  and
and  as
as  .
.
To conclude the proof we need to show that  . Let
. Let  as above. Since
as above. Since  , there exits
, there exits  such that
such that  for all
for all  . Now, by using that
. Now, by using that  , for
, for  we get
we get

which implies that  . This completes the proof.
. This completes the proof.
Definition 2.6.
A function  is called uniformly
is called uniformly  -asymptotically
-asymptotically  -periodic on bounded sets if for every bounded subset
-periodic on bounded sets if for every bounded subset  , the set
, the set  is bounded and
is bounded and  , uniformly for
, uniformly for  . If
. If  we say that
we say that  is uniformly
is uniformly  -asymptotically
-asymptotically  -periodic on bounded sets (see [1]).
-periodic on bounded sets (see [1]).
To prove some of our results, we need the following lemma.
Lemma 2.7.
Let  . Assume
. Assume  is uniformly
is uniformly  -asymptotically
-asymptotically  -periodic on bounded sets and there is
-periodic on bounded sets and there is  such that
such that

If  , then the function
, then the function  belongs to
belongs to  .
.
Proof.
Using the fact that  is bounded, it follows that
is bounded, it follows that  . For
. For  be given, we select
be given, we select  such that
such that

for all  and
and  . Then, for
. Then, for  we see that
we see that

which proves the assertion.
Lemma 2.8.
Let  . Let
. Let  and
and  be the function defined by
be the function defined by

If  as
as  and
and  , then
, then  .
.
Proof.
From the estimate  , it follows that
, it follows that  . For
. For  be given we select
be given we select  such that
such that

for all  . Under these conditions, for
. Under these conditions, for  we have that
we have that

which completes the proof.
3. Existence of Weighted 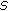 -Asymptotically
-Asymptotically  -Periodic Solutions
-Periodic Solutions
In this section we discuss the existence of weighted  -asymptotically
-asymptotically  -periodic solutions for the abstract system (1.1)-(1.2). To begin, we recall the definition of mild solution for (1.1)-(1.2).
-periodic solutions for the abstract system (1.1)-(1.2). To begin, we recall the definition of mild solution for (1.1)-(1.2).
Definition 3.1 (see [5]).
A function  is called a mild solution of the abstract Cauchy problem (1.1)-(1.2) if
is called a mild solution of the abstract Cauchy problem (1.1)-(1.2) if

Now, we can establish our first existence result.
Theorem 3.2.
Assume  is a uniformly
is a uniformly  -asymptotically
-asymptotically  -periodic on bounded sets function and there is a mesurable bounded function
-periodic on bounded sets function and there is a mesurable bounded function  such that
such that

If  , then there exits a unique
, then there exits a unique  -asymptotically
-asymptotically  -periodic mild solution
-periodic mild solution  of (1.1)-(1.2). Suppose, there is a function
of (1.1)-(1.2). Suppose, there is a function  such that
such that  and
and  , for every
, for every  and all
and all  . If
. If  is such that
is such that  as
as  , then
, then  is weighted
is weighted  -asymptotically
-asymptotically  -periodic.
-periodic.
Proof.
Let  be the operator defined by
be the operator defined by

We show initially that  is
is  -valued. Since
-valued. Since  , as
, as  , it is sufficient to show that the function
, it is sufficient to show that the function  is
is  -valued. Let
-valued. Let  . Using the fact that
. Using the fact that  is a bounded function, it follows that
is a bounded function, it follows that  . For
. For  be given, we select a constant
be given, we select a constant  such that
such that

Then, for  we see that
we see that

which implies that  as
as  ,
,  and hence
and hence  . Moreover, from the above estimate it is easy to infer that
. Moreover, from the above estimate it is easy to infer that  , for all
, for all  ,
,  is a contraction and there exists a unique
is a contraction and there exists a unique  -asymptotically
-asymptotically  -periodic mild solution
-periodic mild solution  of (1.1)-(1.2).
of (1.1)-(1.2).
Next, we prove that last assertion. Let  be the function defined by
be the function defined by  . For
. For  , we get
, we get

Concerning the quantities  and
and  , we note that
, we note that

Using the estimates (3.7) in (3.6), we see that

where  is a positive constant independent of
is a positive constant independent of  . Finally, by using the Gronwall-Bellman inequality we infer that
. Finally, by using the Gronwall-Bellman inequality we infer that

which shows that  . This completes the proof.
. This completes the proof.
Example 3.3.
We set  ,
,  with
with  . Let
. Let  be a function such that
be a function such that  , for all
, for all  and let
and let  be defined by
be defined by  ,
,  . We observe that
. We observe that

whence  is
is  -asymptotically
-asymptotically  -periodic on bounded sets. By Theorem 3.2 we conclude that if
-periodic on bounded sets. By Theorem 3.2 we conclude that if  , then there is a unique
, then there is a unique  -asymptotically
-asymptotically  -periodic mild solution
-periodic mild solution  of (1.1)-(1.2). Moreover
of (1.1)-(1.2). Moreover  .
.
Theorem 3.4.
Let  . Assume
. Assume  ,
,  as
as  and
and

where  is the constant introduced in Lemma 2.8.Then there is a unique weighted
is the constant introduced in Lemma 2.8.Then there is a unique weighted  -asymptotically
-asymptotically  -periodic mild solution of
-periodic mild solution of

Proof.
The proof is based in Lemmas 2.7 and 2.8. Let  be the map defined by
be the map defined by

We show initially that  is
is  -valued. From the estimate
-valued. From the estimate

we have that  .
.
Let  . From Lemma 2.7, we have that
. From Lemma 2.7, we have that  is a weighted
is a weighted  -asymptotically
-asymptotically  -periodic function and by Lemma 2.8 we obtain that
-periodic function and by Lemma 2.8 we obtain that  . Thus, the map
. Thus, the map  is
is  -valued. In order to prove that
-valued. In order to prove that  is a contraction, we note that for
is a contraction, we note that for  and
and  ,
,

so that,

On the another hand, for  we see that
we see that

from which we obtain that

By noting that  is a linear operator for all
is a linear operator for all  and combining (3.16) and (3.18) we obtain that
and combining (3.16) and (3.18) we obtain that

for all  , which shows that
, which shows that  is a contraction on
is a contraction on  and hence there is a unique
and hence there is a unique  -asymptotically
-asymptotically  -periodic mild solution. The proof is complete.
-periodic mild solution. The proof is complete.
To complete this paper, we examine the existence and uniqueness of weighted  -asymptotically
-asymptotically  -periodic mild solutions for the following fractional differential equation
-periodic mild solutions for the following fractional differential equation

with boundary conditions


where  and
and  . In what follows we consider the space
. In what follows we consider the space  and let
and let  be the operator given by
be the operator given by  with domain
with domain  ,
,  . It is well known that
. It is well known that  is sectorial of type negative.
is sectorial of type negative.
Proposition 3.5.
Let  satisfying conditions of Lemma 2.8 and let
satisfying conditions of Lemma 2.8 and let  . If
. If  is small enough, then the problems (3.20)–(3.22) has a unique
is small enough, then the problems (3.20)–(3.22) has a unique  -asymptotically
-asymptotically  -periodic mild solution.
-periodic mild solution.
Proof.
Problem (3.20)–(3.22) can be expressed as an abstract fractional differential equation of the form (3.12), where  , for
, for  . We define
. We define

We have the following estimates:


estimate (3.25), we get

Since  we obtain that
we obtain that  . Moreover, we have the inequality
. Moreover, we have the inequality

If we choose  small enough, we have that condition (3.11) is fulfilled. By Theorem 3.4, the problems (3.20)–(3.22) has a unique
small enough, we have that condition (3.11) is fulfilled. By Theorem 3.4, the problems (3.20)–(3.22) has a unique  -asymptotically
-asymptotically  -periodic (mild) solution. This finishes the proof.
-periodic (mild) solution. This finishes the proof.
References
Henríquez HR, Pierri M, Táboas P:On
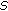 -asymptotically
-asymptotically  -periodic functions on Banach spaces and applications. Journal of Mathematical Analysis and Applications 2008,343(2):1119-1130. 10.1016/j.jmaa.2008.02.023
-periodic functions on Banach spaces and applications. Journal of Mathematical Analysis and Applications 2008,343(2):1119-1130. 10.1016/j.jmaa.2008.02.023Henríquez HR, Pierri M, Táboas P:Existence of
 -asymptotically
-asymptotically  -periodic solutions for abstract neutral equations. Bulletin of the Australian Mathematical Society 2008,78(3):365-382. 10.1017/S0004972708000713
-periodic solutions for abstract neutral equations. Bulletin of the Australian Mathematical Society 2008,78(3):365-382. 10.1017/S0004972708000713Agarwal RP, de Andrade B, Cuevas C: On type of periodicity and ergodicity to a class of integral equations with infinite delay. Journal of Nonlinear and Convex Analysis 2010,11(2):309-333.
Caicedo A, Cuevas C:
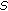 -asymptotically
-asymptotically  -periodic solutions of abstract partial neutral integro-differentail equations. Functional Differential Equations 2010,17(1-2):387-405.
-periodic solutions of abstract partial neutral integro-differentail equations. Functional Differential Equations 2010,17(1-2):387-405.Cuevas C, de Souza JC:
 -asymptotically
-asymptotically  -periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013
-periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013Cuevas C, César de Souza J:Existence of
 -asymptotically
-asymptotically  -periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007
-periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007Cuevas C, Lizama C:
 -asymptotically
-asymptotically  -periodic solutions for semilinear Volterra equations. Mathematical Methods in the Applied Sciences 2010,33(13):1628-1636.
-periodic solutions for semilinear Volterra equations. Mathematical Methods in the Applied Sciences 2010,33(13):1628-1636.de Andrade B, Cuevas C:
 -asymptotically
-asymptotically  -periodic and asymptotically
-periodic and asymptotically  -periodic solutions to semi-linear Cauchy problems with non-dense domain. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):3190-3208. 10.1016/j.na.2009.12.016
-periodic solutions to semi-linear Cauchy problems with non-dense domain. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):3190-3208. 10.1016/j.na.2009.12.016Nicola SHJ, Pierri M:A note on
 -asymptotically periodic functions. Nonlinear Analysis: Real World Applications 2009,10(5):2937-2938. 10.1016/j.nonrwa.2008.09.011
-asymptotically periodic functions. Nonlinear Analysis: Real World Applications 2009,10(5):2937-2938. 10.1016/j.nonrwa.2008.09.011Pierri M:On
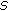 -asymptotically
-asymptotically  -periodic functions and applications. submitted
-periodic functions and applications. submittedCuesta E: Asymptotic behaviour of the solutions of fractional integro-differential equations and some time discretizations. Discrete and Continuous Dynamical Systems. Series A 2007, 2007: 277-285.
Anh VV, Mcvinish R: Fractional differential equations driven by Lévy noise. Journal of Applied Mathematics and Stochastic Analysis 2003,16(2):97-119. 10.1155/S1048953303000078
Gorenflo R, Mainardi F: Fractional calculus: integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics (Udine, 1996), CISM Courses and Lectures. Volume 378. Edited by: Carpinteri A, Mainardi F. Springer, Vienna, Austria; 1997:223-276.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Nigmatullin RR, Trujillo JJ: Mesoscopic fractional kinetic equations versus a Riemann-Liouville integral type. In Advances in Fractional Calculus. Springer, Dordrecht, The Netherlands; 2007:155-167.
Rivero M, Trujillo JJ, Velasco MP: On deterministic fractional models. In New Trends in Nanotechnology and Fractional Calculus Applications. Springer, New York, NY, USA; 2010:123-150.
Agarwal RP, de Andrade B, Cuevas C: Weighted pseudo-almost periodic solutions of a class of semilinear fractional differential equations. Nonlinear Analysis: Real World Applications 2010, 11: 3532-3554. 10.1016/j.nonrwa.2010.01.002
Agarwal RP, de Andrade B, Cuevas C: On type of periodicity and ergodicity to a class of fractional order differential equations. Advances in Difference Equations 2010, 2010:-25.
Agarwal RP, Belmekki M, Benchohra M: A survey on semilinear differential equations and inclusions involving Riemann-Liouville fractional derivative. Advances in Difference Equations 2009, 2009:-47.
Agarwal RP, Benchohra M, Hamani S: A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions. Acta Applicandae Mathematicae 2010,109(3):973-1033. 10.1007/s10440-008-9356-6
Agarwal RP, Lakshmikantham V, Nieto JJ: On the concept of solution for fractional differential equations with uncertainty. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):2859-2862. 10.1016/j.na.2009.11.029
Agarwal RP, Zhou Y, He Y: Existence of fractional neutral functional differential equations. Computers & Mathematics with Applications 2010,59(3):1095-1100.
Agarwal RP, Cuevas C, Soto H, El-Gebeily M: Asymptotic periodicity for some evolution equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications. In press
Cuesta E, Lubich C, Palencia C: Convolution quadrature time discretization of fractional diffusion-wave equations. Mathematics of Computation 2006,75(254):673-696. 10.1090/S0025-5718-06-01788-1
dos Santos JPC, Cuevas C: Asymptotically almost automorphic solutions of abstract fractional integro-differential neutral equations. Applied Mathematics Letters 2010,23(9):960-965. 10.1016/j.aml.2010.04.016
Eidelman SD, Kochubei AN: Cauchy problem for fractional diffusion equations. Journal of Differential Equations 2004,199(2):211-255. 10.1016/j.jde.2003.12.002
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Devi JV: Theory of fractional differential equations in a Banach space. European Journal of Pure and Applied Mathematics 2008,1(1):38-45.
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Lakshmikantham V, Vatsala AS: Theory of fractional differential inequalities and applications. Communications in Applied Analysis 2007,11(3-4):395-402.
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
N'Guérékata GM: A Cauchy problem for some fractional abstract differential equation with non local conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1873-1876. 10.1016/j.na.2008.02.087
Hilfe R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Keyantuo V, Lizama C: On a connection between powers of operators and fractional Cauchy problems. submitted
Acknowledgments
C. Cuevas thanks the Department of Mathematics of Universidad de La Frontera, where this project was started. The authors are grateful to the referees for their valuable comments and suggestions. C. Cuevas is partially supported by CNPQ/Brazil under Grant 300365/2008-0.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cuevas, C., Pierri, M. & Sepulveda, A. Weighted 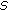 -Asymptotically
-Asymptotically  -Periodic Solutions of a Class of Fractional Differential Equations.
Adv Differ Equ 2011, 584874 (2011). https://doi.org/10.1155/2011/584874
-Periodic Solutions of a Class of Fractional Differential Equations.
Adv Differ Equ 2011, 584874 (2011). https://doi.org/10.1155/2011/584874
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/584874
 -Asymptotically
-Asymptotically  -Periodic Functions
-Periodic Functions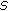 -Asymptotically
-Asymptotically  -Periodic Solutions
-Periodic Solutions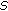 -asymptotically
-asymptotically  -periodic functions on Banach spaces and applications. Journal of Mathematical Analysis and Applications 2008,343(2):1119-1130. 10.1016/j.jmaa.2008.02.023
-periodic functions on Banach spaces and applications. Journal of Mathematical Analysis and Applications 2008,343(2):1119-1130. 10.1016/j.jmaa.2008.02.023 -asymptotically
-asymptotically  -periodic solutions for abstract neutral equations. Bulletin of the Australian Mathematical Society 2008,78(3):365-382. 10.1017/S0004972708000713
-periodic solutions for abstract neutral equations. Bulletin of the Australian Mathematical Society 2008,78(3):365-382. 10.1017/S0004972708000713 -asymptotically
-asymptotically  -periodic solutions of abstract partial neutral integro-differentail equations. Functional Differential Equations 2010,17(1-2):387-405.
-periodic solutions of abstract partial neutral integro-differentail equations. Functional Differential Equations 2010,17(1-2):387-405. -asymptotically
-asymptotically  -periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013
-periodic solutions of semilinear fractional integro-differential equations. Applied Mathematics Letters 2009,22(6):865-870. 10.1016/j.aml.2008.07.013 -asymptotically
-asymptotically  -periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007
-periodic solutions for fractional order functional integro-differential equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1683-1689. 10.1016/j.na.2009.09.007 -asymptotically
-asymptotically  -periodic solutions for semilinear Volterra equations. Mathematical Methods in the Applied Sciences 2010,33(13):1628-1636.
-periodic solutions for semilinear Volterra equations. Mathematical Methods in the Applied Sciences 2010,33(13):1628-1636. -asymptotically
-asymptotically  -periodic and asymptotically
-periodic and asymptotically  -periodic solutions to semi-linear Cauchy problems with non-dense domain. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):3190-3208. 10.1016/j.na.2009.12.016
-periodic solutions to semi-linear Cauchy problems with non-dense domain. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):3190-3208. 10.1016/j.na.2009.12.016 -asymptotically periodic functions. Nonlinear Analysis: Real World Applications 2009,10(5):2937-2938. 10.1016/j.nonrwa.2008.09.011
-asymptotically periodic functions. Nonlinear Analysis: Real World Applications 2009,10(5):2937-2938. 10.1016/j.nonrwa.2008.09.011 -asymptotically
-asymptotically  -periodic functions and applications. submitted
-periodic functions and applications. submitted