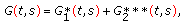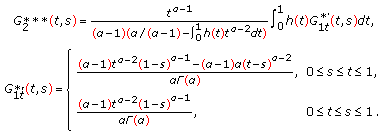- Research Article
- Open access
- Published:
The Existence of Positive Solution to a Nonlinear Fractional Differential Equation with Integral Boundary Conditions
Advances in Difference Equations volume 2011, Article number: 546038 (2011)
Abstract
The expression and properties of Green's function for a class of nonlinear fractional differential equations with integral boundary conditions are studied and employed to obtain some results on the existence of positive solutions by using fixed point theorem in cones. The proofs are based on the reduction of the problem considered to the equivalent Fredholm integral equation of the second kind. The results significantly extend and improve many known results even for integer-order cases.
1. Introduction
Fractional calculus is an area having a long history, its infancy dates back to three hundred years, the beginnings of classical calculus. It had attracted the interest of many old famous mathematicians, such as L'Hospital, Leibniz, Liouville, Riemann, Grünward, Letnikov, and so forth [1, 2]. As the old mathematicians expected, in recent several decades fractional differential equations have been found to be a powerful tool in more and more fields, such as materials, physics, mechanics, and engineering [1–5]. For the basic theory and recent development of the subject, we refer the reader to a text by Lakshmikantham et al. [6]. For more details and examples, see [7–24] and the references therein. However, the theory of boundary value problems for nonlinear fractional differential equations is still in the initial stages, and many aspects of this theory need to be explored.
In [13], Bai and Lü used the fixed point theorems to show the existence and multiplicity of positive solutions to the nonlinear fractional boundary value problem

where  ,
,  is the standard Riemann-Liouville differentiation, and
is the standard Riemann-Liouville differentiation, and  is a given continuous function.
is a given continuous function.
In [15], Zhang showed the existence and multiplicity of positive solutions of the fractional boundary value problem

where  is a real number, and
is a real number, and  is the Caputo's fractional derivative. The function
is the Caputo's fractional derivative. The function  is continuous on
is continuous on  .
.
Recently, Ahmad and Nieto [11] investigated some existence results for a nonlinear fractional integrodifferential equation with integral boundary conditions

where  is the Caputo fractional derivative,
is the Caputo fractional derivative,  , for
, for  ,
,

 ,
,  ,
,  are real numbers, and
are real numbers, and  is a Banach space.
is a Banach space.
Being directly inspired by [11, 13, 15], we intend in this paper to study the following boundary value problems of fractional order differential equation

where  ,
,  and
and  may be singular at
may be singular at  or/and at
or/and at  is the standard Riemann-Liouville differentiation,
is the standard Riemann-Liouville differentiation,  is nonnegative, and
is nonnegative, and  .
.
In the case of  , for all
, for all  , boundary value problem (1.5) reduces to the problem studied by Kaufmann and Mboumi [19]. In [19], the authors used the fixed point theorems to show sufficient conditions for the existence of at least one and at least three positive solutions to problem (1.5). For the case of
, boundary value problem (1.5) reduces to the problem studied by Kaufmann and Mboumi [19]. In [19], the authors used the fixed point theorems to show sufficient conditions for the existence of at least one and at least three positive solutions to problem (1.5). For the case of  , boundary value problem (1.5) is related to a boundary value problems of integer-order differential equation. Feng et al. [25] considered the existence and multiplicity of positive solutions to boundary value problem (1.5) by applying the fixed point theory in a cone for strict set contraction operators.
, boundary value problem (1.5) is related to a boundary value problems of integer-order differential equation. Feng et al. [25] considered the existence and multiplicity of positive solutions to boundary value problem (1.5) by applying the fixed point theory in a cone for strict set contraction operators.
The organization of this paper is as follows. We will introduce some lemmas and notations in the rest of this section. In Section 2, we present the expression and properties of Green's function associated with boundary value problem (1.5). In Section 3, we give some preliminaries about operator. In particular, we state fixed point theory in cones. In Section 4, the main results of boundary value problem (1.5) will be stated and proved. In Section 5, we offer some interesting discussion of the associated boundary value problem (1.5). Finally, conclusions in Section 6 close the paper.
The fractional differential equations-related notations adopted in this paper can be found, if not explained specifically, in almost all literature related to fractional differential equations. The readers who are unfamiliar with this area can consult for example [1–6] for details.
Definition 1.1 (see [4]).
The integral

where  is called Riemann-Liouville fractional integral of order
is called Riemann-Liouville fractional integral of order  .
.
Definition 1.2 (see [4]).
For a function  given in the interval
given in the interval  , the expression
, the expression

where  ,
,  denotes the integer part of number
denotes the integer part of number  , is called the Riemann-Liouville fractional derivative of order
, is called the Riemann-Liouville fractional derivative of order  .
.
Lemma 1.3 (see [13]).
Assume that  with a fractional derivative of order
with a fractional derivative of order  that belongs to
that belongs to  . Then
. Then

for some  ,
,  , where
, where  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to  .
.
2. Expression and Properties of Green's Function
In this section, we present the expression and properties of Green's function associated with boundary value problem (1.5).
Lemma 2.1.
Assume that  . Then for any
. Then for any  , the unique solution of boundary value problem
, the unique solution of boundary value problem

is given by

where



Proof.
By Lemma 1.3, we can reduce the equation of problem (2.1) to an equivalent integral equation

By  , there is
, there is  , and
, and

By (2.7) and  , we have
, we have

which yields that

Therefore, the unique solution of BVP (2.1) is

where  is defined by (2.4).
is defined by (2.4).
Multiplying (2.10) with  and integrating it, we can see
and integrating it, we can see

Therefore,

Substituting (2.12) into (2.10), we obtain

where  ,
,  , and
, and  are defined by (2.3), (2.4), and (2.5), respectively. The proof is complete.
are defined by (2.3), (2.4), and (2.5), respectively. The proof is complete.
From (2.3), (2.4), and (2.5), we can prove that  , and
, and  have the following properties.
have the following properties.
Proposition 2.2.
The function  defined by (2.4) satisfies the following.
defined by (2.4) satisfies the following.
-
(i)
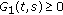 is continuous for all
is continuous for all  ,
,  , for all
, for all  ;
; -
(ii)
 , for all
, for all 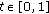 ,
,  .
.
Proof.
-
(i)
It is obvious that
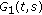 is continuous on
is continuous on 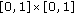 . For
. For 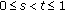 ,
,  (214)
(214)
So, by (2.4), we have

Similarly, for  , we have
, we have  .
.
-
(ii)
Since
 , for given
, for given  ,
, 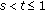 , we have
, we have  (216)
(216)

Therefore, from (2.17) and the definition of  , for given
, for given  ,
,  , we have
, we have

On the other hand, it is clear that

Therefore, we have

Let

Proposition 2.3.
If  , then one has
, then one has
-
(i)
 is continuous for all
is continuous for all  ,
,  , for all
, for all 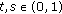 ;
; -
(ii)
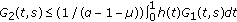 , for all
, for all 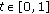 ,
, 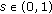 .
.
Proof.
From the properties of  , and the definition of
, and the definition of  , we can prove that the results of Proposition 2.3 hold.
, we can prove that the results of Proposition 2.3 hold.
Theorem 2.4.
If  , the function
, the function  defined by (2.3) satisfies the following.
defined by (2.3) satisfies the following.
-
(i)
 is continuous for all
is continuous for all 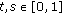 ,
,  , for all
, for all 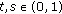 ;
; -
(ii)
(
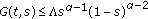 , for all
, for all 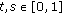 , where
, where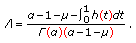 (222)
(222)
Proof.
-
(i)
From Propositions 2.2 and 2.3, we obtain that
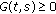 is continuous for all
is continuous for all 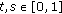 ,
, 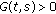 , for all
, for all  .
. -
(ii)
From Proposition 2.2 and (2.3), we have
 (223)
(223)
Remark 2.5.
From (i) of Theorem 2.4, we obtain that there exists  such that
such that

where  .
.
3. Preliminaries
In this section, we give some preliminaries for discussing the existence of positive solutions of boundary value problem (1.5).
Let  . The basic space used in this paper is
. The basic space used in this paper is  . It is well known that
. It is well known that  is a real Banach space with the norm
is a real Banach space with the norm  defined by
defined by  . Let
. Let

where  .
.
On the basis of Lemma 3.3 below we will establish in Section 4 the existence of positive solution to the problem (1.5). Here we make the following hypotheses:
(H
1
) ,
,  on any subinterval of (0,1) and
on any subinterval of (0,1) and  ;
;
(H
2
) and
and  uniformly with respect to
uniformly with respect to  on
on  ;
;
(H
3
) , where
, where  is defined by (2.21).
is defined by (2.21).
Define  by
by

where  is defined by (2.3).
is defined by (2.3).
Lemma 3.1.
Let (H1)–(H3) hold. Then boundary value problems (1.5) has a solution  if and only if
if and only if  is a fixed point of
is a fixed point of  .
.
Proof.
From Lemma 2.1, we can prove the results of this Lemma.
Lemma 3.2.
Let (H1)–(H3) hold. Then  and
and  is completely continuous.
is completely continuous.
Proof.
For any  , by (3.2), we can obtain
, by (3.2), we can obtain  . Next by similar proof of Lemma 3.1 in [12] and Ascoli-Arzela theorem one can prove
. Next by similar proof of Lemma 3.1 in [12] and Ascoli-Arzela theorem one can prove  is completely continuous. So it is omitted.
is completely continuous. So it is omitted.
Lemma 3.3 (see [26]).
Let  and
and  be two bounded open sets in a real Banach space
be two bounded open sets in a real Banach space  , such that
, such that  and
and  . Let operator
. Let operator  be completely continuous, where
be completely continuous, where  is a cone in
is a cone in  . Suppose that one of the following two conditions is satisfied.
. Suppose that one of the following two conditions is satisfied.
-
(i)
There exists
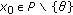 such that
such that  , for all
, for all  ,
, ;
; 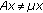 , for all
, for all 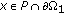 ,
, 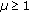 .
. -
(ii)
There exists
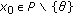 such that
such that 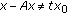 , for all
, for all  ,
,  ;
;  , for all
, for all 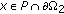 ,
,  .
.
Then,  has at least one fixed point in
has at least one fixed point in  .
.
4. Existence of Positive Solutions
In this section, we apply Lemma 3.3 to establish the existence of positive solutions for boundary value problems (1.5).
Theorem 4.1.
Suppose (H1)– (H3) and  satisfies the following conditions.
satisfies the following conditions.
(H4)There exists  such that
such that  ;
;
(H5)There exists  such that
such that  .
.
Then boundary value problems (1.5) has at least one positive solution.
Proof.
For applying Lemma 3.3, we construct a function  via
via

Obviously,  is a nonnegative continuous function, that is,
is a nonnegative continuous function, that is,  , and
, and  .
.
Suppose that there is  such that
such that

if not, then the conclusion holds. The condition (H
4
) and  imply that there exist
imply that there exist  ,
,  such that
such that

Let  , and choose
, and choose  . We now show that
. We now show that

In fact, if there exist  ,
,  such that
such that  , then (4.4) implies that
, then (4.4) implies that  . On the other hand,
. On the other hand,  . So we can choose
. So we can choose  , then
, then  ,
,  . Therefore,
. Therefore,

Consequently, for any  , (2.24) and (4.3) imply
, (2.24) and (4.3) imply

that is,  ,
,  . Noticing the definition of
. Noticing the definition of  , we have
, we have

which is a contradiction to the definition of  . Hence, (4.4) holds.
. Hence, (4.4) holds.
Now turning to (H
5
), there exist  ,
,  , for
, for  ,
,  , such that
, such that  . Letting
. Letting  , then
, then

Choosing  such that
such that

where  . Now we prove that
. Now we prove that

If not, then there exist  such that
such that  . By (4.8) and (ii) of Theorem 2.4, then for any
. By (4.8) and (ii) of Theorem 2.4, then for any  , we have
, we have

So  , that is,
, that is,

which is a contradiction to (4.9). So, (4.10) holds.
By (ii) of Lemma 3.3, (4.4) and (4.10) yield that  has a fixed point
has a fixed point  ,
,  . Thus it follows that boundary value problems (1.5) has at least one positive solution
. Thus it follows that boundary value problems (1.5) has at least one positive solution  with
with  . The proof is complete.
. The proof is complete.
5. Discussion
In this section, we offer some interesting discussion associated with boundary value problems (1.5).
Since the proof of the main theorem (Theorem 4.1) in this paper is independent of the expression form of  and only dependent on its continuity and nonnegativity, there are similar conclusions by analogous methods for boundary value problems (1.5) subject to other boundary value conditions, respectively, the following.
and only dependent on its continuity and nonnegativity, there are similar conclusions by analogous methods for boundary value problems (1.5) subject to other boundary value conditions, respectively, the following.
-
(i)
We have
 (51)
(51)then
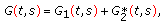 (52)
(52)where
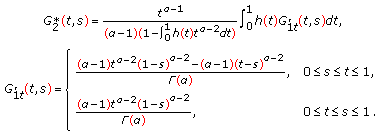 (53)
(53)Obviously
 is continuous on
is continuous on  , and it is easy to see that
, and it is easy to see that  by
by  , where
, where (54)
(54) -
(ii)
We have
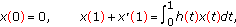 (55)
(55)then
 (56)
(56)where
 (57)
(57)Obviously
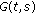 is continuous on
is continuous on 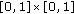 , and it is easy to see that
, and it is easy to see that 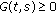 ,
, 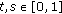 by
by  , where
, where 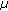 is defined by (2.21).
is defined by (2.21). -
(iii)
We have
 (58)
(58)then
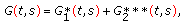 (59)
(59)where
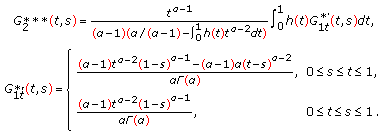 (510)
(510)
Obviously  is continuous on
is continuous on  , and it is easy to see that
, and it is easy to see that  by
by  , where
, where  is defined in (5.4).
is defined in (5.4).
6. Conclusions
In this paper, by using the fixed point theorem of cone, we have investigated the existence of positive solutions for a class of nonlinear fractional differential equations with integral boundary conditions and have obtained some easily verifiable sufficient criteria which extend previous results. It is worth mentioning that there are still many problems that remain open in this vital field other than the results obtained in this paper: for example, whether or not we can study the fractional differential equations with integral boundary conditions at resonance (see, e.g., [27]), and whether or not we can give a unified approach applicable to many BVPs (see, e.g., [28–31]). More efforts are still needed in the future.
References
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, London, UK; 1974:xiii+234.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Gordon and Breach Science Publishers, Yverdon, Switzerland; 1993:xxxvi+976.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science, Amsterdam, The Netherlands; 2006:xvi+523.
Lakshmikantham V, Leela S, Vasundhara Devi J: Theory of Fractional Dynamic Systems. Cambridge Academic, Cambridge, UK; 2009.
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis. Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Daftardar-Gejji V: Positive solutions of a system of non-autonomous fractional differential equations. Journal of Mathematical Analysis and Applications 2005,302(1):56-64. 10.1016/j.jmaa.2004.08.007
Daftardar-Gejji V, Bhalekar S: Boundary value problems for multi-term fractional differential equations. Journal of Mathematical Analysis and Applications 2008,345(2):754-765. 10.1016/j.jmaa.2008.04.065
Ahmad B, Nieto JJ: Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions. Nonlinear Analysis. Theory, Methods & Applications 2008,69(10):3291-3298. 10.1016/j.na.2007.09.018
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
Bai Z: On positive solutions of a nonlocal fractional boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2010,72(2):916-924. 10.1016/j.na.2009.07.033
Bai Z, Lü H: Positive solutions for boundary value problem of nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2005,311(2):495-505. 10.1016/j.jmaa.2005.02.052
Jiang D, Yuan C: The positive properties of the Green function for Dirichlet-type boundary value problems of nonlinear fractional differential equations and its application. Nonlinear Analysis. Theory, Methods & Applications 2010,72(2):710-719. 10.1016/j.na.2009.07.012
Zhang S: Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electronic Journal of Differential Equations 2006, (36):1-12.
Benchohra M, Hamani S, Ntouyas SK: Boundary value problems for differential equations with fractional order and nonlocal conditions. Nonlinear Analysis. Theory, Methods & Applications 2009,71(7-8):2391-2396. 10.1016/j.na.2009.01.073
Salem HAH: On the nonlinear Hammerstein integral equations in Banach spaces and application to the boundary value problem of fractional order. Mathematical and Computer Modelling 2008,48(7-8):1178-1190. 10.1016/j.mcm.2007.12.015
Salem HAH: On the fractional order m-point boundary value problem in reflexive Banach spaces and weak topologies. Journal of Computational and Applied Mathematics 2009,224(2):565-572. 10.1016/j.cam.2008.05.033
Kaufmann ER, Mboumi E: Positive solutions of a boundary value problem for a nonlinear fractional differential equation. Electronic Journal of Qualitative Theory of Differential Equations 2008, (3):1-11.
Li CF, Luo XN, Zhou Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Computers & Mathematics with Applications 2010,59(3):1363-1375.
Zhang S: The existence of a positive solution for a nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2000,252(2):804-812. 10.1006/jmaa.2000.7123
Zhang S: Existence of positive solution for some class of nonlinear fractional differential equations. Journal of Mathematical Analysis and Applications 2003,278(1):136-148. 10.1016/S0022-247X(02)00583-8
Zhong W, Lin W: Nonlocal and multiple-point boundary value problem for fractional differential equations. Computers & Mathematics with Applications 2010,59(3):1345-1351.
Feng M, Zhang X, Ge W: New existence results for higher-order nonlinear fractional differential equation with integral boundary conditions. Boundary Value Problems 2011, 2011:-20.
Feng M, Ji D, Ge W: Positive solutions for a class of boundary-value problem with integral boundary conditions in Banach spaces. Journal of Computational and Applied Mathematics 2008,222(2):351-363. 10.1016/j.cam.2007.11.003
Guo D, Lakshmikantham V, Liu X: Nonlinear Integral Equations in Abstract Spaces, Mathematics and Its Applications. Volume 373. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:viii+341.
Zhang X, Feng M, Ge W: Existence result of second-order differential equations with integral boundary conditions at resonance. Journal of Mathematical Analysis and Applications 2009,353(1):311-319. 10.1016/j.jmaa.2008.11.082
Infante G, Webb JRL: Nonlinear non-local boundary-value problems and perturbed Hammerstein integral equations. Proceedings of the Edinburgh Mathematical Society. Series II 2006,49(3):637-656. 10.1017/S0013091505000532
Webb JRL: Positive solutions of some three point boundary value problems via fixed point index theory. Nonlinear Analysis. Theory, Methods & Applications 2001,47(7):4319-4332. 10.1016/S0362-546X(01)00547-8
Webb JRL, Infante G: Positive solutions of nonlocal boundary value problems: a unified approach. Journal of the London Mathematical Society. Second Series 2006,74(3):673-693. 10.1112/S0024610706023179
Webb JRL, Infante G, Franco D: Positive solutions of nonlinear fourth-order boundary-value problems with local and non-local boundary conditions. Proceedings of the Royal Society of Edinburgh. Section A 2008,138(2):427-446.
Acknowledgments
The authors thank the referee for his/her careful reading of the paper and useful suggestions. This paper is sponsored by the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the jurisdiction of Beijing Municipality (PHR201008430), the Scientific Research Common Program of Beijing Municipal Commission of Education (KM201010772018), the Natural Sciences Foundation of Heibei Province (A2009001426), and the Beijing Excellent Training Grant (2010D005007000002).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feng, M., Liu, X. & Feng, H. The Existence of Positive Solution to a Nonlinear Fractional Differential Equation with Integral Boundary Conditions. Adv Differ Equ 2011, 546038 (2011). https://doi.org/10.1155/2011/546038
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/546038
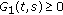 is continuous for all
is continuous for all  ,
,  , for all
, for all  ;
; , for all
, for all 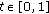 ,
,  .
.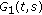 is continuous on
is continuous on 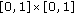 . For
. For 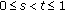 ,
, 
 , for given
, for given  ,
, 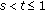 , we have
, we have 
 is continuous for all
is continuous for all  ,
,  , for all
, for all 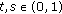 ;
;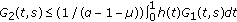 , for all
, for all 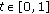 ,
, 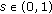 .
. is continuous for all
is continuous for all 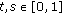 ,
,  , for all
, for all 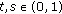 ;
;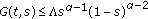 , for all
, for all 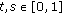 , where
, where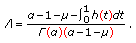
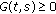 is continuous for all
is continuous for all 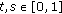 ,
, 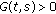 , for all
, for all  .
.
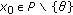 such that
such that  , for all
, for all  ,
, ;
; 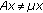 , for all
, for all 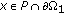 ,
, 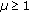 .
.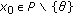 such that
such that 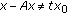 , for all
, for all  ,
,  ;
;  , for all
, for all 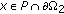 ,
,  .
.
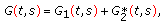
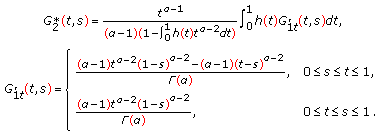
 is continuous on
is continuous on  , and it is easy to see that
, and it is easy to see that  by
by  , where
, where
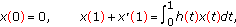


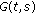 is continuous on
is continuous on 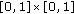 , and it is easy to see that
, and it is easy to see that 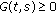 ,
, 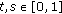 by
by  , where
, where 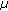 is defined by (2.21).
is defined by (2.21).