- Research Article
- Open access
- Published:
Existence and Uniqueness of Positive Solutions for Discrete Fourth-Order Lidstone Problem with a Parameter
Advances in Difference Equations volume 2010, Article number: 971540 (2010)
Abstract
This work presents sufficient conditions for the existence and uniqueness of positive solutions for a discrete fourth-order beam equation under Lidstone boundary conditions with a parameter; the iterative sequences yielding approximate solutions are also given. The main tool used is monotone iterative technique.
1. Introduction
In this paper, we are interested in the existence, uniqueness, and iteration of positive solutions for the following nonlinear discrete fourth-order beam equation under Lidstone boundary conditions with explicit parameter  given by
given by


where  is the usual forward difference operator given by
is the usual forward difference operator given by  ,
,  ,
,  , and
, and  is a real parameter.
is a real parameter.
In recent years, the theory of nonlinear difference equations has been widely applied to many fields such as economics, neural network, ecology, and cybernetics, for details, see [1–7] and references therein. Especially, there was much attention focused on the existence and multiplicity of positive solutions of fourth-order problem, for example, [8–10], and in particular the discrete problem with Lidstone boundary conditions [11–17]. However, very little work has been done on the uniqueness and iteration of positive solutions of discrete fourth-order equation under Lidstone boundary conditions. We would like to mention some results of Anderson and Minhós [11] and He and Su [12], which motivated us to consider the BVP (1.1) and (1.2).
In [11], Anderson and Minhós studied the following nonlinear discrete fourth-order equation with explicit parameters  and
and  given by
given by

with Lidstone boundary conditions (1.2), where  and
and  are real parameters. The authors obtained the following result.
are real parameters. The authors obtained the following result.
Theorem 1.1 (see [11]).
Assume that the following condition is satisfied
 , where
, where  with
with  ,
,  is continuous and nondecreasing, and there exists
is continuous and nondecreasing, and there exists  such that
such that  for
for  and
and 
then, for any  , the BVP (1.3) and (1.2) has a unique positive solution
, the BVP (1.3) and (1.2) has a unique positive solution  . Furthermore, such a solution
. Furthermore, such a solution  satisfies the following properties:
satisfies the following properties:
-
(i)
 and
and  ;
; -
(ii)
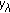 is nondecreasing in
is nondecreasing in 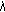 ;
; -
(iii)
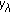 is continuous in
is continuous in 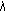 , that is, if
, that is, if  , then
, then  .
.
Very recently, in [12], He and Su investigated the existence, multiplicity, and nonexistence of nontrivial solutions to the following discrete nonlinear fourth-order boundary value problem

where  denotes the forward difference operator defined by
denotes the forward difference operator defined by  ,
,  ,
,  is the discrete interval given by
is the discrete interval given by  with
with  and
and  (
( ) integers,
) integers,  are real parameters and satisfy
are real parameters and satisfy

For the function  , the authors imposed the following assumption:
, the authors imposed the following assumption:
(B1) , where
, where  with
with  ,
,  is continuous and nondecreasing, and there exists
is continuous and nondecreasing, and there exists  such that
such that  for
for  and
and  .
.
Their main result is the following theorem.
Theorem 1.2 (see [12]).
Assume that  holds. Then for any
holds. Then for any  , the BVP (1.4) has a unique positive solution
, the BVP (1.4) has a unique positive solution  . Furthermore, such a solution
. Furthermore, such a solution  satisfies the properties (i)–(iii) stated in Theorem 1.1.
satisfies the properties (i)–(iii) stated in Theorem 1.1.
The aim of this work is to relax the assumptions  and
and  on the nonlinear term, without demanding the existence of upper and lower solutions, we present conditions for the BVP (1.1) and (1.2) to have a unique solution and then study the convergence of the iterative sequence. The ideas come from Zhai et al. [18, 19] and Liang [20].
on the nonlinear term, without demanding the existence of upper and lower solutions, we present conditions for the BVP (1.1) and (1.2) to have a unique solution and then study the convergence of the iterative sequence. The ideas come from Zhai et al. [18, 19] and Liang [20].
Let  denote the Banach space of real-valued functions on
denote the Banach space of real-valued functions on  , with the supremum norm
, with the supremum norm

Throughout this paper, we need the following hypotheses:
(H1) are continuous and
are continuous and  for
for  (
( );
);
(H2) with
with  ;
;
(H3) is nondecreasing,
is nondecreasing,  is nonincreasing, and there exist
is nonincreasing, and there exist  on interval
on interval  with
with  , for all
, for all , there exists
, there exists  such that
such that  , and
, and  for all
for all  which satisfy
which satisfy

2. Two Lemmas
To prove the main results in this paper, we will employ two lemmas. These lemmas are based on the linear discrete fourth-order equation

with Lidstone boundary conditions (1.2).
Lemma 2.1 (see [11]).
Let  be a function. Then the nonhomogeneous discrete fourth-order Lidstone boundary value problem (2.1), (1.2) has solution
be a function. Then the nonhomogeneous discrete fourth-order Lidstone boundary value problem (2.1), (1.2) has solution

where  given by
given by

with  for
for  , is the Green's function for the second-order discrete boundary value problem
, is the Green's function for the second-order discrete boundary value problem

and  given by
given by

is the Green's function for the second-order discrete boundary value problem

Lemma 2.2 (see [11]).
Let

Then, for  , one has
, one has

3. Main Results
Theorem 3.1.
Assume that  hold. Then, the BVP (1.1) and (1.2) has a unique solution
hold. Then, the BVP (1.1) and (1.2) has a unique solution  in
in  , where
, where

Moreover, for any  , constructing successively the sequences
, constructing successively the sequences

One has  converge uniformly to
converge uniformly to  in
in  .
.
Proof.
First, we show that the BVP (1.1) and (1.2) has a solution.
It is easy to see that the BVP (1.1) and (1.2) has a solution  if and only if
if and only if  is a fixed point of the operator equation
is a fixed point of the operator equation

In view of  and (3.3),
and (3.3),  is nondecreasing in
is nondecreasing in  and nonincreasing in
and nonincreasing in  . Moreover, for any
. Moreover, for any  , we have
, we have

for  and
and  .
.
Let

condition  implies
implies  . Since
. Since  for
for  (
( ), by Lemma 2.2, we have
), by Lemma 2.2, we have

for  in (2.1) and
in (2.1) and  in (3.5).
in (3.5).
Moreover, we obtain

for  in (2.1).
in (2.1).
Thus

Therefore, we can choose a sufficiently small number  such that
such that

which together with  implies that there exists
implies that there exists  such that
such that  , so
, so

Since  , we can take a sufficiently large positive integer
, we can take a sufficiently large positive integer  such that
such that

It is clear that

We define

Evidently, for  ,
,  . Take any
. Take any  , then
, then  and
and  .
.
By the mixed monotonicity of  , we have
, we have  . In addition, combining
. In addition, combining  with (3.10) and (3.11), we get
with (3.10) and (3.11), we get

From  , we have
, we have

and hence

Thus, we have

In accordance with (3.12), we can see that

Construct successively the sequences

By the mixed monotonicity of  , we have
, we have  . By induction, we obtain
. By induction, we obtain  . It follows from (3.14), (3.18), and the mixed monotonicity of
. It follows from (3.14), (3.18), and the mixed monotonicity of  that
that

Note that  , so we can get
, so we can get  . Let
. Let

Thus, we have

and then

Therefore,  that is,
that is,  is increasing with
is increasing with  . Set
. Set  . We can show that
. We can show that  . In fact, if
. In fact, if  , by
, by  , there exists
, there exists  such that
such that  . Consider the following two cases.
. Consider the following two cases.
-
(i)
There exists an integer
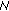 such that
such that 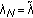 . In this case, we have
. In this case, we have 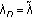 for all
for all 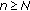 holds. Hence, for
holds. Hence, for  , it follows from (3.4) and the mixed monotonicity of
, it follows from (3.4) and the mixed monotonicity of  that
that 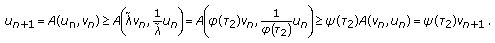 (3.24)
(3.24)By the definition of
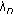 , we have
, we have (3.25)
(3.25)This is a contradiction.
-
(ii)
For all integer
 ,
,  . In this case, we have
. In this case, we have 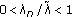 . In accordance with
. In accordance with 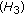 , there exists
, there exists  such that
such that  . Hence, combining (3.4) with the mixed monotonicity of
. Hence, combining (3.4) with the mixed monotonicity of 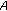 , we have
, we have  (3.26)
(3.26)
By the definition of  , we have
, we have

Let  , we have
, we have  and this is also a contradiction. Hence,
and this is also a contradiction. Hence,  .
.
Thus, combining (3.20) with (3.22), we have

for  , where
, where  is a nonnegative integer. Thus,
is a nonnegative integer. Thus,

Therefore, there exists a function  such that
such that

By the mixed monotonicity of  and (3.20), we have
and (3.20), we have

Let  and we get
and we get  ,
,  . That is,
. That is,  is a nontrivial solution of the BVP (1.1) and (1.2).
is a nontrivial solution of the BVP (1.1) and (1.2).
Next, we show the uniqueness of solutions of the BVP (1.1) and (1.2). Assume, to the contrary, that there exist two nontrivial solutions  and
and  of the BVP (1.1) and (1.2) such that
of the BVP (1.1) and (1.2) such that  and
and  for
for  . According to (3.9), we can know that there exists
. According to (3.9), we can know that there exists  such that
such that  for
for  . Let
. Let

Then  and
and  for
for  .
.
We now show that  . In fact, if
. In fact, if  , then, in view of
, then, in view of  , there exists
, there exists  such that
such that  . Furthermore, we have
. Furthermore, we have


In (3.34), we used the relation formula (3.16). Since  , this contradicts the definition of
, this contradicts the definition of  . Hence
. Hence  . Therefore, the BVP (1.1) and (1.2) has a unique solution.
. Therefore, the BVP (1.1) and (1.2) has a unique solution.
Finally, we show that "moreover part of the theorem. For any initial
part of the theorem. For any initial  , in accordance with (3.9), we can choose a sufficiently small number
, in accordance with (3.9), we can choose a sufficiently small number  such that
such that

It follows from  that there exists
that there exists  such that
such that  , and hence
, and hence

Thus, we can choose a sufficiently large positive integer  such that
such that

Define

Obviously,  . Let
. Let

for  . By induction, we get
. By induction, we get  ,
,  ,
,  .
.
Similarly to the above proof, it follows that there exists  such that
such that

By the uniqueness of fixed points  in
in  , we get
, we get  . Therefore, we have
. Therefore, we have

This completes the proof of the theorem.
Remark 3.2.
From the proof of Theorem 3.1, we easily know that assume  ,
,  , thus, let
, thus, let  ,
,  , we have
, we have

Therefore  .
.
Theorem 3.3.
Assume that  holds, and the following conditions are satisfied:
holds, and the following conditions are satisfied:
 is continuous and
is continuous and  for
for  ;
;
 is nondecreasing;
is nondecreasing;

for all  , where
, where  , for all
, for all  , there exists
, there exists  such that
such that  , and
, and  , with
, with  for all
for all  ;
;
for fixed  , one has
, one has
-
(i)
 is nonincreasing with respect to
is nonincreasing with respect to 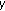 , and there exists
, and there exists  such that
such that (3.44)
(3.44)or
-
(ii)
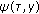 is nondecreasing with respect to
is nondecreasing with respect to  , and there exists
, and there exists 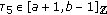 such that
such that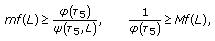 (3.45)
(3.45)where
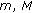 are defined in (2.1),
are defined in (2.1), 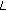 is defined in (3.5). Then, the BVP
is defined in (3.5). Then, the BVP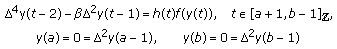 (3.46)
(3.46)has a unique solution
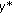 .
.
Proof.
For convenience, we still define the operator equation  by
by

In the following, we consider the following two cases.
(i) For fixed  ,
,  is nonincreasing with respect to
is nonincreasing with respect to  .
.
According to condition  and Lemma 2.2, we can know that there exists
and Lemma 2.2, we can know that there exists  such that
such that

Since  , we can find a sufficiently large positive integer
, we can find a sufficiently large positive integer  such that
such that

For  , we still define
, we still define

By the proof of Theorem 3.1, it is sufficient to show that

Obviously,  and
and  .
.
In this case, it follows from conditions  ,
,  , and (3.49) that
, and (3.49) that

In accordance with (3.16), we have

which together with condition  and (3.48) implies that
and (3.48) implies that

(ii) For fixed  ,
,  is nondecreasing with respect to
is nondecreasing with respect to  .
.
In this case, by condition  and Lemma 2.2, we can know that there exists
and Lemma 2.2, we can know that there exists  such that
such that

Since  , we can take a sufficiently large positive integer
, we can take a sufficiently large positive integer  such that
such that

For  , we still define
, we still define

We continue to prove that

By (3.52), combining (3.55) with the monotonicity of  , we have
, we have

In accordance with (3.54), combining the monotonicity of  and (3.55), we get
and (3.55), we get

An application of (3.56) yields

Therefore, we obtain

For  , the proof is similar and hence omitted. This completes the proof of the theorem.
, the proof is similar and hence omitted. This completes the proof of the theorem.
Remark 3.4.
In Theorem 3.1, the more general conditions are imposed on the nonlinear term than Theorem 1.1. In particular, in Theorem 3.3,  contains the variable
contains the variable  ; therefore, the more comprehensive functions can be incorporated.
; therefore, the more comprehensive functions can be incorporated.
4. An Example
Example 4.1.
Consider the following discrete fourth-order Lidstone problem:

We claim that the BVP (4.1) and (1.2) has a unique solution  in
in  , where
, where

Moreover, for any  , constructing successively the sequences
, constructing successively the sequences

we have  converge uniformly to
converge uniformly to  in
in  .
.
In fact, we choose  ,
,  ,
,  , thus
, thus  for
for  ,
,  . It is easy to check that
. It is easy to check that  is nondecreasing on
is nondecreasing on  ,
,  is nonincreasing on
is nonincreasing on  . In addition, we set
. In addition, we set

 . It is easy to see that
. It is easy to see that

The conclusion then follows from Theorem 3.1.
References
Agarwal RP: Difference Equations and Inequalities. Volume 155. Marcel Dekker, New York, NY, USA; 1992:xiv+777.
Agarwal RP, O'Regan D, Wong PJY: Positive Solutions of Differential, Difference and Integral Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1999:xii+417.
Agarwal RP, Perera K, O'Regan D: Multiple positive solutions of singular and nonsingular discrete problems via variational methods. Nonlinear Analysis: Theory, Methods & Applications 2004,58(1-2):69-73. 10.1016/j.na.2003.11.012
Lakshmikantham V, Trigiante D: Theory of Difference Equations: Numerical Methods and Applications. Volume 181. Academic Press, Boston, Mass, USA; 1988:x+242.
Kelley WG, Peterson AC: Difference Equations: An Introduction with Applications. Academic Press, Boston, Mass, USA; 1991:xii+455.
Yu J, Guo Z: On boundary value problems for a discrete generalized Emden-Fowler equation. Journal of Differential Equations 2006,231(1):18-31. 10.1016/j.jde.2006.08.011
Wang DB, Guan W:Three positive solutions of boundary value problems for
 -Laplacian difference equations. Computers & Mathematics with Applications 2008,55(9):1943-1949. 10.1016/j.camwa.2007.08.033
-Laplacian difference equations. Computers & Mathematics with Applications 2008,55(9):1943-1949. 10.1016/j.camwa.2007.08.033Zhang B, Kong L, Sun Y, Deng X: Existence of positive solutions for BVPs of fourth-order difference equations. Applied Mathematics and Computation 2002,131(2-3):583-591. 10.1016/S0096-3003(01)00171-0
He Z, Yu J: On the existence of positive solutions of fourth-order difference equations. Applied Mathematics and Computation 2005,161(1):139-148. 10.1016/j.amc.2003.12.016
Manojlović JV: Classification and existence of positive solutions of fourth-order nonlinear difference equations. Lithuanian Mathematical Journal 2009,49(1):71-92. 10.1007/s10986-009-9029-9
Anderson DR, Minhós F: A discrete fourth-order Lidstone problem with parameters. Applied Mathematics and Computation 2009,214(2):523-533. 10.1016/j.amc.2009.04.034
He T, Su Y: On discrete fourth-order boundary value problems with three parameters. Journal of Computational and Applied Mathematics 2010,233(10):2506-2520. 10.1016/j.cam.2009.10.032
Agarwal RP, O'Regan D: Lidstone continuous and discrete boundary value problems. Memoirs on Differential Equations and Mathematical Physics 2000, 19: 107-125.
Wong PJY, Agarwal RP: Multiple solutions of difference and partial difference equations with Lidstone conditions. Mathematical and Computer Modelling 2000,32(5-6):699-725. 10.1016/S0895-7177(00)00166-7
Wong PJY, Agarwal RP: Results and estimates on multiple solutions of Lidstone boundary value problems. Acta Mathematica Hungarica 2000,86(1-2):137-168. 10.1023/A:1006751703693
Wong PJY, Agarwal RP: Characterization of eigenvalues for difference equations subject to Lidstone conditions. Japan Journal of Industrial and Applied Mathematics 2002,19(1):1-18. 10.1007/BF03167445
Wong PJY, Xie L: Three symmetric solutions of Lidstone boundary value problems for difference and partial difference equations. Computers & Mathematics with Applications 2003,45(6–9):1445-1460. 10.1016/S0898-1221(03)00102-0
Zhai C-B, Cao X-M:Fixed point theorems for
 -
-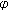 -concave operators and applications. Computers and Mathematics with Applications 2010,59(1):532-538. 10.1016/j.camwa.2009.06.016
-concave operators and applications. Computers and Mathematics with Applications 2010,59(1):532-538. 10.1016/j.camwa.2009.06.016Zhai CB, Wang WX, Zhang LL: Generalizations for a class of concave and convex operators. Acta Mathematica Sinica 2008,51(3):529-540.
Liang ZD: Existence and uniqueness of fixed points for mixed monotone operators. Journal of Dezhou University 2008,24(4):1-6.
Acknowledgments
The authors were supported financially by the National Natural Science Foundation of China (10971046), the Natural Science Foundation of Shandong Province (ZR2009AM004), and the Youth Science Foundation of Shanxi Province (2009021001-2).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sang, Y., Wei, Z. & Dong, W. Existence and Uniqueness of Positive Solutions for Discrete Fourth-Order Lidstone Problem with a Parameter. Adv Differ Equ 2010, 971540 (2010). https://doi.org/10.1155/2010/971540
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/971540
 and
and  ;
;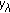 is nondecreasing in
is nondecreasing in 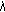 ;
;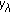 is continuous in
is continuous in 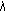 , that is, if
, that is, if  , then
, then  .
.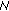 such that
such that 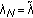 . In this case, we have
. In this case, we have 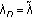 for all
for all 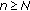 holds. Hence, for
holds. Hence, for  , it follows from (3.4) and the mixed monotonicity of
, it follows from (3.4) and the mixed monotonicity of  that
that 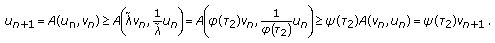
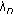 , we have
, we have
 ,
,  . In this case, we have
. In this case, we have 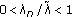 . In accordance with
. In accordance with 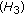 , there exists
, there exists  such that
such that  . Hence, combining (3.4) with the mixed monotonicity of
. Hence, combining (3.4) with the mixed monotonicity of 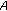 , we have
, we have 
 is nonincreasing with respect to
is nonincreasing with respect to 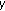 , and there exists
, and there exists  such that
such that
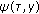 is nondecreasing with respect to
is nondecreasing with respect to  , and there exists
, and there exists 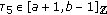 such that
such that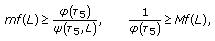
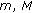 are defined in (2.1),
are defined in (2.1), 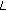 is defined in (3.5). Then, the BVP
is defined in (3.5). Then, the BVP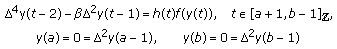
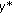 .
. -Laplacian difference equations. Computers & Mathematics with Applications 2008,55(9):1943-1949. 10.1016/j.camwa.2007.08.033
-Laplacian difference equations. Computers & Mathematics with Applications 2008,55(9):1943-1949. 10.1016/j.camwa.2007.08.033 -
- -concave operators and applications. Computers and Mathematics with Applications 2010,59(1):532-538. 10.1016/j.camwa.2009.06.016
-concave operators and applications. Computers and Mathematics with Applications 2010,59(1):532-538. 10.1016/j.camwa.2009.06.016