- Research Article
- Open access
- Published:
Dynamics of a Rational Difference Equation
Advances in Difference Equations volume 2010, Article number: 970720 (2010)
Abstract
The main goal of the paper is to investigate boundedness, invariant intervals, semicycles, and global attractivity of all nonnegative solutions of the equation  ,
,  , where the parameters
, where the parameters  ,
,  is an integer, and the initial conditions
is an integer, and the initial conditions  . It is shown that the unique positive equilibrium of the equation is globally asymptotically stable under the condition
. It is shown that the unique positive equilibrium of the equation is globally asymptotically stable under the condition  . The result partially solves the open problem proposed by Kulenović and Ladas in work (2002).
. The result partially solves the open problem proposed by Kulenović and Ladas in work (2002).
1. Introduction
The aim of this paper is to study the dynamical behavior of the following rational difference equation:

where  is an integer, and the initial conditions
is an integer, and the initial conditions  The related case where
The related case where  was investigated in [1].
was investigated in [1].
In 2002, Kulenović and Ladas [1] proposed the following open problem.
Open Problem 1.
Assume that  and
and  . Investigate the global behavior of all positive solutions of (1.1).
. Investigate the global behavior of all positive solutions of (1.1).
If we allow the parameters to be satisfied,  , then (1.1) contains, as special cases, six difference equations with positive parameters:
, then (1.1) contains, as special cases, six difference equations with positive parameters:






Equations (1.2) and (1.3) can be reduced to (1.5), which was studied in [2]. By the change of variables  , equation (1.4) can be reduced to the linear equation
, equation (1.4) can be reduced to the linear equation

whose global behavior of solutions is easily derived. Equation (1.6) is investigated in [3].
Equation (1.7) is essentially similar to the Riccati equation. In fact, if  is a positive solution of (1.7), then
is a positive solution of (1.7), then  are
are  solutions of the following Riccati equations:
solutions of the following Riccati equations:

respectively.
Therefore, we only pay attention to investigating (1.1) with positive parameters and omit any further discussion of the above (1.2)–(1.7).
For other related results on difference equations, one can refer to [4–18].
Equation (1.1) has a unique equilibrium  which is positive and is given by
which is positive and is given by

In [19], the authors investigated the global asymptotic stability of the positive equilibrium  of (1.1). We summarize their results in the following theorem.
of (1.1). We summarize their results in the following theorem.
Theorem 1.1.
-
(i)
Assume that
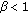 . Then the positive equilibrium
. Then the positive equilibrium  of (1.1) is locally asymptotically stable.
of (1.1) is locally asymptotically stable. -
(ii)
Assume that
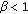 and
and 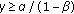 . Then for every solution of (1.1) with initial conditions in invariant interval
. Then for every solution of (1.1) with initial conditions in invariant interval  , the positive equilibrium point
, the positive equilibrium point  is globally asymptotically stable.
is globally asymptotically stable. -
(iii)
Assume that
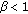 and
and  . Then for every solution of (1.1) with initial conditions in invariant interval
. Then for every solution of (1.1) with initial conditions in invariant interval 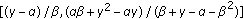 , the positive equilibrium point
, the positive equilibrium point  is globally asymptotically stable.
is globally asymptotically stable.
Reviewing the proof of Theorem 1.1, one can easily find that the positive equilibrium  of (1.1) is locally asymptotically stable when
of (1.1) is locally asymptotically stable when  . So Theorem 1.1 (i) can be improved as the following theorem.
. So Theorem 1.1 (i) can be improved as the following theorem.
Theorem 1.2.
Assume that  . Then the positive equilibrium
. Then the positive equilibrium  of (1.1) is locally asymptotically stable.
of (1.1) is locally asymptotically stable.
By the change of variables  , (1.1) reduces to the difference equation
, (1.1) reduces to the difference equation

where  , and
, and  Its unique positive equilibrium is
Its unique positive equilibrium is

Motivated by the above open problem, the purpose of this paper is to investigate the boundedness, local stability, invariant intervals, semicycles, and global attractivity of all nonnegative solutions of (1.11). We show that the unique positive equilibrium of (1.11) is a global attractor when  and our result solves the open problem when
and our result solves the open problem when  .
.
The organization of this paper is as follows. In Section 2, some basic definitions and lemmas regarding difference equations are given. The boundedness and invariant intervals of (1.11) are discussed in Section 3. The semicycle analysis of (1.11) is presented in Section 4. The main results are formulated and proved in Section 5, where the global asymptotic stability of (1.11) is investigated.
2. Some Lemmas
In this section, we recall some definitions and lemmas which will be useful in the sequel.
Let  be some interval of real numbers and let
be some interval of real numbers and let  be a continuously differentiable function. Then for initial conditions
be a continuously differentiable function. Then for initial conditions  , the difference equation
, the difference equation

has a unique solution  .
.
An internal is called an invariant interval of (2.1) if
is called an invariant interval of (2.1) if

That is, every solution of (2.1) with initial conditions in  remains in
remains in  .
.
Definition 2.1.
Let  be an equilibrium point of (2.1).
be an equilibrium point of (2.1).
-
(i)
The equilibrium point
 of (2.1) is called locally stable if for every
of (2.1) is called locally stable if for every 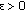 there exists
there exists 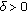 such that for all
such that for all  with
with 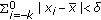 , one has
, one has 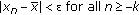 .
. -
(ii)
The equilibrium point
 of (2.1) is called locally asymptotically stable if it is locally stable and if there exists
of (2.1) is called locally asymptotically stable if it is locally stable and if there exists 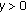 such that for all
such that for all 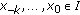 with
with 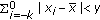 one has
one has 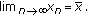
-
(iii)
The equilibrium point
 of (2.1) is called a global attractor if for every
of (2.1) is called a global attractor if for every 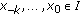 one has
one has 
-
(iv)
The equilibrium point
 of (2.1) is called globally asymptotically stable if it is locally asymptotically stable and is a global attractor.
of (2.1) is called globally asymptotically stable if it is locally asymptotically stable and is a global attractor. -
(v)
The equilibrium point
 of (2.1) is called unstable if it is not locally stable.
of (2.1) is called unstable if it is not locally stable.
The following lemmas can be found in [3, 20], respectively; also see [19, 21–24].
Lemma 2.2 (see [3]).
Let  be an interval of real numbers and assume that
be an interval of real numbers and assume that  is a continuous function satisfying the following properties.
is a continuous function satisfying the following properties.
-
(i)
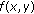 is nondecreasing in each of its arguments.
is nondecreasing in each of its arguments. -
(i)
(ii)The equation
 (2.3)
(2.3)has a unique positive solution in the interval
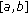 .
.
Then (2.1) has a unique positive equilibrium  and every solution of (2.1) converges to
and every solution of (2.1) converges to  .
.
Lemma 2.3 (see [20]).
Let  be an interval of real numbers and assume that
be an interval of real numbers and assume that  is a continuous function satisfying the following properties.
is a continuous function satisfying the following properties.
-
(i)
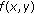 is a nondecreasing function in
is a nondecreasing function in  and a nonincreasing function in
and a nonincreasing function in  .
. -
(ii)
If
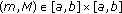 is a solution of the following system:
is a solution of the following system: (2.4)
(2.4)then
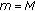 .
.
Then (2.1) has a unique equilibrium point  and every solution of (2.1) converges to
and every solution of (2.1) converges to  .
.
The following result was proved in [25].
Lemma 2.4 (see [25]).
Assume that  and
and  hold. Then the positive equilibrium
hold. Then the positive equilibrium  of the difference equation
of the difference equation

is a global attractor of all positive solutions.
3. Boundedness and Invariant Intervals
The following result about boundedness of (1.11) can be found in [19].
Theorem 3.1.
Every solution of (1.11) is bounded from above and from below by positive constants.
Let  be a nonnegative solution of (1.11). Then the following identities are easily established:
be a nonnegative solution of (1.11). Then the following identities are easily established:




If  , then the unique equilibrium is
, then the unique equilibrium is  and (3.1) and (3.4) become
and (3.1) and (3.4) become


respectively.
If  , then the unique equilibrium is
, then the unique equilibrium is  and (3.4) becomes
and (3.4) becomes

Set

Then we have the following monotone character for the function  .
.
Lemma 3.2.
Let  be defined by (3.8). Then the following statements hold true.
be defined by (3.8). Then the following statements hold true.
-
(i)
Assume that
 . Then
. Then 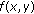 is strictly increasing in each of its arguments for
is strictly increasing in each of its arguments for  and it is strictly increasing in
and it is strictly increasing in  and decreasing in
and decreasing in  for
for  .
. -
(ii)
Assume that
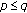 . Then
. Then 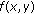 is strictly increasing in
is strictly increasing in  and decreasing in
and decreasing in 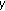 for
for  .
.
Proof.
By calculating, the partial derivatives of the function  are
are

from which (i) and (ii) easily follow.
3.1. The Case 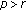
Lemma 3.3.
Assume that  and
and  is a nonnegative solution of (1.11). Then the following statements are true.
is a nonnegative solution of (1.11). Then the following statements are true.
-
(i)
If for some
 , then
, then  for
for 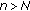 .
. -
(ii)
If for some
 , then
, then  .
. -
(iii)
If for some
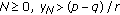 , then
, then 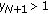 .
. -
(iv)
If for some
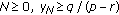 , then
, then  for
for  .
. -
(v)
If for some
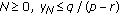 , then
, then 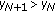 .
. -
(vi)
If for some
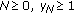 , then
, then  .
. -
(vii)
Equation (1.11) possesses an invariant interval
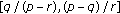 and
and  ; moreover, the interval
; moreover, the interval  is also an invariant interval of (1.11) and
is also an invariant interval of (1.11) and 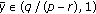 .
.
Proof.
-
(i)–(vi)
Clearly, in this case
 holds. The statements directly follow by using the identities (3.1), (3.3) and (3.4).
holds. The statements directly follow by using the identities (3.1), (3.3) and (3.4). -
(vii)
By Lemma 3.2 (i) the function
 is strictly increasing in each of its arguments for
is strictly increasing in each of its arguments for 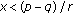 . Given that
. Given that 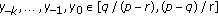 , then we get
, then we get 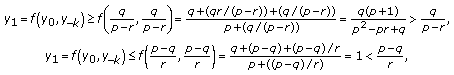 (3.10)
(3.10)which implies that
 . By the induction,
. By the induction,  for every
for every 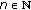 , as claimed.
, as claimed.
On the other hand,  implies that
implies that

Furthermore,  is the unique positive root of the quadratic equation
is the unique positive root of the quadratic equation

Since

then we have that  . That is,
. That is,  , finishing the proof.
, finishing the proof.
When  , identities (3.5) and (3.6) imply that the following results hold.
, identities (3.5) and (3.6) imply that the following results hold.
Lemma 3.4.
Assume that  and
and  is a nonnegative solution of (1.11). Then the following statements are true.
is a nonnegative solution of (1.11). Then the following statements are true.
-
(i)
If for some
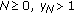 , then
, then 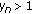 for
for  .
. -
(ii)
If for some
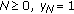 , then
, then 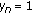 for
for 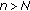 .
. -
(iii)
If for some
 , then
, then  for
for 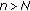 .
. -
(iv)
If for some
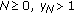 , then
, then  .
. -
(v)
If for some
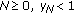 , then
, then 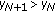 .
.
Lemma 3.5.
Assume that  holds and
holds and  is a nonnegative solution of equation (1.11). Then the following statements are true
is a nonnegative solution of equation (1.11). Then the following statements are true
-
(i)
If for some
 , then
, then 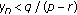 for
for 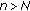 .
. -
(ii)
If for some
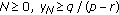 , then
, then 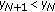 .
. -
(iii)
If for some
 , then
, then  .
. -
(iv)
Equation (1.11) possesses an invariant interval
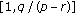 and
and  . Further, if
. Further, if 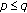 , then
, then  for all
for all  , and if
, and if  , then the following statements are also true.
, then the following statements are also true. -
(v)
If for some
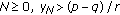 , then
, then  for
for  .
. -
(vi)
If for some
 , then
, then 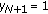 .
. -
(vii)
If for some
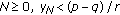 , then
, then 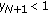 .
.
Proof.
In this case  holds.
holds.
-
(i)–(iii)
Using the identities (3.3) and (3.4), one can see that the results follow.
-
(iv)
By Lemma 3.2 the function
 is strictly increasing in
is strictly increasing in  and decreasing in
and decreasing in 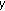 in
in 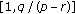 . Then we can get
. Then we can get  (3.14)
(3.14)
which implies that  . By the induction,
. By the induction,  for every
for every  .
.
On the other hand,  implies that
implies that

Then as same as the argument in Lemma 3.3 (vii) it can be proved that  .
.
Further, if  , then the identity (3.1) implies that
, then the identity (3.1) implies that  for all
for all  , and if
, and if  , the results (v)–(vii) can also follow from (3.1).
, the results (v)–(vii) can also follow from (3.1).
The proof is complete.
3.2. The Case 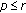
Lemma 3.6.
Assume that  . Then the interval
. Then the interval  is an invariant interval of (1.11) and
is an invariant interval of (1.11) and  . Further, if
. Further, if  , then the following statements are also true.
, then the following statements are also true.
-
(i)
If for some
 , then
, then  for
for 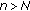 .
. -
(ii)
If for some
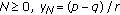 , then
, then 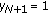 .
. -
(iii)
If for some
 , then
, then  .
.
Proof.
Notice that in this case the inequality  holds; then the results can easily be obtained by using the identity (3.1). Further,
holds; then the results can easily be obtained by using the identity (3.1). Further,  implies that
implies that

finishing the proof.
4. Semicycle Analysis
Here, we present some results regarding the semicycle analysis of the solutions of (1.11). Now recall two definitions from [25].
Definition 4.1.
Let  be a solution of (2.1). A positive semicycle of the solution
be a solution of (2.1). A positive semicycle of the solution  of (2.1) consists of a "string" of terms
of (2.1) consists of a "string" of terms  , all greater than or equal to the equilibrium point
, all greater than or equal to the equilibrium point  , with
, with  and
and  such that
such that

Definition 4.2.
Let  be a solution of (2.1). A negative semicycle of the solution
be a solution of (2.1). A negative semicycle of the solution  of (2.1) consists of a "string" of terms
of (2.1) consists of a "string" of terms  , all less than the equilibrium point
, all less than the equilibrium point  , with
, with  and
and  such that
such that

The next two lemmas can be found in [26] and [19], respectively.
Lemma 4.3 (see [26]).
Assume that  and that
and that  is increasing in both arguments. Let
is increasing in both arguments. Let  be a positive equilibrium of (2.1). Then except possibly for the first semicycle, every oscillatory solution of (2.1) has semicycles of length at most
be a positive equilibrium of (2.1). Then except possibly for the first semicycle, every oscillatory solution of (2.1) has semicycles of length at most  .
.
Lemma 4.4 (see [19]).
Assume that  and that
and that  is increasing in
is increasing in  for each fixed
for each fixed  and is decreasing in
and is decreasing in  for each fixed
for each fixed  . Let
. Let  be a positive equilibrium of (2.1). If
be a positive equilibrium of (2.1). If  , then every oscillatory solution of (2.1) has semicycles that are either of length at least
, then every oscillatory solution of (2.1) has semicycles that are either of length at least  or of length at most
or of length at most  .
.
Using the monotonic character of the function  from Lemma 3.2, in each of the intervals in Lemmas 3.3–3.6, together with Lemmas 4.3 and 4.4, it is easy to obtain the following results concerning semicycle analysis.
from Lemma 3.2, in each of the intervals in Lemmas 3.3–3.6, together with Lemmas 4.3 and 4.4, it is easy to obtain the following results concerning semicycle analysis.
Theorem 4.5.
Assume that  and
and  is a nonnegative solution of (1.11). Then the following statements are true.
is a nonnegative solution of (1.11). Then the following statements are true.
-
(i)
If
 , then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval
, then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval 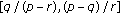 has semicycles of length at most
has semicycles of length at most 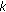 .
. -
(ii)
If
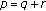 , then (1.11) does not have oscillatory solution with
, then (1.11) does not have oscillatory solution with  or
or 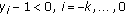 .
. -
(iii)
If
 , then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval
, then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval 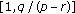 has semicycles that are either of length at least
has semicycles that are either of length at least  or of length at most
or of length at most  .
.
Theorem 4.6.
Assume that  and
and  is a nonnegative solution of (1.11). Then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval
is a nonnegative solution of (1.11). Then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval  has semicycles that are either of length at least
has semicycles that are either of length at least  or of length at most
or of length at most  .
.
5. Global Asymptotic Stability for the Case 
In this section, we discuss the global attractivity of the positive equilibrium of (1.11). We show that  is a global attractor of all nonnegative solutions of (1.11) when
is a global attractor of all nonnegative solutions of (1.11) when  . Further, the unique positive equilibrium
. Further, the unique positive equilibrium  of (1.1) is globally asymptotically stable when
of (1.1) is globally asymptotically stable when  .
.
Theorem 5.1.
Assume that  . Then the unique positive equilibrium
. Then the unique positive equilibrium  of (1.11) is a global attractor.
of (1.11) is a global attractor.
The proof is finished by considering the following four cases; see Theorems 5.3, 5.5, 5.7, and 5.9.
Theorem 5.2.
Assume that  holds, and
holds, and  is a nonnegative solution of (1.11). If
is a nonnegative solution of (1.11). If  , then
, then  for
for  . Furthermore, every nonnegative solution of (1.11) lies eventually in the interval
. Furthermore, every nonnegative solution of (1.11) lies eventually in the interval  .
.
Proof.
Firstly, note that in this case  holds.
holds.
If  , then by Lemma 3.3 (i) and (iv), we have that
, then by Lemma 3.3 (i) and (iv), we have that  for
for  , the first assertion follows.
, the first assertion follows.
To complete the proof it remains to show that when  there exists
there exists  such that
such that  . There are two cases to be considered.
. There are two cases to be considered.
Case 1 ( ).
).
Lemma 3.3 (ii) and (iii) implies that  . If
. If  , then the proof follows from the first assertion. Now assume for the sake of contradiction that all terms of
, then the proof follows from the first assertion. Now assume for the sake of contradiction that all terms of  never enter the interval
never enter the interval  ; then
; then  would lie in the interval
would lie in the interval  for
for  . Using Lemma 3.3 (vi), we obtain
. Using Lemma 3.3 (vi), we obtain  for
for  , from which it follows that the sequence
, from which it follows that the sequence  is strictly decreasing in the interval
is strictly decreasing in the interval  . Hence,
. Hence,  exists and
exists and  , which is a contradiction, because, in view of Lemma 3.3 (vii), (1.11) has no equilibrium points in the interval
, which is a contradiction, because, in view of Lemma 3.3 (vii), (1.11) has no equilibrium points in the interval  .
.
Case 2 ( ).
).
If there exists  such that
such that  , then the proof follows from the first assertion. If there exists
, then the proof follows from the first assertion. If there exists  such that
such that  , then the proof also follows from Case 1. Now assume for the sake of contradiction that
, then the proof also follows from Case 1. Now assume for the sake of contradiction that  for all
for all  , then by Lemma 3.3 (v), we have that
, then by Lemma 3.3 (v), we have that  for
for  , which means that
, which means that  exists and
exists and  ; this contradicts Lemma 3.3 (vii).
; this contradicts Lemma 3.3 (vii).
The proof is complete.
Theorem 5.3.
Assume that  holds. Then the unique positive equilibrium
holds. Then the unique positive equilibrium  of (1.11) is a global attractor of all nonnegative solutions of (1.11).
of (1.11) is a global attractor of all nonnegative solutions of (1.11).
Proof.
Theorem 5.2 and Lemma 3.3 (vii) imply that every nonnegative solution of (1.11) eventually enters the interval  . Furthermore, the function
. Furthermore, the function  is increasing in each of its arguments in
is increasing in each of its arguments in  and the equation
and the equation

has a unique positive solution on the interval  . The proof now immediately follows by applying Lemma 2.2.
. The proof now immediately follows by applying Lemma 2.2.
Theorem 5.4.
Assume that  , and
, and  is a nontrivial nonnegative solution of (1.11). Then the sequence
is a nontrivial nonnegative solution of (1.11). Then the sequence  is monotonic and
is monotonic and  .
.
Proof.
In this case, the unique positive equilibrium is  . By Lemma 3.4 it easy to see that if
. By Lemma 3.4 it easy to see that if  then
then  is decreasing and bounded below by 1, if
is decreasing and bounded below by 1, if  then
then  is increasing and bounded above by 1, and if
is increasing and bounded above by 1, and if  then
then  for
for  . Hence, in all case the sequence
. Hence, in all case the sequence  converges to 1, as desired.
converges to 1, as desired.
By Theorem 5.4, it is easy to see that the following result is true.
Theorem 5.5.
Assume that  . Then the unique positive equilibrium
. Then the unique positive equilibrium  is a global attractor of all nonnegative solutions of (1.11).
is a global attractor of all nonnegative solutions of (1.11).
Theorem 5.6.
Assume that  holds and
holds and  is a nonnegative solution of (1.11). If
is a nonnegative solution of (1.11). If  , then
, then  for
for  . Furthermore, every nonnegative solution of (1.11) lies eventually in the interval
. Furthermore, every nonnegative solution of (1.11) lies eventually in the interval  .
.
Proof.
Firstly, note that in this case  holds.
holds.
If  , then by Lemma 3.5 (iv) and (i), we have that
, then by Lemma 3.5 (iv) and (i), we have that  for
for  ; the first assertion follows.
; the first assertion follows.
To complete the proof it remains to show that when  there exists
there exists  such that
such that  . There are two cases to be considered.
. There are two cases to be considered.
Case 1 ( ).
).
Lemma 3.5 (i) implies that  for
for  . If there exists
. If there exists  such that
such that  , then the proof follows from the first assertion. Now assume for the sake of contradiction that all terms of
, then the proof follows from the first assertion. Now assume for the sake of contradiction that all terms of  never enter the interval
never enter the interval  , then
, then  would lie in the interval
would lie in the interval  for
for  . Using Lemma 3.5 (iii), we obtain that
. Using Lemma 3.5 (iii), we obtain that  for
for  , from which it follows that
, from which it follows that  exists and
exists and  , which is a contradiction, because in view of Lemma 3.5 (iv), (1.11) has no equilibrium points in the interval
, which is a contradiction, because in view of Lemma 3.5 (iv), (1.11) has no equilibrium points in the interval  .
.
Case 2 ( ).
).
If there exists  such that
such that  , then the proof follows from the first assertion. If there exists
, then the proof follows from the first assertion. If there exists  such that
such that  , then the proof also follows from Case 1. Now assume for the sake of contradiction that
, then the proof also follows from Case 1. Now assume for the sake of contradiction that  for all
for all  , then by Lemma 3.5 (ii), we have that
, then by Lemma 3.5 (ii), we have that  for
for  , from which it follows that
, from which it follows that  exists and
exists and  . This contradicts Lemma 3.5 (iv).
. This contradicts Lemma 3.5 (iv).
The proof is complete.
Theorem 5.7.
Assume that  holds. Then the unique positive equilibrium
holds. Then the unique positive equilibrium  of (1.11) is a global attractor of all nonnegative solutions of (1.11).
of (1.11) is a global attractor of all nonnegative solutions of (1.11).
Proof.
Theorem 5.6 implies that every nonnegative solution of (1.11) lies eventually in the invariant interval  .
.
Further, the function  is nondecreasing in
is nondecreasing in  and nonincreasing in
and nonincreasing in  in
in  . Let
. Let  be a solution of the system
be a solution of the system

then  , from which we get that
, from which we get that  , and the proof now follows by applying Lemma 2.3.
, and the proof now follows by applying Lemma 2.3.
Theorem 5.8.
Assume that  holds and that
holds and that  is a nonnegative solution of (1.11). Then every nonnegative solution of (1.11) lies eventually in the invariant interval
is a nonnegative solution of (1.11). Then every nonnegative solution of (1.11) lies eventually in the invariant interval  .
.
Proof.
When  ,
,

Hence the assertion is true for the case  . There remains to consider the case
. There remains to consider the case  . In this case
. In this case  holds.
holds.
If  , then by Lemma 3.6 (i) and (ii), we have that
, then by Lemma 3.6 (i) and (ii), we have that  for
for  , and the assertion follows.
, and the assertion follows.
Given that  , then by Lemma 3.6 (iii), we have that
, then by Lemma 3.6 (iii), we have that  . If
. If  , then the assertion is true from the above proof. Now assume for the sake of contradiction that
, then the assertion is true from the above proof. Now assume for the sake of contradiction that  for all
for all  . Using identity (3.7), we get that
. Using identity (3.7), we get that  for
for  , from which it follows that the sequence
, from which it follows that the sequence  is strictly increasing and there is a finite
is strictly increasing and there is a finite  ; this contradicts the fact that
; this contradicts the fact that  .
.
The proof is complete.
Theorem 5.9.
Assume that  holds. Then the unique positive equilibrium
holds. Then the unique positive equilibrium  of (1.11) is a global attractor of all nonnegative solutions of (1.11).
of (1.11) is a global attractor of all nonnegative solutions of (1.11).
Proof.
Theorem 5.8 implies that there exist a positive integer  such that
such that  for
for  . Therefore the change of variables
. Therefore the change of variables

transforms (1.11) to the difference equation

Clearly,  and
and  hold, and the remainder proof now is a straightforward consequence of Lemma 2.4.
hold, and the remainder proof now is a straightforward consequence of Lemma 2.4.
In view of Theorem 5.1, we know that the unique positive equilibrium  of (1.1) is a global attractor when
of (1.1) is a global attractor when  . From this and Theorem 1.2, we have the following main result, which partially solves Open Problem 1.
. From this and Theorem 1.2, we have the following main result, which partially solves Open Problem 1.
Theorem 5.10.
Assume that  . Then the unique positive equilibrium
. Then the unique positive equilibrium  of (1.1) is globally asymptotically stable.
of (1.1) is globally asymptotically stable.
References
Kulenović MRS, Ladas G: Dynamics of Second Order Rational Difference Equations with Open Problem and Conjectures. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xii+218.
Dehghan M, Mazrooei-Sebdani R: Dynamics of a higher-order rational difference equation. Applied Mathematics and Computation 2006,178(2):345-354. 10.1016/j.amc.2005.11.059
Li W-T, Sun H-R: Dynamics of a rational difference equation. Applied Mathematics and Computation 2005,163(2):577-591. 10.1016/j.amc.2004.04.002
Agarwal RP, Li W-T, Pang PYH: Asymptotic behavior of a class of nonlinear delay difference equations. Journal of Difference Equations and Applications 2002,8(8):719-728. 10.1080/1023619021000000735
Amleh AM, Camouzis E, Ladas G: On the boundedness character of rational equations. II. Journal of Difference Equations and Applications 2006,12(6):637-650. 10.1080/10236190500539279
Chen D, Li X, Wang Y:Dynamics for nonlinear difference equation
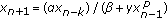 . Advances in Difference Equations 2009, 2009:-13.
. Advances in Difference Equations 2009, 2009:-13.Gibbons GH, Kulenović MRS, Ladas G:On the dynamics of
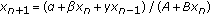 . In New Trends in Difference Equations. Taylor & Francis, London, UK; 2002:141-158.
. In New Trends in Difference Equations. Taylor & Francis, London, UK; 2002:141-158.Hu L-X, Li W-T, Stević S: Global asymptotic stability of a second order rational difference equation. Journal of Difference Equations and Applications 2008,14(8):779-797. 10.1080/10236190701827945
Hu L-X, Li W-T, Xu H-W: Global asymptotical stability of a second order rational difference equation. Computers & Mathematics with Applications 2007,54(9-10):1260-1266. 10.1016/j.camwa.2007.03.013
Huang YS, Knopf PM: Boundedness of positive solutions of second-order rational difference equations. Journal of Difference Equations and Applications 2004,10(11):935-940. 10.1080/10236190412331285360
Kocić VL, Ladas G, Rodrigues IW: On rational recursive sequences. Journal of Mathematical Analysis and Applications 1993,173(1):127-157. 10.1006/jmaa.1993.1057
Kulenović MRS, Ladas G, Martins LF, Rodrigues IW:The dynamics of
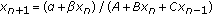 : facts and conjectures. Computers & Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7
: facts and conjectures. Computers & Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7Li W, Zhang Y, Su Y: Global attractivity in a class of higher-order nonlinear difference equation. Acta Mathematica Scientia 2005,25(1):59-66.
Stević S:On the difference equation
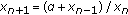 . Computers & Mathematics with Applications 2008,56(5):1159-1171. 10.1016/j.camwa.2008.02.017
. Computers & Mathematics with Applications 2008,56(5):1159-1171. 10.1016/j.camwa.2008.02.017Stević S: Global stability and asymptotics of some classes of rational difference equations. Journal of Mathematical Analysis and Applications 2006,316(1):60-68. 10.1016/j.jmaa.2005.04.077
Su Y-H, Li W-T, Stević S: Dynamics of a higher order nonlinear rational difference equation. Journal of Difference Equations and Applications 2005,11(2):133-150. 10.1080/10236190512331319352
Su YH, Li WT: Global asymptotic stability for a higher order nonlinear difference equations. Journal of Difference Equations and Applications 2005, 11: 947-958. 10.1080/10236190500273333
Yan X-X, Li W-T, Zhao Z: Global asymptotic stability for a higher order nonlinear rational difference equations. Applied Mathematics and Computation 2006,182(2):1819-1831. 10.1016/j.amc.2006.06.019
Dehghan M, Rastegar N: On the global behavior of a high-order rational difference equation. Computer Physics Communications 2009,180(6):873-878. 10.1016/j.cpc.2008.12.006
DeVault R, Kosmala W, Ladas G, Schultz SW:Global behavior of
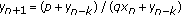 . Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4743-4751. 10.1016/S0362-546X(01)00586-7
. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4743-4751. 10.1016/S0362-546X(01)00586-7Camouzis E, Ladas G: Dynamics of Third-Order Rational Difference Equations with Open Problems and Conjectures, Advances in Discrete Mathematics and Applications. Volume 5. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2008:xxii+554.
Jaberi Douraki M, Dehghan M, Mashreghi J:Dynamics of the difference equation
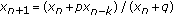 . Computers & Mathematics with Applications 2008,56(1):186-198. 10.1016/j.camwa.2007.06.029
. Computers & Mathematics with Applications 2008,56(1):186-198. 10.1016/j.camwa.2007.06.029Mazrooei-Sebdani R, Dehghan M: The study of a class of rational difference equations. Applied Mathematics and Computation 2006,179(1):98-107. 10.1016/j.amc.2005.11.083
Saleh M, Abu-Baha S: Dynamics of a higher order rational difference equation. Applied Mathematics and Computation 2006,181(1):84-102. 10.1016/j.amc.2006.01.012
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+228.
Mazrooei-Sebdani R, Dehghan M: Dynamics of a non-linear difference equation. Applied Mathematics and Computation 2006,178(2):250-261. 10.1016/j.amc.2005.11.042
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jia, XM., Hu, LX. & Li, WT. Dynamics of a Rational Difference Equation. Adv Differ Equ 2010, 970720 (2010). https://doi.org/10.1155/2010/970720
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/970720
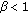 . Then the positive equilibrium
. Then the positive equilibrium  of (1.1) is locally asymptotically stable.
of (1.1) is locally asymptotically stable.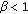 and
and 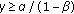 . Then for every solution of (1.1) with initial conditions in invariant interval
. Then for every solution of (1.1) with initial conditions in invariant interval  , the positive equilibrium point
, the positive equilibrium point  is globally asymptotically stable.
is globally asymptotically stable.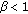 and
and  . Then for every solution of (1.1) with initial conditions in invariant interval
. Then for every solution of (1.1) with initial conditions in invariant interval 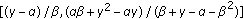 , the positive equilibrium point
, the positive equilibrium point  is globally asymptotically stable.
is globally asymptotically stable. of (2.1) is called locally stable if for every
of (2.1) is called locally stable if for every 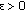 there exists
there exists 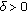 such that for all
such that for all  with
with 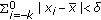 , one has
, one has 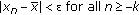 .
. of (2.1) is called locally asymptotically stable if it is locally stable and if there exists
of (2.1) is called locally asymptotically stable if it is locally stable and if there exists 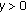 such that for all
such that for all 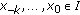 with
with 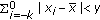 one has
one has 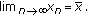
 of (2.1) is called a global attractor if for every
of (2.1) is called a global attractor if for every 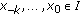 one has
one has 
 of (2.1) is called globally asymptotically stable if it is locally asymptotically stable and is a global attractor.
of (2.1) is called globally asymptotically stable if it is locally asymptotically stable and is a global attractor. of (2.1) is called unstable if it is not locally stable.
of (2.1) is called unstable if it is not locally stable.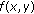 is nondecreasing in each of its arguments.
is nondecreasing in each of its arguments.
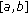 .
.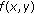 is a nondecreasing function in
is a nondecreasing function in  and a nonincreasing function in
and a nonincreasing function in  .
.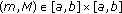 is a solution of the following system:
is a solution of the following system:
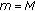 .
. . Then
. Then 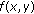 is strictly increasing in each of its arguments for
is strictly increasing in each of its arguments for  and it is strictly increasing in
and it is strictly increasing in  and decreasing in
and decreasing in  for
for  .
.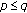 . Then
. Then 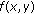 is strictly increasing in
is strictly increasing in  and decreasing in
and decreasing in 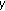 for
for  .
.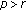
 , then
, then  for
for 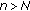 .
. , then
, then  .
.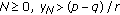 , then
, then 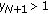 .
.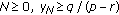 , then
, then  for
for  .
.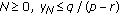 , then
, then 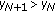 .
.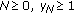 , then
, then  .
.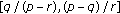 and
and  ; moreover, the interval
; moreover, the interval  is also an invariant interval of (1.11) and
is also an invariant interval of (1.11) and 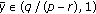 .
. holds. The statements directly follow by using the identities (3.1), (3.3) and (3.4).
holds. The statements directly follow by using the identities (3.1), (3.3) and (3.4). is strictly increasing in each of its arguments for
is strictly increasing in each of its arguments for 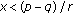 . Given that
. Given that 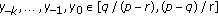 , then we get
, then we get 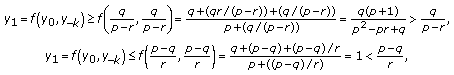
 . By the induction,
. By the induction,  for every
for every 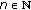 , as claimed.
, as claimed. , then
, then  for
for  .
.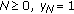 , then
, then 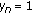 for
for 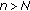 .
. , then
, then  for
for 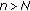 .
.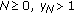 , then
, then  .
.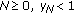 , then
, then 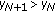 .
. , then
, then 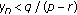 for
for 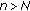 .
.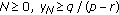 , then
, then 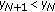 .
. , then
, then  .
.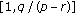 and
and  . Further, if
. Further, if 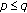 , then
, then  for all
for all  , and if
, and if  , then the following statements are also true.
, then the following statements are also true.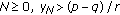 , then
, then  for
for  .
. , then
, then 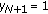 .
.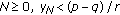 , then
, then 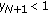 .
. is strictly increasing in
is strictly increasing in  and decreasing in
and decreasing in 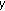 in
in 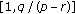 . Then we can get
. Then we can get 
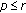
 , then
, then  for
for 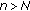 .
.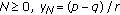 , then
, then 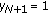 .
. , then
, then  .
. , then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval
, then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval 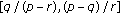 has semicycles of length at most
has semicycles of length at most 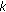 .
.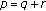 , then (1.11) does not have oscillatory solution with
, then (1.11) does not have oscillatory solution with  or
or 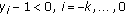 .
. , then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval
, then, except possibly for the first semicycle, every oscillatory solution of (1.11) which lies in the invariant interval 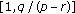 has semicycles that are either of length at least
has semicycles that are either of length at least  or of length at most
or of length at most  .
.
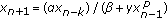 . Advances in Difference Equations 2009, 2009:-13.
. Advances in Difference Equations 2009, 2009:-13.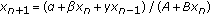 . In New Trends in Difference Equations. Taylor & Francis, London, UK; 2002:141-158.
. In New Trends in Difference Equations. Taylor & Francis, London, UK; 2002:141-158.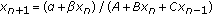 : facts and conjectures. Computers & Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7
: facts and conjectures. Computers & Mathematics with Applications 2003,45(6–9):1087-1099. 10.1016/S0898-1221(03)00090-7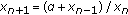 . Computers & Mathematics with Applications 2008,56(5):1159-1171. 10.1016/j.camwa.2008.02.017
. Computers & Mathematics with Applications 2008,56(5):1159-1171. 10.1016/j.camwa.2008.02.017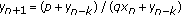 . Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4743-4751. 10.1016/S0362-546X(01)00586-7
. Nonlinear Analysis: Theory, Methods & Applications 2001,47(7):4743-4751. 10.1016/S0362-546X(01)00586-7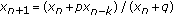 . Computers & Mathematics with Applications 2008,56(1):186-198. 10.1016/j.camwa.2007.06.029
. Computers & Mathematics with Applications 2008,56(1):186-198. 10.1016/j.camwa.2007.06.029