- Research Article
- Open access
- Published:
Some Results for Integral Inclusions of Volterra Type in Banach Spaces
Advances in Difference Equations volume 2010, Article number: 798067 (2010)
Abstract
We first present several existence results and compactness of solutions set for the following Volterra type integral inclusions of the form:  , where
, where  ,
,  is the infinitesimal generator of an integral resolvent family on a separable Banach space
is the infinitesimal generator of an integral resolvent family on a separable Banach space  , and
, and  is a set-valued map. Then the Filippov's theorem and a Filippov-Ważewski result are proved.
is a set-valued map. Then the Filippov's theorem and a Filippov-Ważewski result are proved.
1. Introduction
In the past few years, several papers have been devoted to the study of integral equations on real compact intervals under different conditions on the kernel (see, e.g., [1–4]) and references therein. However very few results are available for integral inclusions on compact intervals, see [5–7]. Topological structure of the solution set of integral inclusions of Volterra type is studied in [8].
In this paper we present some results on the existence of solutions, the compactness of set of solutions, Filippov's theorem, and relaxation for linear and semilinear integral inclusions of Volterra type of the form

where  and
and  is the generator of an integral resolvent family defined on a complex Banach space
is the generator of an integral resolvent family defined on a complex Banach space  , and
, and  is a multivalued map.
is a multivalued map.
In 1980, Da Prato and Iannelli introduced the concept of resolvent families, which can be regarded as an extension of  -semigroups in the study of a class of integrodifferential equations [9]. It is well known that the following abstract Volterra equation
-semigroups in the study of a class of integrodifferential equations [9]. It is well known that the following abstract Volterra equation

where  is a continuous function, is well-posed if and only if it admits a resolvent family, that is, there is a strongly continuous family
is a continuous function, is well-posed if and only if it admits a resolvent family, that is, there is a strongly continuous family  ,
,  , of bounded linear operators defined in
, of bounded linear operators defined in  , which commutes with
, which commutes with  and satisfies the resolvent equation
and satisfies the resolvent equation

The study of diverse properties of resolvent families such as the regularity, positivity, periodicity, approximation, uniform continuity, compactness, and others are studied by several authors under different conditions on the kernel and the operator  (see [10–24]). An important kernel is given by
(see [10–24]). An important kernel is given by

where

is the Riemann-Liouville kernel. In this case (1.1) and (1.2) can be represented in the form of fractional differential equations and inclusions or abstract fractional differential equations and inclusions. Also in the case where  , and
, and  is a Rieman-Liouville kernel, (1.1) and (1.2) can be represented in the form of fractional differential equations and inclusions, see for instants [25–27].
is a Rieman-Liouville kernel, (1.1) and (1.2) can be represented in the form of fractional differential equations and inclusions, see for instants [25–27].
Our goal in this paper is to complement and extend some recent results to the case of infinite-dimensional spaces; moreover the right-hand side nonlinearity may be either convex or nonconvex. Some auxiliary results from multivalued analysis, resolvent family theory, and so forth, are gathered together in Sections 2 and 3. In the first part of this work, we prove some existence results based on the nonlinear alternative of Leray-Schauder type (in the convex case), on Bressan-Colombo selection theorem and on the Covitz combined the nonlinear alternative of Leray-Schauder type for single-valued operators, and Covitz-Nadler fixed point theorem for contraction multivalued maps in a generalized metric space (in the nonconvex case). Some topological ingredients including some notions of measure of noncompactness are recalled and employed to prove the compactness of the solution set in Section 4.2. Section 5 is concerned with Filippov's theorem for the problem (1.1). In Section 6, we discuss the relaxed problem, namely, the density of the solution set of problem (1.1) in that of the convexified problem.
2. Preliminaries
In this section, we recall from the literature some notations, definitions, and auxiliary results which will be used throughout this paper. Let  be a separable Banach space,
be a separable Banach space,  an interval in
an interval in  and
and  the Banach space of all continuous functions from
the Banach space of all continuous functions from  into
into  with the norm
with the norm

 refers to the Banach space of linear bounded operators from
refers to the Banach space of linear bounded operators from  into
into  with norm
with norm

A function  is called measurable provided for every open subset
is called measurable provided for every open subset  , the set
, the set  is Lebesgue measurable. A measurable function
is Lebesgue measurable. A measurable function  is Bochner integrable if
is Bochner integrable if  is Lebesgue integrable. For properties of the Bochner integral, see, for example, Yosida [28]. In what follows,
is Lebesgue integrable. For properties of the Bochner integral, see, for example, Yosida [28]. In what follows,  denotes the Banach space of functions
denotes the Banach space of functions  , which are Bochner integrable with norm
, which are Bochner integrable with norm

Denote by  ,
,  closed},
closed},  bounded},
bounded},  convex},
convex},  compact
compact .
.
2.1. Multivalued Analysis
Let  and
and  be two metric spaces and
be two metric spaces and  be a multivalued map. A single-valued map
be a multivalued map. A single-valued map  is said to be a selection of
is said to be a selection of  and we write
and we write  whenever
whenever  for every
for every  .
.
 is called upper semicontinuous (u.s.c. for short) on
is called upper semicontinuous (u.s.c. for short) on  if for each
if for each  the set
the set  is a nonempty, closed subset of
is a nonempty, closed subset of  , and if for each open set
, and if for each open set  of
of  containing
containing  , there exists an open neighborhood
, there exists an open neighborhood  of
of  such that
such that  . That is, if the set
. That is, if the set  is closed for any closed set
is closed for any closed set  in
in  . Equivalently,
. Equivalently,  is u.s.c. if the set
is u.s.c. if the set  is open for any open set
is open for any open set  in
in  .
.
The following two results are easily deduced from the limit properties.
Lemma 2.1 (see, e.g., [29, Theorem 1.4.13]).
If  is u.s.c., then for any
is u.s.c., then for any  ,
,

Lemma 2.2 (see, e.g., [29, Lemma 1.1.9]).
Let  be a sequence of subsets where
be a sequence of subsets where  is compact in the separable Banach space
is compact in the separable Banach space  . Then
. Then

where  refers to the closure of the convex hull of
refers to the closure of the convex hull of  .
.
 is said to be completely continuous if it is u.s.c. and, for every bounded subset
is said to be completely continuous if it is u.s.c. and, for every bounded subset  ,
,  is relatively compact, that is, there exists a relatively compact set
is relatively compact, that is, there exists a relatively compact set  such that
such that  .
.  is compact if
is compact if  is relatively compact. It is called locally compact if, for each
is relatively compact. It is called locally compact if, for each  , there exists
, there exists  such that
such that  is relatively compact.
is relatively compact.  is quasicompact if, for each subset
is quasicompact if, for each subset  ,
,  is relatively compact.
is relatively compact.
Definition 2.3.
A multivalued map  is said measurable provided for every open
is said measurable provided for every open  , the set
, the set  is Lebesgue measurable.
is Lebesgue measurable.
We have
The mapping  is measurable if and only if for each
is measurable if and only if for each  , the function
, the function  defined by
defined by

is Lebesgue measurable.
The following two lemmas are needed in this paper. The first one is the celebrated Kuratowski-Ryll-Nardzewski selection theorem.
Lemma 2.5 (see [31, Theorem 19.7]).
Let  be a separable metric space and
be a separable metric space and  a measurable multivalued map with nonempty closed values. Then
a measurable multivalued map with nonempty closed values. Then  has a measurable selection.
has a measurable selection.
Lemma 2.6 (see [32, Lemma 3.2]).
Let  be a measurable multivalued map and
be a measurable multivalued map and  a measurable function. Then for any measurable
a measurable function. Then for any measurable  , there exists a measurable selection
, there exists a measurable selection  of
of  such that for a.e.
such that for a.e.  ,
,

Corollary 2.7.
Let  be a measurable multivalued map and
be a measurable multivalued map and  a measurable function. Then there exists a measurable selection
a measurable function. Then there exists a measurable selection  of
of  such that for a.e.
such that for a.e.  ,
,

2.1.1. Closed Graphs
We denote the graph of  to be the set
to be the set  .
.
Definition 2.8.
 is closed if
is closed if  is a closed subset of
is a closed subset of  , that is, for every sequences
, that is, for every sequences  and
and  , if
, if  ,
,  as
as  with
with , then
, then  .
.
We recall the following two results; the first one is classical.
Lemma 2.9 (see [33, Proposition 1.2]).
If  is u.s.c., then
is u.s.c., then  is a closed subset of
is a closed subset of  . Conversely, if
. Conversely, if  is locally compact and has nonempty compact values and a closed graph, then it is u.s.c.
is locally compact and has nonempty compact values and a closed graph, then it is u.s.c.
Lemma 2.10.
If  is quasicompact and has a closed graph, then
is quasicompact and has a closed graph, then  is u.s.c.
is u.s.c.
Given a separable Banach space  , for a multivalued map
, for a multivalued map  , denote
, denote

Definition 2.11.
A multivalued map  is called a Carathéodory function if
is called a Carathéodory function if
(a)the function  is measurable for each
is measurable for each  ;
;
(b)for a.e.  , the map
, the map  is upper semicontinuous.
is upper semicontinuous.
Furthermore,  is
is  -Carathéodory if it is locally integrably bounded, that is, for each positive
-Carathéodory if it is locally integrably bounded, that is, for each positive  , there exists
, there exists  such that
such that

For each  , the set
, the set

is known as the set of selection functions.
Remark 2.12.
-
(a)
For each
 , the set
, the set 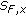 is closed whenever
is closed whenever  has closed values. It is convex if and only if
has closed values. It is convex if and only if 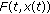 is convex for
is convex for  .
. -
(b)
From [34] (see also [35] when
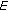 is finite-dimensional), we know that
is finite-dimensional), we know that  is nonempty if and only if the mapping
is nonempty if and only if the mapping  belongs to
belongs to  . It is bounded if and only if the mapping
. It is bounded if and only if the mapping  belongs to
belongs to  ; this particularly holds true when
; this particularly holds true when 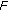 is
is 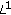 -Carathéodory. For the sake of completeness, we refer also to Theorem 1.3.5 in [36] which states that
-Carathéodory. For the sake of completeness, we refer also to Theorem 1.3.5 in [36] which states that 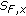 contains a measurable selection whenever
contains a measurable selection whenever  is measurable and
is measurable and  is a Carathéodory function.
is a Carathéodory function.
Lemma 2.13 (see [35]).
Given a Banach space  , let
, let  be an
be an  -Carathéodory multivalued map, and let
-Carathéodory multivalued map, and let  be a linear continuous mapping from
be a linear continuous mapping from  into
into  . Then the operator
. Then the operator

has a closed graph in  .
.
For further readings and details on multivalued analysis, we refer to the books by Andres and Górniewicz [37], Aubin and Cellina [38], Aubin and Frankowska [29], Deimling [33], Górniewicz [31], Hu and Papageorgiou [34], Kamenskii et al. [36], and Tolstonogov [39].
2.2. Semicompactness in 
Definition 2.14.
A sequence  is said to be semicompact if
is said to be semicompact if
-
(a)
it is integrably bounded, that is, there exists
 such that
such that (2.13)
(2.13) -
(b)
the image sequence
 is relatively compact in
is relatively compact in 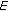 for a.e.
for a.e.  .
.
We recall two fundamental results. The first one follows from the Dunford-Pettis theorem (see [36, Proposition 4.2.1]). This result is of particular importance if  is reflexive in which case (a) implies (b) in Definition 2.14.
is reflexive in which case (a) implies (b) in Definition 2.14.
Lemma 2.15.
Every semicompact sequence  is weakly compact in
is weakly compact in  .
.
The second one is due to Mazur, 1933.
Lemma 2.16 (Mazur's Lemma, [28]).
Let  be a normed space and
be a normed space and  be a sequence weakly converging to a limit
be a sequence weakly converging to a limit  . Then there exists a sequence of convex combinations
. Then there exists a sequence of convex combinations  with
with  for
for  and
and  , which converges strongly to
, which converges strongly to  .
.
3. Resolvent Family
The Laplace transformation of a function  is defined by
is defined by

if the integral is absolutely convergent for  . In order to defined the mild solution of the problems (1.1) we recall the following definition.
. In order to defined the mild solution of the problems (1.1) we recall the following definition.
Definition 3.1.
Let  be a closed and linear operator with domain
be a closed and linear operator with domain  defined on a Banach space
defined on a Banach space  . We call
. We call  the generator of an integral resolvent if there exists
the generator of an integral resolvent if there exists  and a strongly continuous function
and a strongly continuous function  such that
such that

In this case,  is called the integral resolvent family generated by
is called the integral resolvent family generated by  .
.
The following result is a direct consequence of ([16, Proposition 3.1 and Lemma 2.2]).
Proposition 3.2.
Let  be an integral resolvent family with generator
be an integral resolvent family with generator  . Then the following conditions are satisfied
. Then the following conditions are satisfied
-
(a)
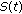 is strongly continuous for
is strongly continuous for  and
and  ;
; -
(b)
 and
and 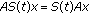 for all
for all  ;
; -
(c)
for every
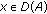 and
and 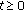 ,
, (3.3)
(3.3) -
(d)
let
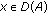 . Then
. Then  , and
, and (3.4)
(3.4)
In particular,  .
.
Remark 3.3.
The uniqueness of resolvent is well known (see Prüss [24]).
If an operator  with domain
with domain  is the infinitesimal generator of an integral resolvent family
is the infinitesimal generator of an integral resolvent family  and
and  is a continuous, positive and nondecreasing function which satisfies
is a continuous, positive and nondecreasing function which satisfies  , then for all
, then for all  we have
we have

(see [22, Theorem 2.1]). For example, the case  corresponds to the generator of a
corresponds to the generator of a  -semigroup and
-semigroup and  actually corresponds to the generator of a sine family; see [40]. A characterization of generators of integral resolvent families, analogous to the Hille-Yosida Theorem for
actually corresponds to the generator of a sine family; see [40]. A characterization of generators of integral resolvent families, analogous to the Hille-Yosida Theorem for  -semigroups, can be directly deduced from [22, Theorem 3.4]. More information on the
-semigroups, can be directly deduced from [22, Theorem 3.4]. More information on the  -semigroups and sine families can be found in [41–43].
-semigroups and sine families can be found in [41–43].
Definition 3.4.
A resolvent family of bounded linear operators,  , is called uniformly continuous if
, is called uniformly continuous if

Definition 3.5.
The solution operator  is called exponentially bounded if there are constants
is called exponentially bounded if there are constants  and
and  such that
such that

4. Existence Results
4.1. Mild Solutions
In order to define mild solutions for problem (1.1), we proof the following auxiliary lemma.
Lemma 4.1.
Let  . Assume that
. Assume that  generates an integral resolvent family
generates an integral resolvent family  on
on  , which is in addition integrable and
, which is in addition integrable and  . Let
. Let  be a continuous function (or
be a continuous function (or  ), then the unique bounded solution of the problem
), then the unique bounded solution of the problem

is given by

Proof.
Let  be a solution of the integral equation (4.2), then
be a solution of the integral equation (4.2), then

Using the fact that  is solution operator and Fubini's theorem we obtain
is solution operator and Fubini's theorem we obtain

Thus

This lemma leads us to the definition of a mild solution of the problem (1.1).
Definition 4.2.
A function  is said to be a mild solution of problem (1.1) if there exists
is said to be a mild solution of problem (1.1) if there exists  such that
such that  a.e. on
a.e. on  such that
such that

Consider the following assumptions.
(B1) The operator solution  is compact for
is compact for  .
.
(B2)There exist a function  and a continuous nondecreasing function
and a continuous nondecreasing function  such that
such that

with

(B3) For every  ,
,  is uniformly continuous.
is uniformly continuous.
In all the sequel we assume that  is exponentially bounded. Our first main existence result is the following.
is exponentially bounded. Our first main existence result is the following.
Theorem 4.3.
Assume  is a Carathéodory map satisfying
is a Carathéodory map satisfying 
 or
or  . Then problem (1.1) has at least one solution. If further
. Then problem (1.1) has at least one solution. If further  is a reflexive space, then the solution set is compact in
is a reflexive space, then the solution set is compact in  .
.
The following so-called nonlinear alternatives of Leray-Schauder type will be needed in the proof (see [31, 44]).
Lemma 4.4.
Let  be a normed space and
be a normed space and  a compact, u.s.c. multivalued map. Then either one of the following conditions holds.
a compact, u.s.c. multivalued map. Then either one of the following conditions holds.
-
(a)
 has at least one fixed point,
has at least one fixed point, -
(b)
the set
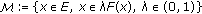 is unbounded.
is unbounded.
The single-valued version may be stated as follows.
Lemma 4.5.
Let  be a Banach space and
be a Banach space and  a nonempty bounded, closed, convex subset. Assume
a nonempty bounded, closed, convex subset. Assume  is an open subset of
is an open subset of  with
with  and let
and let  be a a continuous compact map. Then
be a a continuous compact map. Then
-
(a)
either there is a point
 and
and 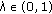 with
with 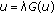 ,
, -
(b)
or
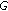 has a fixed point in
has a fixed point in 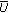 .
.
Proof of Theorem 4.3.
We have the following parts.
Part 1: Existence of Solutions
It is clear that all solutions of problem (1.1) are fixed points of the multivalued operator  defined by
defined by

where

Notice that the set  is nonempty (see Remark 2.12,(b)). Since, for each
is nonempty (see Remark 2.12,(b)). Since, for each  , the nonlinearity
, the nonlinearity  takes convex values, the selection set
takes convex values, the selection set  is convex and therefore
is convex and therefore  has convex values.
has convex values.
Step 1 ( is completely continuous). (a)
is completely continuous). (a)  sends bounded sets into bounded sets in
sends bounded sets into bounded sets in . Let
. Let  ,
,  be a bounded set in
be a bounded set in  , and
, and  . Then for each
. Then for each  , there exists
, there exists  such that
such that

Thus for each  ,
,

(b)  maps bounded sets into equicontinuous sets of
maps bounded sets into equicontinuous sets of . Let
. Let  ,
,  and
and  be a bounded set of
be a bounded set of  as in (a). Let
as in (a). Let  ; then for each
; then for each 

The right-hand side tends to zero as  since
since  is uniformly continuous.
is uniformly continuous.
(c) As a consequence of parts (a) and (b) together with the Arzéla-Ascoli theorem, it suffices to show that  maps
maps  into a precompact set in
into a precompact set in  . Let
. Let  and let
and let  . For
. For  , define
, define

Then

which tends to 0 as  . Therefore, there are precompact sets arbitrarily close to the set
. Therefore, there are precompact sets arbitrarily close to the set  . This set is then precompact in
. This set is then precompact in  .
.
Step 2 ( has a closed graph).
has a closed graph).
Let  and
and . We will prove that
. We will prove that  .
.  means that there exists
means that there exists  such that for each
such that for each 

First, we have

Now, consider the linear continuous operator  defined by
defined by

From the definition of  , we know that
, we know that

Since  and
and  is a closed graph operator by Lemma 2.13, then there exists
is a closed graph operator by Lemma 2.13, then there exists  such that
such that

Hence  , proving our claim. Lemma 2.10 implies that
, proving our claim. Lemma 2.10 implies that  is u.s.c.
is u.s.c.
Step 3 (a priori bounds on solutions).
Let  be such that
be such that  . Then there exists
. Then there exists  such that
such that

Then

Set

then  and for a.e.
and for a.e.  we have
we have

Thus

Using a change of variable we get

From  ) there exists
) there exists  such that
such that

Let

and consider the operator  . From the choice of
. From the choice of  , there is no
, there is no  such that
such that  for some
for some  . As a consequence of the Leray-Schauder nonlinear alternative (Lemma 4.4), we deduce that
. As a consequence of the Leray-Schauder nonlinear alternative (Lemma 4.4), we deduce that  has a fixed point
has a fixed point  in
in  which is a mild solution of problem (1.1).
which is a mild solution of problem (1.1).
Part 2: Compactness of the Solution Set
Let

From Part 1,  and there exists
and there exists  such that for every
such that for every  ,
,  . Since
. Since  is completely continuous, then
is completely continuous, then  is relatively compact in
is relatively compact in  . Let
. Let  ; then
; then  and
and  . It remains to prove that
. It remains to prove that  is closed set in
is closed set in  . Let
. Let  such that
such that  converge to
converge to  . For every
. For every  , there exists
, there exists  a.e.
a.e.  such that
such that

 implies that
implies that  , hence
, hence  is integrably bounded. Note this still remains true when
is integrably bounded. Note this still remains true when  holds for
holds for  is a bounded set. Since
is a bounded set. Since  is reflexive,
is reflexive,  is semicompact. By Lemma 2.15, there exists a subsequence, still denoted
is semicompact. By Lemma 2.15, there exists a subsequence, still denoted  , which converges weakly to some limit
, which converges weakly to some limit  . Moreover, the mapping
. Moreover, the mapping  defined by
defined by

is a continuous linear operator. Then it remains continuous if these spaces are endowed with their weak topologies. Therefore for a.e.  , the sequence
, the sequence  converges to
converges to  , it follows that
, it follows that

It remains to prove that  , for a.e.
, for a.e. . Lemma 2.16 yields the existence of
. Lemma 2.16 yields the existence of  ,
,  such that
such that  and the sequence of convex combinaisons
and the sequence of convex combinaisons  converges strongly to
converges strongly to  in
in  . Since
. Since  takes convex values, using Lemma 2.2, we obtain that
takes convex values, using Lemma 2.2, we obtain that

Since  is u.s.c. with compact values, then by Lemma 2.1, we have
is u.s.c. with compact values, then by Lemma 2.1, we have

This with (4.33) imply that  . Since
. Since  has closed, convex values, we deduce that
has closed, convex values, we deduce that  , for a.e.
, for a.e. , as claimed. Hence
, as claimed. Hence  which yields that
which yields that  is closed, hence compact in
is closed, hence compact in  .
.
4.2. The Convex Case: An MNC Approach
First, we gather together some material on the measure of noncompactness. For more details, we refer the reader to [36, 45] and the references therein.
Definition 4.6.
Let  be a Banach space and
be a Banach space and  a partially ordered set. A map
a partially ordered set. A map  is called a measure of noncompactness on
is called a measure of noncompactness on  , MNC for short, if
, MNC for short, if

for every  .
.
Notice that if  is dense in
is dense in  , then
, then  and hence
and hence

Definition 4.7.
A measure of noncompactness  is called
is called
-
(a)
monotone if
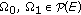 ,
,  implies
implies 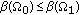 .
. -
(b)
nonsingular if
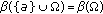 for every
for every  .
. -
(c)
invariant with respect to the union with compact sets if
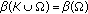 for every relatively compact set
for every relatively compact set  , and
, and 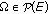 .
. -
(d)
real if
 and
and 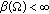 for every bounded
for every bounded  .
. -
(e)
semiadditive if
 for every
for every  .
. -
(f)
regular if the condition
 is equivalent to the relative compactness of
is equivalent to the relative compactness of  .
.
As example of an MNC, one may consider the Hausdorf MNC

Recall that a bounded set  has a finite
has a finite  -net if there exits a finite subset
-net if there exits a finite subset  such that
such that  where
where  is a closed ball in
is a closed ball in  .
.
Other examples are given by the following measures of noncompactness defined on the space of continuous functions  with values in a Banach space
with values in a Banach space  :
:
-
(i)
the modulus of fiber noncompactness
 (4.38)
(4.38)where
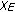 is the Hausdorff MNC in
is the Hausdorff MNC in  and
and  ;
; -
(ii)
the modulus of equicontinuity
 (4.39)
(4.39)It should be mentioned that these MNC satisfy all above-mentioned properties except regularity.
Definition 4.8.
Let M be a closed subset of a Banach space  and
and  an MNC on
an MNC on  . A multivalued map
. A multivalued map  is said to be
is said to be  -condensing if for every
-condensing if for every  , the relation
, the relation

implies the relative compactness of  .
.
Some important results on fixed point theory with MNCs are recalled hereafter (see, e.g., [36] for the proofs and further details). The first one is a compactness criterion.
Lemma 4.9 (see [36, Theorem 5.1.1]).
Let  be an abstract operator satisfying the following conditions:
be an abstract operator satisfying the following conditions:
(S1) is
is  -Lipschitz: there exists
-Lipschitz: there exists  such that for every
such that for every 

(S2) is weakly-strongly sequentially continuous on compact subsets: for any compact
is weakly-strongly sequentially continuous on compact subsets: for any compact  and any sequence
and any sequence  such that
such that  for a.e.
for a.e.  , the weak convergence
, the weak convergence  implies the strong convergence
implies the strong convergence  as
as  .
.
Then for every semicompact sequence  , the image sequence
, the image sequence  is relatively compact in
is relatively compact in  .
.
Lemma 4.10 (see [36, Theorem 5.2.2]).
Let an operator  satisfy conditions
satisfy conditions  together with the following:
together with the following:
(S3) there exits  such that for every integrable bounded sequence
such that for every integrable bounded sequence  , one has
, one has

where  is the Hausdorff MNC.
is the Hausdorff MNC.
Then

where  is the constant in
is the constant in  .
.
The next result is concerned with the nonlinear alternative for  -condensing u.s.c. multivalued maps.
-condensing u.s.c. multivalued maps.
Lemma 4.11 (see [36]).
Let  be a bounded open neighborhood of zero and
be a bounded open neighborhood of zero and  a
a  -condensing u.s.c. multivalued map, where
-condensing u.s.c. multivalued map, where  is a nonsingular measure of noncompactness defined on subsets of
is a nonsingular measure of noncompactness defined on subsets of  , satisfying the boundary condition
, satisfying the boundary condition

for all  and
and  . Then
. Then  .
.
Lemma 4.12 (see [36]).
Let  be a closed subset of a Banach space
be a closed subset of a Banach space  and
and  is a closed
is a closed  -condensing multivalued map where
-condensing multivalued map where  is a monotone MNC on
is a monotone MNC on  . If the fixed point set Fix
. If the fixed point set Fix  is bounded, then it is compact.
is bounded, then it is compact.
4.2.1. Main Results
In all this part, we assume that there exists  such that
such that

Let  be a Carathéodory multivalued map which satisfies Lipschitz conditions with respect to the Hausdorf MNC.
be a Carathéodory multivalued map which satisfies Lipschitz conditions with respect to the Hausdorf MNC.
(B4) There exists  such that for every bounded
such that for every bounded  in
in  ,
,

Lemma 4.13.
Under conditions  and
and  , the operator
, the operator  is closed and
is closed and  , for every
, for every  where
where  is as defined in the proof of Theorem 4.3.
is as defined in the proof of Theorem 4.3.
Proof.
We have the following steps.
Step 1 ( is closed).
is closed).
Let  , and
, and . We will prove that
. We will prove that  .
.  means that there exists
means that there exists  such that for a.e.
such that for a.e. 

Since  , Assumption
, Assumption  implies that
implies that  is integrably bounded. In addition, the set
is integrably bounded. In addition, the set  is relatively compact for a.e.
is relatively compact for a.e.  because Assumption
because Assumption  both with the convergence of
both with the convergence of  imply that
imply that

Hence the sequence  is semicompact, hence weakly compact in
is semicompact, hence weakly compact in  to some limit
to some limit  by Lemma 2.15. Arguing as in the proof of Theorem 4.3 Part 2, and passing to the limit in (4.47), we obtain that
by Lemma 2.15. Arguing as in the proof of Theorem 4.3 Part 2, and passing to the limit in (4.47), we obtain that  and for each
and for each 

As a consequence,  , as claimed.
, as claimed.
Step 2 ( has compact, convex values).
has compact, convex values).
The convexity of  follows immediately by the convexity of the values of
follows immediately by the convexity of the values of  . To prove the compactness of the values of
. To prove the compactness of the values of  , let
, let  for some
for some  and
and  . Then there exists
. Then there exists  satisfying (4.47). Arguing again as in Step 1, we prove that
satisfying (4.47). Arguing again as in Step 1, we prove that  is semicompact and converges weakly to some limit
is semicompact and converges weakly to some limit  , a.e.
, a.e. hence passing to the limit in (4.47),
hence passing to the limit in (4.47),  tends to some limit
tends to some limit  in the closed set
in the closed set  with
with  satisfying (4.49). Therefore the set
satisfying (4.49). Therefore the set  is sequentially compact, hence compact.
is sequentially compact, hence compact.
Lemma 4.14.
Under the conditions  and
and  , the operator
, the operator  is u.s.c.
is u.s.c.
Proof.
Using Lemmas 2.10 and 4.13, we only prove that  is quasicompact. Let
is quasicompact. Let  be a compact set in
be a compact set in  and
and  such that
such that  . Then there exists
. Then there exists  such that
such that

Since  is compact, we may pass to a subsequence, if necessary, to get that
is compact, we may pass to a subsequence, if necessary, to get that  converges to some limit
converges to some limit  in
in  . Arguing as in the proof of Theorem 4.3 Step 1, we can prove the existence of a subsequence
. Arguing as in the proof of Theorem 4.3 Step 1, we can prove the existence of a subsequence  which converges weakly to some limit
which converges weakly to some limit  and hence
and hence  converges to
converges to  , where
, where

As a consequence,  is u.s.c.
is u.s.c.
We are now in position to prove our second existence result in the convex case.
Theorem 4.15.
Assume that  satisfies Assumptions
satisfies Assumptions  and
and  . If
. If

then the set of solutions for problem (1.1) is nonempty and compact.
Proof.
It is clear that all solutions of problem (1.1) are fixed points of the multivalued operator  defined in Theorem 4.3. By Lemmas 4.13 and 4.14,
defined in Theorem 4.3. By Lemmas 4.13 and 4.14,  and it is u.s.c. Next, we prove that
and it is u.s.c. Next, we prove that  is a
is a  -condensing operator for a suitable MNC
-condensing operator for a suitable MNC  . Given a bounded subset
. Given a bounded subset  , let
, let  the modulus of quasiequicontinuity of the set of functions
the modulus of quasiequicontinuity of the set of functions  denote
denote

It is well known (see, e.g., [36, Example 2.1.2]) that  defines an MNC in
defines an MNC in  which satisfies all of the properties in Definition 4.7 except regularity. Given the Hausdorff MNC
which satisfies all of the properties in Definition 4.7 except regularity. Given the Hausdorff MNC  , let
, let  be the real MNC defined on bounded subsets on
be the real MNC defined on bounded subsets on  by
by

Finally, define the following MNC on bounded subsets of  by
by

where  is the collection of all countable subsets of
is the collection of all countable subsets of  . Then the MNC
. Then the MNC  is monotone, regular and nonsingular (see [36, Example 2.1.4]).
is monotone, regular and nonsingular (see [36, Example 2.1.4]).
To show that  is
is  -condensing, let
-condensing, let  be a bounded set in
be a bounded set in  such that
such that

We will show that  is relatively compact. Let
is relatively compact. Let  and let
and let  where
where  is defined by
is defined by

 is defined by
is defined by

Then

Moreover, each element  in
in  can be represented as
can be represented as

Moreover (4.56) yields

From Assumption  , it holds that for a.e.
, it holds that for a.e.  ,
,

Lemmas 4.9 and 4.10 imply that

Therefore

Since  , we infer that
, we infer that

 implies that
implies that  , for a.e.
, for a.e.  . In turn, (4.62) implies that
. In turn, (4.62) implies that

Hence (4.60) implies that  . To show that
. To show that  , i.e, the set
, i.e, the set  is equicontinuous, we proceed as in the proof of Theorem 4.3 Step 1 Part (b). It follows that
is equicontinuous, we proceed as in the proof of Theorem 4.3 Step 1 Part (b). It follows that  which implies, by (4.61), that
which implies, by (4.61), that  . We have proved that
. We have proved that  is relatively compact. Hence
is relatively compact. Hence  is u.s.c. and
is u.s.c. and  -condensing, where
-condensing, where  is as in the proof of Theorem 4.3. From the choice of
is as in the proof of Theorem 4.3. From the choice of  , there is no
, there is no  such that
such that  for some
for some  . As a consequence of the nonlinear alternative of Leray-Schauder type for condensing maps (Lemma 4.11), we deduce that
. As a consequence of the nonlinear alternative of Leray-Schauder type for condensing maps (Lemma 4.11), we deduce that  has a fixed point
has a fixed point  in
in  , which is a solution to problem (1.1). Finally, since
, which is a solution to problem (1.1). Finally, since  is bounded, by Lemma 4.12,
is bounded, by Lemma 4.12,  is further compact.
is further compact.
4.3. The Nonconvex Case
In this section, we present a second existence result for problem (1.1) when the multivalued nonlinearity is not necessarily convex. In the proof, we will make use of the nonlinear alternative of Leray-Schauder type [44] combined with a selection theorem due to Bressan and Colombo [46] for lower semicontinuous multivalued maps with decomposable values. The main ingredients are presented hereafter. We first start with some definitions (see, e.g., [47]). Consider a topological space  and a family
and a family  of subsets of
of subsets of  .
.
Definition 4.16.
 is called
is called  measurable if
measurable if  belongs to the
belongs to the  -algebra generated by all sets of the form
-algebra generated by all sets of the form  where
where  is Lebesgue measurable in
is Lebesgue measurable in  and
and  is Borel measurable in
is Borel measurable in  .
.
Definition 4.17.
A subset  is decomposable if for all
is decomposable if for all  and for every Lebesgue measurable set
and for every Lebesgue measurable set  , we have:
, we have:

where  stands for the characteristic function of the set
stands for the characteristic function of the set  .
.
Let  be a multivalued map with nonempty closed values. Assign to
be a multivalued map with nonempty closed values. Assign to  the multivalued operator
the multivalued operator  defined by
defined by  . The operator
. The operator  is called the Nemyts'kiĭ operator associated to
is called the Nemyts'kiĭ operator associated to  .
.
Definition 4.18.
Let  be a multivalued map with nonempty compact values. We say that
be a multivalued map with nonempty compact values. We say that  is of lower semicontinuous type (l.s.c. type) if its associated Nemyts'kiĭ operator
is of lower semicontinuous type (l.s.c. type) if its associated Nemyts'kiĭ operator  is lower semicontinuous and has nonempty closed and decomposable values.
is lower semicontinuous and has nonempty closed and decomposable values.
Next, we state a classical selection theorem due to Bressan and Colombo.
Let  be a separable metric space and let
be a separable metric space and let  be a Banach space. Then every l.s.c. multivalued operator
be a Banach space. Then every l.s.c. multivalued operator  ,
, with closed decomposable values has a continuous selection, that is, there exists a continuous single-valued function
with closed decomposable values has a continuous selection, that is, there exists a continuous single-valued function  such that
such that  for every
for every  .
.
Let us introduce the following hypothesis.
(H1)  is a nonempty compact valued multivalued map such that
is a nonempty compact valued multivalued map such that
-
(a)
the mapping
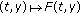 is
is  measurable;
measurable; -
(b)
the mapping
 is lower semicontinuous for a.e.
is lower semicontinuous for a.e. 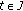 .
.
The following lemma is crucial in the proof of our existence theorem.
Lemma 4.20 (see, e.g., [48]).
Let  be an integrably bounded multivalued map satisfying
be an integrably bounded multivalued map satisfying  . Then
. Then  is of lower semicontinuous type.
is of lower semicontinuous type.
Theorem 4.21.
Suppose that the hypotheses  or
or  and
and  are satisfied. Then problem (1.1) has at least one solution.
are satisfied. Then problem (1.1) has at least one solution.
Proof.
 imply, by Lemma 4.20, that
imply, by Lemma 4.20, that  is of lower semicontinuous type. From Lemma 4.19, there is a continuous selection
is of lower semicontinuous type. From Lemma 4.19, there is a continuous selection  such that
such that  for all
for all  . Consider the problem
. Consider the problem

and the operator  defined by
defined by

As in Theorem 4.3, we can prove that the single-valued operator  is compact and there exists
is compact and there exists  such that for all possible solutions
such that for all possible solutions  , we have
, we have  . Now, we only check that
. Now, we only check that  is continuous. Let
is continuous. Let  be a sequence such that
be a sequence such that  in
in  , as
, as  . Then
. Then

Since the function  is continuous, we have
is continuous, we have

Let

From the choice of  , there is no
, there is no  such that
such that  for in
for in  . As a consequence of the nonlinear alternative of the Leray-Schauder type (Lemma 4.5), we deduce that
. As a consequence of the nonlinear alternative of the Leray-Schauder type (Lemma 4.5), we deduce that  has a fixed point
has a fixed point  which is a solution of problem (4.68), hence a solution to the problem (1.1).
which is a solution of problem (4.68), hence a solution to the problem (1.1).
4.4. A Further Result
In this part, we present a second existence result to problem (1.1) with a nonconvex valued right-hand side. First, consider the Hausdorff pseudo-metric distance

defined by

where  and
and  . Then
. Then  is a metric space and
is a metric space and  is a generalized metric space (see [49]). In particular,
is a generalized metric space (see [49]). In particular,  satisfies the triangle inequality.
satisfies the triangle inequality.
Definition 4.22.
A multivalued operator  is called
is called
-
(a)
 -Lipschitz if there exists
-Lipschitz if there exists 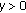 such that
such that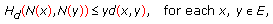 (4.75)
(4.75) -
(b)
a contraction if it is
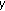 -Lipschitz with
-Lipschitz with  .
.
Notice that if  is
is  -Lipschitz, then for every
-Lipschitz, then for every  ,
,

Our proofs are based on the following classical fixed point theorem for contraction multivalued operators proved by Covitz and Nadler in 1970 [50] (see also Deimling [33, Theorem 11.1]).
Lemma 4.23.
Let  be a complete metric space. If
be a complete metric space. If  is a contraction, then
is a contraction, then  .
.
Let us introduce the following hypotheses:
(A1)  ;
;  is measurable for each
is measurable for each  ;
;
(A2) there exists a function  such that
such that

with

Theorem 4.24.
Let Assumptions  be satisfied. Then problem (1.1) has at least one solution.
be satisfied. Then problem (1.1) has at least one solution.
Proof.
In order to transform the problem (1.1) into a fixed point problem, let the multivalued operator  be as defined in Theorem 4.3. We will show that
be as defined in Theorem 4.3. We will show that  satisfies the assumptions of Lemma 4.23.
satisfies the assumptions of Lemma 4.23.
-
(a)
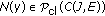 for each
for each 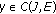 . Indeed, let
. Indeed, let  be a sequence converge to
be a sequence converge to  . Then there exists a sequence
. Then there exists a sequence  such that
such that  (4.79)
(4.79)
Since  has compact values, let
has compact values, let  be such that
be such that  . From
. From  and
and  , we infer that for a.e.
, we infer that for a.e. 

Then the Lebesgue dominated convergence theorem implies that, as  ,
,

with

proving that  .
.
(b) There exists  , such that
, such that

Let  and
and  . Then there exists
. Then there exists  (
( is a measurable selection) such that for each
is a measurable selection) such that for each 

( ) tells us that
) tells us that

Hence there is  such that
such that

Then consider the mapping  , given by
, given by

that is  . Since
. Since  are measurable, Theorem III.4.1 in [30] tells us that the closed ball
are measurable, Theorem III.4.1 in [30] tells us that the closed ball  is measurable. Finally the set
is measurable. Finally the set  is nonempty since it contains
is nonempty since it contains  . Therefore the intersection multivalued operator
. Therefore the intersection multivalued operator  is measurable with nonempty, closed values (see [29–31]). By Lemma 2.5, there exists a function
is measurable with nonempty, closed values (see [29–31]). By Lemma 2.5, there exists a function  , which is a measurable selection for
, which is a measurable selection for  . Thus
. Thus  and
and

Let us define for a.e. 

Then

Thus

By an analogous relation, obtained by interchanging the roles of  and
and  , we finally arrive at
, we finally arrive at

where  and
and

is the Bielecki-type norm on  . So,
. So,  is a contraction and thus, by Lemma 4.23,
is a contraction and thus, by Lemma 4.23,  has a fixed point
has a fixed point  , which is a mild solution to (1.1).
, which is a mild solution to (1.1).
Arguing as in Theorem 4.3, we can also prove the following result the proof of which is omitted.
Theorem 4.25.
Let  be a reflexive Banach space. Suppose that all conditions of Theorem 4.24 are satisfied and
be a reflexive Banach space. Suppose that all conditions of Theorem 4.24 are satisfied and  . Then the solution set of problem (1.1) is nonempty and compact.
. Then the solution set of problem (1.1) is nonempty and compact.
5. Filippov's Theorem
5.1. Filippov's Theorem on a Bounded Interval
Let  be a mild solution of the integral equation:
be a mild solution of the integral equation:

We will consider the following two assumptions.
(C1)The function  is such that
is such that
-
(a)
for all
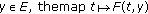 is measurable,
is measurable, -
(b)
the map
 is integrable.
is integrable.
(C2)There exist a function  and a positive constant
and a positive constant  such that
such that

Theorem 5.1.
Assume that the conditions  . Then, for every
. Then, for every  problem (1.1) has at least one solution
problem (1.1) has at least one solution  satisfying, for a.e.
satisfying, for a.e.  , the estimates
, the estimates

where  .
.
Proof.
We construct a sequence of functions  which will be shown to converge to some solution of problem (1.1) on the interval
which will be shown to converge to some solution of problem (1.1) on the interval  , namely, to
, namely, to

Let  on
on  and
and  , that is,
, that is,

Then define the multivalued map  by
by  . Since
. Since  and
and  are measurable, Theorem III.4.1 in [30] tells us that the ball
are measurable, Theorem III.4.1 in [30] tells us that the ball  is measurable. Moreover
is measurable. Moreover  is measurable (see [29]) and
is measurable (see [29]) and  is nonempty. Indeed, since
is nonempty. Indeed, since  is a measurable function, from Lemma 2.6, there exists a function
is a measurable function, from Lemma 2.6, there exists a function  which is a measurable selection of
which is a measurable selection of  and such that
and such that

Then  , proving our claim. We deduce that the intersection multivalued operator
, proving our claim. We deduce that the intersection multivalued operator  is measurable (see [29–31]). By Lemma 2.7 (Kuratowski-Ryll-Nardzewski selection theorem), there exists a function
is measurable (see [29–31]). By Lemma 2.7 (Kuratowski-Ryll-Nardzewski selection theorem), there exists a function  which is a measurable selection for
which is a measurable selection for  . Consider
. Consider

For each  , we have
, we have

Hence

Using the fact that  is measurable, the ball
is measurable, the ball  is also measurable by Theorm III.4.1 in [30]. From
is also measurable by Theorm III.4.1 in [30]. From  we have
we have

Hence there exist  such that
such that

We consider the following multivalued map  is nonempty. Therefore the intersection multivalued operator
is nonempty. Therefore the intersection multivalued operator  is measurable with nonempty, closed values (see [29–31]). By Lemma 2.5, there exists a function
is measurable with nonempty, closed values (see [29–31]). By Lemma 2.5, there exists a function  , which is a measurable selection for
, which is a measurable selection for  . Thus
. Thus  and
and

Define

Using (5.8) and (5.12), a simple integration by parts yields the following estimates, valid for every  :
:

Let  . Arguing as for
. Arguing as for  , we can prove that
, we can prove that  is a measurable multivalued map with nonempty values; so there exists a measurable selection
is a measurable multivalued map with nonempty values; so there exists a measurable selection  . This allows us to define
. This allows us to define

For  , we have
, we have

Then

Performing an integration by parts, we obtain, since  is a nondecreasing function, the following estimates:
is a nondecreasing function, the following estimates:

Let  . Then, arguing again as for
. Then, arguing again as for  ,
,  ,
,  , we show that
, we show that  is a measurable multivalued map with nonempty values and that there exists a measurable selection
is a measurable multivalued map with nonempty values and that there exists a measurable selection  in
in  . Define
. Define

For  , we have
, we have

Repeating the process for  , we arrive at the following bound:
, we arrive at the following bound:

By induction, suppose that (5.21) holds for some  and check (5.21) for
and check (5.21) for  . Let
. Let  . Since
. Since  is a nonempty measurable set, there exists a measurable selection
is a nonempty measurable set, there exists a measurable selection  , which allows us to define for
, which allows us to define for 

Therefore, for a.e.  , we have
, we have

Again, an integration by parts leads to

Consequently, (5.21) holds true for all  . We infer that
. We infer that  is a Cauchy sequence in
is a Cauchy sequence in  , converging uniformly to a limit function
, converging uniformly to a limit function  . Moreover, from the definition of
. Moreover, from the definition of  , we have
, we have

Hence, for a.e.  ,
,  is also a Cauchy sequence in
is also a Cauchy sequence in  and then converges almost everywhere to some measurable function
and then converges almost everywhere to some measurable function  in
in  . In addition, since
. In addition, since  , we have for a.e.
, we have for a.e. 

Hence

where

From the Lebesgue dominated convergence theorem, we deduce that  converges to
converges to  in
in  . Passing to the limit in (5.22), we find that the function
. Passing to the limit in (5.22), we find that the function

is solution to problem (1.1) on  . Moreover, for a.e.
. Moreover, for a.e.  , we have
, we have

Passing to the limit as  , we get
, we get

with

6. The Relaxed Problem
More precisely, we compare, in this section, trajectories of the following problem,

and those of the convexified Volttera integral inclusion problem

where  refers to the closure of the convex hull of the set
refers to the closure of the convex hull of the set  . We will need the following auxiliary results in order to prove our main relaxation theorem.
. We will need the following auxiliary results in order to prove our main relaxation theorem.
Lemma 6.1 (see [29]).
Let  be a measurable, integrably bounded set-valued map and let
be a measurable, integrably bounded set-valued map and let  be an integrable map. Then the integral
be an integrable map. Then the integral  is convex, the map
is convex, the map  is measurable and, for every
is measurable and, for every  , and every measurable selection
, and every measurable selection  of
of  , there exists a measurable selection
, there exists a measurable selection  of
of  such that
such that

With  being a reflexive Banach space, the following hypotheses will be assumed in this section:
being a reflexive Banach space, the following hypotheses will be assumed in this section:
The function  satisfies
satisfies
(a)for all  the map
the map  is measurable,
is measurable,
(b)the map  is integrable bounded (i.e., there exists
is integrable bounded (i.e., there exists  such that
such that  .
.
Then our main contribution is the following.
Theorem 6.2.
Assume that  and
and  hold. Then problem (6.2) has at least one solution. In addition, for all
hold. Then problem (6.2) has at least one solution. In addition, for all  and every solution
and every solution  of problem (6.2), has a solution
of problem (6.2), has a solution  defined on
defined on  satisfying
satisfying

In particular  , where
, where

Remark 6.3.
Notice that the multivalued map  also satisfies
also satisfies  .
.
Proof.
Part 1 ( )
)
For this, we first transform problem (6.2) into a fixed point problem and then make use of Lemma 4.23. It is clear that all solutions of problem (6.2) are fixed points of the multivalued operator  defined by
defined by

where

To show that  satisfies the assumptions of Lemma 4.23, the proof will be given in two steps.
satisfies the assumptions of Lemma 4.23, the proof will be given in two steps.
Step 1.
 for each
for each  . Indeed, let
. Indeed, let  be such that
be such that  in
in  , as
, as  . Then
. Then  and there exists a sequence
and there exists a sequence  such that
such that

Then  is integrably bounded. Since
is integrably bounded. Since  has closed values and integrable bounded, then from Corollary 4.14 for every
has closed values and integrable bounded, then from Corollary 4.14 for every  we have
we have  such that
such that

Since  is a convergent sequence the there exists
is a convergent sequence the there exists  such that
such that

Then

that is

Since  is weakly compact in the reflexive Banach space
is weakly compact in the reflexive Banach space  , there exists a subsequence, still denoted
, there exists a subsequence, still denoted  , which converges weakly to
, which converges weakly to  by the Dunford-Pettis theorem. By Mazur's Lemma (Lemma 2.16), there exists a second subsequence which converges strongly to
by the Dunford-Pettis theorem. By Mazur's Lemma (Lemma 2.16), there exists a second subsequence which converges strongly to  in
in  , hence almost everywhere. Then the Lebesgue dominated convergence theorem implies that, as
, hence almost everywhere. Then the Lebesgue dominated convergence theorem implies that, as  ,
,

proving that  .
.
Step 2.
There exists  such that
such that  for each
for each  where the norm
where the norm  will be chosen conveniently. Indeed, let
will be chosen conveniently. Indeed, let  and
and  . Then there exists
. Then there exists  such that for each
such that for each 

Since, for each  ,
,

then there exists some  such that
such that

Consider the multimap  defined by
defined by

As in the proof of Theorem 5.1, we can show that the multivalued operator  is measurable and takes nonempty values. Then there exists a function
is measurable and takes nonempty values. Then there exists a function  , which is a measurable selection for
, which is a measurable selection for  . Thus,
. Thus,  and
and

For each  , let
, let

Therefore, for each  , we have
, we have

Hence

where

By an analogous relation, obtained by interchanging the roles of  and
and  , we find that
, we find that

Then  is a contraction and hence, by Lemma 4.23,
is a contraction and hence, by Lemma 4.23,  has a fixed point
has a fixed point  , which is solution to problem (6.2).
, which is solution to problem (6.2).
Part 2
Let  be a solution of problem (6.2). Then, there exists
be a solution of problem (6.2). Then, there exists  such that
such that

that is,  is a solution of the problem
is a solution of the problem

Let  and
and  be given by the relation
be given by the relation  . From Lemma 6.1, there exists a measurable selection
. From Lemma 6.1, there exists a measurable selection  of
of  such that
such that

Let

Hence

With Assumption  , we infer from Corollary 4.14 that there exists
, we infer from Corollary 4.14 that there exists  such that
such that

Then

Since, under  and
and  ,
,  is measurable (see [29]), by the above inequality, we deduce that
is measurable (see [29]), by the above inequality, we deduce that  . From Theorem 5.1, problem (6.1) has a solution
. From Theorem 5.1, problem (6.1) has a solution  which satisfies
which satisfies

where

Using the definition of  , we obtain the upper bound
, we obtain the upper bound

Since  is arbitrary,
is arbitrary,  , showing the density relation
, showing the density relation  .
.
References
Benchohra M, Henderson J, Ntouyas SK: The method of upper and lower solutions for an integral inclusion of Volterra type. Communications on Applied Nonlinear Analysis 2002,9(1):67-74.
Bulgakov AI, Ljapin LN: Some properties of the set of solutions of a Volterra-Hammerstein integral inclusion. Differential Equations 1978,14(8):1043-1048.
Corduneanu C: Integral Equations and Applications. Cambridge University Press, Cambridge, UK; 1991:x+366.
Gripenberg G, Londen S-O, Staffans O: Volterra Integral and Functional Equations, Encyclopedia of Mathematics and Its Applications. Volume 34. Cambridge University Press, Cambridge, UK; 1990:xxii+701.
Appell J, de Pascale E, Nguyêñ HT, Zabreĭko PP: Nonlinear integral inclusions of Hammerstein type. Topological Methods in Nonlinear Analysis 1995,5(1):111-124.
Benchohra M, Nieto JJ, Ouahabi A: Existence results for functional integral inclusions of Volterra type. Dynamic Systems and Applications 2005,14(1):57-69.
O'Regan D: Integral inclusions of upper semi-continuous or lower semi-continuous type. Proceedings of the American Mathematical Society 1996,124(8):2391-2399. 10.1090/S0002-9939-96-03456-9
Kannan R, O'Regan D: A note on the solution set of integral inclusions. Journal of Integral Equations and Applications 2000,12(1):85-94. 10.1216/jiea/1020282135
Prato D, Iannelli GM: Linear integrodifferential equations in Banach space. Rendiconti del Seminario Matematico della Università di Padova 1980, 62: 207-219.
Araya D, Lizama C: Almost automorphic mild solutions to fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3692-3705. 10.1016/j.na.2007.10.004
Bajlekova EG: Fractional evolution equations in Banach spaces, Ph.D. thesis. Eindhoven University of Technology, Eindhoven, UK; 2001.
Chen C, Li M: On fractional resolvent operator functions. Semigroup Forum 2010,80(1):121-142. 10.1007/s00233-009-9184-7
Clément P, Prüss J: Global existence for a semilinear parabolic Volterra equation. Mathematische Zeitschrift 1992,209(1):17-26. 10.1007/BF02570816
Cuevas C, Lizama C: Almost automorphic solutions to a class of semilinear fractional differential equations. Applied Mathematics Letters 2008,21(12):1315-1319. 10.1016/j.aml.2008.02.001
Henríquez HR, Lizama C: Compact almost automorphic solutions to integral equations with infinite delay. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):6029-6037. 10.1016/j.na.2009.05.042
Lizama C: Regularized solutions for abstract Volterra equations. Journal of Mathematical Analysis and Applications 2000,243(2):278-292. 10.1006/jmaa.1999.6668
Lizama C: On an extension of the Trotter-Kato theorem for resolvent families of operators. Journal of Integral Equations and Applications 1990,2(2):269-280. 10.1216/JIE-1990-2-2-263
Lizama C: A characterization of periodic resolvent operators. Results in Mathematics 1990,18(1-2):93-105.
Lizama C, Vergara V: Uniform stability of resolvent families. Proceedings of the American Mathematical Society 2004,132(1):175-181. 10.1090/S0002-9939-03-07073-4
Lizama C: On Volterra equations associated with a linear operator. Proceedings of the American Mathematical Society 1993,118(4):1159-1166. 10.1090/S0002-9939-1993-1152281-3
Lizama C, Poblete V: On multiplicative perturbation of integral resolvent families. Journal of Mathematical Analysis and Applications 2007,327(2):1335-1359. 10.1016/j.jmaa.2006.04.087
Lizama C, Sánchez J:On perturbation of
 -regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.
-regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.Oka H: Linear Volterra equations and integrated solution families. Semigroup Forum 1996,53(3):278-297. 10.1007/BF02574144
Prüss J: Evolutionary Integral Equations and Applications, Monographs in Mathematics. Volume 87. Birkhäuser, Basel, Switzerland; 1993:xxvi+366.
Agarwal RP, Benchohra M, Nieto JJ, Ouahab A: Fractional Differential Equations and Inclusions. Springer, Berlin, Germany;
Lakshmikantham V, Leela S, Vasundhara Devi J: Theory of Fractional Dynamic Systems. Cambridge Scientific Publishers, Cambridge, UK; 2009.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Yosida K: Functional Analysis, Grundlehren der Mathematischen Wissenschaften. Volume 123. 6th edition. Springer, Berlin, Germany; 1980:xii+501.
Aubin J-P, Frankowska H: Set-Valued Analysis, Systems & Control: Foundations & Applications. Volume 2. Birkhäuser Boston, Boston, Mass, USA; 1990:xx+461.
Castaing C, Valadier M: Convex Analysis and Measurable Multifunctions, Lecture Notes in Mathematics. Volume 580. Springer, Berlin, Germany; 1977:vii+278.
Górniewicz L: Topological Fixed Point Theory of Multi-Valued Mappings, Mathematics and Its Applications. Volume 495. Kluwer Academic Publishers, Dordrecht, Netherlands; 1999.
Zhu QJ: On the solution set of differential inclusions in Banach space. Journal of Differential Equations 1991,93(2):213-237. 10.1016/0022-0396(91)90011-W
Deimling K: Multi-Valued Differential Equations. De Gruyter, Berlin, Germany; 1992.
Hu S, Papageorgiou NS: Handbook of Multivalued Analysis. Vol. I. Theory, Mathematics and Its Applications. Volume 419. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:xvi+964.
Lasota A, Opial Z: An application of the Kakutani—Ky Fan theorem in the theory of ordinary differential equations. Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques 1965, 13: 781-786.
Kamenskii M, Obukhovskii V, Zecca P: Condensing Multivalued Maps and Semilinear Differential Inclusions in Banach Spaces, de Gruyter Series in Nonlinear Analysis and Applications. Volume 7. Walter de Gruyter, Berlin, Germany; 2001:xii+231.
Andres J, Górniewicz L: Topological Fixed Point Principles for Boundary Value Problems. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003.
Aubin J-P, Cellina A: Differential Inclusions. Set-Valued Maps and Viability Theory, Grundlehren der Mathematischen Wissenschaften. Volume 264. Springer, Berlin, Germany; 1984:xiii+342.
Tolstonogov AA: Differential Inclusions in Banach Spaces. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000.
Arendt W, Batty CJK, Hieber M, Neubrander F: Vector-Valued Laplace Transforms and Cauchy Problems, Monographs in Mathematics. Volume 96. Birkhäuser, Basel, Switzerland; 2001:xii+523.
Engel K-J, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000:xxii+586.
Fattorini HO: Second Order Linear Differential Equations in Banach Spaces, North-Holland Mathematics Studies. Volume 108. North-Holland, Amsterdam, The Netherlands; 1985:xiii+314.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Granas A, Dugundji J: Fixed Point Theory, Springer Monographs in Mathematics. Springer, New York, NY, USA; 2003:xvi+690.
Ayerbe Toledano JM, Domínguez Benavides T, López Acedo G: Measures of Noncompactness in Metric Fixed Point Theory, Operator Theory: Advances and Applications. Volume 99. Birkhäuser, Basel, Switzerland; 1997:viii+211.
Bressan A, Colombo G: Extensions and selections of maps with decomposable values. Studia Mathematica 1988,90(1):69-86.
Fryszkowski AJ: Topological Fixed Point Theory and Its Applications. Kluwer Academic Publishers, Dordrecht, Netherlands; 2004.
Frigon M, Granas A: Théorèmes d'existence pour des inclusions différentielles sans convexité. Comptes Rendus de l'Académie des Sciences. Série I. Mathématique 1990,310(12):819-822.
Kisielewicz M: Differential Inclusions and Optimal Control, Mathematics and Its Applications (East European Series). Volume 44. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xx+240.
Covitz H, Nadler SB Jr.: Multi-valued contraction mappings in generalized metric spaces. Israel Journal of Mathematics 1970, 8: 5-11. 10.1007/BF02771543
Acknowledgments
This paper was completed when the second and forth authors visited the Department of Mathematical Analysis of the University of Santiago de Compostela. The authors would like to thank the department for its hospitality and support. The authors are grateful to the referee for carefully reading the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R.P., Benchohra, M., Nieto, J.J. et al. Some Results for Integral Inclusions of Volterra Type in Banach Spaces. Adv Differ Equ 2010, 798067 (2010). https://doi.org/10.1155/2010/798067
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/798067
 , the set
, the set 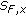 is closed whenever
is closed whenever  has closed values. It is convex if and only if
has closed values. It is convex if and only if 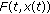 is convex for
is convex for  .
.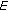 is finite-dimensional), we know that
is finite-dimensional), we know that  is nonempty if and only if the mapping
is nonempty if and only if the mapping  belongs to
belongs to 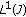 . It is bounded if and only if the mapping
. It is bounded if and only if the mapping  belongs to
belongs to  ; this particularly holds true when
; this particularly holds true when 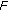 is
is 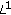 -Carathéodory. For the sake of completeness, we refer also to Theorem 1.3.5 in [
-Carathéodory. For the sake of completeness, we refer also to Theorem 1.3.5 in [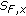 contains a measurable selection whenever
contains a measurable selection whenever  is measurable and
is measurable and  is a Carathéodory function.
is a Carathéodory function.
 such that
such that
 is relatively compact in
is relatively compact in 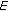 for a.e.
for a.e.  .
.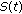 is strongly continuous for
is strongly continuous for  and
and  ;
; and
and 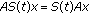 for all
for all  ;
;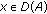 and
and 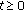 ,
,
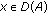 . Then
. Then  , and
, and
 has at least one fixed point,
has at least one fixed point,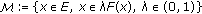 is unbounded.
is unbounded. and
and 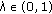 with
with 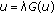 ,
,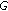 has a fixed point in
has a fixed point in 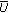 .
.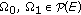 ,
,  implies
implies 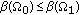 .
.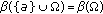 for every
for every  .
.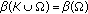 for every relatively compact set
for every relatively compact set  , and
, and 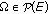 .
. and
and 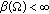 for every bounded
for every bounded  .
. for every
for every  .
. is equivalent to the relative compactness of
is equivalent to the relative compactness of  .
.
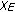 is the Hausdorff MNC in
is the Hausdorff MNC in  and
and  ;
;
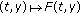 is
is  measurable;
measurable; is lower semicontinuous for a.e.
is lower semicontinuous for a.e. 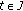 .
. -Lipschitz if there exists
-Lipschitz if there exists 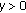 such that
such that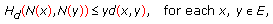
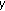 -Lipschitz with
-Lipschitz with  .
.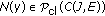 for each
for each  . Indeed, let
. Indeed, let  be a sequence converge to
be a sequence converge to  . Then there exists a sequence
. Then there exists a sequence  such that
such that 
 is measurable,
is measurable, is integrable.
is integrable. -regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.
-regularized resolvent families. Taiwanese Journal of Mathematics 2003,7(2):217-227.