- Research Article
- Open access
- Published:
Nonlinear Delay Discrete Inequalities and Their Applications to Volterra Type Difference Equations
Advances in Difference Equations volume 2010, Article number: 795145 (2010)
Abstract
Delay discrete inequalities with more than one nonlinear term are discussed, which generalize some known results and can be used in the analysis of various problems in the theory of certain classes of discrete equations. Application examples to show boundedness and uniqueness of solutions of a Volterra type difference equation are also given.
1. Introduction
Gronwall-Bellman inequalities and their various linear and nonlinear generalizations play very important roles in the discussion of existence, uniqueness, continuation, boundedness, and stability properties of solutions of differential equations and difference equations. The literature on such inequalities and their applications is vast. For example, see [1–12] for continuous cases, and [13–20] for discrete cases. In particular, the book [21] written by Pachpatte considered three types of discrete inequalities:

In this paper, we consider a delay discrete inequality

which has  nonlinear terms where
nonlinear terms where  . We will show that many discrete inequalities like (1.1) can be reduced to this form. Our main result can be applied to analyze properties of solutions of discrete equations. We also give examples to show boundedness and uniqueness of solutions of a Volterra type difference equation.
. We will show that many discrete inequalities like (1.1) can be reduced to this form. Our main result can be applied to analyze properties of solutions of discrete equations. We also give examples to show boundedness and uniqueness of solutions of a Volterra type difference equation.
2. Main Results
Assume that
-
(C1)
 is nonnegative for
is nonnegative for 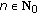 and
and 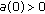 ;
; -
(C2)
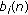
 are nondecreasing for
are nondecreasing for  , the range of each
, the range of each 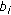 belongs to
belongs to  , and
, and 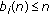 ;
; -
(C3) all

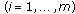 are nonnegative for
are nonnegative for 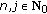 ;
; -
(C4) all
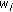
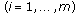 are continuous and nondecreasing functions on
are continuous and nondecreasing functions on  and are positive on
and are positive on 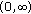 . They satisfy the relationship
. They satisfy the relationship  where
where 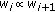 means that
means that 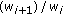 is nondecreasing on
is nondecreasing on  (see [10]).
(see [10]).
Let  for
for  where
where  is a given constant. Then,
is a given constant. Then,  is strictly increasing so its inverse
is strictly increasing so its inverse  is well defined, continuous, and increasing in its corresponding domain. Define
is well defined, continuous, and increasing in its corresponding domain. Define  ,
,  and
and  .
.
Theorem 2.1.
Suppose that ( )–(
)–( ) hold and
) hold and  is a nonnegative function for
is a nonnegative function for  satisfying (1.2). Then
satisfying (1.2). Then

where  ,
,  ,
,  is determined recursively by
is determined recursively by

 ,
,  ,
,  (Identity), and
(Identity), and  is the largest positive integer such that
is the largest positive integer such that

Remark 2.2.
-
(1)
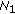 is defined by (2.3) and
is defined by (2.3) and 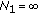 when all
when all 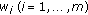 satisfy
satisfy  . Different choices of
. Different choices of  in
in  do not affect our results (see [2]).
do not affect our results (see [2]). -
(2)
If
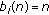 for
for 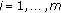 , then (2.1) gives the estimate of the following inequality:
, then (2.1) gives the estimate of the following inequality:

by replacing  ,
,  ,
,  ,
,  , and
, and  with
with  ,
,  ,
,  ,
,  and
and  , respectively. Especially, if
, respectively. Especially, if  and
and  , then (1.2) for
, then (1.2) for  becomes the first inequality of (1.1). Equation (2.1) shows the same estimate given by (
becomes the first inequality of (1.1). Equation (2.1) shows the same estimate given by ( ) of Theorem 4.2.3 in the book [21].
) of Theorem 4.2.3 in the book [21].
Lemma 2.3.
 is nonnegative and nondecreasing in
is nonnegative and nondecreasing in  , and
, and  is nonnegative and nondecreasing in
is nonnegative and nondecreasing in  and
and  for
for  .
.
Proof.
By the definitions of  and
and  , it is easy to check that they are nonnegative and nondecreasing in
, it is easy to check that they are nonnegative and nondecreasing in  , and
, and  and
and  for each fixed
for each fixed  where
where  .
.  in (
in ( ) implies that
) implies that  for all
for all  . Clearly,
. Clearly,

where  is used, which yields that
is used, which yields that  and
and  are nondecreasing in
are nondecreasing in  . Assume that
. Assume that  is nondecreasing in
is nondecreasing in  . Then
. Then

which implies that  is nondecreasing in
is nondecreasing in  . By induction,
. By induction, 
 are nondecreasing in
are nondecreasing in  . Similarly, we can prove that they are nonnegative by induction again. Then
. Similarly, we can prove that they are nonnegative by induction again. Then 
 are nonnegative and nondecreasing in
are nonnegative and nondecreasing in  and
and  .
.
Proof of Theorem 2.1.
Take any arbitrary positive integer  and consider the auxiliary inequality
and consider the auxiliary inequality

Claim that  in (2.7) satisfies
in (2.7) satisfies

for  where
where  is the largest positive integer such that
is the largest positive integer such that


Before we prove (2.8), notice that  . In fact,
. In fact,  ,
,  , and
, and  are nondecreasing in
are nondecreasing in  by Lemma 2.3. Thus,
by Lemma 2.3. Thus,  satisfying (2.9) gets smaller as
satisfying (2.9) gets smaller as  is chosen larger. In particular,
is chosen larger. In particular,  satisfies the same (2.3) as
satisfies the same (2.3) as  for
for  if
if  is applied.
is applied.
We divide the proof of (2.8) into two steps by using induction.
Step 1 ( ).
).
Let  for
for  and
and  . It is clear that
. It is clear that  is nonnegative and nondecreasing. Observe that (2.7) is equivalent to
is nonnegative and nondecreasing. Observe that (2.7) is equivalent to  for
for  and by assumptions (
and by assumptions ( ) and (
) and ( ) and Lemma 2.3,
) and Lemma 2.3,

Since  is nondecreasing and
is nondecreasing and  , we have
, we have

Then

and so

The definition of  in Theorem 2.1 and
in Theorem 2.1 and  show
show

Equation (2.9) shows that the right side of (2.14) is in the domain of  for all
for all  . Thus the monotonicity of
. Thus the monotonicity of  implies
implies

for  ; that is, (2.8) is true for
; that is, (2.8) is true for  .
.
Step 2 ( ).
).
Assume that (2.8) is true for  . Consider
. Consider

Let  and
and  . Then
. Then  is nonnegative and nondecreasing and satisfies
is nonnegative and nondecreasing and satisfies  for
for  . Moreover, we have
. Moreover, we have

Since  and
and  are nondecreasing in their arguments and
are nondecreasing in their arguments and  , we have by the assumption
, we have by the assumption 

for  where
where  for
for  , which gives
, which gives

Therefore,

that is,

or equivalently

the same as (2.7) for  where
where  and
and

From the assumption ( ), each
), each  ,
,  , is continuous and nondecreasing on
, is continuous and nondecreasing on  and is positive on
and is positive on  since
since  is continuous and nondecreasing on
is continuous and nondecreasing on  . Moreover,
. Moreover,  . By the inductive assumption, we have
. By the inductive assumption, we have

for  where
where  ,
,  ,
,  (Identity),
(Identity),  ,
,  is the inverse of
is the inverse of  ,
,  ,
,  ,
,

i and
and  is the largest positive integer such that
is the largest positive integer such that

Note that

Thus, we have from (2.24) that

for  since
since  .
.
In the following, we prove that  by induction again.
by induction again.
It is clear that  for
for  . Suppose that
. Suppose that  for
for  . We have
. We have

where  is applied. It implies that it is true for
is applied. It implies that it is true for  . Thus,
. Thus,  for
for  .
.
Equation (2.26) becomes

for  . It implies that
. It implies that  . Thus, (2.28) becomes
. Thus, (2.28) becomes

for  . It shows that (2.8) is true for
. It shows that (2.8) is true for  . Thus, the claim is proved.
. Thus, the claim is proved.
Now we prove (2.1). Replacing  by
by  in (2.8), we have
in (2.8), we have

Since (2.8) is true for any  , we replace
, we replace  by
by  and get
and get

This is exactly (2.1) since  . This proves Theorem 2.1.
. This proves Theorem 2.1.
Remark 2.4.
If  for all
for all  , then
, then  . Let
. Let  where
where  is given in
is given in  . Using the same arguments as in (2.11) where
. Using the same arguments as in (2.11) where  is replaced with the positive
is replaced with the positive  , we have
, we have  and (2.14) becomes
and (2.14) becomes

that is,

which is the same as (2.15) with a complementary definition that  . From (
. From ( ) of Remark 2.2, the estimate of (2.35) is independent of
) of Remark 2.2, the estimate of (2.35) is independent of  . Then we similarly obtain (2.1) and all
. Then we similarly obtain (2.1) and all  are defined by the same formula (2.2) where we define
are defined by the same formula (2.2) where we define  for
for  .
.
3. Some Corollaries
In this section, we apply Theorem 2.1 and obtain some corollaries.
Assume that  is a strictly increasing function with
is a strictly increasing function with  where
where  . Consider the inequality
. Consider the inequality

Corollary 3.1.
Suppose that  )–(
)–( ) hold. If
) hold. If in(3.1)is nonnegative for
in(3.1)is nonnegative for , then
, then

for  where
where  ,
,  is the inverse of
is the inverse of  ,
,  ,
,  ,
,  , and other related functions are defined as in Theorem 2.1 by replacing
, and other related functions are defined as in Theorem 2.1 by replacing  with
with  .
.
Proof.
Let  . Then (3.1) becomes
. Then (3.1) becomes

Note that  satisfy (
satisfy ( ) for
) for  . Using Theorem 2.1, we obtain the estimate about
. Using Theorem 2.1, we obtain the estimate about  by replacing
by replacing  with
with  . Then use the fact that
. Then use the fact that  and we get Corollary 3.1.
and we get Corollary 3.1.
If  where
where  , then (3.1) reads
, then (3.1) reads

Directly using Corollary 3.1, we have the following result.
Corollary 3.2.
Suppose that  )–(
)–( ) hold. If
) hold. If in (3.4) is nonnegative for
in (3.4) is nonnegative for , then
, then

for  where
where  ,
,  is the inverse of
is the inverse of  ,
,  ,
,  ,
,  , and other related functions are defined as in Theorem 2.1 by replacing
, and other related functions are defined as in Theorem 2.1 by replacing  with
with  .
.
If  ,
,  ,
,  , (3.4) becomes the second inequality of (1.1) with
, (3.4) becomes the second inequality of (1.1) with  and
and  , and the third inequality of (1.1) with
, and the third inequality of (1.1) with  and
and  , which are discussed in the book [21]. Equation (3.5) yields the same estimates of Theorem 4.2.4 in the book [21].
, which are discussed in the book [21]. Equation (3.5) yields the same estimates of Theorem 4.2.4 in the book [21].
4. Applications to Volterra Type Difference Equations
In this section, we apply Theorem 2.1 to study boundedness and uniqueness of solutions of a nonlinear delay difference equation of the form

where  is an unknown function,
is an unknown function,  maps from
maps from  to
to  ,
,  and
and  map from
map from  to
to  , and
, and  satisfies the assumption (
satisfies the assumption ( ) for
) for  .
.
Theorem.
Suppose that  and the functions
and the functions  and
and  in (4.1) satisfy the conditions
in (4.1) satisfy the conditions

where  . If
. If  is a solution of (4.1) on
is a solution of (4.1) on  , then
, then

where

Proof.
Using (4.1) and (4.2), the solution  satisfies
satisfies

where

Clearly,  for all
for all  since
since  . For positive constants
. For positive constants  , we have
, we have

It is obvious that  and
and  satisfy (
satisfy ( ). Applying Theorem 2.1 gives
). Applying Theorem 2.1 gives

which implies (4.3).
Theorem.
Suppose that  and the functions
and the functions  and
and  in (4.1) satisfy the conditions
in (4.1) satisfy the conditions

where  . Then (4.1) has at most one solution on
. Then (4.1) has at most one solution on  .
.
Proof.
Let  and
and  be two solutions of (4.1) on
be two solutions of (4.1) on  . From (4.9), we have
. From (4.9), we have

where  ,
,  ,
,  and
and  . Appling Theorem 2.1, Remark 2.4, and the notation
. Appling Theorem 2.1, Remark 2.4, and the notation  for
for  , we obtain that
, we obtain that  which implies that the solution is unique.
which implies that the solution is unique.
References
Agarwal RP:On an integral inequality in
 independent variables. Journal of Mathematical Analysis and Applications 1982,85(1):192-196. 10.1016/0022-247X(82)90034-8
independent variables. Journal of Mathematical Analysis and Applications 1982,85(1):192-196. 10.1016/0022-247X(82)90034-8Agarwal RP, Deng S, Zhang W: Generalization of a retarded Gronwall-like inequality and its applications. Applied Mathematics and Computation 2005,165(3):599-612. 10.1016/j.amc.2004.04.067
Bihari I: A generalization of a lemma of Bellman and its application to uniqueness problems of differential equations. Acta Mathematica Academiae Scientiarum Hungaricae 1956, 7: 81-94. 10.1007/BF02022967
Cheung W-S: Some new nonlinear inequalities and applications to boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(9):2112-2128. 10.1016/j.na.2005.08.009
Choi SK, Deng S, Koo NJ, Zhang W:Nonlinear integral inequalities of Bihari-type without class
 . Mathematical Inequalities & Applications 2005,8(4):643-654.
. Mathematical Inequalities & Applications 2005,8(4):643-654.Horváth L: Generalizations of special Bihari type integral inequalities. Mathematical Inequalities & Applications 2005,8(3):441-449.
Lungu N: On some Gronwall-Bihari-Wendorff-type inequalities. Fixed Point Theory 2002, 3: 249-254.
Pachpatte BG: On generalizations of Bihari's inequality. Soochow Journal of Mathematics 2005,31(2):261-271.
Pachpatte BG: Integral inequalities of the Bihari type. Mathematical Inequalities & Applications 2002,5(4):649-657.
Pinto M: Integral inequalities of Bihari-type and applications. Funkcialaj Ekvacioj 1990,33(3):387-403.
Ye H, Gao J, Ding Y: A generalized Gronwall inequality and its application to a fractional differential equation. Journal of Mathematical Analysis and Applications 2007,328(2):1075-1081. 10.1016/j.jmaa.2006.05.061
Zhang W, Deng S: Projected Gronwall-Bellman's inequality for integrable functions. Mathematical and Computer Modelling 2001,34(3-4):393-402. 10.1016/S0895-7177(01)00070-X
Cheung W-S: Some discrete nonlinear inequalities and applications to boundary value problems for difference equations. Journal of Difference Equations and Applications 2004,10(2):213-223. 10.1080/10236190310001604238
Cheung W-S, Ren J: Discrete non-linear inequalities and applications to boundary value problems. Journal of Mathematical Analysis and Applications 2006,319(2):708-724. 10.1016/j.jmaa.2005.06.064
Deng S, Prather C: Nonlinear discrete inequalities of Bihari-type. submitted
Pachpatte BG: On Bihari like integral and discrete inequalities. Soochow Journal of Mathematics 1991,17(2):213-232.
Phat VN, Park JY: On the Gronwall inequality and asymptotic stability of nonlinear discrete systems with multiple delays. Dynamic Systems and Applications 2001,10(4):577-588.
Popenda J, Agarwal RP: Discrete Gronwall inequalities in many variables. Computers & Mathematics with Applications 1999,38(1):63-70. 10.1016/S0898-1221(99)00169-8
Tao L, Yong H: A generalization of discrete Gronwall inequality and its application to weakly singular Volterra integral equation of the second kind. Journal of Mathematical Analysis and Applications 2003,282(1):56-62. 10.1016/S0022-247X(02)00369-4
Wong F-H, Yeh C-C, Hong C-H: Gronwall inequalities on time scales. Mathematical Inequalities & Applications 2006,9(1):75-86.
Pachpatte BG: Integral and Finite Difference Inequalities and Applications, North-Holland Mathematics Studies. Volume 205. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:x+309.
Acknowledgments
This paper was supported by Guangdong Provincial natural science Foundation (07301595). The authors would like to thank Professor Boling Guo for his great help.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, Y., Li, X. & Deng, S. Nonlinear Delay Discrete Inequalities and Their Applications to Volterra Type Difference Equations. Adv Differ Equ 2010, 795145 (2010). https://doi.org/10.1155/2010/795145
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/795145
 is nonnegative for
is nonnegative for 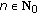 and
and 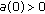 ;
;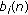
 are nondecreasing for
are nondecreasing for  , the range of each
, the range of each 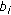 belongs to
belongs to  , and
, and 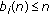 ;
;
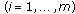 are nonnegative for
are nonnegative for 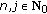 ;
;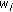
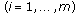 are continuous and nondecreasing functions on
are continuous and nondecreasing functions on  and are positive on
and are positive on 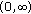 . They satisfy the relationship
. They satisfy the relationship  where
where 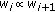 means that
means that 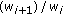 is nondecreasing on
is nondecreasing on  (see [
(see [ is defined by (2.3) and
is defined by (2.3) and  when all
when all 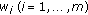 satisfy
satisfy  . Different choices of
. Different choices of  in
in  do not affect our results (see [
do not affect our results (see [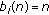 for
for 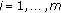 , then (2.1) gives the estimate of the following inequality:
, then (2.1) gives the estimate of the following inequality: independent variables. Journal of Mathematical Analysis and Applications 1982,85(1):192-196. 10.1016/0022-247X(82)90034-8
independent variables. Journal of Mathematical Analysis and Applications 1982,85(1):192-196. 10.1016/0022-247X(82)90034-8 . Mathematical Inequalities & Applications 2005,8(4):643-654.
. Mathematical Inequalities & Applications 2005,8(4):643-654.