- Research Article
- Open access
- Published:
Time-Scale-Dependent Criteria for the Existence of Positive Solutions to 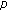 -Laplacian Multipoint Boundary Value Problem
-Laplacian Multipoint Boundary Value Problem
Advances in Difference Equations volume 2010, Article number: 746106 (2010)
Abstract
By virtue of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem, we analytically establish several sufficient criteria for the existence of at least two or three positive solutions in the  -Laplacian dynamic equations on time scales with a particular kind of
-Laplacian dynamic equations on time scales with a particular kind of  -Laplacian and
-Laplacian and  -point boundary value condition. It is this kind of boundary value condition that leads the established criteria to be dependent on the time scales. Also we provide a representative and nontrivial example to illustrate a possible application of the analytical results established. We believe that the established analytical results and the example together guarantee the reliability of numerical computation of those
-point boundary value condition. It is this kind of boundary value condition that leads the established criteria to be dependent on the time scales. Also we provide a representative and nontrivial example to illustrate a possible application of the analytical results established. We believe that the established analytical results and the example together guarantee the reliability of numerical computation of those  -Laplacian and
-Laplacian and  -point boundary value problems on time scales.
-point boundary value problems on time scales.
1. Introduction
The investigation of dynamic equations on time scales, originally attributed to Stefan Hilger's seminal work [1, 2] two decades ago, is now undergoing a rapid development. It not only unifies the existing results and principles for both differential equations and difference equations with constant time stepsize but also invites novel and nontrivial discussions and theories for hybrid equations on various types of time scales [3–11]. On the other hand, along with the significant development of the theories, practical applications of dynamic equations on time scales in mathematical modeling of those real processes and phenomena, such as the population dynamics, the economic evolutions, the chemical kinetics, and the neural signal processing, have been becoming richer and richer [12, 13].
As one of the focal topics in the research of dynamic equations on time scales, the study of boundary value problems for some specific dynamic equations on time scales recently has elicited a great deal of attention from mathematical community [14–33]. In particular, a series of works have been presented to discuss the existence of positive solutions in the boundary value problems for the second-order equations on time scales [14–21]. More recently, some analytical criteria have been established for the existence of positive solutions in some specific boundary value problems for the  -Laplacian dynamic equations on time scales [22, 33].
-Laplacian dynamic equations on time scales [22, 33].
Concretely, He [25] investigated the following dynamic equation:

with the boundary value conditions

Here and throughout,  is supposed to be a time scale; that is,
is supposed to be a time scale; that is,  is any nonempty closed subset of real numbers in
is any nonempty closed subset of real numbers in  with order and topological structure defined in a canonical way. The closed interval in
with order and topological structure defined in a canonical way. The closed interval in  is defined as
is defined as  . Accordingly, the open interval and the half-open interval could be defined, respectively. In addition, it is assumed that
. Accordingly, the open interval and the half-open interval could be defined, respectively. In addition, it is assumed that  ,
,  ,
,  ,
,  , and
, and  for some positive constants
for some positive constants  and
and  . Moreover,
. Moreover,  is supposed to be the
is supposed to be the  -Laplacian operator, that is,
-Laplacian operator, that is,  and
and  , in which
, in which  and
and  . With these configurations and with the aid of the Avery-Henderson fixed point theorem [34], He established the criteria for the existence of at least two positive solutions in (1.1) fulfilling the boundary value conditions (1.2).
. With these configurations and with the aid of the Avery-Henderson fixed point theorem [34], He established the criteria for the existence of at least two positive solutions in (1.1) fulfilling the boundary value conditions (1.2).
Later on, Su and Li [24] discussed the dynamic equation (1.1) which satisfies the boundary value conditions

where  ,
,  , and
, and  for
for  . By virtue of the five functionals fixed point theorem [35], they proved that the dynamic equation (1.1) with conditions (1.3) has three positive solutions at least. Meanwhile, He and Li in [26], studied the dynamic equation (1.1) satisfying either the boundary value conditions
. By virtue of the five functionals fixed point theorem [35], they proved that the dynamic equation (1.1) with conditions (1.3) has three positive solutions at least. Meanwhile, He and Li in [26], studied the dynamic equation (1.1) satisfying either the boundary value conditions

or the conditions

In the light of the five functionals fixed point theorem, they established the criteria for the existence of at least three solutions for the dynamic equation (1.1) either with conditions (1.4) or with conditions (1.5).
More recently, Yaslan [27, 28] investigated the dynamic equation:

which satisfies either the boundary value conditions

or the conditions

Here,  ,
,  ,
,  , and
, and  . Indeed, Yaslan analytically established the conditions for the existence of at least two or three positive solutions in these boundary value problems by virtue of the Avery-Henderson fixed point theorem and the Leggett-Williams fixed point theorem [36]. It is worthwhile to mention that these theoretical results are novel even for some special cases on time scales, such as the conventional difference equations with fixed time stepsize and the ordinary differential equations.
. Indeed, Yaslan analytically established the conditions for the existence of at least two or three positive solutions in these boundary value problems by virtue of the Avery-Henderson fixed point theorem and the Leggett-Williams fixed point theorem [36]. It is worthwhile to mention that these theoretical results are novel even for some special cases on time scales, such as the conventional difference equations with fixed time stepsize and the ordinary differential equations.
Motivated by the aforementioned results and techniques in coping with those boundary value problems on time scales, we thus turn to investigate the possible existence of multiple positive solutions for the following one-dimensional  -Laplacian dynamic equation:
-Laplacian dynamic equation:

with the  -Laplacian and
-Laplacian and  -point boundary value conditions:
-point boundary value conditions:

In the following discussion, we implement three hypotheses as follows.
-
(H1) One has
 for
for  ,
, 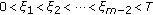 , and
, and  .
. -
(H2)One has that
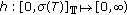 is left dense continuous (
is left dense continuous ( -continuous), and there exists a
-continuous), and there exists a 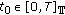 such that
such that 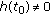 . Also
. Also 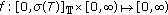 is continuous.
is continuous. -
(H3)Both
 and
and  are continuously odd functions defined on
are continuously odd functions defined on  . There exist two positive numbers
. There exist two positive numbers 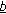 and
and  such that, for any
such that, for any 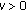 ,
,

and that

It is clear that, together with conditions (1.10) and the above hypotheses ( )–(
)–( ), the dynamic equation (1.9) not only covers the corresponding boundary value problems in the literature, but even nontrivially generalizes these problems to a much wider class of boundary value problems on time scales. Also it is valuable to mention that condition (1.12) in hypothesis (
), the dynamic equation (1.9) not only covers the corresponding boundary value problems in the literature, but even nontrivially generalizes these problems to a much wider class of boundary value problems on time scales. Also it is valuable to mention that condition (1.12) in hypothesis ( ) is necessarily relevant to the graininess operator
) is necessarily relevant to the graininess operator  around the time instant
around the time instant  . Such kind of condition has not been required in the literature, to the best of authors' knowledge. Thus, this paper analytically establishes some new and time-scale-dependent criteria for the existence of at least double or triple positive solutions in the boundary value problems (1.9) and (1.10) by virtue of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem. Indeed, these obtained criteria significantly extend the results existing in [26–28].
. Such kind of condition has not been required in the literature, to the best of authors' knowledge. Thus, this paper analytically establishes some new and time-scale-dependent criteria for the existence of at least double or triple positive solutions in the boundary value problems (1.9) and (1.10) by virtue of the Avery-Henderson fixed point theorem and the five functionals fixed point theorem. Indeed, these obtained criteria significantly extend the results existing in [26–28].
The remainder of the paper is organized as follows. Section 2 preliminarily provides some lemmas which are crucial to the following discussion. Section 3 analytically establishes the criteria for the existence of at least two positive solutions in the boundary value problems (1.9) and (1.10) with the aid of the Avery-Henderson fixed point theorem. Section 4 gives some sufficient conditions for the existence of at least three positive solutions by means of the five functionals fixed point theorem. More importantly, Section 5 provides a representative and nontrivial example to illustrate a possible application of the obtained analytical results on dynamic equations on time scales. Finally, the paper is closed with some concluding remarks.
2. Preliminaries
In this section, we intend to provide several lemmas which are crucial to the proof of the main results in this paper. However, for concision, we omit the introduction of those elementary notations and definitions, which can be found in [11, 12, 33] and references therein.
The following lemmas are based on the following linear boundary value problems:

Lemma 2.1.
Assume that  . Then, for
. Then, for  , the linear boundary value problems (2.1) have a unique solution satisfying
, the linear boundary value problems (2.1) have a unique solution satisfying

for all  .
.
Proof.
According to the formula  introduced in [12], we have
introduced in [12], we have

Thus, we obtain that

and that

To this end, it is not hard to check that  satisfies (2.2), which implies that
satisfies (2.2), which implies that  is a solution of the problems (2.1).
is a solution of the problems (2.1).
Furthermore, in order to verify the uniqueness, we suppose that both  and
and  are the solutions of the problems (2.1). Then, we have
are the solutions of the problems (2.1). Then, we have



According to Theorem  in [37], (2.6) further yields
in [37], (2.6) further yields

Hence, from (2.7) and (2.9), the assumption  , and the definition of the
, and the definition of the  -Laplacian operator, it follows that
-Laplacian operator, it follows that

This equation, together with (2.8), further implies

which consequently leads to the completion of the proof, that is,  specified in (2.2) is the unique solution of the problems (2.1).
specified in (2.2) is the unique solution of the problems (2.1).
Lemma 2.2.
Assume that  and that
and that  . If
. If  , then the unique solution of the problems (2.1) satisfies
, then the unique solution of the problems (2.1) satisfies

Proof.
By (2.2) specified in Lemma 2.1, we get

Thus,  is nonincreasing in the interval
is nonincreasing in the interval  . In addition, notice that
. In addition, notice that

The last term in the above estimation is no less than zero because of the assumptions. Thus, from the monotonicity of  , we get
, we get

which completes the proof.
Now, denote that  and that
and that  , where
, where  . Thus, it is easy to verify that
. Thus, it is easy to verify that  endowed with
endowed with  becomes a Banach space. Furthermore, define a cone, denoted by
becomes a Banach space. Furthermore, define a cone, denoted by  , through,
, through,

Also, for a given positive real number  , define a function set
, define a function set  by
by

Naturally, we denote that  and that
and that  . With these settings, we have the following properties.
. With these settings, we have the following properties.
Lemma 2.3.
If  then
then  for any
for any  ,
,  for any pair of
for any pair of  with
with  .
.
The proof of this lemma, which could be found in [26, 28], is directly from the specific construction of the set  . Next, let us construct a map
. Next, let us construct a map  through
through

for any  . Then, through a standard argument [33], it is not hard to validate the following properties on this map.
. Then, through a standard argument [33], it is not hard to validate the following properties on this map.
Lemma 2.4.
Assume that the hypotheses  are all fulfilled. Then,
are all fulfilled. Then,  , and
, and  is completely continuous.
is completely continuous.
3. At Least Two Positive Solutions in Boundary Value Problems
In this section, we aim to adopt the well-known Avery-Henderson fixed point theorem to prove the existence of at least two positive solutions in the boundary value problems (1.9) and (1.10). For the sake of self-containment, we first state the Avery-Henderson fixed point theorem as follows.
Theorem 3.1 (see [34]).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . For each
. For each  , set
, set  . Let
. Let and
and  be increasing, nonnegative continuous functionals on
be increasing, nonnegative continuous functionals on  , and let
, and let  be a nonnegative continuous functional on
be a nonnegative continuous functional on  with
with  such that, for some
such that, for some  and
and  ,
,

for all  . Suppose that there exist a completely continuous operator
. Suppose that there exist a completely continuous operator  and three positive numbers
and three positive numbers  such that
such that

and  for all
for all  ,
,  for all
for all  , and
, and  and
and  for all
for all  . Then, the operator
. Then, the operator  has at least two fixed points, denoted by
has at least two fixed points, denoted by  and
and  , belonging to
, belonging to  and satisfying
and satisfying  with
with  and
and  with
with  .
.
Now, set  and select
and select  satisfying
satisfying  . Denote, respectively, that
. Denote, respectively, that

Hence, we are in a position to obtain the following results.
Theorem 3.2.
Assume that the hypotheses  all hold and that there exist positive real numbers
all hold and that there exist positive real numbers  ,
,  ,
,  such that
such that

In addition, assume that  satisfies the following conditions:
satisfies the following conditions:
-
(C1)
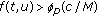 for
for 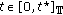 and
and  ;
; -
(C2)
 for
for 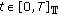 and
and  ;
; -
(C3)
 for
for 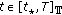 and
and 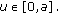
Then, the boundary value problems (1.9) and (1.10) have at least two positive solutions  and
and  such that
such that

Proof.
Construct the cone  and the operator
and the operator  as specified in (2.16) and (2.18), respectively. In addition, define the increasing, nonnegative, and continuous functionals
as specified in (2.16) and (2.18), respectively. In addition, define the increasing, nonnegative, and continuous functionals  ,
,  , and
, and  on
on  , respectively, by
, respectively, by

Evidently,  for each
for each  .
.
In addition, for each  , Lemma 2.3 manifests that
, Lemma 2.3 manifests that  . Thus, we have
. Thus, we have

for each  . Also, notice that
. Also, notice that  for
for  and
and  . Furthermore, from Lemma 2.4, it follows that the operator
. Furthermore, from Lemma 2.4, it follows that the operator  is completely continuous.
is completely continuous.
In what follows, we are to verify that all the conditions of Theorem 3.1 are satisfied with respect to the operator  .
.
Let  . Then,
. Then,  . This implies that
. This implies that  for
for  , which, combined with (3.7), yields
, which, combined with (3.7), yields

for  . Because of assumption (
. Because of assumption ( ),
),  for
for  . According to the specific form in (2.18), Lemma 2.3, and the property
. According to the specific form in (2.18), Lemma 2.3, and the property  , we obtain that
, we obtain that

Thus, condition (i) in Theorem 3.1 is satisfied.
Next, consider  . In such a case, we have
. In such a case, we have  , which implies that
, which implies that  for
for  . Analogously, it follows from (3.7) that, for all
. Analogously, it follows from (3.7) that, for all  ,
,

Therefore, we obtain  for
for  . This, combined with assumption (
. This, combined with assumption ( ), gives
), gives  for all
for all  . Thus, we have
. Thus, we have

which consequently implies the validity of condition (ii) in Theorem 3.1.
Finally, notice that the constant functions  , so that
, so that  . Let
. Let  . Then, we get
. Then, we get  . This with assumption
. This with assumption  implies that
implies that  and
and  for all
for all  . Similarly, we have
. Similarly, we have

Indeed, the validity of condition (iii) in Theorem 3.1 is verified.
According to Theorem 3.1, we consequently approach the conclusion that the boundary value problems (1.9) and (1.10) possess at least two positive solutions, denoted by  and
and  , satisfying
, satisfying  with
with  and
and  with
with  , respectively.
, respectively.
4. At Least Three Positive Solutions in Boundary Value Problems
In this section, we are to prove the existence of at least three positive solutions in the boundary value problems (1.9) and (1.10) by using the five functionals fixed point theorem which is attributed to Avery [35].
Let  be nonnegative continuous convex functionals on
be nonnegative continuous convex functionals on  .
.  and
and  are supposed to be nonnegative continuous concave functionals on
are supposed to be nonnegative continuous concave functionals on  . Thus, for nonnegative real numbers
. Thus, for nonnegative real numbers  ,
,  ,
,  ,
,  , and
, and  , define five convex sets, respectively, by
, define five convex sets, respectively, by

Theorem 4.1 (see [35]).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . Suppose that
. Suppose that  and
and  are nonnegative continuous concave functionals on
are nonnegative continuous concave functionals on  , and that
, and that  ,
,  , and
, and  are nonnegative continuous convex functionals on
are nonnegative continuous convex functionals on  such that, for some positive numbers
such that, for some positive numbers  and
and  ,
,

for all  . In addition, suppose that
. In addition, suppose that  is a completely continuous operator and that there exist nonnegative real numbers
is a completely continuous operator and that there exist nonnegative real numbers  with
with  such that
such that
-
(i)
 and
and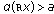 for
for 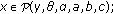
-
(ii)
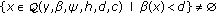 and
and 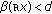 for
for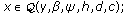
-
(iii)
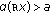 for
for 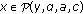 with
with 
-
(iv)
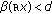 for
for  with
with 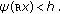
Then the operator  admits at least three fixed points
admits at least three fixed points  ,
, ,
, satisfying
satisfying  ,
,  , and
, and  with
with  , respectively.
, respectively.
With this theorem, we are now in a position to establish the following result on the existence of at least three solutions in the boundary value problems (1.9) and (1.10).
Theorem 4.2.
Suppose that the hypotheses  are all fulfilled. Assume that there exist positive real numbers
are all fulfilled. Assume that there exist positive real numbers  ,
,  ,
,  such that
such that

Also assume that  satisfies the following conditions:
satisfies the following conditions:
-
(C1)
 for
for 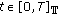 and
and  ;
; -
(C2)
 for
for 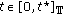 and
and 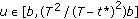 ;
; -
(C3)
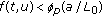 for
for 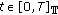 and
and  .
.
Then, the boundary value problems (1.9) and (1.10) admit at least three solutions  ,
,  , and
, and  , defined on
, defined on  , satisfying, respectively,
, satisfying, respectively,

Proof.
Let the cone  be as constructed in (2.16) and the operator
be as constructed in (2.16) and the operator  as defined in (2.18). Define, respectively, the nonnegative continuous concave functionals on the
as defined in (2.18). Define, respectively, the nonnegative continuous concave functionals on the  as follows:
as follows:

Thus, we get  for
for  . Moreover, from Lemma 2.3, it follows that
. Moreover, from Lemma 2.3, it follows that

for  . Next, we intend to verify that all the conditions in Theorem 4.1 hold with respect to the operator
. Next, we intend to verify that all the conditions in Theorem 4.1 hold with respect to the operator  .
.
To this end, arbitrarily pick up a function  . Then,
. Then,  , which, combined with (4.6), implies that
, which, combined with (4.6), implies that  for
for  and
and  . Thus, we have
. Thus, we have  for
for  , owing to assumption (
, owing to assumption ( ). Moreover, since
). Moreover, since  , we have
, we have

This, with Lemma 2.4, clearly manifests that the operator  is completely continuous.
is completely continuous.
Moreover, the set

is not empty, because the constant function  belongs to the set
belongs to the set  . Analogously, the set
. Analogously, the set

is nonempty, since  . For particular
. For particular  , a utilization of (4.6) produces
, a utilization of (4.6) produces

for  . According to assumption (
. According to assumption ( ), we thus obtain
), we thus obtain

for all  . Hence, it follows from (4.11) and Lemma 2.3 that
. Hence, it follows from (4.11) and Lemma 2.3 that

This definitely verifies the validity of condition  in Theorem 4.1.
in Theorem 4.1.
Next, let us consider  . In this case, we get
. In this case, we get

for  . Thus, an adoption of the assumption (
. Thus, an adoption of the assumption ( ) yields
) yields  . Furthermore, we have
. Furthermore, we have

Accordingly, the validity of condition ( ) in Theorem 4.1 is verified.
) in Theorem 4.1 is verified.
Aside from conditions ( ) and (
) and ( ), we are finally to verify the validity of conditions (
), we are finally to verify the validity of conditions ( ) and (
) and ( ). For this purpose, on the one hand, consider
). For this purpose, on the one hand, consider  with
with  . Thus, we have
. Thus, we have

On the other hand, consider  with
with  . In such a case, we obtain that
. In such a case, we obtain that

Therefore, both conditions ( ) and (
) and ( ) in Theorem 4.1 are satisfied. Consequently, by virtue of Theorem 4.1, the boundary value problems (1.9) and (1.10) have at least three positive solutions circumscribed on
) in Theorem 4.1 are satisfied. Consequently, by virtue of Theorem 4.1, the boundary value problems (1.9) and (1.10) have at least three positive solutions circumscribed on  satisfying
satisfying  ,
,  , and
, and  with
with  .
.
5. A Specific Example
In this section, we provide a representative and nontrivial example to clearly illustrate the feasibility of the time-scale-dependent results of dynamic equations with boundary value conditions that are obtained in the preceding section.
Construct a nontrivial time-scale set as

Take all the parameters in problems (1.9) and (1.10) as follows: 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  , so that
, so that  . For simplicity but without loss of generality, set
. For simplicity but without loss of generality, set  . Also notice that there exist countable right-scattered points
. Also notice that there exist countable right-scattered points  . Then, it is easy to validate the condition
. Then, it is easy to validate the condition

which is dependent on the time scale property around the time instant  . Furthermore, implementing the integral formula [38]:
. Furthermore, implementing the integral formula [38]:

we concretely obtain that

Particularly, take the function in dynamic equation as

This kind of function is omnipresent in the mathematical modeling of biological or chemical processes. Then it allows us to properly set the other parameters as  ,
,  , and
, and  . It is evident that these parameters satisfy
. It is evident that these parameters satisfy

Now, we can verify the validity of conditions  in Theorem 4.2. Indeed, direct computations yield:
in Theorem 4.2. Indeed, direct computations yield:

as  and
and  ,
,

as  and
and  , and
, and

as  and
and  . Hence, conditions
. Hence, conditions  in Theorem 4.2 are satisfied for the above specified functions and parameters. Therefore, in the light of Theorem 4.2, we conclude that the dynamic equation on the specified time scales
in Theorem 4.2 are satisfied for the above specified functions and parameters. Therefore, in the light of Theorem 4.2, we conclude that the dynamic equation on the specified time scales

with the boundary value conditions

has at least three positive solutions defined on  satisfying
satisfying  ,
,  , and
, and  with
with  .
.
6. Concluding Remarks
In this paper, some novel and time-scale-dependent sufficient conditions are established for the existence of multiple positive solutions in a specific kind of boundary value problems on time scales. This kind of boundary value problems not only includes the problems discussed in the literature but also is adapted to more general cases. The well-known Avery-Henderson fixed point theorem and the five functionals fixed point theorem are adopted in the arguments.
It is valuable to mention that the writing form of the ending point of the interval on time scales should be accurately specified in dealing with different kind of boundary value conditions. Any inaccurate expression may lead to a problematic or incomplete discussion. Also it is noted that some other fixed point theorems and degree theories may be adapted to dealing with various boundary value problems on time scales. In addition, future directions for further generalization of the boundary value problem on time scales may include the generalization of the  -Laplacian operator to increasing homeomorphism and homeomorphism, which has been investigated in [39] for the nonlinear boundary value of ordinary differential equations; the allowance of the function
-Laplacian operator to increasing homeomorphism and homeomorphism, which has been investigated in [39] for the nonlinear boundary value of ordinary differential equations; the allowance of the function  to change sign, which has been discussed in [31] and needs more detailed and rigorous investigations.
to change sign, which has been discussed in [31] and needs more detailed and rigorous investigations.
References
Aulbach B, Hilger S: Linear dynamic processes with inhomogeneous time scale. In Nonlinear Dynamics and Quantum Dynamical Systems (Gaussig, 1990), Mathematics Research. Volume 59. Akademie, Berlin, Germany; 1990:9-20.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Agarwal RP, Bohner M, Rehak P: Half-linear dynamic equations. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Vol. 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:1-57.
Lakshmikantham V, Sivasundaram S, Kaymakcalan B: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Hoffacker J, Tisdell CC: Stability and instability for dynamic equations on time scales. Computers & Mathematics with Applications 2005,49(9-10):1327-1334. 10.1016/j.camwa.2005.01.016
Zhong W, Lin W, Ruan J: The generalized invariance principle for dynamic equations on time scales. Applied Mathematics and Computation 2007,184(2):557-565. 10.1016/j.amc.2006.06.056
Wu H, Zhou Z: Stability for first order delay dynamic equations on time scales. Computers & Mathematics with Applications 2007,53(12):1820-1831. 10.1016/j.camwa.2006.09.011
Otero-Espinar V, Vivero DR: Uniqueness and existence results for initial value problems on time scales through a reciprocal problem and applications. Computers & Mathematics with Applications 2009,58(4):700-710. 10.1016/j.camwa.2009.02.030
Anderson DR, Wong PJY: Positive solutions for second-order semipositone problems on time scales. Computers & Mathematics with Applications 2009,58(2):281-291. 10.1016/j.camwa.2009.02.033
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Bohner M, Peterson A: Dynamic Equations on Time Scales. An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Atici FM, Biles DC, Lebedinsky A: An application of time scales to economics. Mathematical and Computer Modelling 2006,43(7-8):718-726. 10.1016/j.mcm.2005.08.014
Akin E: Boundary value problems for a differential equation on a measure chain. Panamerican Mathematical Journal 2000,10(3):17-30.
Agarwal RP, O'Regan D: Triple solutions to boundary value problems on time scales. Applied Mathematics Letters 2000,13(4):7-11. 10.1016/S0893-9659(99)00200-1
Agarwal RP, O'Regan D: Nonlinear boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2001,44(4):527-535. 10.1016/S0362-546X(99)00290-4
Anderson DR: Solutions to second-order three-point problems on time scales. Journal of Difference Equations and Applications 2002,8(8):673-688. 10.1080/1023619021000000717
Anderson DR: Nonlinear triple-point problems on time scales. Electronic Journal of Differential Equations 2004, (47):-12.
Kaufmann ER: Positive solutions of a three-point boundary-value problem on a time scale. Electronic Journal of Differential Equations 2003, (82):-11.
DaCunha JJ, Davis JM, Singh PK: Existence results for singular three point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004,295(2):378-391. 10.1016/j.jmaa.2004.02.049
He Z:Existence of two solutions of
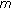 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051Sun H-R, Li W-T:Multiple positive solutions for
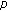 -Laplacian
-Laplacian 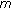 -point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009
-point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009Sun H-R, Li W-T:Existence theory for positive solutions to one-dimensional
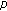 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004Su Y-H, Li W-T:Triple positive solutions of
 -point BVPs for
-point BVPs for  -Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018
-Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018He Z:Double positive solutions of three-point boundary value problems for
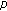 -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012
-Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012He Z, Li L:Multiple positive solutions for the one-dimensional
 -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021
-Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021Yaslan İ: Multiple positive solutions for nonlinear three-point boundary value problems on time scales. Computers & Mathematics with Applications 2008,55(8):1861-1869. 10.1016/j.camwa.2007.07.005
Yaslan İ: Existence of positive solutions for nonlinear three-point problems on time scales. Journal of Computational and Applied Mathematics 2007,206(2):888-897. 10.1016/j.cam.2006.08.033
Anderson DR, Karaca IY: Higher-order three-point boundary value problem on time scales. Computers & Mathematics with Applications 2008,56(9):2429-2443. 10.1016/j.camwa.2008.05.018
Anderson DR, Avery R, Henderson J:Existence of solutions for a one dimensional
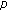 -Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416
-Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416Sang Y, Su H, Xu F:Positive solutions of nonlinear
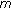 -point BVP for an increasing homeomorphism and homomorphism with sign changing nonlinearity on time scales. Computers & Mathematics with Applications 2009,58(2):216-226. 10.1016/j.camwa.2009.03.106
-point BVP for an increasing homeomorphism and homomorphism with sign changing nonlinearity on time scales. Computers & Mathematics with Applications 2009,58(2):216-226. 10.1016/j.camwa.2009.03.106Sun H-R:Triple positive solutions for
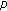 -Laplacian
-Laplacian 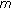 -point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083
-point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083Zhong W, Lin W:Existence of positive solutions in generalized boundary value problem for
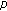 -Laplacian dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-19.
-Laplacian dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-19.Avery RI, Henderson J: Two positive fixed points of nonlinear operators on ordered Banach spaces. Communications on Applied Nonlinear Analysis 2001,8(1):27-36.
Avery RI: A generalization of the Leggett-Williams fixed point theorem. Mathematical Sciences Research Hot-Line 1999,3(7):9-14.
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana University Mathematics Journal 1979,28(4):673-688. 10.1512/iumj.1979.28.28046
Guseinov GSh: Integration on time scales. Journal of Mathematical Analysis and Applications 2003,285(1):107-127. 10.1016/S0022-247X(03)00361-5
Cabada A, Vivero DR:Expression of the Lebesgue
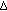 -integral on time scales as a usual Lebesgue integral: application to the calculus of
-integral on time scales as a usual Lebesgue integral: application to the calculus of 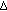 -antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028
-antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028Bereanu C, Mawhin J:Existence and multiplicity results for some nonlinear problems with singular
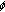 -Laplacian. Journal of Differential Equations 2007,243(2):536-557. 10.1016/j.jde.2007.05.014
-Laplacian. Journal of Differential Equations 2007,243(2):536-557. 10.1016/j.jde.2007.05.014
Acknowledgments
This paper was supported by the NNSF of China (Grants nos. 10501008 and 60874121) and by the Rising-Star Program Foundation of Shanghai, China (Grant no. 07QA14002). The authors are grateful to the referee and editors for their very helpful suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhong, W., Lin, W. Time-Scale-Dependent Criteria for the Existence of Positive Solutions to 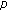 -Laplacian Multipoint Boundary Value Problem.
Adv Differ Equ 2010, 746106 (2010). https://doi.org/10.1155/2010/746106
-Laplacian Multipoint Boundary Value Problem.
Adv Differ Equ 2010, 746106 (2010). https://doi.org/10.1155/2010/746106
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/746106
 for
for  ,
, 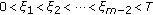 , and
, and  .
.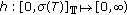 is left dense continuous (
is left dense continuous ( -continuous), and there exists a
-continuous), and there exists a 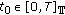 such that
such that 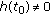 . Also
. Also 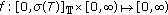 is continuous.
is continuous. and
and  are continuously odd functions defined on
are continuously odd functions defined on  . There exist two positive numbers
. There exist two positive numbers 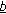 and
and  such that, for any
such that, for any 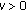 ,
,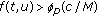 for
for 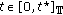 and
and  ;
; for
for 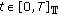 and
and  ;
; for
for 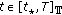 and
and 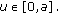
 and
and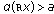 for
for 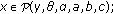
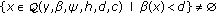 and
and 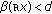 for
for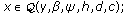
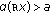 for
for 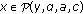 with
with 
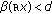 for
for  with
with 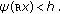
 for
for 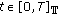 and
and  ;
; for
for 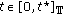 and
and 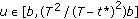 ;
;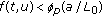 for
for 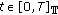 and
and  .
.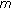 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051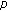 -Laplacian
-Laplacian 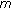 -point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009
-point boundary value problems on time scales. Applied Mathematics and Computation 2006,182(1):478-491. 10.1016/j.amc.2006.04.009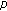 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217-248. 10.1016/j.jde.2007.06.004 -point BVPs for
-point BVPs for  -Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018
-Laplacian dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3811-3820. 10.1016/j.na.2007.10.018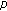 -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012
-Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304-315. 10.1016/j.cam.2004.12.012 -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021
-Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2007,45(1-2):68-79. 10.1016/j.mcm.2006.03.021 -Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416
-Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889-896. 10.1080/10236190410001731416 -point BVP for an increasing homeomorphism and homomorphism with sign changing nonlinearity on time scales. Computers & Mathematics with Applications 2009,58(2):216-226. 10.1016/j.camwa.2009.03.106
-point BVP for an increasing homeomorphism and homomorphism with sign changing nonlinearity on time scales. Computers & Mathematics with Applications 2009,58(2):216-226. 10.1016/j.camwa.2009.03.106 -Laplacian
-Laplacian  -point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083
-point boundary value problem on time scales. Computers & Mathematics with Applications 2009,58(9):1736-1741. 10.1016/j.camwa.2009.07.083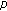 -Laplacian dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-19.
-Laplacian dynamic equations on time scales. Advances in Difference Equations 2009, 2009:-19.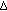 -integral on time scales as a usual Lebesgue integral: application to the calculus of
-integral on time scales as a usual Lebesgue integral: application to the calculus of 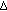 -antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028
-antiderivatives. Mathematical and Computer Modelling 2006,43(1-2):194-207. 10.1016/j.mcm.2005.09.028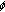 -Laplacian. Journal of Differential Equations 2007,243(2):536-557. 10.1016/j.jde.2007.05.014
-Laplacian. Journal of Differential Equations 2007,243(2):536-557. 10.1016/j.jde.2007.05.014