- Research Article
- Open access
- Published:
A Converse Lyapunov Theorem and Robustness with Respect to Unbounded Perturbations for Exponential Dissipativity
Advances in Difference Equations volume 2010, Article number: 726347 (2010)
Abstract
This paper is concerned with the nonlinear system  . We give a converse Lyapunov theorem and prove robustness of uniform exponential dissipativity with respect to unbounded external perturbations, without assuming
. We give a converse Lyapunov theorem and prove robustness of uniform exponential dissipativity with respect to unbounded external perturbations, without assuming  being globally Lipschitz in
being globally Lipschitz in  .
.
1. Introduction
This paper is devoted to the following nonautonomous dynamical system:

where  is always assumed to be a continuous vector field which is locally Lipschitz in space variable
is always assumed to be a continuous vector field which is locally Lipschitz in space variable  . Our main aim is two-fold: one is to give a converse Lyapunov theorem for uniform exponential dissipativity, and the other is to study robustness of uniform exponential dissipativity to unbounded perturbations.
. Our main aim is two-fold: one is to give a converse Lyapunov theorem for uniform exponential dissipativity, and the other is to study robustness of uniform exponential dissipativity to unbounded perturbations.
In [1] Lyapunov introduced his famous sufficient conditions for asymptotic stability of (1.1), where we can also find the first contribution to the converse question, known as converse Lyapunov theorems. The answers have proved instrumental, over the years, in establishing robustness of various stability notions and have served as the starting point for many nonlinear control systems design concepts.
Recently Li and Kloeden [2] presented a converse Lyapunov theorem for exponential dissipativity of (1.1) in autonomous case with  being globally Lipschitz in
being globally Lipschitz in  . This result can be seen as a generalization of some classical ones on global exponential asymptotic stability (see, for instance, [3], etc.), and was used by the authors to study robustness of exponential dissipativity with respect to small time delays. Here we give a nonautonomous analog of the result; moreover, instead of assuming
. This result can be seen as a generalization of some classical ones on global exponential asymptotic stability (see, for instance, [3], etc.), and was used by the authors to study robustness of exponential dissipativity with respect to small time delays. Here we give a nonautonomous analog of the result; moreover, instead of assuming  to be globally Lipschitz in
to be globally Lipschitz in  , we only impose on
, we only impose on  the following weaker condition.
the following weaker condition.
-
(F1) There exists an
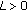 such that
such that (1.2)
(1.2)
where  denotes the inner product in
denotes the inner product in  .
.
Note that if  is globally Lipschitz in
is globally Lipschitz in  in a uniform manner with respect to
in a uniform manner with respect to  , then (F1) is automatically satisfied. However, we emphasize that this condition also allows nonglobally Lipschitz functions. An easy example is the function
, then (F1) is automatically satisfied. However, we emphasize that this condition also allows nonglobally Lipschitz functions. An easy example is the function  , which is clearly not globally Lipschitz. One observes that
, which is clearly not globally Lipschitz. One observes that

Then we study robustness property of uniform exponential dissipativity to perturbations. A basic problem in the dynamical theory concerns the robustness of global attractors under perturbations [4]. It is readily known that if a nonlinear system with a global attractor  is perturbed, then the perturbed one also has an attractor
is perturbed, then the perturbed one also has an attractor  which is near
which is near  , provided the perturbation is sufficiently small; see, for instance, [5, 6], and so forth. However, in general we only know that
, provided the perturbation is sufficiently small; see, for instance, [5, 6], and so forth. However, in general we only know that  is a local attractor. Whether (or under what circumstances) the global feature can be preserved is an interesting but, to the authors' knowledge, still open problem. (For concrete systems there is the hope that one may check the existence of global attractors by using the structure of the systems.) Since the dissipativity of a system usually implies the existence of the global attractor, in many cases the key point to answer the above problem is then reduced to examine the robustness of dissipativity under perturbations.
is a local attractor. Whether (or under what circumstances) the global feature can be preserved is an interesting but, to the authors' knowledge, still open problem. (For concrete systems there is the hope that one may check the existence of global attractors by using the structure of the systems.) Since the dissipativity of a system usually implies the existence of the global attractor, in many cases the key point to answer the above problem is then reduced to examine the robustness of dissipativity under perturbations.
Such a problem has obvious practical sense. Unfortunately the answer might be negative even if in some simple cases which seem to be very nice at a first glance, as indicated in Example 1.1 below (from which it is seen that dissipativity can be quite sensitive to perturbations).
Example 1.1 (see [7]).
Consider the scalar differential equation

It is easy to see that the equilibrium  is globally asymptotically stable, and consequently the system is dissipative. However, since for any
is globally asymptotically stable, and consequently the system is dissipative. However, since for any  there exists an
there exists an  such that
such that

we deduce that any solution  of the perturbed system
of the perturbed system

with  goes to
goes to  as
as  .
.
Note that  is bounded on
is bounded on  ; hence,
; hence,  is globally Lipschitz.
is globally Lipschitz.
In this present work we demonstrate that exponential dissipativity has nice robustness properties. Actually we will show that it is robust under some types of even unbounded perturbations.
This paper is organized as follows. In Section 2 we give a converse Lyapunov theorem mentioned above, and in Section 3 we prove robustness of exponential dissipativity.
2. A Converse Lyapunov Theorem
In this section we give a converse Lyapunov theorem which generalizes a recent result in [2]. Let us first recall some basic definitions and facts.
The upper right Dini sup-derivative of a function 

 is defined as
is defined as

Let  be an open interval, and let
be an open interval, and let  be an open subset of
be an open subset of  . Let
. Let 

 . For
. For  and
and 

 , define
, define

We call  the nonautonomous Dini sup-derivative of
the nonautonomous Dini sup-derivative of  at
at  along the vector
along the vector  . In case
. In case  is differentiable at
is differentiable at  , it is easy to see that
, it is easy to see that

Lemma 2.1.
Let  be an open subset of
be an open subset of  . Assume that the continuous function
. Assume that the continuous function 



 is Lipschitz in
is Lipschitz in  uniformly in
uniformly in 

 , that is, there exists an
, that is, there exists an  such that
such that

and let  . Then
. Then

Proof.
This basic fact is actually contained in [3], and so forth. Here we give a simple proof for the reader's convenience.
We observe that

Since  is Lipschitz in
is Lipschitz in  , one easily sees that
, one easily sees that

Therefore by definition we immediately deduce that

The proof is complete.
We will denote by  the solution operator of (1.1), that is, for each
the solution operator of (1.1), that is, for each  ,
,  is the unique solution of the system with initial value
is the unique solution of the system with initial value  .
.
Definition 2.2.
System (1.1) is said to be uniformly exponentially dissipative, if there exist positive numbers  ,
,  , and
, and  such that
such that

The main result in this section is the following theorem.
Theorem 2.3 (Converse Lyapunov Theorem).
Suppose that  satisfies the structure condition (F1). Assume that system (1.1) is uniformly exponentially dissipative.
satisfies the structure condition (F1). Assume that system (1.1) is uniformly exponentially dissipative.
Then there exists a function 



 satisfying
satisfying



for all  ,
, 

 and
and  , where
, where  ,
,  ,
,  ,
,  ,
,  , and
, and  are appropriate positive constants.
are appropriate positive constants.
Moreover, if  , namely, the system is uniformly exponentially asymptotically stable, then the constants
, namely, the system is uniformly exponentially asymptotically stable, then the constants  , and
, and  vanish.
vanish.
Proof.
Since the ODE system (1.1) is exponentially dissipative, there exist positive constants  ,
,  , and
, and  such that (2.9) holds. Let
such that (2.9) holds. Let

We first define a function  as follows: (The techniques used here are adopted from [2, 8], etc.)
as follows: (The techniques used here are adopted from [2, 8], etc.)

By (2.9) it is clear that

Let  ,
,  , and let
, and let  . Then
. Then

Taking inner product of this equation with  , by (F1) one finds that
, by (F1) one finds that

from which it can be easily seen that

Thus we deduce that

where  . Now for any
. Now for any  and
and  , we have
, we have

and it immediately follows by (2.9) that

where  is independent of
is independent of  . This shows that
. This shows that  satisfies (2.11).
satisfies (2.11).
Since

by the choice of  we have that
we have that

On the other hand, by Lemma 2.1 we find that

Setting  , one obtains that
, one obtains that

which indicates that  satisfies (2.12).
satisfies (2.12).
Now let us define another Lyapunov function  . For this purpose we take a nonnegative function
. For this purpose we take a nonnegative function  as
as

where  . Then
. Then

Indeed, if  , then the estimate clearly holds true. So we may assume without loss of generality that
, then the estimate clearly holds true. So we may assume without loss of generality that  with
with  . We have
. We have

Let

We claim that we actually have

Indeed, if  , then by (2.9) we deduce that
, then by (2.9) we deduce that  for all
for all  . On the other hand, by the definition of
. On the other hand, by the definition of  we have
we have  for all
for all  . Therefore in case
. Therefore in case  , one trivially has
, one trivially has

Now assume that  . Then by the choice of
. Then by the choice of  we find that
we find that

Since  and
and  is nondecreasing in
is nondecreasing in  , one immediately deduces that
, one immediately deduces that

which completes the proof of (2.30).
By (2.9), (2.19), and (2.27) we have

Therefore

Since  and
and  are arbitrary, we conclude that
are arbitrary, we conclude that

By the definition of  it is clear that
it is clear that

It immediately follows that

We also infer from (2.9) that

Therefore by definition of  and the monotonicity property of
and the monotonicity property of  , we have
, we have

In conclusion we have

Note that if  , then
, then

This implies that  is nonincreasing in
is nonincreasing in  .
.
Now set

Invoking (2.15), (2.21), and (2.25), we find that  is a Lyapunov function satisfying all the required properties in the theorem.
is a Lyapunov function satisfying all the required properties in the theorem.
In case  , it can be easily seen from the above argument that
, it can be easily seen from the above argument that  .
.
The proof is complete.
Remark 2.4.
If we assume that  is also locally Lipschitz in
is also locally Lipschitz in  , then
, then  is locally Lipschitz in
is locally Lipschitz in  as well. Now assume that
as well. Now assume that  is locally Lipschitz in
is locally Lipschitz in  . Then by the construction of
. Then by the construction of  and
and  one easily verifies that
one easily verifies that  is locally Lipschitz in
is locally Lipschitz in  . Consequently
. Consequently  has derivative in
has derivative in  almost everywhere.
almost everywhere.
3. Robustness of Exponential Dissipativity to Perturbations
As for the applications of the converse Lyapunov theorem given in Section 2, we consider in this section the robustness of exponential dissipativity to perturbations.
3.1. Robustness to External Perturbations
Consider the following perturbed system:

where  is a continuous function which corresponds to external perturbations.
is a continuous function which corresponds to external perturbations.
Denote by  the family of continuous functions
the family of continuous functions  that satisfies the following growth condition:
that satisfies the following growth condition:

where  is a continuous nonnegative function on
is a continuous nonnegative function on  with
with

for some  . Our main result in this part is contained in the following theorem.
. Our main result in this part is contained in the following theorem.
Theorem 3.1.
Assume that  is locally Lipschitz in
is locally Lipschitz in  and satisfies (F1). Suppose that the system (1.1) is uniformly exponentially dissipative.
and satisfies (F1). Suppose that the system (1.1) is uniformly exponentially dissipative.
Then there exists an  sufficiently small such that, for any
sufficiently small such that, for any  , the perturbed system (3.1) is uniformly exponentially dissipative.
, the perturbed system (3.1) is uniformly exponentially dissipative.
Remark 3.2.
Suppose that  satisfies a sublinear growth condition
satisfies a sublinear growth condition

where  , and
, and  is as in (3.3). Then one easily verifies that, for any
is as in (3.3). Then one easily verifies that, for any  , there exists a
, there exists a  such that
such that

namely,  . Hence the conclusion of the theorem naturally holds.
. Hence the conclusion of the theorem naturally holds.
Proof of Theorem 3.1.
Let  be the Lyapunov function of the unperturbed system given in Theorem 2.3, and take
be the Lyapunov function of the unperturbed system given in Theorem 2.3, and take  , where
, where  and
and  are the constants in (2.11) and (2.12). We show that for any
are the constants in (2.11) and (2.12). We show that for any  the perturbed system (3.1) is uniformly exponentially dissipative.
the perturbed system (3.1) is uniformly exponentially dissipative.
For simplicity in writing we set

Let  be any solution of the perturbed system (3.1) with initial value
be any solution of the perturbed system (3.1) with initial value  . By Remark 2.4 we know that
. By Remark 2.4 we know that  is locally Lipschitz in
is locally Lipschitz in  and hence has derivative almost everywhere. Note that at any point
and hence has derivative almost everywhere. Note that at any point  where
where  has derivative we necessarily have
has derivative we necessarily have

Now by Lemma 2.1 we find that

By (2.11) we have

Therefore

Since  , we find that
, we find that

where  are appropriate numbers (which are independent of the initial values). Thus
are appropriate numbers (which are independent of the initial values). Thus

where

and  and
and  are the constants in (2.10). In particular, we have
are the constants in (2.10). In particular, we have

and it follows that

for  , where
, where  .
.
Integrating both sides of (3.12) from  to
to  , one finds that
, one finds that

Since  is locally Lipschitz in
is locally Lipschitz in  , we find that
, we find that

Hence

where  . By the classical Gronwall lemma and (3.15) we obtain
. By the classical Gronwall lemma and (3.15) we obtain

Now for any fixed  we integrate (3.14) from
we integrate (3.14) from  to
to  and find that
and find that

Further integrating the above inequality in  from
from  to
to  , it yields
, it yields

where  . By (2.10) one concludes that
. By (2.10) one concludes that

where  , and
, and  .
.
We also deduce by (2.10) and (3.15) that

Therefore, (3.22) and (3.23) complete the proof of what we desired.
As a direct consequence of Theorem 3.1, we have the following interesting result.
Corollary 3.3.
Assume that  satisfies (F1) and the following sublinear growth condition
satisfies (F1) and the following sublinear growth condition

where  , and
, and  is as in
is as in  .
.
Then system (1.1) is necessarily not uniformly exponentially dissipative.
Proof.
Suppose that (1.1) is uniformly exponentially dissipative. Then by Theorem 3.1, the perturbed system (3.1) is uniformly exponentially dissipative for any perturbation  , provided
, provided  is satisfied with
is satisfied with  sufficiently small. On the other hand, taking
sufficiently small. On the other hand, taking  for any
for any  , by sublinear growth condition on
, by sublinear growth condition on  one easily examine by using standard argument that the perturbed system
one easily examine by using standard argument that the perturbed system

is not dissipative. This leads to a contradiction and proves the conclusion.
3.2. The Cohen-Grossberg Neural Networks with Unbounded External Inputs and Disturbances
As another simple example of the application of Theorem 2.3, we consider the following Cohen-Grossberg neural networks with variable coefficients and multiple delays considered recently in [9]:

where  denote outside inputs and disturbances,
denote outside inputs and disturbances,  , and
, and

denote time delays, where  . For the physical meaning of the coefficients we refer the reader to [9], and so forth. In case
. For the physical meaning of the coefficients we refer the reader to [9], and so forth. In case  is bounded and independent of
is bounded and independent of  , the exponential dissipativity is actually considered in [9]. Here we discuss the more general case. As in [9] we assume that
, the exponential dissipativity is actually considered in [9]. Here we discuss the more general case. As in [9] we assume that
-
(H1)
 are bounded and locally Lipschitz,
are bounded and locally Lipschitz, -
(H2) each function
 belongs to
belongs to 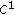 ; moreover,
; moreover, (3.28)
(3.28) -
(H3)
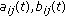 , and
, and 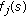 are bounded continuous functions.
are bounded continuous functions.
Theorem 3.4.
Assume (H1)–(H3). Then there exists an  sufficiently small such that for any continuous functions
sufficiently small such that for any continuous functions  satisfying
satisfying

where  is a function as in (3.3), system (3.26) is uniformly exponentially dissipative.
is a function as in (3.3), system (3.26) is uniformly exponentially dissipative.
Proof.
Consider the system

with  . By (H2) one easily verifies that
. By (H2) one easily verifies that  satisfies (F1); moreover, system (3.30) is exponentially dissipative. Let
satisfies (F1); moreover, system (3.30) is exponentially dissipative. Let  be the Lyapunov function of the system given by Theorem 2.3. We show that if
be the Lyapunov function of the system given by Theorem 2.3. We show that if  is sufficiently small, then (3.26) is uniformly exponentially dissipative, provided (3.29) is fulfilled.
is sufficiently small, then (3.26) is uniformly exponentially dissipative, provided (3.29) is fulfilled.
For simplicity we write

where

Then system (3.26) can be reformulated as

where

We observe by (H1), (H3), and (3.29) that

where  , and
, and

Therefore

where  is a constant which only depends on the dimension
is a constant which only depends on the dimension  of the phase space
of the phase space  , and
, and  . Note that the function
. Note that the function

satisfies (3.3) with  therein replaced by another appropriate constant
therein replaced by another appropriate constant  .
.
Now assume that  , where
, where  and
and  are the constants in (2.11) and (2.12). By repeating the same argument as in the proof of Theorem 3.1 with almost no modification, one can show that there exist constants
are the constants in (2.11) and (2.12). By repeating the same argument as in the proof of Theorem 3.1 with almost no modification, one can show that there exist constants  and
and  such that for any solution
such that for any solution  of system (3.26) with initial value
of system (3.26) with initial value

where  , we have
, we have

Here  denotes the usual norm of
denotes the usual norm of  in
in  . We omit the details.
. We omit the details.
The proof of the theorem is complete.
Remark 3.5.
The above result contains Theorem 3.1 in [9] as a particular case.
References
Lyapunov AM: The general problem of the stability of motion. International Journal of Control 1992,55(3):531-534. 10.1080/00207179208934253
Li D, Kloeden PE: Robustness of asymptotic stability to small time delays. Discrete and Continuous Dynamical Systems. Series A 2005,13(4):1007-1034. 10.3934/dcds.2005.13.1007
Yoshizawa T: Stability Theory by Lyapunov's Second Method. The Mathematical Society of Japan, Tokyo, Japan; 1996.
Hale JK: Asymptotic Behavior of Dissipative Systems, Mathematical Surveys and Monographs. Volume 25. American Mathematical Society, Providence, RI, USA; 1988.
Li D: Morse decompositions for general dynamical systems and differential inclusions with applications to control systems. SIAM Journal on Control and Optimization 2007,46(1):35-60. 10.1137/060662101
Robinson JC: Infinite-Dimensional Dynamical Systems, Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge, UK; 2001:xviii+461.
Kloeden PE, Siegmund S: Bifurcations and continuous transitions of attractors in autonomous and nonautonomous systems. International Journal of Bifurcation and Chaos 2005,15(3):743-762. 10.1142/S0218127405012454
Hafstein SF: A constructive converse Lyapunov theorem on exponential stability. Discrete and Continuous Dynamical Systems. Series A 2004,10(3):657-678. 10.3934/dcds.2004.10.657
Jiang M, Shen Y, Liao X: Boundedness and global exponential stability for generalized Cohen-Grossberg neural networks with variable delay. Applied Mathematics and Computation 2006,172(1):379-393. 10.1016/j.amc.2005.02.009
Acknowledgments
The authors highly appreciate the work of the anonymous referees whose comments and suggestions helped them greatly improve the quality of the paper in many aspects. This paper is supported by NNSF of China (10771159).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, X., Guo, Y. A Converse Lyapunov Theorem and Robustness with Respect to Unbounded Perturbations for Exponential Dissipativity. Adv Differ Equ 2010, 726347 (2010). https://doi.org/10.1155/2010/726347
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/726347
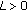 such that
such that
 are bounded and locally Lipschitz,
are bounded and locally Lipschitz, belongs to
belongs to 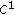 ; moreover,
; moreover,
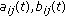 , and
, and 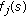 are bounded continuous functions.
are bounded continuous functions.