- Research Article
- Open access
- Published:
Strictly Increasing Solutions of Nonautonomous Difference Equations Arising in Hydrodynamics
Advances in Difference Equations volume 2010, Article number: 714891 (2010)
Abstract
The paper provides conditions sufficient for the existence of strictly increasing solutions of the second-order nonautonomous difference equation  ,
,  , where
, where  is a parameter and
is a parameter and  is Lipschitz continuous and has three real zeros
is Lipschitz continuous and has three real zeros  . In particular we prove that for each sufficiently small
. In particular we prove that for each sufficiently small  there exists a solution
there exists a solution  such that
such that  is increasing,
is increasing,  and
and  . The problem is motivated by some models arising in hydrodynamics.
. The problem is motivated by some models arising in hydrodynamics.
1. Formulation of Problem
We will investigate the following second-order non-autonomous difference equation

where  is supposed to fulfil
is supposed to fulfil



Let us note that  means that for each
means that for each  there exists
there exists  such that
such that  for all
for all  . A simple example of a function
. A simple example of a function  satisfying (1.2)–(1.4) is
satisfying (1.2)–(1.4) is  , where
, where  is a positive constant.
is a positive constant.
A sequence  which satisfies (1.1) is called a solution of (1.1). For each values
which satisfies (1.1) is called a solution of (1.1). For each values  there exists a unique solution
there exists a unique solution  of (1.1) satisfying the initial conditions
of (1.1) satisfying the initial conditions

Then  is called a solution of problem (1.1), (1.5).
is called a solution of problem (1.1), (1.5).
In [1] we have shown that (1.1) is a discretization of differential equations which generalize some models arising in hydrodynamics or in the nonlinear field theory; see [2–6]. Increasing solutions of (1.1), (1.5) with  has a fundamental role in these models. Therefore, in [1], we have described the set of all solutions of problem (1.1), (1.6), where
has a fundamental role in these models. Therefore, in [1], we have described the set of all solutions of problem (1.1), (1.6), where

In this paper, using [1], we will prove that for each sufficiently small  there exists at least one
there exists at least one  such that the corresponding solution of problem (1.1), (1.6) fulfils
such that the corresponding solution of problem (1.1), (1.6) fulfils

Note that an autonomous case of (1.1) was studied in [7]. We would like to point out that recently there has been a huge interest in studying the existence of monotonous and nontrivial solutions of nonlinear difference equations. For papers during last three years see, for example, [8–22]. A lot of other interesting references can be found therein.
2. Four Types of Solutions
Here we present some results of [1] which we need in next sections. In particular, we will use the following definitions and lemmas.
Definition 2.1.
Let  be a solution of problem (1.1), (1.6) such that
be a solution of problem (1.1), (1.6) such that

Then  is called a damped solution.
is called a damped solution.
Definition 2.2.
Let  be a solution of problem (1.1), (1.6) which fulfils
be a solution of problem (1.1), (1.6) which fulfils

Then  is called a homoclinic solution.
is called a homoclinic solution.
Definition 2.3.
Let  be a solution of problem (1.1), (1.6). Assume that there exists
be a solution of problem (1.1), (1.6). Assume that there exists  , such that
, such that  is increasing and
is increasing and

Then  is called an escape solution.
is called an escape solution.
Definition 2.4.
Let  be a solution of problem (1.1), (1.6). Assume that there exists
be a solution of problem (1.1), (1.6). Assume that there exists  ,
,  , such that
, such that  is increasing and
is increasing and

Then  is called a non-monotonous solution.
is called a non-monotonous solution.
Lemma 2.5 (see [1] (on four types of solutions)).
Let  be a solution of problem (1.1), (1.6). Then
be a solution of problem (1.1), (1.6). Then  is just one of the following four types:
is just one of the following four types:
-
(I)
 is an escape solution;
is an escape solution; -
(II)
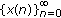 is a homoclinic solution;
is a homoclinic solution; -
(III)
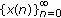 is a damped solution;
is a damped solution; -
(IV)
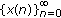 is a non-monotonous solution.
is a non-monotonous solution.
Lemma 2.6 (see [1] (estimates of solutions)).
Let  be a solution of problem (1.1), (1.6). Then there exists a maximal
be a solution of problem (1.1), (1.6). Then there exists a maximal  satisfying
satisfying

Further, if  , then moreover
, then moreover


for  if
if  , and for
, and for  if
if  , where
, where

In [1] we have proved that the set consisting of damped and non-monotonous solutions of problem (1.1), (1.6) is nonempty for each sufficiently small  . This is contained in the next lemma.
. This is contained in the next lemma.
Lemma 2.7 (see [1] (on the existence of non-monotonous or damped solutions)).
Let  , where
, where  is defined by (1.4). There exists
is defined by (1.4). There exists  such that if
such that if  , then the corresponding solution
, then the corresponding solution  of problem (1.1), (1.6) is non-monotonous or damped.
of problem (1.1), (1.6) is non-monotonous or damped.
In Section 4 of this paper we prove that also the set of escape solutions of problem (1.1), (1.6) is nonempty for each sufficiently small  . Note that in our next paper [23] we prove this assertion for the set of homoclinic solutions.
. Note that in our next paper [23] we prove this assertion for the set of homoclinic solutions.
3. Properties of Solutions
Now, we provide other properties of solutions important in the investigation of escape solutions.
Lemma 3.1.
Let  be an escape solution of problem (1.1), (1.6). Then
be an escape solution of problem (1.1), (1.6). Then  is increasing.
is increasing.
Proof.
Due to (1.1),  fulfils
fulfils

According to Definition 2.3 there exists  , such that
, such that  is increasing and (2.3) holds. By (1.3) we get
is increasing and (2.3) holds. By (1.3) we get  . Consequently, by (3.1) and (2.3),
. Consequently, by (3.1) and (2.3),  and
and  . Similarly
. Similarly  and
and

This yields that  is increasing.
is increasing.
Lemma 3.2.
Assume that  for
for  . Choose an arbitrary
. Choose an arbitrary  . Let
. Let  and let
and let  and
and  be a solution of problem (1.1), (1.6) with
be a solution of problem (1.1), (1.6) with  and
and  , respectively. Let
, respectively. Let  be the Lipschitz constant for
be the Lipschitz constant for  on
on  . Then
. Then


where  ,
,  .
.
Proof.
By (3.1) we have

Summing it for  , we get by (1.6)
, we get by (1.6)

Summing it again for  , we get
, we get

and similarly

From this and by using summation by parts we easily obtain

By the discrete analogue of the Gronwall-Bellman inequality (see, e.g., [24, Lemma  ]), we get
]), we get

which yields (3.3).
By (3.6) and (3.3) we have for  ,
,  ,
,

4. Existence of Escape Solutions
Lemma 4.1.
Assume that  and
and  . Let
. Let  be a solution of problem (1.1), (1.6) with
be a solution of problem (1.1), (1.6) with  ,
,  . For
. For  choose a maximal
choose a maximal  such that
such that  for
for  if
if  is finite, and for
is finite, and for  if
if  , and
, and  is increasing if
is increasing if  . Then there exists
. Then there exists  such that for any
such that for any  there exists a unique
there exists a unique  ,
,  , such that
, such that

Moreover, if the sequence  is unbounded, then there exists
is unbounded, then there exists  such that the solution
such that the solution  of problem (1.1), (1.6) with
of problem (1.1), (1.6) with  is an escape solution.
is an escape solution.
Proof.
Choose  such that
such that

For  denote by
denote by  a solution of problem (1.1), (1.6) with
a solution of problem (1.1), (1.6) with  . The existence of
. The existence of  is guaranteed by Lemma 2.6. By Lemma 2.5,
is guaranteed by Lemma 2.6. By Lemma 2.5,  is just one of the types (I)–(IV), and if
is just one of the types (I)–(IV), and if  , then the monotonicity of
, then the monotonicity of  yields a unique
yields a unique  ,
,  , satisfying (4.1).
, satisfying (4.1).
For  , consider the sequence
, consider the sequence  and assume that it is unbounded. Then we have
and assume that it is unbounded. Then we have

(otherwise we take a subsequence.) Assume on the contrary that for any  ,
,  is not an escape solution. Choose
is not an escape solution. Choose  . If
. If  is damped, then by Definition 2.1, we have
is damped, then by Definition 2.1, we have  and
and

If  is homoclinic, then by Definition 2.2, we have
is homoclinic, then by Definition 2.2, we have  and
and

If  is non-monotonous, then by Definition 2.4, we have
is non-monotonous, then by Definition 2.4, we have  and
and

To summarize if  is not an escape solution, then by (4.4), (4.5), and (4.6), we have
is not an escape solution, then by (4.4), (4.5), and (4.6), we have

Since  , there exists
, there exists  satisfying
satisfying

Consider (3.5) with  . By dividing it by
. By dividing it by  , multiplying such obtained equality by
, multiplying such obtained equality by  and summing in
and summing in  from 1 to
from 1 to  we get
we get

Denote

Then we get

Let us put  and
and  to (4.11) and subtract. By (4.7) and (4.8) we get
to (4.11) and subtract. By (4.7) and (4.8) we get

Let us put  and
and  to (4.10) and subtract. We get
to (4.10) and subtract. We get

Choose  and
and  such that
such that

Let  . Then (4.6) holds. Since
. Then (4.6) holds. Since  ,
,  and
and  , (3.1) yields
, (3.1) yields

and hence

Clearly, if  , then by (4.4) and (4.5), inequality (4.16) holds, as well. By (1.2),
, then by (4.4) and (4.5), inequality (4.16) holds, as well. By (1.2),  is integrable on
is integrable on  . So, having in mind (4.1), we can find
. So, having in mind (4.1), we can find  such that if
such that if

then

Therefore, due to (1.3) and (4.7),

Let  be such that
be such that

If  , then (2.7) implies (4.17) and hence (4.19) holds.
, then (2.7) implies (4.17) and hence (4.19) holds.
Now, let us put  and choose
and choose  . Then, (4.2), (4.14), (4.20), and (4.13)–(4.19) yield
. Then, (4.2), (4.14), (4.20), and (4.13)–(4.19) yield

Finally, (4.12) and (4.21) imply

Letting  , we obtain, by (4.3), that
, we obtain, by (4.3), that  , contrary to (4.17). Therefore an escape solution
, contrary to (4.17). Therefore an escape solution  of problem (1.1), (1.6) with
of problem (1.1), (1.6) with  must exist.
must exist.
Now, we are in a position to prove the next main result.
Theorem 4.2 (On the existence of escape solutions).
There exists  such that for any
such that for any  the initial value problem (1.1), (1.6) has an escape solution for some
the initial value problem (1.1), (1.6) has an escape solution for some  .
.
Proof.
We have the following steps.
Step 1.
Let us define

and consider an auxiliary equation

Let  be the constant of Lemma 4.1 for problem (4.24), (1.6). Choose
be the constant of Lemma 4.1 for problem (4.24), (1.6). Choose  ,
,  and let
and let  be the Lipschitz constant for
be the Lipschitz constant for  on
on  . Consider a sequence
. Consider a sequence  such that
such that  . Then, for each
. Then, for each  there exists
there exists  such that
such that

Let  for
for  . Then the sequence
. Then the sequence  is the unique solution of problem (4.24), (1.6) with
is the unique solution of problem (4.24), (1.6) with  . Let
. Let  be a solution of problem (4.24), (1.6) with
be a solution of problem (4.24), (1.6) with  ,
,  , and let
, and let  be the sequence corresponding to
be the sequence corresponding to  by Lemma 4.1. We prove that
by Lemma 4.1. We prove that  is unbounded. According to Lemma 3.2, for each
is unbounded. According to Lemma 3.2, for each  ,
,

Consequently, (4.25) and (4.26) give

and hence

Therefore

which yields that  is unbounded. By Lemma 4.1, the auxiliary initial value problem (4.24), (1.6) has an escape solution for some
is unbounded. By Lemma 4.1, the auxiliary initial value problem (4.24), (1.6) has an escape solution for some  . Denote this solution by
. Denote this solution by  .
.
Step 2.
By Definition 2.3, there exists  such that
such that

Now, consider the solution  of our original problem (1.1), (1.6) with
of our original problem (1.1), (1.6) with  . Due to (4.23),
. Due to (4.23),  for
for  . Using (4.30) and Definition 2.3, we get that
. Using (4.30) and Definition 2.3, we get that  is an escape solution of problem (1.1), (1.6).
is an escape solution of problem (1.1), (1.6).
References
Rachůnek L: On four types of solutions. submitted, http://phoenix.inf.upol.cz/~rachunekl/mathair/rr7.pdf
Berestycki H, Lions P-L, Peletier LA:An ODE approach to the existence of positive solutions for semilinear problems in
 . Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012Derrick GH: Comments on nonlinear wave equations as models for elementary particles. Journal of Mathematical Physics 1964, 5: 1252-1254. 10.1063/1.1704233
Dell'Isola F, Gouin H, Rotoli G: Nucleation of spherical shell-like interfaces by second gradient theory: numerical simulations. European Journal of Mechanics—B/Fluids 1996, 15: 545-568.
Gouin H, Rotoli G: An analytical approximation of density profile and surface tension of microscopic bubbles for Van der Waals fluids. Mechanics Research Communications 1997, 24: 255-260. 10.1016/S0093-6413(97)00022-0
Kitzhofer G, Koch O, Lima P, Weinmüller E: Efficient numerical solution of the density profile equation in hydrodynamics. Journal of Scientific Computing 2007,32(3):411-424. 10.1007/s10915-007-9141-0
Rachůnek L, Rachůnková I: On a homoclinic point of some autonomous second-order difference equation. submitted to Journal of Difference Equations and Applications
Amleh AM, Camouzis E, Ladas G: On second-order rational difference equation. I. Journal of Difference Equations and Applications 2007,13(11):969-1004. 10.1080/10236190701388492
Berenhaut KS, Stević S:The difference equation
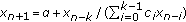 has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088
has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088Berg L:On the asymptotics of the difference equation
 . Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041
. Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041Gutnik L, Stević S: On the behaviour of the solutions of a second-order difference equation. Discrete Dynamics in Nature and Society 2007, 2007:-14.
Hu L-X, Li W-T, Stević S: Global asymptotic stability of a second order rational difference equation. Journal of Difference Equations and Applications 2008,14(8):779-797. 10.1080/10236190701827945
Iričanin B, Stević S: Eventually constant solutions of a rational difference equation. Applied Mathematics and Computation 2009,215(2):854-856. 10.1016/j.amc.2009.05.044
Rachůnková I, Rachůnek L: Singular discrete problem arising in the theory of shallow membrane caps. Journal of Difference Equations and Applications 2008,14(7):747-767. 10.1080/10236190701843371
Rachůnková I, Rachůnek L: Singular discrete and continuous mixed boundary value problems. Mathematical and Computer Modelling 2009,49(3-4):413-422. 10.1016/j.mcm.2008.09.004
Rachůnek L, Rachůnková I: Approximation of differential problems with singularities and time discontinuities. Nonlinear Analysis: Theory, Methods & Applications 2009, 71: e1448-e1460. 10.1016/j.na.2009.01.183
Rouhani BD, Khatibzadeh H: A note on the asymptotic behavior of solutions to a second order difference equation. Journal of Difference Equations and Applications 2008,14(4):429-432. 10.1080/10236190701825162
Stević S: Asymptotics of some classes of higher-order difference equations. Discrete Dynamics in Nature and Society 2007, 2007:-20.
Stević S: Asymptotic periodicity of a higher-order difference equation. Discrete Dynamics in Nature and Society 2007, 2007:-9.
Stević S: Existence of nontrivial solutions of a rational difference equation. Applied Mathematics Letters 2007,20(1):28-31. 10.1016/j.aml.2006.03.002
Stević S: Nontrivial solutions of higher-order rational difference equations. Matematicheskie Zametki 2008,84(5):772-780.
Sun T, Xi H, Quan W: Existence of monotone solutions of a difference equation. Discrete Dynamics in Nature and Society 2008, 2008:-8.
Rachůnek L, Rachůnková I: Homoclinic solutions of non-autonomous difference equations arising in hydrodynamics. in preparation
Elaydi SN: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 2nd edition. Springer, New York, NY, USA; 1999:xviii+427.
Acknowledgments
The paper was supported by the Council of Czech Government MSM 6198959214. The authors thank the referees for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rachůnek, L., Rachůnková, I. Strictly Increasing Solutions of Nonautonomous Difference Equations Arising in Hydrodynamics. Adv Differ Equ 2010, 714891 (2010). https://doi.org/10.1155/2010/714891
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/714891
 is an escape solution;
is an escape solution;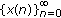 is a homoclinic solution;
is a homoclinic solution;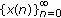 is a damped solution;
is a damped solution;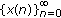 is a non-monotonous solution.
is a non-monotonous solution.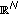 . Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012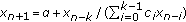 has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088
has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088 . Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041
. Journal of Difference Equations and Applications 2008,14(1):105-108. 10.1080/10236190701503041