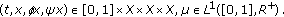- Research Article
- Open access
- Published:
Existence of Solutions for Nonlinear Fractional Integro-Differential Equations with Three-Point Nonlocal Fractional Boundary Conditions
Advances in Difference Equations volume 2010, Article number: 691721 (2010)
Abstract
We prove the existence and uniqueness of solutions for nonlinear integro-differential equations of fractional order  with three-point nonlocal fractional boundary conditions by applying some standard fixed point theorems.
with three-point nonlocal fractional boundary conditions by applying some standard fixed point theorems.
1. Introduction
Fractional calculus (differentiation and integration of arbitrary order) is proved to be an important tool in the modelling of dynamical systems associated with phenomena such as fractal and chaos. In fact, this branch of calculus has found its applications in various disciplines of science and engineering such as mechanics, electricity, chemistry, biology, economics, control theory, signal and image processing, polymer rheology, regular variation in thermodynamics, biophysics, blood flow phenomena, aerodynamics, electro-dynamics of complex medium, viscoelasticity and damping, control theory, wave propagation, percolation, identification, and fitting of experimental data [1–4].
Recently, differential equations of fractional order have been addressed by several researchers with the sphere of study ranging from the theoretical aspects of existence and uniqueness of solutions to the analytic and numerical methods for finding solutions. For some recent work on fractional differential equations, see [5–11] and the references therein.
In this paper, we study the following nonlinear fractional integro-differential equations with three-point nonlocal fractional boundary conditions

where  is the standard Riemann-Liouville fractional derivative,
is the standard Riemann-Liouville fractional derivative,  :
:  is continuous, for
is continuous, for  :
: 

and  satisfies the condition
satisfies the condition  Here,
Here,  is a Banach space and
is a Banach space and  denotes the Banach space of all continuous functions from
denotes the Banach space of all continuous functions from  endowed with a topology of uniform convergence with the norm denoted by
endowed with a topology of uniform convergence with the norm denoted by 
We remark that fractional boundary conditions result in the existence of both electric and magnetic surface currents on the strip and are similar to the impedance boundary conditions with pure imaginary impedance, and in the physical optics approximation, the ratio of the surface currents is the same as for the impedance strip. For the comparison of the physical characteristics of the fractional and impedance strips such as radiation pattern, monostatic radar cross-section, and surface current densities, see [12]. The concept of nonlocal multipoint boundary conditions is quite important in various physical problems of applied nature when the controllers at the end points of the interval (under consideration) dissipate or add energy according to the censors located at intermediate points. Some recent results on nonlocal fractional boundary value problems can be found in [13–15].
2. Preliminaries
Let us recall some basic definitions [1–3] on fractional calculus.
Definition 2.1.
The Riemann-Liouville fractional integral of order  is defined as
is defined as

provided the integral exists.
Definition 2.2.
The Riemann-Liouville fractional derivative of order  for a function
for a function  is defined by
is defined by

provided the right-hand side is pointwise defined on 
Lemma 2.3 (see [16]).
For  let
let  . Then
. Then

where  (
( is the smallest integer such that
is the smallest integer such that  ).
).
Lemma 2.4 (see [2]).
Let  . Then
. Then




Lemma 2.5.
For a given  the unique solution of the boundary value problem
the unique solution of the boundary value problem

is given by

Proof.
In view of Lemma 2.3, the fractional differential equation in (2.4) is equivalent to the integral equation

where  are arbitrary constants. Applying the boundary conditions for (2.4), we find that
are arbitrary constants. Applying the boundary conditions for (2.4), we find that  and
and

Substituting the values of  and
and  in (2.6), we obtain (2.5). This completes the proof.
in (2.6), we obtain (2.5). This completes the proof.
3. Main Results
To establish the main results, we need the following assumptions.
-
(A1) There exist positive functions
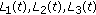 such that
such that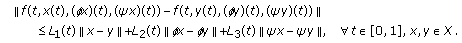 (3.1)
(3.1)Further,
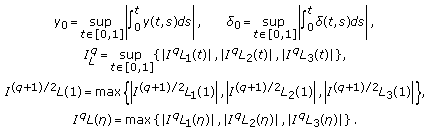 (3.2)
(3.2) -
(A2) There exists a number
 such that
such that 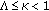 , where
, where (3.3)
(3.3) -
(A3)
 for all
for all 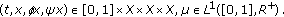
Theorem 3.1.
Assume that  is a jointly continuous function and satisfies the assumption
is a jointly continuous function and satisfies the assumption  Then the boundary value problem (1.1) has a unique solution provided
Then the boundary value problem (1.1) has a unique solution provided  , where
, where  is given in the assumption
is given in the assumption  .
.
Proof.
Define  by
by

Let us set  and choose
and choose

where  is such that
is such that  Now we show that
Now we show that  where
where  For
For  we have
we have

Now, for  and for each
and for each  we obtain
we obtain

where we have used the assumption  . As
. As  therefore
therefore  is a contraction. Thus, the conclusion of the theorem follows by the contraction mapping principle.
is a contraction. Thus, the conclusion of the theorem follows by the contraction mapping principle.
Now, we state Krasnoselskii's fixed point theorem [17] which is needed to prove the following result to prove the existence of at least one solution of (1.1).
Theorem 3.2.
Let  be a closed convex and nonempty subset of a Banach space
be a closed convex and nonempty subset of a Banach space  Let
Let  be the operators such that (i)
be the operators such that (i) whenever
whenever  ; (ii)
; (ii) is compact and continuous; (iii)
is compact and continuous; (iii) is a contraction mapping. Then there exists
is a contraction mapping. Then there exists  such that
such that 
Theorem 3.3.
Let  be jointly continuous, and the assumptions
be jointly continuous, and the assumptions  and
and  hold with
hold with

Then there exists at least one solution of the boundary value problem (1.1) on 
Proof.
Let us fix

and consider  We define the operators
We define the operators  and
and  on
on  as
as

For  we find that
we find that

Thus,  It follows from the assumption
It follows from the assumption  that
that  is a contraction mapping for
is a contraction mapping for 
In order to prove that  is compact and continuous, we follow the approach used in [6, 7]. Continuity of
is compact and continuous, we follow the approach used in [6, 7]. Continuity of  implies that the operator
implies that the operator  is continuous. Also,
is continuous. Also,  is uniformly bounded on
is uniformly bounded on  as
as

Now, we show that  is equicontinuous. Since
is equicontinuous. Since  is bounded on the compact set
is bounded on the compact set  , therefore, we define
, therefore, we define  . Consequently, for
. Consequently, for  , we have
, we have

which is independent of  So,
So,  is relatively compact on
is relatively compact on  . Hence, By Arzela-Ascoli's Theorem,
. Hence, By Arzela-Ascoli's Theorem,  is compact on
is compact on  . Thus all the assumptions of Theorem 3.2 are satisfied and the conclusion of Theorem 3.2 implies that the boundary value problem (1.1) has at least one solution on
. Thus all the assumptions of Theorem 3.2 are satisfied and the conclusion of Theorem 3.2 implies that the boundary value problem (1.1) has at least one solution on 
Example 3.
Consider the following boundary value problem:

Here,  With
With  we find that
we find that

Thus, by Theorem 3.1, the boundary value problem (3.14) has a unique solution on 
4. Conclusions
This paper studies the existence and uniqueness of solutions for nonlinear integro-differential equations of fractional order  with three-point nonlocal fractional boundary conditions involving the fractional derivative
with three-point nonlocal fractional boundary conditions involving the fractional derivative  . Our results are based on a generalized variant of Lipschitz condition given in
. Our results are based on a generalized variant of Lipschitz condition given in  , that is, there exist positive functions
, that is, there exist positive functions  and
and  such that
such that

In case  , and
, and  are constant functions, that is,
are constant functions, that is,  , and
, and  (
( and
and  are positive real numbers), then Lipschitz-generalized variant reduces to the classical Lipschitz condition and
are positive real numbers), then Lipschitz-generalized variant reduces to the classical Lipschitz condition and  in the assumption
in the assumption  takes the form
takes the form

In the limit  , our results correspond to a second-order integro-differential equation with fractional boundary conditions:
, our results correspond to a second-order integro-differential equation with fractional boundary conditions:

References
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Gordon and Breach Science, Yverdon, Switzerland; 1993:xxxvi+976.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Sabatier J, Agrawal OP, Machad JAT (Eds): Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering. Springer, Dordrecht, The Netherlands; 2007:xiv+552.
Daftardar-Gejji V, Bhalekar S: Boundary value problems for multi-term fractional differential equations. Journal of Mathematical Analysis and Applications 2008,345(2):754-765. 10.1016/j.jmaa.2008.04.065
N'Guérékata GM: A Cauchy problem for some fractional abstract differential equation with non local conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1873-1876. 10.1016/j.na.2008.02.087
Mophou GM, N'Guérékata GM: On integral solutions of some nonlocal fractional differential equations with nondense domain. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4668-4675. 10.1016/j.na.2009.03.029
Lakshmikantham V, Leela S, Devi JV: Theory of Fractional Dynamic Systems. Cambridge Academic Publishers, Cambridge, UK; 2009.
Gafiychuk V, Datsko B: Mathematical modeling of different types of instabilities in time fractional reaction-diffusion systems. Computers & Mathematics with Applications 2010,59(3):1101-1107. 10.1016/j.camwa.2009.05.013
Mophou GM: Existence and uniqueness of mild solutions to impulsive fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3-4):1604-1615. 10.1016/j.na.2009.08.046
Ahmad B: Existence of solutions for irregular boundary value problems of nonlinear fractional differential equations. Applied Mathematics Letters 2010,23(4):390-394. 10.1016/j.aml.2009.11.004
Veliev EI, Ivakhnychenko MV, Ahmedov TM: scattering properties of the strip with fractional boundary conditions and comparison with the impedance strip. Progress In Electromagnetics Research C 2008, 2: 189-205.
Ahmad B, Nieto JJ: Existence of solutions for nonlocal boundary value problems of higher-order nonlinear fractional differential equations. Abstract and Applied Analysis 2009, 2009:-9.
Ahmad B, Graef JR: Coupled systems of nonlinear fractional differential equations with nonlocal boundary conditions. PanAmerican Mathematical Journal 2009,19(3):29-39.
Ahmad B, Nieto JJ: Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions. Computers & Mathematics with Applicationsl 2009,58(9):1838-1843. 10.1016/j.camwa.2009.07.091
Bai Z, Lü H: Positive solutions for boundary value problem of nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2005,311(2):495-505. 10.1016/j.jmaa.2005.02.052
Smart DR: Fixed Point Theorems. Cambridge University Press, London, UK; 1980:viii+93.
Acknowledgment
The authors are grateful to the referees for their careful review of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Alsaedi, A., Ahmad, B. Existence of Solutions for Nonlinear Fractional Integro-Differential Equations with Three-Point Nonlocal Fractional Boundary Conditions. Adv Differ Equ 2010, 691721 (2010). https://doi.org/10.1155/2010/691721
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/691721
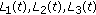 such that
such that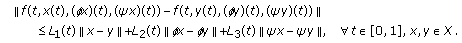
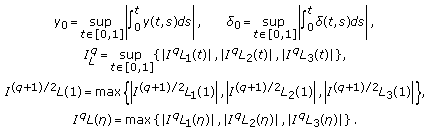
 such that
such that 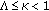 , where
, where
 for all
for all